新的单位是怎样产生的——基于知识本质剖析的度量单位教学思考

文|池红梅

量感，是《义务教育数学课程标准（2022 年版）》中数学学科核心素养的主要表现之一。主要是指对事物的可测量属性及大小关系的直观感知。具体表现有以下几个方面：一是知道度量的意义;二是能够理解统一度量单位的必要性；三是会针对真实情境选择合适的度量单位进行度量，会在同一度量方法下进行不同单位的换算；四是初步感知度量工具和方法引起的误差，能合理得到或估计度量的结果。针对以上表现，我们可以从中抽取几个关于量感认识的关键词“度量意义”“度量单位”“度量方法”“度量工具”“定量描述”。其中，度量单位是在人类漫长的发展过程中，逐步建立和完善起来的度量标准和度量系统。关于度量单位的教学，就成了量感培养的重点。

在小学阶段的数学学习中，度量单位是一个核心概念。但在日常教学中，关于度量单位的教学，特别是涉及数的运算与图形的测量部分，存在一定的认识误区。如“10×10=100”，认为是计数单位“十”乘计数单位“十”产生新的计数单位“百”，如“3 厘米×3 厘米=9平方厘米”，认为是“厘米乘厘米产生平方厘米”，真的是这样吗？

本文拟从以下几方面进行剖析，从而在厘清知识本质的基础上探索出与度量单位有关内容的正确教学路径，从而帮助学生形成量感。

一、单位如何自成体系

单位是指计量事物的标准量的名称。什么是计量事物的标准量呢？因为度量的本质是指用统一的度量单位去测量，看度量对象包含多少个单位，最后为度量对象赋值也就得到了度量的结果。度量包括抽象度量和具象度量，抽象度量是用通过抽象得到的计数单位去测量，如数数、写数、比等；具象度量主要是指利用工具得到的计量单位去刻画事物的重量、长度、能量、体积、温度、速度等。下面我们分别以“计数单位”与“长度单位”为例进行分析。

国际通用的计数单位是以十进制为基础，人类首先将自然数1定义为最基本的计数单位“一”，然后满十进一，将10 个一定义为一1 个十，10 个十定义为1 个百，以此类推。也就是说，从计数单位一到十，并不是由计数单位一相乘得到的，而是由于计数单位一的累加，达到了一个新的标准（十进制下新的标准就是累加达到10个），于是就定义产生了一个新的计数单位“十”。同理，计数单位0.1，是将计数单位一进行十份的细分，将细分后的其中一份（即十分之一）命名为计数单位0.1，而0.01 又是将0.1 细分后命名的其中一份（即百分之一）。

国际通用的长度单位也经历了一个漫长的发展过程。1889 年第一届国际计量大会决定，把长度单位“米”固化，制作出了“米原器”，并以“米”为基本单位。通过十进制，衍生出了现在统一使用的国际度量长度单位体系。先定义了1 米，再将1 米平均分成十份，其中一份命名为分米，再将1分米平均分成十份，其中一份命名为厘米，这是长度单位往小的细分；而长度单位往大的累加，也应该有十米、百米。其实关于十米百米的长度单位，在面积单位里是有专门命名的。如边长为一米的正方形面积是一平方米，边长为一百米的正方形面积为一公顷，边长为一千米的正方形面积为一平方千米。由于省略了“平方十米”的学习，小学阶段的学习是平方米、公顷、平方千米，学生往往记不住它们之间的进率。

长度单位与面积单位的发展结构，如图所示：

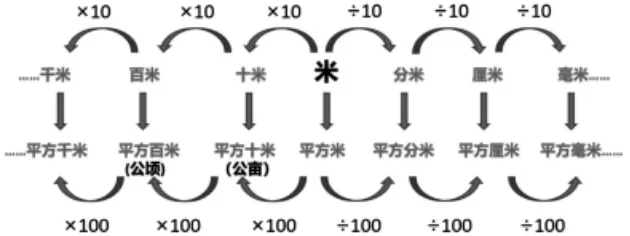
国际通用的七个基本单位为长度m、时间s、质量kg 等，每一个单位体系都在基本单位的基础上通过往大的累加和往细的均分形成自己的单位体系。

二、单位能相互运算吗

1.计数单位能相乘吗？

以40×20 与0.4×0.2 为例，根据相关运算律，可以进行如下运算：

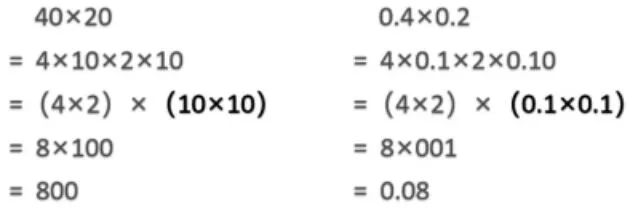
这样的运算，背后的算理是什么呢？我们用几何直观来说理，如图：

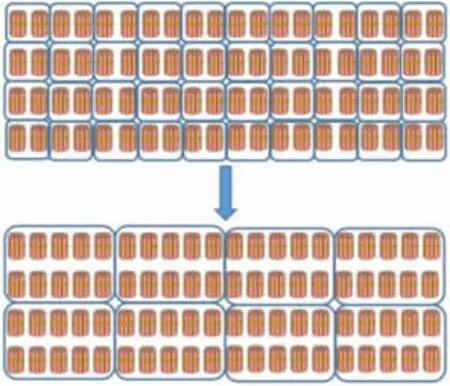
40×20，表示40 个20 相加，可以先将10 个10 打包，累加为一个新的计数单位百，会发现有这样的8 个百。实际上在计算10×10 中两个10 所表示的意义是不一样的。第一个10 作为计数单位十，第二个10 就表示的是计数单位的个数是10 个，10 个十累加为1 个百，并不是计数单位十乘十的结果，而是因为10 个十达到了新的计数单位的标准。

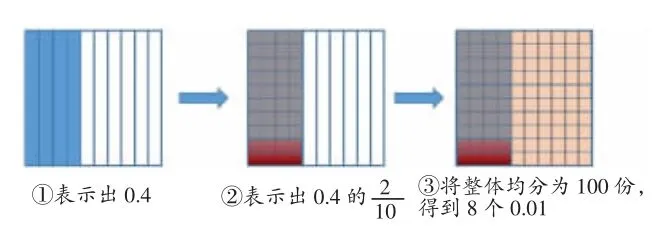
0.4×0.2，首先在图中表示出0.4，根据小数的意义，0.2×0.4 就是求0.4的是多少。把0.4 看作一个整体，将它平均分成10份，取其中的2 份。这时通过图能看到0.4 的0.2 是8 小格，那这个每一小格是多少呢？这时发现如果仅仅将0.4 平均分成10 份，并没有把原来的整体1 平均分成一样的份数，而要将剩下的0.6 都均分成10 份，其实也就是将整体平均分成了100 份，每一份就是0.01。由此可见，0.1×0.1，也并不是两个计数单位0.1 相乘，同理也是一个0.1 表示计数单位，一个0.1表示计数单位的个数，也就是将计数单位再进一步细分成十份，取其中一份，从而产生了新的计数单位。

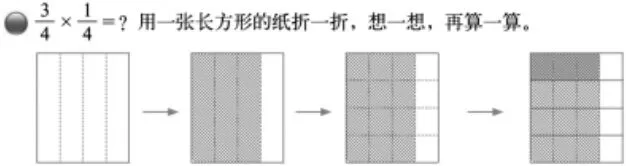
2.长度单位能相乘进而产生面积单位吗？

长方形的面积=长×宽，当一个长方形的长为3 厘米，宽为2厘米时，它能摆下6 个面积为1平方厘米的面积单位，这个“6”得到的过程，就正好是3×2。实际上严格地来讲3×2=6，6 的单位不应该直接带平方厘米，而应该是3×2=6（个平方厘米）。数学上为了表达更加简洁，我们就约定省略掉“个”，于是才有3×2=6（平方厘米）。同上面的计数单位的运算相同，这里的3 和2，所表示的并不是3 厘米和2 厘米的长度，3 代表的是一行可以摆3 个面积为1 平方厘米的面积单位，2 表示可以摆这样的2 行，最后的结果就是3×2=6，6 是计算得到的面积单位的数量。长度单位的变化，是因为所对应的面积单位发生了变化。而面积单位规定了边长为1 厘米的正方形面积就是1 平方厘米。

到体积单位，也是同理可证。我们先定义了棱长为1 厘米的正方体体积为1 立方厘米、棱长为1分米的正方体体积为1 立方分米，然后再计算长方体里包含了多少个这样的体积单位，也就是最后的度量结果。如图：

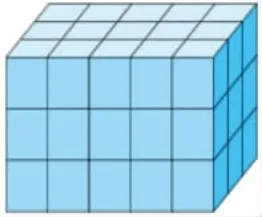
长为5 厘米，宽为3 厘米，高为3 厘米。长乘宽，计算出一层可以摆5×3=15（个立方厘米）；高为3，可以像这样摆3 层，即15×3=45（个立方厘米），也就是5×3×3=45（立方厘米）。因此，长×宽×高，并不是长度乘长度再乘长度就能得到体积单位，而内在的逻辑是先定义了相关的体积单位，再计算出体积单位的个数。

综上所述，无论是计数还是测量，涉及的相关运算，都是在计算已确认的计量单位的个数。

三、如何基于意义的理解开展教学

1.基于运算的一致性，理解运算的法理。

算理就是运算的道理，算法是基于运算的道理而抽象形成的运算方法。基于理解的算法掌握会更利于学生迁移与运用。

整数加减的算法是数位对齐，小数加减的算法是小数点对齐，本质都是相同数位对齐，因为相同计数单位的个数才能相加减。同分母分数加减的算法是分母不变分子相加减，异分母分数的算法是先通分为同分母分数再加减，分母相同是为了保证分数单位相同，再计算分数单位的个数。

整数的乘法是先分别计算有几个一几个十几个百再相加，小数乘法是先按照整数乘法进行计算，再根据乘数的小数位数确定积的小数位数，其实最后确定积的小数位数点上小数点，也就是在确定每一个相应的计数单位的个数。小数除法是在整数除法的基础上，将无法在计数单位一的基础上进行平均分的数细分为更小的计数单位来均分。分数乘法中分母乘分母是根据分数的意义确定新细分的分数单位，分子乘分子是在计算新的分数单位的个数。

整数、小数、分数的四则运算，其本质都是在计算计数单位的个数。理通则法自明，学生能理解了计算背后的道理，所有的运算法则就不再是繁杂的添加，而仅仅是算理一致性这条主干上所生长出的枝杈而已。

2.基于度量的一致性，理解度量的本质。

长度与角度的度量，都是先确定一个统一的标准，然后再利用相应的度量工具（长度的度量工具是直尺，角度的度量工具是量角器），再采用一定的度量方法，最后获得度量结果。面积和体积的度量，没有具体的度量工具，试想生活中我们如何拿着1 平方米的面积工具去铺地呢？又或者如何拿着体积为1 立方米的小方块去堆积？于是聪明的人想到了将二维的度量与三维的度量都转化为利用一维的量去计算出结果。如前文所述，测量出长方形的长和宽，就能计算出能铺满的面积单位的个数；测量出长宽高，就能计算出能堆积的体积单位的个数。在教学面积、体积的内容时，就一定要让学生理解公式所代表的意义。

有了对度量单位本质和体系的认识，学生就能在真实情境中选择合适的度量单位进行度量，并在同一度量方法下进行不同单位的换算，感受单位的换算只是改变度量单位和度量单位的个数，其度量值本身没有变化。

总之，小学阶段关于度量单位的教学，占据了较大篇幅。无论是抽象的计数还是具象的测量，其本质都是计数单位个数的累加与细分的过程，而不是单位乘单位的过程。运算中单位的变化，都是往大乘倍率、往小乘分率的结果。