轮式移动机器人轨迹跟踪控制研究*

张小俊,刘昊学

(河北工业大学机械工程学院，天津 300401)

1 引言

近几年，在控制领域中，移动机器人的理论和应用得到研究人员的广泛关注[1-4]。起初的研究基于运动学模型，控制方法采用线性化反馈控制律，负载变化、参数测量不精确和摩擦等不确定性因素导致机器人不能实现完美的速度跟踪[5]。于是研究人员通过反步法[6]引入动力学模型，将运动学控制器和动力学控制器相结合，解决了上述不确定性问题，但未考虑外界扰动的因素对机器人轨迹跟踪的影响。

文献[7]针对四轮驱动机器人轨迹跟踪，设计反步自适应模糊滑模控制方法，以解决机器人参数不确定性问题。文献[8-10]为减小非完整轮式移动机器人的运动和动态不确定性对轨迹跟踪控制的影响，设计自适应轨迹跟踪控制方法，减小了轨迹跟踪的误差。文献[11]针对非线性不确定系统的外界干扰问题，提出高增益扩张观测器，使得跟踪误差在有外界干扰的情况下也能够迅速收敛。文献[12-14]针对具有扰动的轮式移动机器人跟踪控制问题，设计了扰动观测器和虚拟速度控制律。通过扰动观测器对动态模型的外部扰动进行估计，通过前馈补偿的方式实现精准控制。上述研究的移动机器人轨迹跟踪控制问题，多是根据移动机器人的运动学模型设计跟踪控制器，未考虑动力学模型在受到外界干扰、参数摄动等不确定性因素时对系统稳定性的影响，难以达到预期效果。

因此，本文建立轮式移动机器人的运动学模型和动力学模型，将自适应算法与滑模扩张状态观测器相结合，提出了一种面向轮式移动机器人的基于自适应滑模扩张观测器的轨迹跟踪控制算法，并利用Lyapunov 稳定性理论对系统的稳定性进行分析。其中，自适应虚拟速度控制器用于估计系统的不确定参数;滑模扩张观测器观测外界干扰，消除抖振现象，完成对期望轨迹的精确跟踪任务，且跟踪误差能在有限时间内收敛。最后，利用仿真软件与自适应反演滑模控制算法进行对比，以验证所提算法的有效性和优越性。

2 移动机器人数学模型

2.1 运动学模型的建立

质心和驱动轮轴线中心不重合的六轮移动机器人的基本结构如图1所示。其中，O是机器人对称轴与驱动轮轴线的交点，P是机器人质心，d是O与P的距离，b是驱动轮到对称轴的距离，r是车轮的半径，θ是机器人前进方向与世界坐标系中x轴的夹角。

在作业过程中，具有2个驱动轮的移动机器人无外界干扰的非完整约束方程如式(1)所示:

(1)

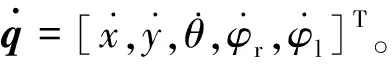
A(q)S(q)=0，

对移动机器人进行运动学分析，可得机器人的线速度v、角速度w与左右车轮速度的关系如式(2)所示：

(2)

进一步可获得机器人位姿与各参数间关系如式(3)所示：

(3)

移动机器人纯滚动的运动学方程如式(4)所示：

(4)

移动机器人在运动过程中经常会出现滑转、滑移等现象,因此不能够满足式(1)的约束条件[15,16]。为解决这类问题，本文将具有滑转、滑移等扰动现象的非完整移动机器人的约束条件表示为式(5)所示:

(5)

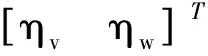
结合机器人纯滚动的运动学方程，可得发生侧滑、滑移等扰动现象的机器人运动学方程如式(6)所示：

(6)

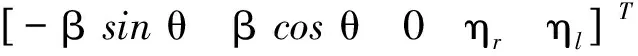
2.2 动力学模型的建立

由移动机器人的力学分析可知，机器人在x,y方向上的受力是平衡的，在电机轴和垂直x-o-y平面方向上的力矩也是平衡的。因此，建立机器人的动力学方程如式(7)所示：

(7)

其中，m表示机器人总质量；FY表示总阻力；Iwh和I分别表示车轮和系统总的转动惯量；FXl和FXr分别表示左、右轮的驱动力。简化式(7)并将其转化成拉格朗日动力学标准状态方程,如式(8)所示[17]：

B(q)τ+(C(q))Tλ

(8)

将拉格朗日动力学标准状态方程两边同时乘以(S(q))T，结合受扰动的运动学方程，可得受扰动的动力学方程,如式(9)所示：

(9)

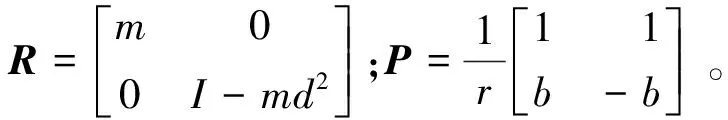
3 机器人轨迹跟踪控制器的设计

基于自适应滑模扩张状态观测器的移动机器人轨迹跟踪控制方案如图2所示。机器人实际位姿与期望位姿之间的误差作为运动学控制器的输入，采用自适应虚拟速度控制器，在线估计不确定性参数并进行调整，保证了位姿误差稳定收敛性。将自适应虚拟速度控制器的虚拟速度与机器人实际速度之间的速度误差作为动力学控制器的输入，利用扩张观测器观测值设计滑模控制器，保证了速度的渐进收敛。针对系统存在的内外部扰动，可通过扩张观测器对其进行在线观测估计并以前馈的方式进行补偿，降低控制器的负担。下面分别介绍设计的自适应速度控制器、扩张状态观测器和滑模控制器。

为达到控制目标，首先作出如下假设：

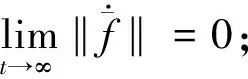
假设2期望的线速度、角速度和其导数均有界。

3.1 自适应虚拟速度控制器

由于机械磨损、质心与几何中心测量误差等原因，机器人质心与几何中心的距离d往往是不精确的[18]。因此，本文采用自适应控制方法设计轨迹跟踪控制器，在线估计未知参数d,使轨迹误差渐进收敛到零。

(10)

机器人的位姿误差微分方程如式(11)所示：

(11)

定义Lyapunov函数V0如式(13)所示：

V0=[(xe+d(1-cosθe))2+(ye-dsinθe)2+

(12)

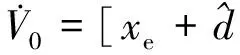
(13)

由Lyapunov函数设计自适应虚拟速度控制器，如式(14)所示：

(14)

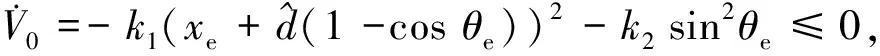
3.2 扩张状态观测器和滑模控制器

自适应虚拟速度控制器能够使机器人的运动学系统按照任意期望速度运行并估计机器人本体的不确定性参数，而机器人的实际速度是靠电机获得的，无法直接获得期望的速度，同时不可避免地存在外部扰动。为解决这个问题，本文将扩张状态观测器与滑模控制器相结合，设计基于扩张状态观测器的滑模控制器。利用扩张观测器观测未知干扰与系统状态变量并将观测值反馈给滑模控制器，对机器人不确定性参数和扰动在线估计和反馈抑制，保证实际速度渐进收敛到虚拟速度[19]。

假设机器人非线性系统的状态方程如式(15)所示：

(15)

其中，f(t)包含不确定性项和外部扰动项，A、B和C为非零矩阵，bm为非零常数。

联合式(9)和式(15)，可获得机器人非线性系统状态方程为如式(16)所示：

(16)

速度扩张观测器和角速度扩张观测器如式(17)所示:

(17)

然后，利用系统的实际输出和期望输出定义系统的跟踪误差e，将滑模面函数表示为式(18):

(18)

其中，c1>0,c2>0,e1=x1-x1r,e2=x3-x3r,x1r和x3r分别为期望位姿中的第1个和第3个分量。

根据滑模函数与扩张观测器设计的控制系统驱动力矩方程如式(19)所示:

(19)

4 稳定性分析

4.1 扩张状态观测器稳定性分析

(20)

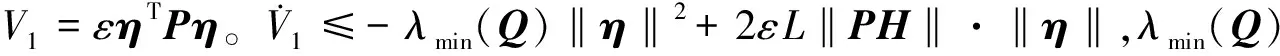
4.2 滑模控制器稳定性分析

(21)

(22)

□

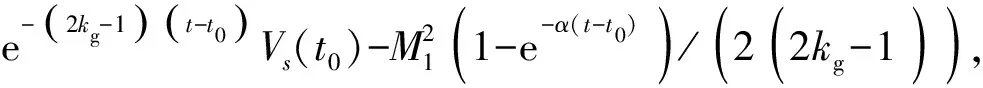
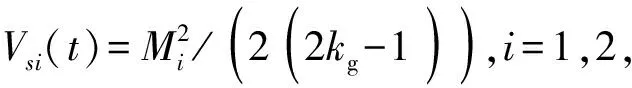
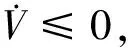
5 仿真分析

(1)圆-直线轨迹跟踪曲线如图3所示，由图3a可知，机器人能够快速平缓地跟踪上圆轨迹，并从圆轨迹平滑地过渡到直线轨迹，不受外界的扰动。由图3b可知，机器人不能在短时间到达预期的轨迹，在圆轨迹到直线轨迹切换时，机器人易受外界的影响，不能迅速恢复预期轨迹。

(2)轨迹跟踪误差曲线如图4所示，2种算法最终都能实现轨迹跟踪误差的渐进收敛。本文所提算法相比传统算法稳定性更好，收敛时间更短。尤其在15 s轨迹切换时，自适应滑模扩张观测算法能够更平稳迅速地收敛。

(3)线速度收敛曲线如图5所示，初始时2种算法的速度变化都很大，但是自适应滑模扩张观测器算法最终都能收敛到期望的速度。自适应反演滑模算法易受扰动的影响，在期望速度上来回波动，在轨迹切换时速度波动更大。

(4)驱动力矩收敛曲线如图6所示，自适应反演滑模算法不能消除滑模控制中的抖振现象，本文所提算法能够有效地消除抖振现象，减小外界扰动对控制的影响。

(5)扰动曲线如图7所示，从图7中可以看出，自适应反演滑模算法不能准确观测扰动现象，自适应滑模扩张观测器控制算法能够在短时间内准确观测扰动。

6 结束语

本文提出的基于自适应滑模扩张观测器轨迹跟踪控制算法能够减小参数摄动和扰动等不确定性因素对移动机器人轨迹跟踪控制精度的影响。将自适应控制律与扩张观测器滑模控制器相结合用在移动机器人的轨迹跟踪控制中，解决了机器人轨迹跟踪控制精度低、稳定性差的难题。本文利用Lyapunov函数证明了控制系统的稳定收敛性；通过仿真软件验证自适应虚拟速度控制器能够调节机器人本体不确定性参数，使得轨迹跟踪误差快速收敛；扩张观测器可以准确观测系统的扰动和参数摄动，与滑模控制器结合使用能抑制扰动。通过与自适应反演滑模控制算法对比分析可知，新型轨迹跟踪控制算法的稳定性和收敛性优于传统控制算法。