基于ARM架构的中值滤波算法优化*
2022-10-28牟明任贾海鹏张云泉邓明森曲国远魏大洲张广婷
牟明任,贾海鹏,张云泉,邓明森,曲国远,魏大洲,张广婷
(1.贵州财经大学信息学院,贵州 贵阳 550025;2.中国科学院计算技术研究所计算机体系结构国家重点实验室,北京 100190;3.中国航空无线电电子研究所,上海 200241)
1 引言
在图像处理中,降低椒盐噪声的常用方法是中值滤波[1,2]。中值滤波是一种基于统计学的非线性滤波技术,图像的噪声值被中值滤波窗口内的中值所代替。中值滤波窗口遍历整幅图像,计算滤波窗口内所有值的中值作为新的像素值。中值滤波算法的中值计算公式如式(1)所示:
g(x,y)=median{f(x-i,y-i),i,j∈H×W}
(1)
其中,f(x,y)和g(x,y)分别是初始图像的值和输出图像的替代值,H×W是滤波窗口的大小(通常H=W且为奇数,比如3×3,5×5,7×7…等)。
对于中值滤波的研究已经有很多,但是目前中值滤波算法仍存在一些问题。基于统计直方图的中值滤波算法虽然在8u的灰度图像的大滤波窗口下执行效率较高,但在小滤波窗口下并不适用,且只局限于在灰度图像上使用。另一方面,针对非8u数据类型的大滤波窗口的中值滤波问题,目前还没有很好的解决算法。
另外,在图像处理问题上,SIMD(Single Instruction Multiple Data)指令是非常适用的,可以显著提高图像处理性能。然而之前的相关工作中并没有充分利用这一并行方式。
本文针对不同数据类型以及不同规模滤波窗口下的自适应中值滤波算法,根据不同的算法提出了不同的优化策略。对于能够并行的算法,本文使用ARM NEON指令集(ARM架构下的矢量寄存器可以以指令流水线的方式高效执行这些数据)进行SIMD实现,进一步提高图像处理性能。
实验结果表明,本文实现的HMPP算法库中的中值滤波自适应算法带来了较好的性能提升,相比于OpenCV的中值滤波算法,性能提升达到120%。
本文的主要贡献如下:
(1)提出了中值滤波自适应算法,针对不同的滤波窗口大小及不同数据类型提出了相对应的算法,提高了中值滤波的效率。
(2)设计了一种针对ARMv8架构的优化策略,使用ARM NEON指令集进行优化,也可对其他算法在ARM处理器上的优化提供参考。
(3)实现了中值滤波算法,并与OpenCV进行了性能比较,且性能更好。
2 相关工作
现在已有较多关于中值滤波算法的研究工作[3-11],基于分治策略的快速算法[5,6]将传统中值滤波算法的时间复杂度从O(scale2)降低到O(scalelogscale)(其中scale表示图像规模);对于8u数据类型的图像来说,文献[7]提出的算法基于可修改的直方图——统计直方图,有效地提升了中值滤波的效率。
在8u的图像中,r,g和b的取值在0~255,那么就可以采用统计方式来计算滤波窗口内的中值,直方图的数组长度为256,数组下标0~255的值为0~255。使用可滑动的滤波窗口,改变窗口内的像素值,滑动求取中值。一个像素的直方图在窗口第一次运行时被设置,从一个位置滑动到下一个位置时,窗口内的值会改变,直到滤波窗口遍历完整幅图像。窗口的中值是通过使用更新的直方图调整前一个窗口的中值来找到的。
对于处理灰度图(8u数据类型),当滤波窗口的半径非常大时,使用直方图算法是十分有效的,算法复杂度为O(scale),且不会随着滤波半径的大小变化产生太大的性能波动。
之后研究人员又提出了一系列基于直方图的改进算法。Perreault等[9]提出的改进算法,提高了中值滤波的效率,但是直方图具有局限性,只能用于数据类型为8u的灰度图像,对于具有更高位数的数据类型(16u,16s,32f,64f)的图像来说,使用直方图求取中值会产生巨大的内存开销。以16u为例,一幅图像中各个点的像素值在0~216,如果使用直方图进行中值滤波,空间开销极大,实现起来是不现实的,同时对于较小滤波窗口来说性能不佳。文献[10]提出的算法中,将中值滤波与均值滤波相结合,能更好地抑制噪声,保留图像细节。引入依旧适用的统计直方图来提高中值的搜索速度,充分利用了图像的相关性。因此,改进算法的复杂度降低到了O(scale)。该算法的性能还取决于用于表示数据值的数据类型,在数据类型变化时,比较的规模以指数级增长。
3 自适应中值滤波算法
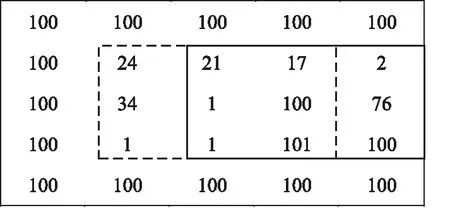
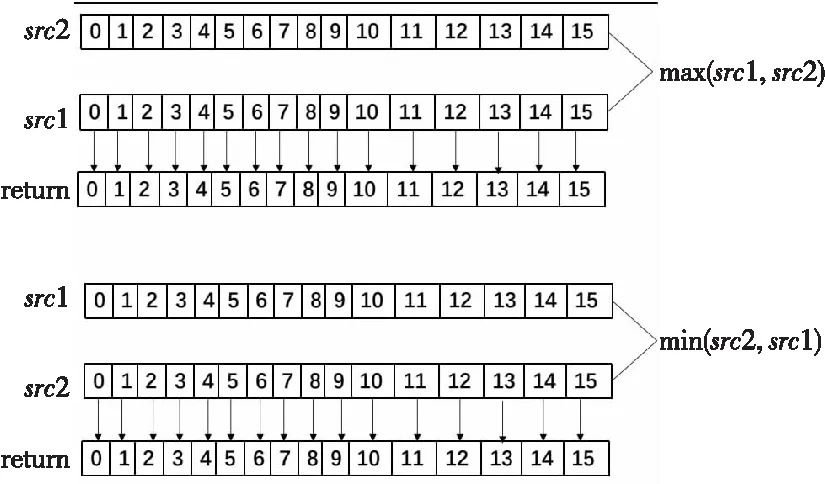
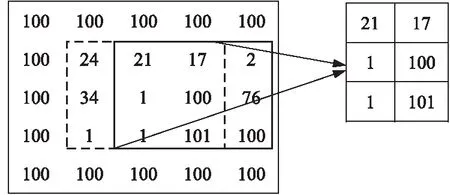
给定一个M×N大小的图像,一个H×W(H Figure 1 Finding the median value in the filtering window 由于中值滤波是一种非线性滤波,对于含有随机噪声的图像,其数学分析较为复杂,对于均值滤波噪声为零的正态分布图像,中值滤波的噪声方差[11]近似如式(2)所示: (2) (3) 比较式(2)和式(3),中值滤波的性能依赖于滤波窗口的大小,同时由于图像数据类型的不同,单一的算法并不能解决所有的问题,因此本文提出了自适应中值滤波算法,根据滤波窗口的大小和数据类型选择最佳算法。 当滤波窗口较小时,即滤波窗口为3×3或5×5时,本文提出了一种单独处理的算法。以3×3滤波窗口为例(H=3,W=3),设滤波窗口内的像素值分别为P0、P1、P2、P3、P4、P5、P6、P7和P8。 本文使用归并排序(Mergesort)的分组思想来优化算法。归并排序算法首先将输入序列分成若干个组,进行组内排序;然后对这些已排序的子序列再次分组,同组内的各有序序列归并为一个有序序列,重复这个过程直到所有组合并为一个有序序列时算法结束。对于一个3×3的窗口,采用严格意义上的归并算法得到中值需要11个时钟周期。而此时所有数据均已排序,由于中值滤波只需找到中间值即可,因此不需要那么多次比较。首先,对每一行的3个像素进行排序,如图2a所示,实现行方向的有序排序;然后将3组有序序列按其列有序进行排序,如图2b所示。在最小值数据组中,1和2不可能是中值,因为窗口中至少有5个数据比它们大;在最大值数据组中,8和9不可能是中值,因为窗口中至少有5个数据比它们小;在中值数据组中,有4个以上的数据不能确定比它们大或者小,这样3、4、5、6、7这5个数中的中间值就是最后窗口的中值。5个元素求中值需要6次比较,但是4、5、6已经有序,故节省了2次比较,可知最终通过16次比较就可以找到中值元素。如图3c所示,取出有序序列组中的最小值中的最大值、最大值中的最小值和中间列的中值,3个数进行比较,就可得到中值。该算法的操作步骤见图2,P0~P8分别代表3×3滤波窗口内的像素值,2个像素之间横线下面的数字代表执行步骤。 Figure 2 Schematic diagram of median algorithm based on 3×3 filtering window 以图2a中第①步的P1和P2为例,首先进行2个像素值的比较,当P1>P2时,P1和P2的像素值需要互换,否则继续进行下一组像素值的比较。当滤波窗口大小为5×5时,算法步骤与3×3算法的一致。该算法可以应用于所有数据类型的3×3和5×5滤波窗口的中值滤波,算法复杂度为O(scale),同时可以通过ARM NEON指令集进行SIMD加速。 当图像为8u的灰度图像时,min(W,H)≥7或者W≠H,本文会采用改进的直方图算法进行中值滤波。 算法具体步骤如下:首先,构建初始直方图,对于灰度图像来说,像素的取值在0~255,设置一个数组,数组长度为256,从原始图像数据(src)中获取滤波窗口内的像素值,构建直方图,获取第一次滤波窗口内的像素值,对应的数组下标内的值加1,直到滤波窗口内的所有像素值全部放入数组内;然后,针对滤波窗口的大小设置阈值T=[(W×H)/2],依次累加数组内包含滤波窗口区域的值对应下标的个数sum,若sum≥T,就说明当前灰度层级的值为所需要的中值,同时滤波窗口向右滑动,依次采取上述方式进行滤波,遍历整幅图像。如图3所示,虚线框与实线框内分别是前后2次滤波窗口内的数据。 Figure 3 Median filtering schematic diagram based on histogram 在数据类型的位数更多(16u,16s,32f,64f)的图像中,直方图根本无法使用,因此针对位数更多的图像,要采取更加适合的算法,本文提出了快速中值算法(Fast Median Algorithm),如算法1所示。 算法1快速中值算法 输入:滤波窗口内所有的像素值。 输出:所求得的中值。 步骤1获取数列长度length=H×W,设有集合p(i),i∈{0,1,2,…,length-2,length-1}。 步骤2分别获取i=0,(length-1)/2,length-1时的p(i)值,比较3个位置像数值的大小,最大值放在i=length-1,最小值放在i=(length-1)/2,i=0位置的像素值为哨兵,将i=1与i=(length-1)/2位置上的像素值互换。 步骤3通过与哨兵的像素值进行比较,确定最终i=m的位置,使得p(left) 步骤4比较m与(length-1)/2的大小,如果m<(length-1)/2,更新数列为m~(length-1);如果m>(length-1)/2,更新数列为1~m,继续执行步骤1~步骤4。 本文根据滤波窗口的大小采取最优的算法后,会使用ARM NEON指令进行SIMD优化。虽然编译器在程序运行时会自动进行优化,但是根据研究发现[12],使用ARM NEON指令集进行手动优化,可以获得更大的加速空间。在图像处理中,使用SIMD可以发挥出更大的性能优势,在ARM处理器中,寄存器被视为统一数据类型的元素的矢量,ARM的矢量寄存器拥有128位,向量寄存器分别可以设置为8,16,32和64宽度的位宽。以8u图像为例,对于1个矢量寄存器1次可以存储16个数据。 对于3×3,5×5滤波窗口的中值滤波来说,本文已经通过3.1节的算法来降低时间复杂度,并且该算法可以使用ARM NEON指令进行优化。 单通道8u的灰度图像的优化策略为:寄存器可以1次并行处理16个数据,意味着寄存器可以从原来1条指令比较2个数到现在1条 指令可以操作2个寄存器中的32个数据相比较一次性得出16个结果。首先使用vld1q_u8()将数据读入矢量寄存器中。由于本文需要频繁地比较数据大小,因此要使用vmin_u8()与vmax_u8()这2条指令,其中vmin_u8()是将2个数据中小的数据存入目标寄存器,vmax_u8()是将2个数据中大的数据存入目标寄存器,2条指令执行的操作都是对2组16个数据进行大小比较,并将结果存入到目标寄存器中。使用这2条指令按照3.1节提出的算法进行操作,最终执行1次可以得到16个中值,如图4所示。 Figure 4 Register storage and operation for grayscale image 当8u的灰度图像为多通道时,优化的难点在于,单通道是由r,g和b这3个像素中的一个决定的,有(r,r,r,…,r,r,r),(g,g,g,…,g,g,g),(b,b,b,…,b,b,b)3种形式,像素间没有数据性依赖且连续,因此在滤波窗口滑动取值时比较容易读入寄存器。 由于多通道灰度图像由(r,g,b,…,r,g,b)或(r,g,b,a,…,r,g,b,a)组成,以第1个元素r为例,首先读取第1个位置i,第2个位置为i+3。如果不采用矢量寄存器进行并行优化,该取数问题非常好解决,只需要控制数组下标即可,但是矢量寄存器读入的数据是连续的,因此本文需要使数据按照需求读入。 因此,本文提出以下优化策略:以8u图像3通道为例,首先使用memcpy()函数将48个384位的r,g,b数据读入内存中,r,g,b数量各为16个,但一个矢量寄存器的位数为128,那么本文需要3个这样的矢量寄存器;使用vld3q_u8()代替uint8x16_tvld1q_u8(),将3组128位的数据依次读入寄存器,这样就会得到连续的r,g和b,并将其分别存储在3个矢量寄存器中。 如图5所示,本文通过多次使用vmin_u8()和vmax_u8()函数进行中值运算。求取中值之后采用vstd3q_u8()函数依次将数据存入目的图像位置。该优化策略采用SIMD进行加速,理论上可以将性能提升16倍。同时,由于本文采取的算法将时间复杂度由原来的O(scale2)降低为O(scale),能很大幅度地提升小滤波窗口中值算法性能。本文在处理大规模数据时,性能十分稳定,在工程中具有较高的实用价值。 Figure 5 Multichannel register storage 对于8u灰度图min(W,H)>5且W≠H时,本文使用基于直方图的中值滤波算法进行处理。在使用直方图进行中值运算时,因为滤波窗口是以滑动的方式进行滤波,会有大量的数据被多次使用。本文在构建直方图的数组时,会剔除垃圾数据,将新数据写入数组中,但这样会增加数据的复用性,以3×3滤波窗口为例,2个相邻数据进行图像滤波时,当前一个位置滤波后,滤波窗口滑动到后一个位置,会产生6个重复数据,如图6所示。如果对大规模数据进行处理,如果数据的复用性不强,会造成资源的浪费,同时也会降低中值滤波算法的性能。根据本文分析,当滤波窗口从前一个位置滑动到后一个位置时,只需对直方图进行一列加操作和一列减操作。如图6所示,虚线窗口为前一个位置像素构成的滤波窗口,实线为后一个位置像素构成的滤波窗口。该算法的执行步骤如算法2所示。该算法可以增强数据的复用性,缩短数据读取的时间,有效地减少运算量。该算法的优势在于,当滤波窗口尺寸设置得很大时,该算法的滤波时间不会有很大的增加。 Figure 6 Median filtering optimization based on histogram 算法2基于直方图的中值滤波算法 输入:大小为M×N的图像X,滤波窗口radio。 输出:与图像X大小相同的图像Y。 //初始化直方图H //i,j分别为图像X数组的横纵坐标索引 //k表示滤波半径内像素的索引 1:fori=1 toMdo 2:forj=1 toNdo 3:fork=-radiotoradiodo 4: RemoveXi+k,j-radio-1fromH;/*移除左边一列*/ 5: AddXi+k,j+radiotoH;//增加右边一列 6:endfor 7:Yi,j←(median(H);/*median()函数对处理好的直方图进行寻找中值的操作*/ 8:endfor 9:endfor 当更新直方图时,减掉当前滤波窗口的左侧一列,加上当前窗口的右侧一列,解决了数据重复使用的问题,开始对数据比较进行优化。更新完的新直方图中,sum的值与T的关系有3种:当sum=T时,其中值维持不变;当sum>T时,说明中值在当前直方图灰度层级的左边;当sum 算法3基于改进直方图的中值滤波算法 输入:大小为M×N的图像X,滤波窗口radio。 输出:与图像X大小相同的图像Y。 //初始化直方图H //i,j分别为图像X数组的横纵坐标索引 //k表示滤波半径内像素的索引 1:fori=1 toMdo 2:forj=1 toNdo 3:fork=-radiotoradiodo 4: RemoveXi+k,j-radio-1fromH;/*移除左边一列*/ 5: AddXi+k,j+radiotoH;/*增加右边一列*/ /*新的中值在直方图的左侧,其中sum为上一次统计直方图元素个数的和,T表示阈值*/ //判断新的中值在直方图的左侧 6:sum>T /*median()函数对处理好的直方图进行寻找中值的操作*/ 7:Yi,j←median(H); /*判断新的中值在直方图的右侧*/ 8:sum 9:Yi,j←median(H); /*判断新的中值是否位置不变*/ 10:sum=T 11:Yi,j←median(H); 12:endfor 13:endfor 14:endfor 本文讨论的所有算法都是在华为鲲鹏920服务器实验环境上运行的,具体实验环境配置如表1所示。 Table 1 Experimental environment configuration 使用C语言与ARM NEON指令集混合编程,具有良好的跨平台性和可移植性,以下对HMPP库的中值滤波与OpenCV的中值滤波进行性能比对分析。 本文对HMPP库中不同的数据类型及不同的滤波窗口采用了自适应的中值滤波优化算法,其中针对小滤波窗口(3×3,5×5)的中值滤波算法优化适用所有的数据类型。图7是在8u数据类型不同像素规模下对各算法性能进行比较的结果。后面所有性能图中,Hmpp代表本文使用的算法,OpenCV代表对比库OpenCV中相对应的算法。 图7的结果表明,对于本文提出的自适应算法,对于3×3的小滤波半径窗口,算法的最高性能达到OpenCV中值滤波算法的257%,最低为104%,对于1024×1024这种大规模图像,性能提升达到了140%;同时对于该算法来说,除了可以处理灰度图像,还可以处理其他数据类型的图像,应用范围广,具有较高的实用价值。 Figure 7 Performance diagram of different filtering window sizes 该算法最大的创新点在于使用ARM NEON指令集进行优化,且使用了SIMD指令,算法性能提升幅度较大,达到了预期效果。对于5×5滤波窗口,HMPP库使用的中值滤波算法的最高性能相比于OpenCV的提升了377%,最低为115%,相比于OpenCV有较大的性能提升,对于1024×1024这种大规模图像性能提升达到了170%。 实验结果表明,在5×5滤波窗口下,使用该算法及ARM NEON指令集优化后,相对于小滤波窗口的中值滤波,对于OpenCV具有明显的性能优势,整体性能大约为OpenCV的140%。 对于7×7滤波窗口,本文提出的算法性能最高达到了OpenCV的115%,最低达到了114%,针对1024×1024这种大规模图像,性能达到了115%。可以看出,改进的直方图性能提升明显,同时性能不会随着图像规模的增大有明显的波动,性能提升基本维持在115%。实验结果表明,使用该算法能带来稳定的性能提升。 对于11×11滤波窗口,从图7中可以看到,本文提出的算法性能最高达到OpenCV的130%,最低达到了110%,针对1024×1024这种大规模图像,性能达到了110%。实验结果表明,在滤波窗口不断增大时,该算法对性能不会有太大的影响。可以看出,基于直方图的中值滤波是针对灰度图像大滤波窗口半径(7×7以上)或者不规则滤波窗口使用的,该算法的性能比较稳定,同时比较高效。 图8的结果表明,当滤波窗口为3×3时,在该算法处理4通道图像时,HMPP的中值滤波算法性能最高达到了OpenCV中值滤波算法的146%,最低为106%,对于1024×1024这种大规模图像,性能提升达到了116%。 Figure 8 4-channel performance diagram of different filtering window sizes 实验结果表明,HMPP多通道中值滤波算法性能稳定,对于5×5滤波窗口,HMPP库使用的中值滤波算法的最高性能相比于OpenCV提升了140%,最低为101%,相比于OpenCV有较大的性能提升。对于1024×1024这种大规模图像性能提升达到了101%。实验结果表明,在5×5滤波窗口下,使用该算法及ARM NEON指令集优化后,对于小滤波窗口的中值滤波多通道,相对于OpenCV具有明显的性能优势,整体性能大约为OpenCV的120%。 对于7×7滤波窗口的4通道,从图8可以看到,本文提出的算法性能最高达到了OpenCV性能的132%,最低达到130%;针对1024×1024这种大规模图像,性能达到了130%。实验结果表明,在多通道情况下,该算法的整体性能依旧稳定。 对于11×11滤波窗口下的4通道,从图8可以看出,本文提出的算法性能最高达到了OpenCV性能的151%,最低达到了125%,针对1024×1024这种大规模图像,性能达到了125%。实验结果表明,在大滤波窗口多通道使用该算法的性能优异,相比于单通道的性能提升,多通道所带来的性能提升幅度更大,达到了预期要求。 本节以16u数据类型为例,分别测试不同算法在相同规模下的性能。OpenCV并没有实现8u数据类型以上的大滤波窗口下的中值滤波算法,而本文提出的算法可以有效地解决这个问题,并提升了性能。该算法通过设置哨兵,使得队中最小、队尾最大,缩小每次需要比较的规模的大小,递归调用这个过程,求出整个滤波窗口内的中值,解决了8u以上数据类型在大滤波窗口的中值滤波问题,如图9所示,滤波窗口大小为3×3时,本文提出的算法最高性能为OpenCV的201%,最低为150%;同样在滤波窗口为5×5时,本文提出的算法最高性能为OpenCV的140%,最低为120%,实验结果表明,本文采取的自适应算法整体性能优于OpenCV的中值滤波算法性能。 Figure 9 Performance of the proposed algorithm when the data type is 16u and the filtering window is 3×3 or 5×5 如图10所示,针对大规模的图像,本文算法的时间开销是稳定的,也就是说,随着规模的扩大,本文算法的优势会明显地体现出来,对性能有较大的提升。 Figure 10 Performance of the proposed algorithm when the data type is 16u and the filtering window is 11×11 对于本文采取的自适应算法对中值滤波性能的提升,以8u和16u数据类型为例,在不同滤波窗口大小及不同的通道数下,进行验证分析。本文使用8u和16类型下的3×3,5×5,7×7,11×11的性能数据。 图11为相同大小滤波窗口下的性能差异,当滤波窗口为3×3,5×5时,本文的自适应算法性能最佳。在7×7以上的滤波窗口下,相比于归并排序,本文使用直方图后性能最佳,从图11中可以看出,在不同大小的滤波窗口下,本文使用的自适应算法都能获得较佳的性能。如图12所示,在16u的不同大小的滤波窗口下,在小窗口下的算法相比于快速中值算法有明显优势,在大规模窗口下,本文采取的算法相比于归并排序有明显优势。实验结果表明,本文的自适应算法是有效的。 Figure 11 Performance comparison of different algorithms with the same filtering window when the data type is 8u Figure 12 Performance comparison of different algorithms with the same filtering window when the data type is 16u 本文针对中值滤波提出了一种自适应的算法,同时使用ARM NEON指令集优化,针对不同类型的图像和滤波窗口规模,对于8u的灰度图像,本文提出了基于改进后的直方图中值滤波算法,该算法相比于OpenCV中值滤波算法,性能提升了大约20%。 在滤波窗口为3×3和5×5时,使用提出的行列有序算法进行单独处理,该算法适用于所有数据类型。 对于非8u图像,当滤波窗口不规则或者min(H,W)>5时,本文提出了一种递归的算法,降低了求中值算法的时间复杂度,能稳定提升性能。 由于针对非8u大规模滤波窗口的现有算法并没有达到很好的性能,因此后续将重点研究非8u大规模滤波窗口的高性能算法,以提升其性能。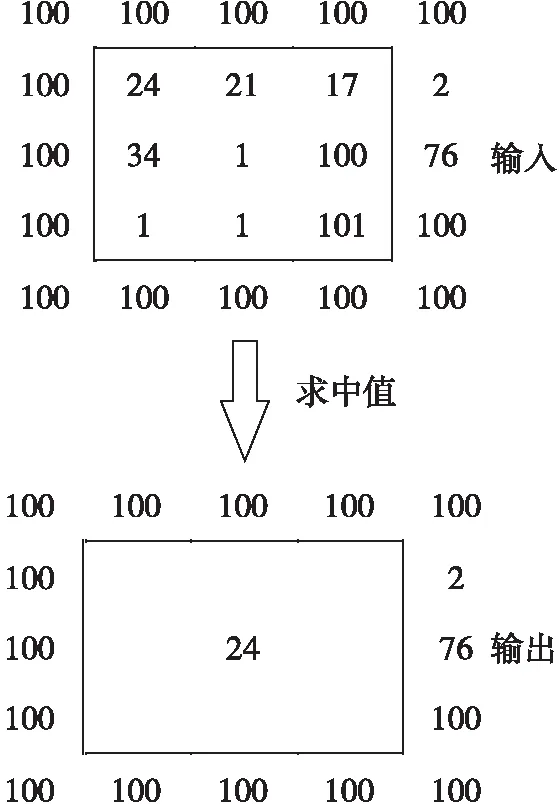
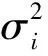
3.1 面向小滤波窗口的中值滤波通用算法

3.2 面向8u的中值滤波算法
3.3 面向非8u的大滤波窗口的中值滤波算法
4 中值滤波的优化策略
4.1 面向小滤波窗口的中值算法优化

4.2 基于8u直方图改进的中值滤波优化
5 实验结果与分析
5.1 8u类型下不同窗口的中值滤波结果与性能分析
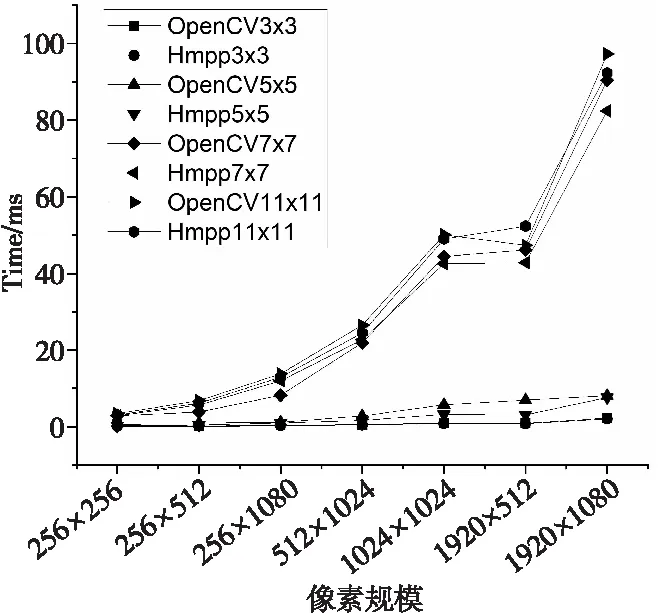
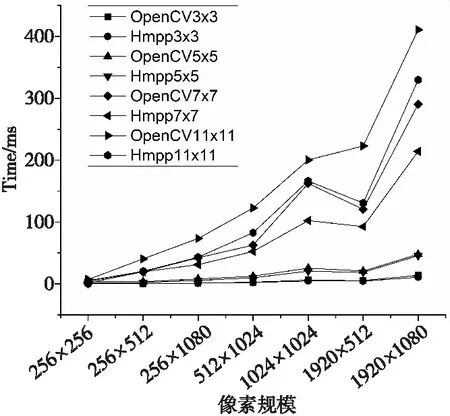
5.2 面向非8u中值滤波算法性能分析
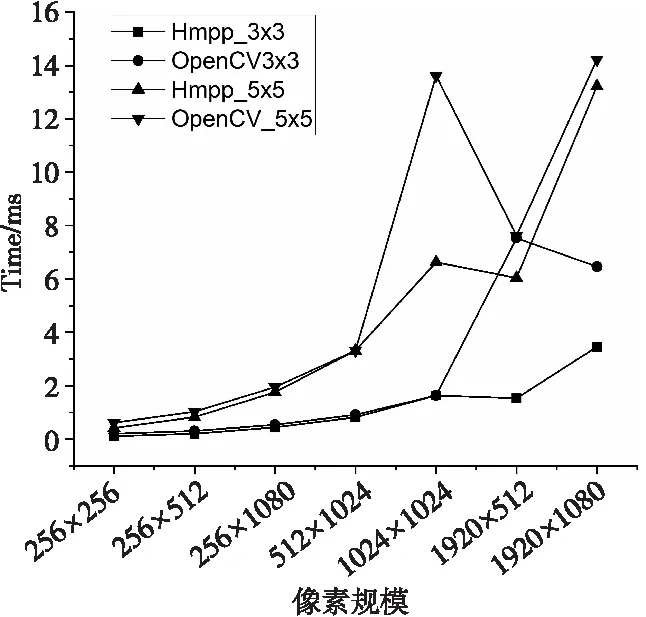
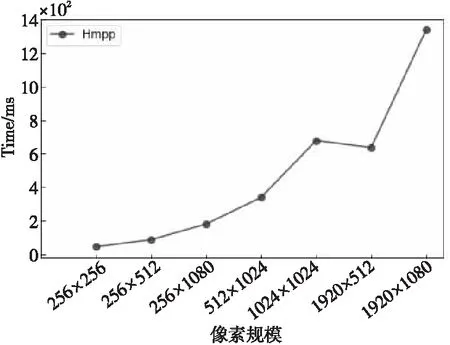
5.3 不同中值滤波算法在不同滤波窗口大小时的性能

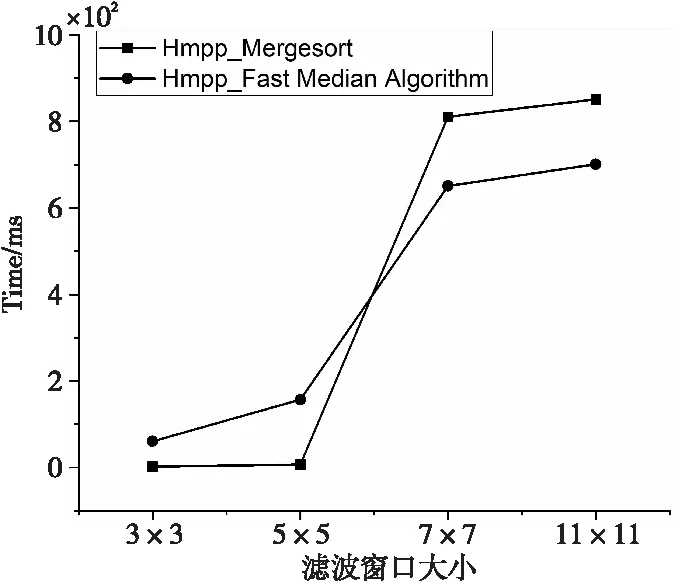
6 结束语
