基于观测器的线性系统非脆弱鲁棒控制及仿真
2021-11-17张学胜吉明明
张学胜,章 伟,吉明明
(1.上海工程技术大学机械与汽车工程学院,上海 201620;2.上海工程技术大学机器人智能控制实验室,上海 201620)
1 引言
状态反馈控制是以系统状态变量作为反馈量的反馈控制。由于实际应用中系统状态变量不易直接测量,因此常常使用观测器重构系统状态实现状态反馈控制。在观测期的研究上,近年来取得了许多成果。Zhang等人在文献[1]中研究了基于观测器的同步和未知输入还原,在文献[2]中研究了单边Lipschitz非线性系统中的指数观测器设计,在文献[3]中研究了单边Lipschitz非线性系统中未知输入观测器的设计。此外,Zhao[4]等人研究了满足递增二次有界条件的非线性系统中的混沌同步和保密通信,Acikmese[5]等人研究了满足递增二次有界条件的非线性观测器设计,Zemouche[6]等人研究了Lipschitz非线性系统中设计观测器的线性矩阵不等式((Linear Matrix Inequalities,LMIs))方法,都海波[7]等人研究了二阶非线性系统有限时间输出反馈控制及其应用,蒋继成[8]等人研究了基于观测器的加速度获取方法,董泽[9]等人研究了基于状态观测器的历史数据建模。为了将这些观测器的理论研究成果用于控制中,需要研究基于观测器的控制。
基于观测器的控制将观测器用在了反馈控制中,使观测器在许多领域得到了应用。例如,Zhao等人在文献[10]中将基于观测器的反馈控制用于故障检测中,Ekramian等人在文献[11]中研究了Lipschitz非线性系统中基于观测器的控制,Arcak等人在文献[12]中研究了斜度有界非线性系统中基于观测器的控制,Khalil等人在文献[13]中研究了高增益观测器的输出反馈控制,Sun等人在文献[14]中研究了基于观测器的鲁棒控制及其在航天器中的应用。此外,基于观测器的控制还可以被用于移动执行器、MIS机器人、加热炉的控制[15-17]。然而,在实际应用中基于观测器的控制仍存在许多问题。
在实际应用中,由于存在环境噪声、数据误差、系统更迭等不确定因素,系统的参数和控制率可能存在扰动,因此需要在基于观测器的控制中加入鲁棒控制和非脆弱控制[18]。在非脆弱控制的研究上,近年来出现了许多成果。刘艳[19]等人研究了网络化控制系统的非脆弱耗散控制,程昊宇[20]等人研究了变体飞行器的非脆弱鲁棒控制,肖会芹[21]等人研究了网络控制系统的非脆弱跟踪控制,王宇飞[22]将非脆弱控制用在了近空间飞行器多模型软切换中,Kchaou[23]、Mathiyalagan[24]等人研究了基于观测器的非脆弱控制,Lien[25]等人研究了线性系统中基于观测器的非脆弱控制,Zhou[26]等人研究了基于观测器的非脆弱控制在随机时滞系统中的应用,Arthi[27]等人研究了离散时间非线性系统中基于观测器的非脆弱控制,Zhu[28]等人研究了基于观测器的非脆弱反馈控制在不确定系统中的应用,Liu[29]等人研究了基于非脆弱观测器的滑膜控制。虽然对于非脆弱控制的研究有了许多卓越成果,但是基于观测器的非脆弱鲁棒控制的研究成果依然很少。
本文研究了不确定线性系统中基于观测器的控制,主要创新在于将非脆弱控制加入到基于观测器的鲁棒控制中。首先,针对所研究的不确定系统设计了非脆弱观测器并构造了Lyapunov函数。然后,对Lyapunov函数进行求导,使用线性矩阵不等式工具,将观测器存在问题转化为线性矩阵不等式求解问题。最后,得到了线性系统非脆弱鲁棒控制器存在的充分条件,并通过MATLAB仿真验证了结论的正确性和有效性。
2 问题描述及观测器设计
本文中将研究以下线性系统
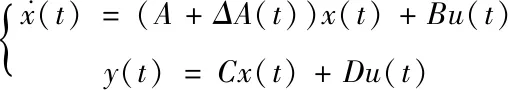
(1)
其中,x(t)、y(t)分别为系统的状态向量和输出向量,u(t)为系统的输入向量。A、B、C、D是维数已知的定常矩阵,ΔA为扰动矩阵。
针对该系统,观测器设计如下

(2)

假设扰动矩阵ΔA、ΔK和ΔL满足

(3)
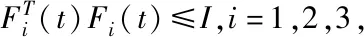

(4)

引理1[30]:对任意实矩阵D∈Rn×m,E∈Rm×n,时变矩阵F(t)∈Rm×m满足FT(t)F(t)≤I,和任意常数ε>0,有
DF(t)E+ETFT(t)DT≤ε-1DDT+εETE
(5)
引理2[31]:对具有适当维数的矩阵X、Y、Z、U和常数ξ,不等式
X+ZTYT+YZ<0
(6)
成立,如果下列不等式得到满足:

(7)

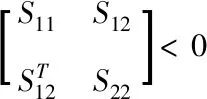
(8)
等价于

(9)
或者

(10)
3 主要定理及证明
定理1:系统(1)可通过观测器(2)和(3)实现渐近稳定,如果存在常数ε1、ε2、ε3、ρ、ξ,矩阵P、R、、使下列线性矩阵不等式成立
其中
系统的控制器和观测器增益可通过K=U-1和L=R-1求出。
定理1与已有的结论相比,增加了控制的非脆弱控制,可以实现不确定系统中基于观测器的非脆弱鲁棒控制。
证明:根据系统(1)与观测器(2),构造如下Lyapunov函数
V(z(t))=xT(t)Px(t)+eT(t)Re(t)
对其求导,得
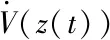
=xT(t)[ATP-KTBTP+PA-PBK]x(t)
+eT(t)[ATR-CTLTR+RA-RLC]e(t)
+eT(t)KTBTPx(t)+xT(t)PBKe(t)
+xT(t)Δ1x(t)+eT(t)Δ2e(t)+Δ3
其中
Δ1=ΔAT(t)P+PΔA(t)-ΔKT(t)BTP-PBΔK(t),
Δ2=ΔAT(t)R+RΔA(t)-CTΔLT(t)R-RΔL(t)C,
Δ3=eT(t)ΔKT(t)BTPx(t)+xT(t)PBΔK(t)e(t)。
由式(3)可得
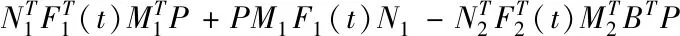
-PBM2F2(t)N2,

-RM3F3(t)N3C,

由引理1,得
故

其中

ψ2=PBK,ψ3=KTBTP,

令Ψ=Ψ1+Ψ2,其中
令K=U-1,对Ψ进行化简,得
其中
由引理2,得Ψ<0等价于
即
由引理3,使用Shur补对上式进行变换即可推导出定理1,定理1得证。
4 计算机仿真
针对系统(1)与观测器(2),将使用如下数据求解LMI得到控制增益与观测器增益
将数据代入系统(1)与观测器(2)中,求解LMI得到结果如下:


由下列数据,进行仿真:
得到仿真图形如图1和图2所示,由图1和图2可看出,随着时间的增加,系统状态的估计值趋近于真实值,误差估计趋近于零,说明本文的定理1的有效性。

图1 系统状态真实值与估计值

图2 误差估计示意图
5 结论
本文研究了一类基于观测器的非脆弱控制,采用了基于观测器的控制方法,利用线性矩阵不等式推导方法,得到了线性系统非脆弱控制器存在的充分条件。该充分条件通过LMI的形式给出,并且经过MATLAB仿真测试表明了该条件的有效性。
