基于粒子滤波的欠驱动移动机器人多目标点跟踪控制

君萌萌，张 敏，姜志伟，任鹏舟，左 磊

(长安大学 电子与控制工程学院，西安 710064)

0 引言

近年来，移动机器人目标点跟踪控制是机器人控制领域内的热点问题[1-3]，也是多目标跟踪、轨迹跟踪以及移动目标跟踪等诸多领域的研究基础[4-6]。目标点跟踪控制的实质是根据移动机器人的运动学特性，设计相应的控制方法，使得机器人能够从任意位置逐渐收敛到目标点附近。鉴于上述目标点跟踪控制的重要性，大量学者针对该问题展开了深入的研究。例如，文献[7]提出一种饱和反馈控制器来解决移动机器人的跟踪问题。文献[8]采用模型预测控制技术开发控制器，研究具有耦合输入约束的目标点跟踪控制。文献[9]提出具有一组不等式约束的控制方案来满足速度和扭矩约束。此外，文献[10]研究基于事件触发机制的跟踪控制方法。文献[11]研究避免碰撞的跟踪控制方法。文献[12]研究了保持安全距离的目标跟踪系统。文献[13]设计了模糊控制器实现轨迹跟踪控制。针对跟踪精度问题，文献[14]提出基于模型预测控制的轨迹跟踪系统，其中线性模型预测控制器可有效提高优化算法的运算效率。尽管现存文献已对移动机器人目标点跟踪控制进行了深入研究，但在实际应用中仍存在许多问题。例如，传统的目标跟踪控制方法跟踪精度较低，难以满足较高精度的跟踪控制需求或会导致跟踪控制系统出现奇异现象。因此，有必要深入研究移动机器人高精度跟踪控制。

由于目标跟踪精度控制问题中位置信息尤为重要，然而在实际中位置信息受传感器采样噪声影响较大，粒子滤波方法作为一种成熟的滤波算法，是使用一系列带权值的空间随机采样粒子来逼近机器人的真实位置[15]。由此可知，粒子滤波独立于系统模型，不受各种误差或噪声的约束，可适用于任何环境下的状态测量与估计。例如，利用粒子滤波方法实现有效跟踪预测[16-18]和目标定位[19-20]。尽管粒子滤波在定位精度方面取得了一定的研究成果，但在移动机器人领域内的应用范围有限，仍需开展进一步研究。

根据上述现状分析，本文利用粒子滤波算法，提出了一种面向欠驱动移动机器人的高精度目标点跟踪控制方法。其主要贡献为：在考虑移动机器人采样位置噪声的情况下，利用粒子滤波方法得到精准可靠的移动机器人位置信息。在此基础上，设计基于反馈控制的多目标点跟踪控制方法，并改进了其中控制参数的约束条件，使得欠驱动移动机器人能够快速、精准地到达目标点。最后，通过理论分析与数值仿真相结合的方式，验证了所提算法的稳定性与可行性。

1 车辆模型

考虑如下差分型欠驱动移动机器人，其运动学模型如下所示:

vko=(vl+vr)/2

ωko=(vl-vr)/D

(1)

其中:vl和vr分别代表左、右车轮的速度，D是两车轮之间的距离，vko和ωko分别表示前向速度和角速度；θk表示航向角；P=[px,py]T表示移动机器人的位置协调中心。

假设目标点序列为Wk∈R2,k={1,…n}，其中n为目标点的个数。移动机器人与目标点之间的位置关系如图1所示。从图1可知，移动机器人与目标点之间的位置关系可数学描述为：

(2)

其中:dWko是移动机器人到第k个目标点的距离，αko是移动机器人的转向角，σko是移动机器人车身固定框架到全局框架的方向。Wk=[Wkx,Wky]是第k个目标点的位置。

图1 移动机器人与目标点之间的位置关系

根据移动机器人的运动学特性及其与目标点的位置关系，基于移动机器人位置的极坐标运动学模型为：

(3)

需要注意的是，式(3)中的分母表示移动机器人到目标点的距离。当移动机器人到达目标点时，跟踪系统达到奇异点。为解决此问题，传统的研究方案使用一个半径为R的圆代替目标点。这种跟踪方式的精度往往取决于圆半径R。当需要达到高精度的跟踪性能时，传统的跟踪方法可能无法满足精度要求或会出现奇异现象。因此，本文将根据欠驱动移动机器人的运动学模型，提出一种新的跟踪控制方案来提高移动机器人到目标点的跟踪精度。

2 基于粒子滤波的车辆位置信息处理

本文考虑移动机器人的采样噪声，使用粒子滤波方法获得移动机器人的量测位置状态。假设k时刻移动机器人离散系统的状态方程和量测方程[21]为：

x(k)=f[x(k-1),l(k-1)]

z(k)=g[x(k),s(k)]

(4)

其中:x=[px,py]T为系统状态，z为观测数据(传感器获得的位置数据)，f(·),g(·)分别是状态转移函数和观测函数，l,s分别是系统状态噪声和量测噪声。设z1:k={z1,z2,…zk}为1～k时刻所有观测集合。

本文系统选取的状态转移函数规定在前后两帧观测时间内前向速度v和角速度ω保持不变。选取x=[px,py]T为状态变量，则式(4)中移动机器人系统的状态转移函数f[x(k-1)]为：

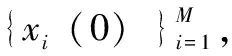
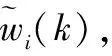
(5)

对权重进行归一化处理，可得：

(6)

5)状态输出。由于x(k)的最小方差估计就是x(k)的条件期望，则k时刻移动机器人系统的状态输出为：

(7)

在该算法中，k=0时刻初始化采样粒子，生成权值相等的均匀分布粒子集合。移动机器人运动过程中，每个粒子按照给定的状态转移函数进行状态更新，之后根据传感器测量值计算全部粒子的权重，最后加权权重就是系统的状态输出。与此同时，当有效粒子数小于阈值Ns时，对粒子集合进行重采样，淘汰权值过低的粒子，复制权值高的粒子组成新的粒子集,继续进行系统状态转移传播，构成一个循环滤波系统。

3 基于反馈控制的多目标点跟踪控制

根据上述基于粒子滤波的移动机器人量测位置信息，移动机器人与目标之间的位置关系式(2)可表示为：

(8)

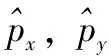
在此基础上，移动机器人跟踪目标的运动学模型可表述为：

(9)

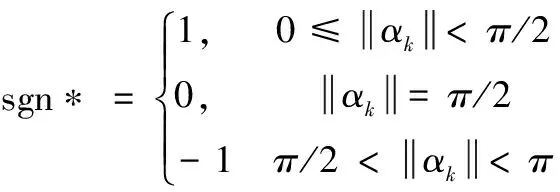
在此基础上，设计如下欠驱动移动机器人目标点跟踪控制律：

vk=kddWk

ωk=kααk+sgn*kσσk

(10)

其中控制增益kd,kα,kσ满足以下约束条件:

kd>0

sgn*kσ<0

sgn*kσ+kα-kd>0

(11)

具体地，给出如下移动机器人目标点跟踪控制定理:

定理1：考虑移动机器人目标点跟踪问题，其中移动机器人的运动学模型由式(1)表述。在考虑测量噪声的情况下，移动机器人的位置信息可通过式(7)获得，且移动机器人和目标点之间的运动学模型由式(9)表示。在此基础上，利用式(10)中提出的控制律以及式(11)中的控制增益约束条件，移动机器人将从任意初始位置渐近收敛到目标点。

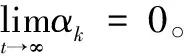
根据式(9)和(10)，可得移动机器人目标跟踪系统如下：

(12)

然后，考虑下面的 Lyapunov 函数:

υ1=(kσσk-kσαk)2+2sgn*kσkd(cosαk-1)

因为cosαk-1≤0,∀αk∈[0,2π]，调用式(11)参数条件:kd>0和sgn*kσ<0,得到:

sgn*kσkd(cosαk-1)≥0

因为(kσσk-kσαk)2≥0，υ1满足υ1≥0。

当σk=0,αk=0时，υ1=0，那么σk=0,αk=0是系统式(12)的平衡状态，υ1满足李亚普诺夫稳定性定理的正定性。然后对υ1求导，得到:

(13)

将式(12)代入式(13)，可得:

对αk∈[-π,π]，有sinαkαk≥0和sgn*kσkd<0。此外sinαk/αk可表示为:

根据式(11)参数条件sgn*kσ+kα-kd>0和kd>0，有:

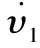
接下来证明式(12)在其平衡点αk=0的局部稳定性。在这个平衡点附近，将式(12)线性化如下：

(14)

用G表示式(14)的变换矩阵。G的特征方程为：

detG=(λ+kd)[(sgn*kσ+kα-kd)λ+

λ2-sgn*kσkd]

(15)

其中:λ是矩阵G的特征值。

假设线性系统式(14)稳定,则detG(λ)=0,G的所有特征值必包含实负部分。回顾式(11)中的参数约束，式(15)中的特征值为：

λ1=-kd<0

λ2+λ3=-(sgn*kσ+kα-kd)/2<0

λ2λ3=-sgn*kσkd>0

因此,有real(λ1)<0,real(λ2)<0,real(λ3)<0。这证明了所提跟踪系统的局部稳定性。证毕。

在上述证明中，详细分析了所提跟踪系统的全局稳定性和局部稳定性。通常，全局稳定性足以保证跟踪系统的可行性。然而,在全局稳定性部分只能找到参数条件sgn*kσ+kα-kd的作用。局部稳定性部分给出了条件kd>0和条件sgn*kσ<0的作用机理。因此，有必要对定理1中的全局稳定性和局部稳定性详细分析。

本文提供的控制增益不是从变换矩阵G的特征值推导出来的。事实上，通过变换矩阵的特征值即可得到控制增益。然而，这种方法只适用于线性系统。本文提出的跟踪系统式(12)是非线性系统。在非线性系统中，通过变换矩阵直接获得控制增益是比较困难的。因此，本文基于反馈控制得到了所提跟踪控制律中相关控制增益的范围。

此外，本文还提出一组辅助参数条件提高系统跟踪性能：

(16)

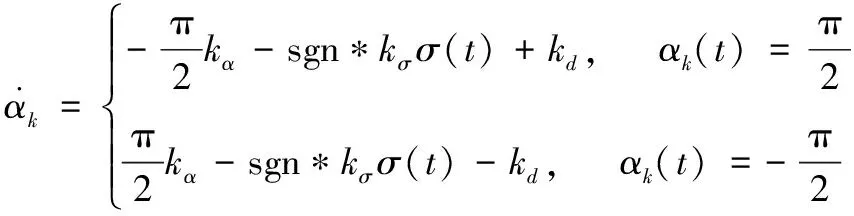
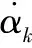
调用2sgn*kσk+kαk-(2/π)kdk>0,有：

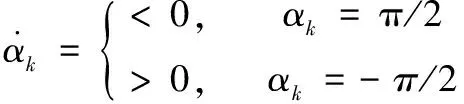
(17)

然后，移动机器人继续向目标点移动，这提高了跟踪效率。

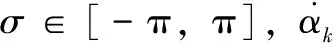
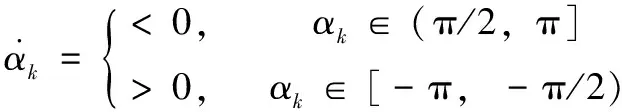
(18)

然后，移动机器人将转向它的目标点，并继续向它前进。

辅助条件2sgn*kσ+kα-kd可能包含在参数条件sgn*kσ+kα-kd。然而,如果只应用该控制律sgn*kσ+kα-kd,在跟踪过程中航向角αk可能会不在[-π/2,π/2]范围。因此，为了提高跟踪性能分别提出这两个条件。

(19)

对于算法中的目标跃迁临界值ε，本文所提出的跟踪方法可以不受任何限制地进行设置。然而，使用圆形标记目标的跟踪算法，跃迁临界值必须大于其圆形标记的半径。否则，移动机器人将永远不会停止跟踪它的第一个目标点。

注1：与一般的圆形目标跟踪方法相比，本节提出的跟踪控制方法可以实现移动机器人对目标点的高精度跟踪。一般的圆形标记目标跟踪方法，移动机器人会停在目标圆的边界附近，该算法的跟踪精度受目标圆半径R的限制。相比之下，本节提出的控制律可以在保证系统稳定性的前提下，使移动机器人尽可能到达目标点，具有较高的精度。

注 2：虽然所提跟踪控制方法在实际应用中存在诸多问题，但仍具有一定的优越性。首先，采用粒子滤波方法降低测量噪声，提高了跟踪方法精度；其次，该控制方法给出了相关参数增益的选择范围；最后，由于本文所提出的跟踪控制律本质上是反馈控制，因此在实验中保证了跟踪系统的稳定性和跟踪性能。

4 仿真结果与分析

本节将给出根据所设计的控制系统做出的仿真结果，以证明本文所提供的理论方法的可行性和有效性。

步骤1：检验粒子滤波的位置信息处理效果。根据移动机器人的离散状态方程(4)，给定系统状态转移方程的状态噪声为l=wgn(2,1,10*log10(3.42))，观测方程的量测噪声为s=wgn(2,1,10*log10(2.28))，移动机器人的初始位置为(50,10)。粒子滤波算法的仿真结果如图2所示。

图2 真实值与滤波后值的误差

图2(a)和图2(b)分别展示了系统真实值和滤波后的值在x方向、y方向的误差。从该图中可以看出初始采样之后，经粒子滤波方法得到的位置与真实位置相差极小。图中误差周期性地从某个值变小甚至为零，这是因为在迭代过程中粒子退化达到重采样条件时，复制较高权值粒子，减小权重误差。该结果表明移动机器人采样信息受噪声干扰之后，经过粒子滤波算法得到了较为精准的移动机器人状态信息。

步骤2：在验证了粒子滤波的位置信息处理效果后，开始对基于粒子滤波的多目标点跟踪控制方法进行检验。

1)考虑含有18个目标点的序列，移动机器人的运动学模型由式(1)描述。

2)根据式(11)控制律参数条件给定控制收益，当‖αk‖≤π/2时，控制收益为kd=1,kα=20,kσ=-2.5，当π/2≤‖αk‖≤π时，选择控制收益为kd=-1,kα=20,kσ=-2.5。

3)设定式(19)中的目标跃迁的临界值ε=0.001。

移动机器人多目标点跟踪的仿真结果如图3～5所示。

图3 目标点轨迹

在图3中，三角形点表示给定的目标点，从该图可以明显地看出，所提出的控制方案驱动差动型机器人通过给定的目标点，最终停在最后的目标点。需要注意的是图3所示的跟踪轨迹并不严格遵循目标点的线。这是因为移动机器人驱动力不足，只有前向速度和航向角受到控制。例如，当移动机器人从初始位置驶向其第一个目标时，它被直接驱动驶向第一个目标，而无需考虑第二个目标。因此，不能保证移动机器人抵达第一个目标的最终状态。然后，通过所提的控制律，移动机器人的航向角将调向第二个目标，因此导致图3中的弯曲轨迹。

图4(a)和图4(b)分别展现了移动机器人的前进速度v和转向角速度ω的演变。从该图可以看出，在t=100 s时，v和ω都收敛到零。从图4(a)可知，移动机器人在t=100 s到达最终目标点，然后在此时停止。而图4(b)中曲线在t=100 s之后有小幅动是因为移动机器人到达最后目标点之后的方向校正。此外，前向速度v和角速度ω周期性地从某个值变为零，这是因为移动机器人会定期更改其跟踪目标，改变前向速度和航向角。

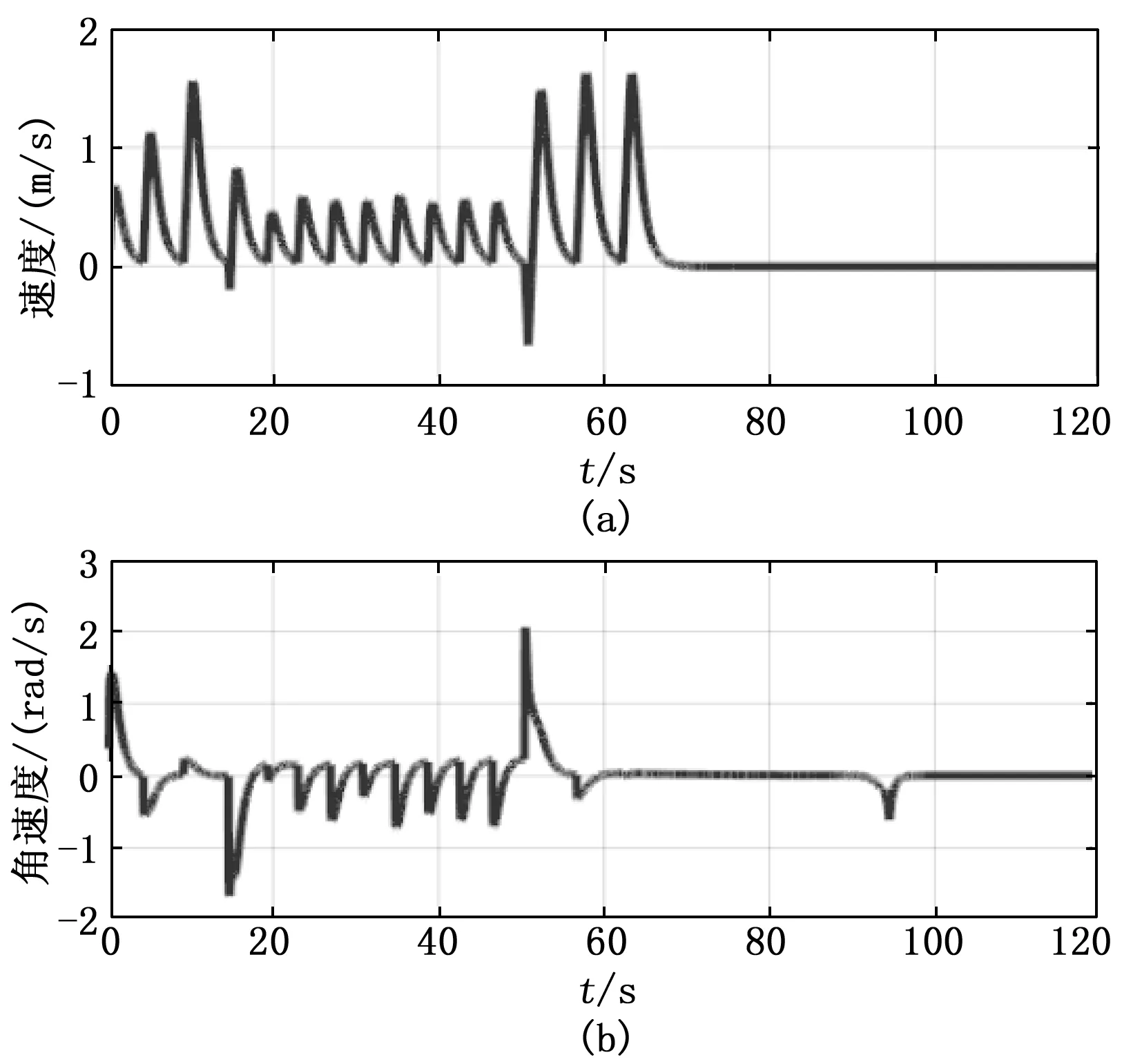
图4 移动机器人速度和角速度变化曲线

图5(a)和图5(b)分别展现了移动机器人到当前目标的跟踪误差(Ecc)、移动机器人到最后目标点的跟踪误差(Ecf)的演变。首先，在图5(b)中t=100 s时跟踪误差收敛到零可验证移动机器人停止在其最终目标位置。然后，在图5(a)中，跟踪误差周期性地变为零可表明移动机器人到达各个目标点。该结果表明：通过使用所提出的控制律，移动机器人将逐个通过一系列目标点，并在最后一个目标点停止。

图5 移动机器人和目标点的距离

4)关于目标点跟踪精度问题，以其中一个目标点为例，在目标跃迁临界值ε不同的情况下，移动机器人到目标点的跟踪精度如表1所示。

表1 不同临界值下跟踪精度

表1展现了在不同的目标跃迁临界值下，移动机器人到目标点的跟踪精度。由该仿真结果可知，移动机器人的跟踪精度总能达到或小于临界值，而该跃迁临界值可由读者自行设置，进而提高移动机器人的跟踪精度。

5 结束语

本文研究了基于反馈控制的欠驱动移动机器人高精度目标点跟踪控制问题。首先利用粒子滤波方法对移动机器人的位置信息进行降噪处理，从而得到较为精确的量测位置。在此基础上，结合反馈控制和欠驱动移动机器人的运动学模型，提出了具有一组参数约束条件的高精度目标点跟踪控制方案，使得移动机器人可从任意位置以较高的精度逐渐收敛到目标点，并严格分析了所提跟踪系统的稳定性和高精度的跟踪性能。最后，通过数值仿真的方式验证了本文所提算法的可行性和有效性。