访问策略隐匿的可追责层次属性加密方案*

唐广镇,陈 卓

(湖北工业大学计算机学院,湖北 武汉 430068)

1 引言

随着云技术的迅猛发展，广大企业和个人开始选择云服务商的服务实现计算和存储。但是，在将海量计算和存储转移到云端的同时，云服务商通常是不受信任的，因此有效解决云端数据安全问题成为云服务突破发展瓶颈的重要手段[1]。密文策略属性加密CP-ABE(Ciphertext-Policy Attribute-Based Encryption)[2]的创造性提出为实现用户的细粒度访问和云端数据的保密提供了新的思路，众多研究人员对CP-ABE方案的功能从不同方面进行了拓展。

在传统的CP-ABE方案中，没有对违规行为进行追责，用户会为了利益违规地将私钥共享给具有相同属性集的多个用户，因此追责泄露私钥的违规用户是提高CP-ABE方案安全性的一个重要步骤。另外，解密者接收到的密文包含访问策略，加密者的信息通常嵌在显性策略中，存在信息被违规用户泄露的可能性，因此隐匿访问策略也十分重要。

Waters等[3]首次用秘密同享方案表达访问策略。Zhang等[4]在合数阶群下提出了一种满足广域的半策略隐匿方案。许盛伟等[5]和闫玺玺等[6]都提出了多权威层次授权的方案，均可以隐匿策略。Wu等[7]提出了一种可追责的方案，能让第三方追溯私钥的来源。Yadav等[8]提出了一个具有高表达力的方案，能对滥用密钥的用户进行白箱追责，但计算开销较大。Ning等[9]在合数阶群下也提出了能进行白箱追责的方案，而且存储开销小。马潇潇等[10]提出了满足广域的可追踪方案。Khan等[11]在方案中运用隐匿向量加密技术,实现了完全隐匿。但是以上方案中，文献[4-6]方案不支持密钥的追责，文献[8-10]方案不支持访问策略的隐匿。为此，王梅等[12]提出了一种支持密钥追责和策略隐匿的方案，公钥和主密钥会略有增长。Li等[13]实现的隐匿策略方案能够进行黑箱追责且采用多权威机构授权。Changhee等[14]实现的隐匿策略方案能够进行白箱追责。石宇清等[15]提出了一种支持白箱追责的广域隐匿方案。文献[13,14]方案的实现均基于素数阶，提升了计算效率，但访问结构用多值与门表达，访问策略的安全性和表达力稍弱。胡媛媛等[16]提出的隐匿访问策略方案，融合了密文搜索和代理重加密技术，但不支持用户追责。

针对密钥泄露和访问策略显性暴露的问题，本文基于树访问结构，在合数阶双线性群下提出了一种可隐匿策略且可追责私钥的层次属性加密方案THH-CP-ABE(Traceable Hierarchical Hidden Ciphertext-Policy Attribute-Based Encryption)，并证明了本文方案在完全安全模型下是选择明文安全。本文方案的特点如下所示：

(1)策略隐匿。访问策略中插入合数阶子群中的随机元素，以合数阶子群的正交特性，隐匿访问策略。

(2)可追责。将用户标识加入其私钥运算中，可对违规用户追责。

(3)层次授权。使用层次授权体系，避免根权威的负荷过重和风险过高，提高了安全性和效率。

(4)高表达力。用树访问结构表达访问结构，提高了表达的灵活性。

2 背景知识

2.1 合数阶双线性群

设G和GT是阶数为N的乘法循环群，其中，N=p*r，阶N为2个不同素数p和r的乘积,g为G的生成元，映射e:G×G→GT满足下列性质：

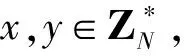
(2)非退化性：e(g,g)≠1。

(3)正交性：假设存在2个不同子群G1和G2的2个元素g1和g2，即g1∈G1，g2∈G2，则有e(g1,g2)=1，子群元素彼此正交。

2.2 安全模型

THH-CP-ABE方案的安全性证明是通过敌手A*同挑战者C*之间的互动游戏模型给出的，详细描述如下：

(1)初始化建立阶段：敌手A*挑选并发送给挑战者C*一个挑战访问结构。C*运行参数初始化算法，得到主密钥MK和公钥PK。C*保留主密钥MK并将PK发送给A*。

(2)第1阶段：敌手A*向挑战者C*发出属性集L={v1,v2,…,vn}的私钥输出问询。C*通过运行私钥生成算法生成私钥SK并发送给A*。

(3)挑战阶段：敌手A*递交长度一致的2个明文M1和M2给挑战者C*。C*随机选择Mγ，γ∈{1,2}，运行明文加密算法，得到密文Cγ，并发送给A*。

(4)第2阶段：敌手A*多次进行第1阶段的操作，继续私钥输出问询。

(5)猜测阶段：敌手A*猜测并给出γ′∈{1,2}。

如若在任意多项式时间内，敌手A*没有以不可忽视的攻击优势将选择明文攻击不可区分性IND-CPA(INDistinguishability under Chosen-Plaintext Attack)游戏赢下，则该方案被认为是选择明文(CPA)安全的。其中，攻击成功的优势为Adv=|Pr[γ′=γ]-1/2|。

3 本文方案

3.1 方案描述

本文提出的基于树访问结构的可隐藏策略且可追责私钥的层次属性加密方案(THH-CP-ABE)包括如下6个算法：

(1)Setup(1k)→(PK,MK)：输入方案安全参数k，进行初始化运算，输出公钥PK和主密钥MK。

(2)KeyGen(MK,L)→(SKTA)：输入主密钥MK、顶级权威的属性集L，输出顶级属性权威的私钥SKTA。

(3)Delegate(SKTA,L′,PK,MK,ID)→(SKU,Τ)：输入顶级属性权威的私钥SKTA、公钥PK、主密钥MK及次级新成员的属性集L′∈L，输出新成员的私钥SKU和查询表T。

(4)Encrypt(m,Λ,PK)→(CT)：输入需要加密的明文m、访问结构Λ及公钥PK，将访问结构Λ按转换规则转换为访问树分派秘密s，输出m的密文CT。

(5)Decrypt(CT,SKU,PK)→(mor ⊥)：输入公钥PK、包含用户属性集L′的用户私钥SKU和在访问结构Λ下加密生成的密文CT，属性集L′只有满足访问结构Λ要求时，方能计算并输出明文m，否则输出中止符号⊥，表示解密失败。

(6)Trace(PK,T,SKU)→(IDor ⊥*)：输入公钥PK、查询表T和私钥SKU。若SKU检验通过，输出用户ID；否则输出中止符号⊥*，表示不用追踪。

3.2 方案模型

图1为具有2级授权THH-CP-ABE方案的模型，由5个实体组成: 根权威、属性权威、数据拥有者、云服务提供商和用户(数据使用者)。根权威生成主密钥和公钥，为属性权威颁发私钥，拥有最高的权限，可以认为是完全信任的；各级属性权威为新加入的次级属性权威、数据使用者或者数据拥有者颁发私钥；数据拥有者依照选取的访问结构，将隐私文件加密成密文，并上传到云端。用户若想访问此文件，当且仅当其属性集满足访问结构要求，才能从云端下载文件后用解密算法对密文进行解密，从而实现隐匿策略的属性加密细粒度访问控制。云服务商提供密文上传、存储和下载的服务，同时可以追责泄露私钥的违规用户。方案采用层次授权体系，有效分散授权私钥的计算量，避免根权威的负担过重和风险过高，提升了安全性和效率。

THH-CP-ABE方案进行如下安全性假设：(1)假设云服务提供商会切实有效地履行用户的上传或下载请求，但同时存在好奇心，串通恶意用户对隐私文件进行窥视或窃取，是半可信的；(2)假设数据使用者只能用只读方式访问隐私文件；(3)假设每个实体之间所有通信信道风险极低，都是安全可靠的。

3.3 方案构造

(1)Setup(1k)。

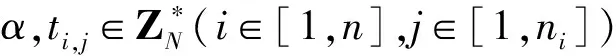
(2)KeyGen(MK,L)。

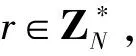
(3)Delegate(SKTA,L′,PK,MK,ID)。

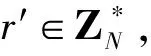
(4)Encrypt(m,Λ,PK)。

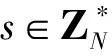
①若节点标识符是∧(与操作)，使用(t,n)Shamir秘密共享方案来共享秘密s，n是孩子节点的个数，门限值t=n。向所有孩子节点依次分派si=f(i)并标注为已分派。

②若节点标识符是∨(或操作)，t=0，向所有孩子节点依次分派s并标注为已分派。

③若节点标识符是of(门限操作)，且使用(t,n)Shamir秘密共享方案来共享秘密s，t是用来重构秘密s的孩子节点数。向所有孩子节点依次分派si=f(i)并标注为已分派。

密文由树中叶子节点的值组成，i表示叶子节点的位置索引，t表示孩子节点个数，aj表示从U中随机取出的属性。

(5)Decrypt(CT,SKU,PK)。

计算检验函数的值F，若F=(L′⊆Λ)=0，返回⊥。若F=(L′⊆Λ)=1，计算明文m′：

其中，li(0)是树索引i计算出来的拉格朗日系数。输出明文m′。

(6)Trace(PK,T,SKU)。

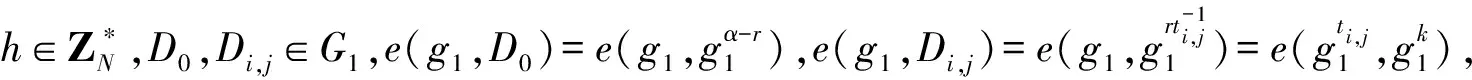
4 方案分析

4.1 正确性证明

执行解密算法Decrypt()阶段，数据使用者获得密文CT后，唯有数据使用者自身的属性集L′满足了访问结构Λ的要求，才能用解密算法对密文进行解密，本文方案的正确性证明如下所示：

由于合数阶双线性群的正交性原理，THH-CP-ABE方案在加密算法中引入合数阶子群中的随机元素R′0和R′j，将访问结构隐形嵌入在密文中实现策略隐匿。从上述的正确性证明中可以看出，解密结果的正确性不受随机元素影响，能有效地防止敌手通过访问结构中的信息推断出用户隐私。

4.2 安全性证明

假设敌手A*能用不可忽视的优势ε/2胜得IND-CPA游戏打破本文方案，则存在挑战者C*可用优势ε/2解决DBDH假设。具体证明过程如下：

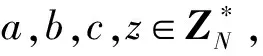
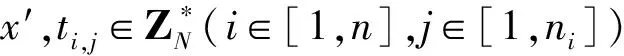
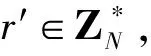
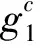
①若节点标识符是∧，f(i)的阶数设为n-1，n是叶子节点的总数。

②若节点标识符是∨，f(i)的阶数设为0，f(0)=c。

③若节点标识符是of，f(i)的阶数设为t-1，t是可恢复秘密的叶子节点的总数。

(5)第2阶段：多次进行第1阶段私钥输出问询。

(6)猜测阶段：敌手A*对γ′进行猜测,γ′∈{1,2}，有以下2种情况：

①若γ′=γ，说明敌手A*能猜想Z=e(g1,g1)abc，挑战者C*能获得有效密文，其优势为Pr[γ′=γ|Z=e(g1,g1)abc]=1/2+ε。

②若γ′≠γ，说明敌手A*能猜想Z=e(g1,g1)θ，只能获得随机密文，无法获得有效密文，挑战者C*的优势为Pr[γ′≠γ|Z=e(g1,g1)θ]=1/2。

因此，挑战者C*可以解决DBDH假设，其解决优势为ε/2。THH-CP-ABE方案在此安全模型中是安全的。

4.3 效率分析

本节将比对THH-CP-ABE方案与其他属性加密方案，以说明THH-CP-ABE方案的优势。

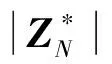
从表1中可以看出，本文方案与文献[6,12]方案相比较，主密钥和密文长度会更短，本文方案与文献[6]方案的公钥长度一样长，但比文献[12]方案的公钥长度稍短。本文方案的构造是基于合数阶群，私钥长度会稍长，但提高了安全性，同时引入层次化授权结构，提高了分发私钥的授权中心的效率。一般情况下，|u|和|E|小于n，且在复杂的方案中，下级用户个数和访问结构中属性数量越多，|u|、|E|和n的差会越大，因此本文方案的通信和存储代价更小，更便于传输和私钥保存。

从表2中可以看出，本文方案的加密和解密计算开销都比文献[6]方案的更优，同时本文方案还支持密钥追责。对比文献[12]方案，参与加密属性数量较少时，本文方案加密计算开销略高，在属性数量增多后，本文方案体现出加密优势，在解密开销方面也小于文献[12]方案的。文献[16]方案同样可以使访问策略隐匿，但在解密中，比本文方案增加了|L|+1次双线性对运算，加密中群G上的运算次数也有所增加。文献[5]方案也是基于访问树提出的，与本文方案一样，同样支持策略隐匿和层次加密。在解密开销方面，本文方案的双线性对运算次数减少了|L|+1次，在加密开销方面，本文方案则远远优于文献[5]方案。

Table 1 Keys and ciphertext length comparison of different schemes

Table 2 Characteristic and time cost comparison of different schemes

为了更精准地评估本文方案的运行效率，通过实验对本文方案和文献[6,12]的方案进行计算开销仿真测试比对。仿真测试的PC机配置3.30 GHz的Intel Core i5-4590 CPU与8 GB RAM，使用Java的JPBC密码库。图2和图3分别表示THH-CP-ABE方案与2种对比方案在不同数量属性参与的加密和解密过程的时间消耗对比。

从图2可以看出，随着属性数量的增加，文献[6,12]方案的加密开销随之线性上升，本文方案在参与加密的属性数量为5～20个时，加密开销略高于对比方案，随着属性数量|E|增加，本文方案将具有明显优势。

从图3中能看出，本文方案和对比方案的解密计算开销均随参与解密的属性数量的增加而线性变化，本文方案解密开销略低于文献[12]方案的解密开销，明显低于文献[6]方案的解密开销。

5 结束语

本文在合数阶双线性群下基于树访问结构，提出了一种可隐匿策略且可追责私钥的层次属性加密方案THH-CP-ABE。THH-CP-ABE方案使用层次授权体系，减少了根权威的负荷和风险；采用树访问结构，使访问策略具有高表达力和高拓展性；运用合数阶群的正交性原理，将合数阶子群的随机元素加进密钥生成算法中，实现了隐匿访问策略；通过用户标识能够及时有效地追责违规泄露私钥的用户。实验结果和效率分析显示，THH-CP-ABE方案在加解密效率上优于对比方案，且在功能上更丰富。后续研究方向是在现有方案中加入在线离线加密和属性撤销支持，使方案能更高效、更安全地运用。