支持多跳的多策略属性基全同态短密文加密方案

荀艳梅，陈燕俐，彭春春

(南京邮电大学计算机学院、软件学院、网络空间安全学院，江苏 南京 210023)

云计算作为一种远程服务模式，能够给用户提供存储空间和计算能力。为了保证用户隐私，防止数据的泄露，数据通常被加密后存储在云端。传统的密码技术虽然能够确保数据在云端的保密存放，但却无法实现密文之间的运算和处理。全同态加密（Fully Homomorphic Encryption，FHE）不仅可满足传统加密的功能，并可在不知道密钥的情况下，对密文进行任意计算。自2009年Gentry［1］基于理想格提出第一个真正意义上的全同态加密方案后，全同态加密研究引起了学者和专家的极大关注。在安全性假设和效率等方面，产生了很多FHE实现和优化方案，例如 BGV12［2］、GSW13［3］、BV14［4］等。

属 性 基 加 密 （ Attribute⁃Based Encryption，ABE）［5］作为一种公钥加密，既可以满足多用户需求，又可以设置用户的访问权限，有着广泛的应用场景。ABE可以分为密钥策略属性基加密（Key⁃Policy ABE，KP⁃ABE） 和密文策略属性基加密（Ciphertext⁃Policy ABE，CP⁃ABE），在 KP⁃ABE 方案中，密钥与访问策略相关，密文与属性集相关，当且仅当属性满足访问策略时才可解密密文。而CP⁃ABE正与之相反。2013年，Gentry等［3］结合 FHE和文献［6］中的KP⁃ABE方案，首次构造了属性基全 同 态 加 密 （ Attribute⁃Based Fully Homomorphic Encryption，ABFHE）方案，该方案可在实现属性基加密的同时，对同属性集密文进行计算。此后围绕计算效率、访问策略灵活性、困难性假设等，专家们提出了一系列的ABFHE方案。

然而传统的FHE方案只能对相同公钥加密的密文（所有密文属于同一个用户）进行同态运算，这在很大程度上限制了FHE方案的实际应用，在许多的现实多用户场景中，通常需要对多个用户上传到云端的用不同密钥加密的数据进行安全的多方联合计算。因此 López⁃Alt等［7］提出多密钥全同态加密（Multi⁃Key Fully Homomorphic Encryption，MKFHE）的概念，支持对不同用户（不同密钥）的密文进行任意的同态运算，且运算之后的结果必须由参与计算的所有用户联合解密，可以较好地解决多用户密文进行同态计算的问题。

2016年，将MKFHE和ABFHE相结合，Brakerski等［8］提出多策略（即多密钥）全同态属性加密方案（Multi⁃Target Homomorphic ABE，MT⁃HABE），实现了不同访问策略下对应的不同属性集下加密密文的同态运算。此同态计算结果需要联合所有拥有匹配这些不同属性集的访问策略密钥的用户才能解密。但Brakerski等的方案是单跳（Single⁃hop）型的，即需要提前对参与同态计算用户的数量进行设置，并且在运算过程中无法实现新用户的加入。2017年，Hiromasa等［9］提出了具有多跳性质的多策略目标属性基全同态加密方案，同态运算后输出的密文能够与新加入参与方的密文重新进行运算，即任何参与方都可以实时、动态地加入到密文运算的过程中，但该方案密文尺寸较大，密文同态计算效率较低。

针对上述问题，本文在Peikert等［10］提出的多跳MKFHE的基础上，结合KP⁃ABFHE，提出了一种基于LWE（Learning With Error）问题的支持多跳多策略属性基全同态短密文加密方案，主要贡献如下：

（1）方案首先是基于KP⁃ABE，根据属性集合x对消息进行加密，并根据访问策略f生成密钥。只有当f（x）＝0时，密文才能通过密钥解密，访问策略是基于布尔电路，可实现对数据的细粒度访问。其次方案可实现满足不同访问策略的不同属性集密文进行全同态计算的功能，并具有更短的密文和更高的同态计算效率，密文扩展更容易实现。

（2）方案具有多跳性质，即任何参与方都可以实时、动态地加入到密文运算的过程中，同态运算后输出的密文能够与新加入参与方的密文再次进行同态运算，即使新加入密文所对应属性集不满足已有的访问策略集。

（3）方案安全性基于LWE问题，证明了选择属性下的选择明文攻击不可区分性（INDistinguishability under Chosen Plaintext Attack，IND⁃CPA）安全性。

1 相关工作

1.1 属性基全同态加密

属性基加密方案可实现加密数据的细粒度的访问控制，但不支持对加密数据的计算。2013年，Gentry等［3］采用近似特征向量方法，实现了无需评估密钥的全同态加密方案GSW13，并在此基础上给出第一个属性基全同态加密方案的实现思路，方案采用近似特征向量方法，无需评估密钥，既可以设置访问权限，又可以对密文进行同态评估，但同态性受到一定限制，该方案只能对具有相同属性集的密文进行同态计算。2016年，Clear等［11］在标准模型中提出了一个ABFHE方案，该方案可以评估无限深度的电路，但是电路的输入数量受到限制。2017年，Tan等［12］为解决云服务提供商外包数据计算问题，提出了一种基于环上误差学习（Ring⁃LWE，R⁃LWE）的密文策略属性基同态加密（Ciphertext Policy⁃Attribute Based Homomorphic Encryption，CP⁃ABHER⁃LWE）方案，以支持多用户场景下具有细粒度访问控制的外包云数据计算。该方案将ABE方案融入同态加密方案中，以提供加密数据的计算和存储的细粒度访问控制。该方案大大减少了计算时间和密文大小，提高了企业和云服务提供商之间的实际效率，但是只能对相同策略的密文进行计算，不能满足多策略应用环境。2021年，Liu等［13］基于LWE问题提出了一种属性基全同态短密文加密方案，该方案通过对属性进行分类，并使用小工具矩阵，消除了密文对属性个数的依赖，密文不再随着属性数的增加而增加，减少了加解密时间。然而方案只支持相同策略下的密文计算，且访问策略为与门，不能满足更灵活的访问控制要求。

1.2 多密钥全同态加密

多密 钥 全 同 态 加 密 （Multi⁃Key Fully Homomorphic Encryption，MKFHE）支持对不同用户（密钥）的密文数据进行处理，处理后的结果可由所有参与计算的用户联合解密，其相对于传统的（单密钥）全同态加密，更加适用于云环境下多用户数据的隐私保护和处理，应用范围更广，如密文检索、安全多方计算、隐私保护协议［14］等。

MKFHE分为3种类型，第一种类型为López⁃Alt等［7］根据 Hoffstein 等［15］提出的 NTRU 方案首次提出的NTRU型MKFHE方案，以及随后出现了很多优化方案，例如 DHS16［16］、CO17［17］等。 第二种类型是 Chen 等［18］将 Brakerski等［2］于 2012 年提出的BGV12方案扩展到多密钥设置，提出了第一个BGV型多跳的MKFHE方案CZW17，以及随后出现了很多优化方案［19－20］。 第三种类型为 GSW 型 MKFHE方案。 2015 年，Clear等［21］将 GSW13［3］方案扩展到多密钥设置，首先将单个用户密文进行扩展，使其对应所有参与计算的用户，然后再进行同态计算，最终通过所有用户的联合密钥对密文进行解密，提出了基于LWE问题的MKFHE方案CM15，但是扩展过程较复杂。 2016年，Mukherjee等［22］优化了 CM15中的扩展算法，提出了新的基于 LWE问题的MKFHE方案MW16，该方案允许对多密钥密文进行一轮的分布式解密，可进一步构造两轮多方计算协议，且具有更低的计算复杂度和更小的密文尺寸。然而CM15和MW16方案是单跳（Single⁃hop）的，需要提前对参与同态计算用户的数量进行设置，并且在运算过程中无法实现新用户的加入。2016年，Peikert等［10］提出了多跳（Multi⁃hop）型 MKFHE 方案，同态运算后输出的密文能够与新加入参与方的密文重新进行运算，即任何参与方都可以实时、动态地加入到密文运算的过程中，但是参与方的数量受到一定限制。

1.3 属性基多策略（密钥）全同态加密

为了解决多用户具有细粒度访问控制的数据计算问题，2016年，Brakerski等［8］提出了两种类型的访问策略参与同态计算的目标属性基全同态加密方案（Targeted Homomorphic Attribute⁃Based Encryption，T⁃HABE）：单策略 T⁃HABE（Single Target Homomorphic ABE，ST⁃HABE） 和 多 策 略 T⁃HABE （Multi Target Homomorphic ABE，MT⁃HABE）。 ST⁃HABE 方案可对属性满足某个单一策略的密文进行同态计算，而在MT⁃HABE中，一组策略与同态计算相关，可以在属性满足策略集合中某个策略的密文之间进行处理。显然MT⁃HABE方案能满足更多的应用场景，可对不同用户（密钥）下加密的密文进行计算，每个用户根据访问策略生成自己的私钥，即属于多密钥全同态加密方案，但是该方案是单跳的，同态计算过的密文不能再次与新密文进行同态计算。2017年，Hiromasa等［9］将 Peikert等［10］提出的多跳 MKFHE 方案中第一个大密文小密钥方法与ST⁃HABE方案结合，提出了具有完全动态同态计算的MT⁃HABE，可在同态计算期间将任意附加密文作为输入，实现对不同访问策略对应的不同属性下的加密密文的同态计算。然而该方案具有较大的密文，密文计算时比较复杂，需要对密文中每一项进行计算，有较低的计算效率。

2 预备知识

2.1 符号

本文用ℕ表示自然数集，用ℤ表示整数集，用ℝ表示实数集。对于任何正整数d＞0，［d］表示｛1，2，…，d｝。 设S是一个集合，P是S上的概率分布。a←S表示a∈S从S中随机均匀采样，b←P表示b∈S从P中采样。符号negl（λ）表示λ∈ℕ 的可忽略函数集。向量由粗体小写字母书写，向量x的第i个元素由xi表示。‖x‖∞表示向量x的l∞范数（最大范数）。＜x，y＞表示两个向量的内积。矩阵表示为粗体大写字母，矩阵X的第i列向量由X［i］表示。对于矩阵的l∞范数定义为符号XT表示X的转置。 对于两个矩阵表示矩阵A和B串联生成的矩阵。In表示n×n维单位矩阵，0n×m表示所有项都为0的n×m维矩阵。 对于任何表示第i个维度为n的标准基向量。

2.2 张量积

m1×n1维矩阵A和m2×n2维矩阵B的张量积⊗是由m2×n2个区块组成的m1m2×n1n2维矩阵，其第 （i，j） 个区块为ai，jB，其中ai，j是矩阵A的第（i，j） 个元素。

对于任何标量r∈ℝ，有

根据张量积的混合积属性，有

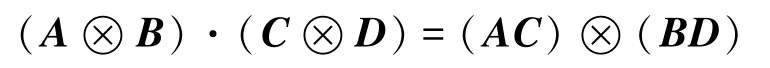
对于任何具有兼容维数的矩阵A，B，C，D，有

2.3 LWE 问题

误差学习（Learning With Errors，LWE）问题由Regev［23］提出，已经被证明为一个难解的多项式复杂程度的非确定性（ Non⁃Deterministic Polynomial，NP）问题。

定义1判定性 LWE（Decisional LWE，DLWE）问题。 设安全参数λ，参数n＝n（λ），q＝q（λ）≥2为整数模数，χ＝χ（λ）为ℤ上的高斯分布。D0＝其中其中χ。 DLWE问题就是上述两个分布：D0，D1不可区分。

2.4 Gadget矩阵和位分解

对于任意模数q，l＝「logq⏋，行向量矩阵

函数g－1：ℤq→ℤl，表示将一个数分解为二进制数，对于任意a∈ ℤq，列向量x＝g－1（a） 是｛0，1｝向量，并且有＜g，x＞＝a。 符号［a］g－T＝g－1［a］T，输出一个二进制的行向量，满足［a］g－T·gT＝［a］。 符号（In⊗g－1）［A］表示对矩阵A的每个元素进行二进制分解，得到行扩张的矩阵，有（In⊗g）·（In⊗g－1）［A］＝A。类似地，［A］（In⊗g－T） 表示对矩阵A的每个元素进行二进制分解，得到列扩张的矩阵，有［A］（In⊗g－T）·（In⊗gT）＝A。

2.5 格陷门和离散高斯分布

定理1生成陷门［24］。存在一个有效的算法TrapGen（1n，q，m），对 于 所 有 的m≥m0，m0＝O（nlogq），输出一个陷门矩阵对其中A在统计上接近于均匀分布，并且对于给定的τ≥τ0， 给定可以得到

定理 2高斯采样［24］。m，n，q，N为选取参数，满足随机选取矩阵A∈在统计上接近于均匀分布，对于所有的矩阵可得到分布其中且对于所有的的最后N个坐标的边缘分布统计接近于｛0，1｝N上的均匀分布。

2.6 同态操作

定义 2［25］令令B＝［B1，B2，…，Bl］。 假设访问策略f∈｛0，1｝l→ ｛0，1｝ 的电路深度为d，且只包含与非门电路。将B1，B2，…，Bl接入电路的线路端口，f中每个线路端口w，u，v为其的左右输入，定义则可以递归到矩阵B，算法表示为

推 论 1［8］令则存在一个多项式时间的算法EvRelation，令那么有（Bf－

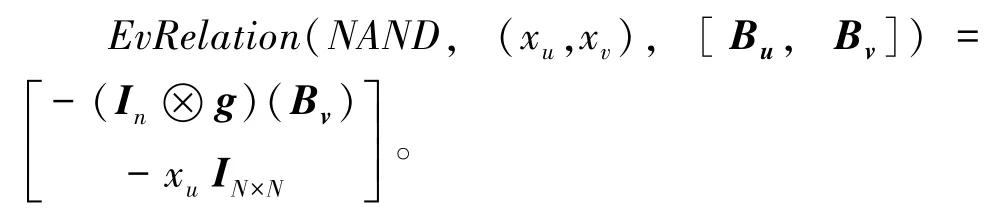
2.7 T⁃HABE 方案的形式化定义和安全模型［8］

2016年，Brakerski等［8］提出目标属性基全同态加密方案T⁃HABE，其同态计算依赖访问策略，本文提出的方案也是以此为基础的，因此下面给出T⁃HABE的形式化定义和安全模型。

定义3T⁃HABE。 T⁃HABE 方案由5个算法构成，分别是 Setup，Enc，KeyGen，Eval和 Dec，具体如下：

Setup（1λ） → （pp，psk）。 算法以安全参数λ（另外还包括访问策略电路深度等参数）作为输入，输出公共参数pp和主密钥msk。

Enc（pp，μ，x） → （ct，x）。 算法以公共参数pp、明文μ和属性集x作为输入，输出一组原始密文和属性集 （ct，x）。

KeyGen（msk，f） →skf。 算法以主密钥msk和访问策略f作为输入，并输出私钥skf。

Eval（pp，F，ct（1），…，ct（k），g） →ct（F）。 将公共参数pp、 访问策略集F、原始密文ct（1），…，ct（k）和同态运算函数g作为输入，输出g对应的同态密文ct（F）。

Dec（skF，ct（F）） →μ。 算法以密钥skF＝｛skf：f∈F｝ 和密文ct（F）作为输入，输出明文μ∈ ｛0，1｝。

定义4T⁃HABE 的正确性。令｛Fλ｝λ∈N为访问策略类，｛Gλ｝λ∈N为同态计算类，如果满足以下条件，那么方案 T⁃HABE＝ ｛Setup，Enc，KeyGen，Eval，Dec｝是正确的。

令Setup（1λ） → （pp，psk），考虑一系列策略集F⊆Fλ，对应的私钥集为个明文和属性且任意x（i），都存在f∈F，有f（x（i））＝0，密文对于一些g∈G，计 算满 足

定义5如果对于多项式时间的攻击者在如下游戏中的优势是可忽略的，那么这个方案在选择安全模型中是选择明文攻击下的不可区分（IND⁃CPA）安全的：

目标。攻击者声明一个目标属性x∗，且发送给挑战者。

初始设置。 挑战者利用Setup（1λ，1dF，1dG） 生成pp，msk，并且将pp发送给攻击者。

查询1。攻击者通过向挑战者发送fi函数来进行多项式密钥查询。一旦挑战者收到这些函数后，挑战者会利用KeyGen（msk，fi） 生成一个密钥skfi，且当fi（x∗）＝1时，其将发送skfi返回给攻击者，否则发送⊥。

挑战。攻击者发送一对等长的消息μ0，μ1给挑战者。 挑战者随机选择b∈ ｛0，1｝， 并利用Enc（pp，μb，x∗） 算法将消息μb生成挑战密文ct∗，最后挑战者将ct∗发送给攻击者。

查询2。攻击者进行多项式密钥查询，与查询1阶段相同。

猜测。攻击者输出关于b的猜测b′∈｛0，1｝。

如果b＝b′，就可以称攻击者赢得了游戏。在游戏中，攻击者的优势定义为Adv（λ）＝如果对于任何多项式时间里的攻击者，有Adv（λ）＝negl（λ）， 则认为方案 T⁃HABE是选择性安全的。

与之前的基于LWE的属性基加密相同，方案满足f（x）＝0时才可解密，且所有查询都必须满足fi（x∗）＝1。

3 多跳多策略属性基全同态加密dMTHABE方案

本方案是在Brakerski等［8］提出的单跳多策略目标属性基全同态加密方案T⁃HABE上构建的多跳多策略属性基全同态加密方案（简称dMTHABE方案），在所提出的方案中，同态密文可与新加入密文再次进行同态操作，实现了多跳功能。

应用场景模型如图1所示。利用ABE的性质，设策略集F＝｛fi｝i，属性授权中心（AA）为每个访问者（User）根据该用户的访问策略fi分配密钥skfi。数据提供者（Owner）可以用属性集xj加密共享数据μj，将密文 （ctj，xj） 上传至服务器（Server）。 只有访问者的访问策略与密文的属性集合满足一定关系，即fi（xj）＝0时，访问者才可以解密该密文，查看共享数据。利用MKFHE的性质，服务器可以对不同属性集合下加密的密文进行同态操作，得到新的同态密文ct（F）。 此同态计算结果需要联合所有拥有匹配这些不同属性集合的访问策略密钥｛skfi｝i的用户才能解密，得到同态计算明文g（｛μj｝j）。 当有新的数据共享者加入时，新加密的密文可以直接与以前的同态计算密文再进行同态操作，并能正确解密。

3.1 dMTHABE方案具体构造

Setup系统初始化算法由属性授权中心（AA）运行，生成公共参数pp和主密钥msk。 首先根据4.1节选取 DLWE 参数n，q，χ，有为B有界的错误分布。

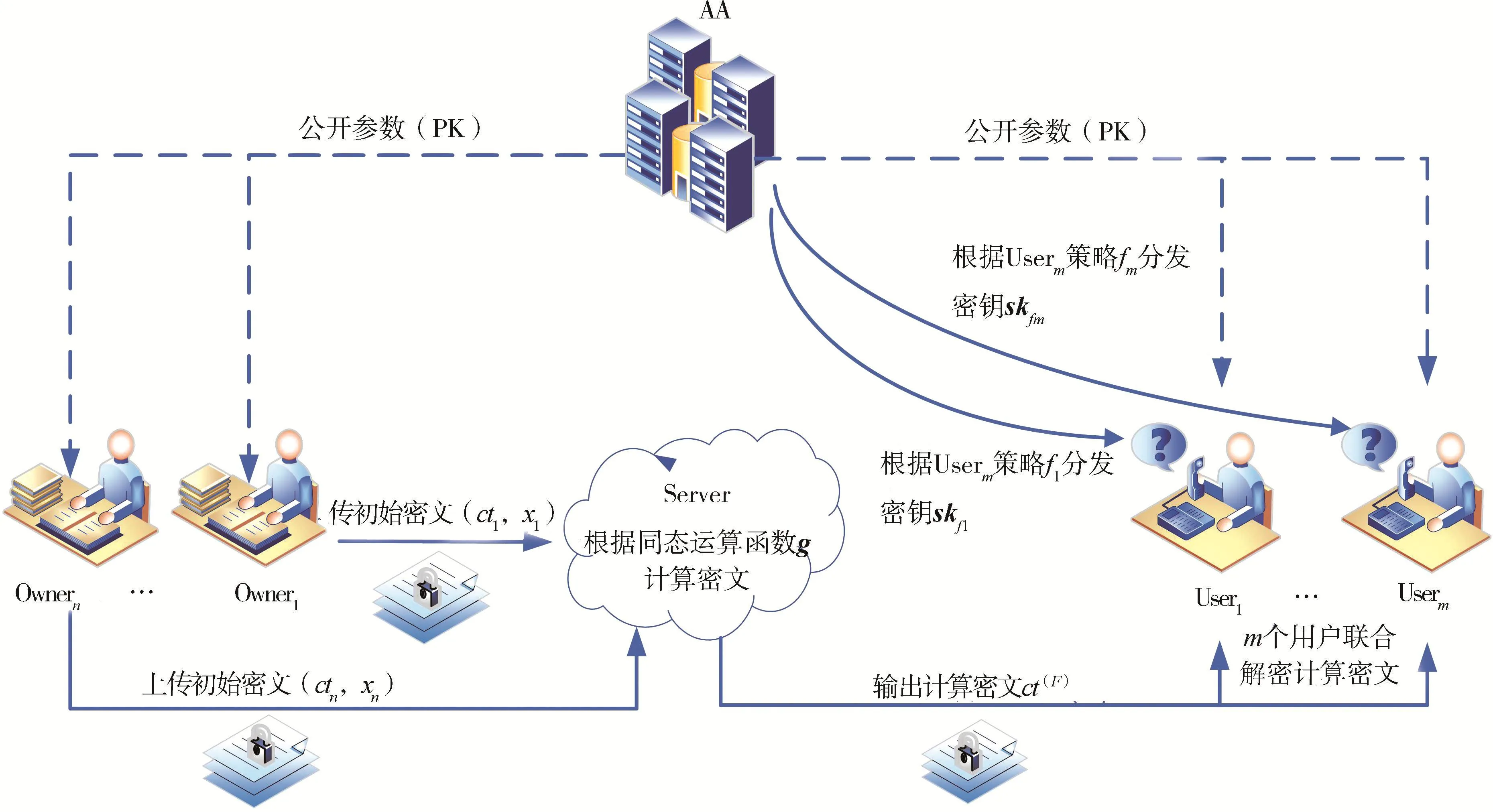
图1 应用场景模型

输出公共参数pp＝（A，B0，B，Bx，v，H），主密钥以下算法都默认以pp为输入。

KeyGen密钥生成算法由AA运行，根据主密钥msk和每个访问者（User）的访问策略f生成用户密钥skf和公开拓展密钥ek，具体过程如下：

（1）生成用户密钥skf

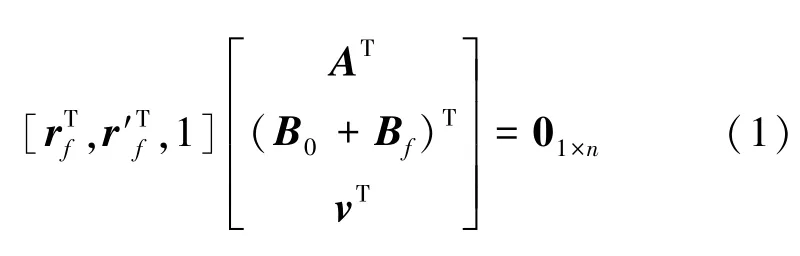
（2）生成拓展密钥ek

A′R＋（Im＋N＋1⊗tf⊗g）（误差为mB）。其次，对于每个选 取计算并且设置选取S（1），计算

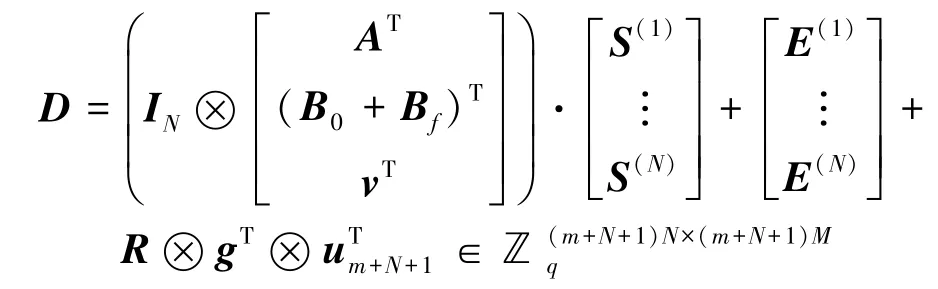
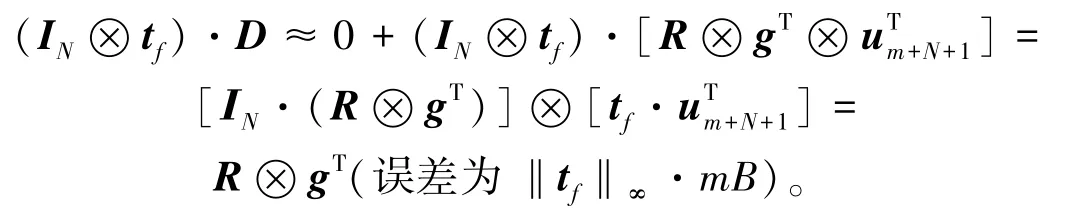
最终输出用户私钥skf＝rf以及公开的拓展密钥ek＝（P，D）。

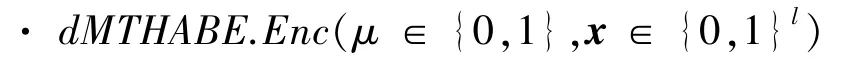
Enc加密算法由数据提供者（Owner）运行，根据明文μ和属性集x生成原始密文，并将密文上传到云服务器（Server），具体过程如下：

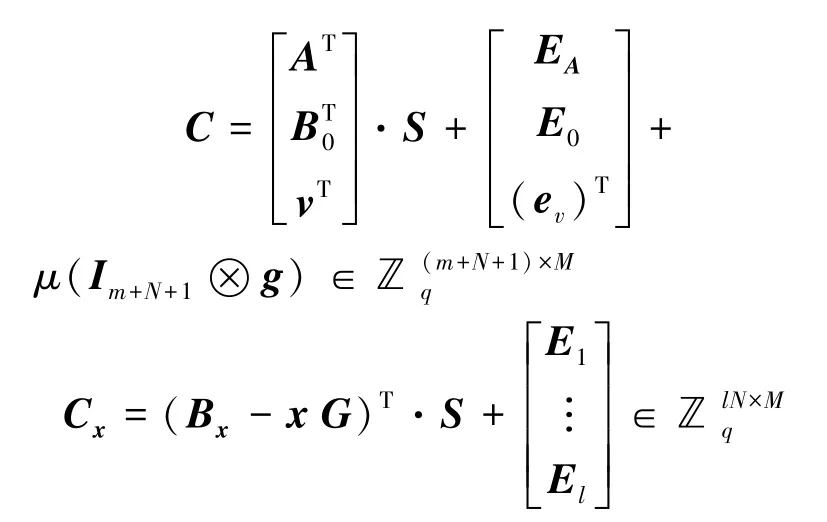
输出原始密文ct＝（x，C，Cx）。

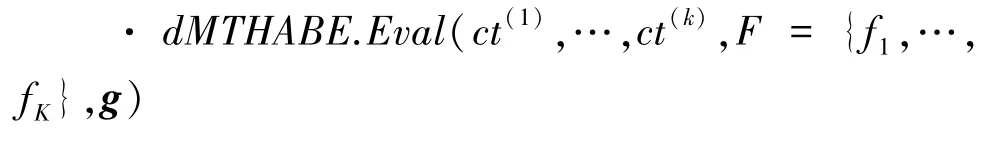
Eval同态计算算法由Server运行，根据多个Owner上传的原始密文、访问策略集F和同态运算函数g生成同态密文ct（F）， 且对于每个i∈［k］， 都存在fj满足fj（xi）＝0，具体过程如下：

（1） 采用推论 1 中EvRelation（f，x，Bx） 算法得到矩阵H，令并且计算

则对于访问策略fj对应的私钥rfj，令满足

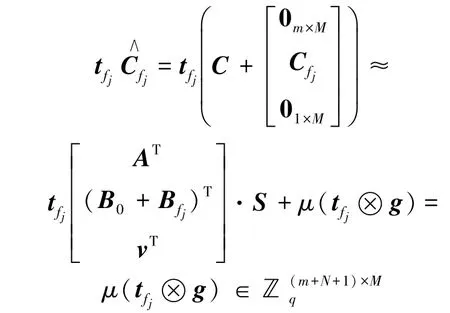
得到fj评估密文

（2）再对这些处理过的评估密文同态计算g函数，输出最终同态密文ct（F）。 且当同态密文再次进行同态运算时，需将同态密文先进行密文扩展，详细过程见3.2节。

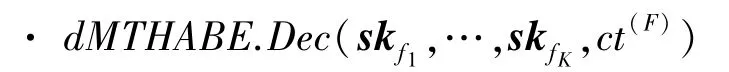
Dec解密算法由多个User联合解密，对于F＝｛f1，…，fK｝中的每个访问策略，给定密钥skf1，…，skfK和同态密文对于每个j∈ ［K］，有不同的则有私钥具体过程如下：

3.2 密文扩展

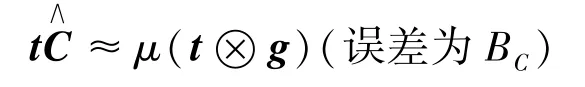
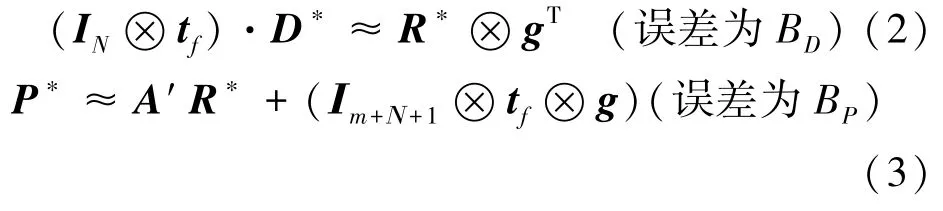
密文C′扩展具体过程如下。

计算

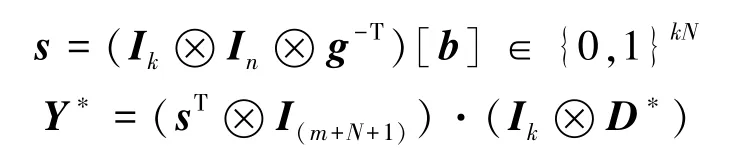
最终生成

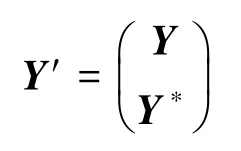
3.3 同态计算

设密文组ct1＝C1，ct2＝C2分别对明文μ1，μ2∈｛0，1｝ 加密，对应的随机矩阵为R1，R2以及对应的私钥为

（1）同态加法

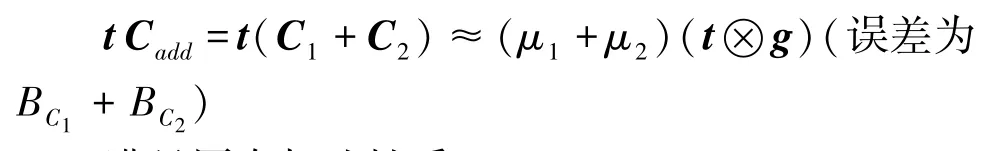
满足同态加法性质。

（2）同态乘法

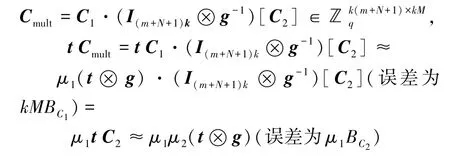
满足同态乘法性质。

3.4 密文扩展的正确性分析

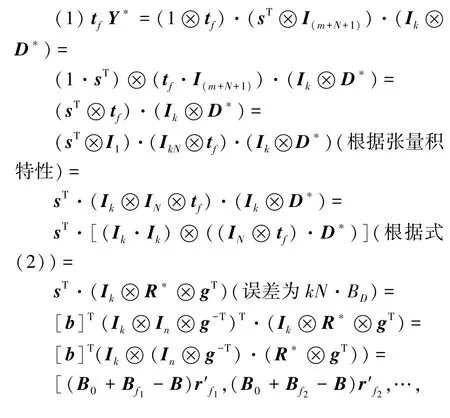
正确性分析完毕。

4 方案分析

4.1 参数设置

DLWE参数n，q，l根据决定方案的正确性和安全性的条件进行选取。

需要设置n≥λ和q≤ 2n，且设置l，K＝ploy（λ）。 当同态评估仅由NAND门组成的深度为dG的电路，且在最大深度为dF的K个不同策略下估算最坏情况下的噪声增长。本文定义Eval和KeyGen算法输出的密文C和扩展密钥（P，D）的最大误差为Bmax，即Bmax＝max（BC，BP，BD）。 从第 3节可知，对于某些多项式poly（·），当评估一个NAND门生成密文的噪声最大为

同样从第3节可知，对于某些多项式poly′（·），密文扩展算法生成的扩展密文的噪声最大为

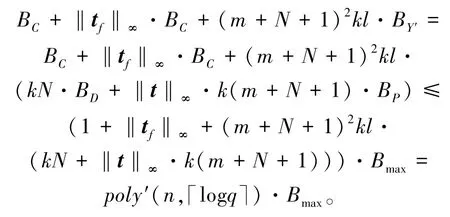
因为评估密文的最大噪声Bmax最大为

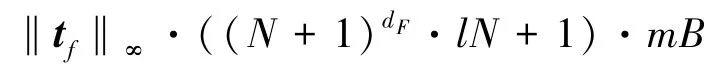
因此在K个不同的策略下同态计算深度为dG的电路生成的同态计算密文的噪声最大为

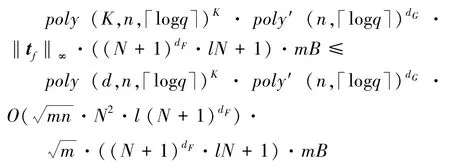
为了保证方案的正确性和安全性，本文选取参数使得在0＜ε＜1的情况下，以上数量的8倍小于2nε。 为 了 保 持 这 点， 本 文 设 置n＝以及选取q和χ，使之满足其中B是噪声分布χ的上限。选取这些参数会导致DLWEn，q，χ问题减少到n维晶格上的一个短向量近似为的因子。

4.2 安全性分析

本文方案的安全性依赖于底层的T⁃HABE安全模型，通过一系列假设，可以证明本文方案在决策性LWE问题下是IND⁃CPA安全的，即任何多项式时间的攻击者打破底层的T⁃HABE方案的 IND⁃CPA安全性是可以忽略的。证明如下：

与T⁃HABE方案中方式相似，通过考虑挑战密文ct＝（x，C，Cx）中列向量的不可区分性来证明安全性，设置x∗成为挑战属性。即考虑给攻击者以下向量

Game（0）。 此游戏和column游戏相同，所以有

Game（1）。 与Game（0） 相比，不同之处在于公钥参数B0，Bx＝［B1，…，Bl］的生成方式，并且有分布均匀的随机矩阵满足在这个游戏里，有来代替随机均匀选取这些矩阵。通过剩余哈希定理，得知的分布和均匀在上选取的是不可区分的，因 此 有

Game（2）。 与Game（1） 相比，不同之处在于改变了矩阵的分布，即均匀选取矩阵通过定理 1可知，Game（2） 和Game（1） 得到的矩阵是不可区分的，因此有

Game（3）。 与Game（2） 相比，不同之处在于密钥生成时，不使用陷门不失一般性情况下，对于挑战属性x∗，访问策略f，满足f（x∗）＝1。 采用H（A，f） 算法得到计算得根据EvRelation算法得到矩阵H，则有因此有

通过定理2，当给定R0，R和H，对于任意τ≥可 从中采样，其中通过生成通过定理 2，可知的边缘分布在统计上与 ｛0，1｝N上的均匀分布不可区分，并且条件下的概率分布是整数格上适当陪集上的离散高斯分布。由于这个游戏中攻击者得到的分布在统计上与Game（2）中的无法区分，所以有

Game（4）。 除了选择A的方式外，此游戏与Game（3） 相同。 挑战者从中选择随机A，而不是使用TrapGen生成。根据定理1，TrapGen生成的矩阵A的分布在统计上与上的均匀分布不可区分，所以有

Game（5）。 与Game（4） 相比，不同之处在于生成P和D的方式不同，挑战者随机均匀选取P∈而不是使用

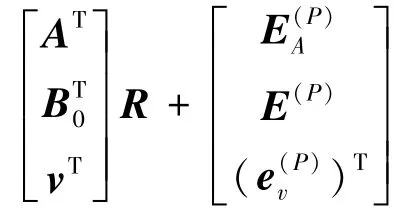
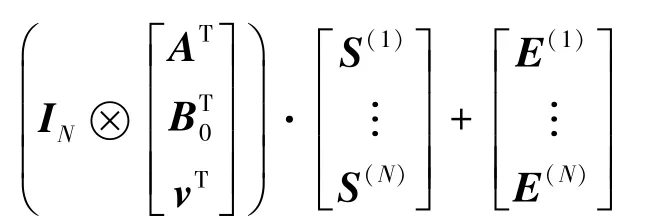
生成，由定理 1可知，Game（4）中P和D与Game（5）中的在统计上的均匀分布不可区分，所以

Game（6）。 与Game（5） 相比，改变了挑战密文的生成，令之后挑战密文可以被重写成

这与Game（5）中的密文

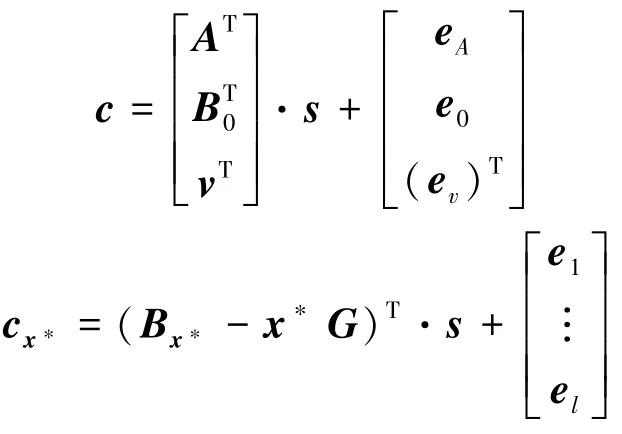
Game（7）。 与Game（6） 相比，改变uA和uv的分布到均匀分布，通过DLWEn，q，χ假设，这个改变不能 被 攻 击 者 区 分，所 以 有通过一系列游戏，有而在这轮游戏中，攻击者的优势为 0，也就是有因此本文方案dMTHABE是IND⁃CPA的。

4.3 性能分析

下面首先对本文dMTHABE方案与文献［8－10］中的多密钥方案进行性能比较，结果如表1所示。2016年，Peikert等在文献［10］中提出了两种动态多跳的MKFHE方案，任何参与方都可以实时、动态地加入到密文运算的过程中。其中方案一的特点为密文尺寸较大，而方案二密文相对较短，密文扩展实现较为方便。但该方案是基于公钥，不是属性基加密。Brakerski等在文献［8］中分别提出了单策略和多策略同态ABE方案，其中多策略方案可对满足不同策略的密文进行同态运算，但该方案是单跳的，不具备多跳性质，即同态计算过的密文不能再次与新密文进行同态计算。 2017 年，Hiromasa 等［9］在文献［10］的多跳MKFHE方案一的基础上，提出了具有动态同态计算的多策略同态ABE方案，但该方案和文献［10］的方案一具有相同的密文尺寸较大，密文计算效率不高的特点。而本文是在文献［10］的方案二基础上，提出的具有动态同态计算的多策略同态ABE方案，具有密文短，密文扩展方便以及同态计算效率高的优点。

下面将从私钥大小、原始密文大小、评估密文以及扩展同态计算密文大小（注：所有参数比较的都是位大小）方面，将本文方案与文献［8－10］中的多密钥方案进行对比。比较结果如表2所示。其中，l为访问策略的输入属性最大数量，n为LWE问题的维数，k为同态计算相关密钥或策略的数量，设其上限为K。dG和dF分别代表同态操作和访问策略电路的最大深度，

表1 方案性能比较

表2 方案的密钥和密文大小比较

从对比分析结果可知：与文献［10］中的多密钥全同态方案相比，本文方案将属性加密与多跳多密钥同态加密方案结合，引入了属性向量和访问策略，既实现了跨属性间的密文同态计算，又满足密文的细粒度的访问控制，并且满足多策略需求，可以满足大部分实际应用场景。与文献［8］中的多策略属性基同态加密方案相比，本文方案实现了多跳的功能，允许新密文直接参与同态计算，且密文尺寸较小。与文献［9］中方案相比，本文方案具有更小的密文，加解密开销变小，并且同态计算复杂度降低，密文只与一个部分有关，因此有着更高的计算效率。

5 结束语

本文提出一个基于LWE问题的支持多跳多策略和短密文的属性基全同态加密方案，短密文不仅可以减少通信开销，还可以减少加密、解密和同态计算的运行时间，有着更高的效率，并且证明了方案在选择属性下为IND⁃CPA安全。与以往方案相比，本文方案可以实现跨属性密文间的同态计算，满足云环境下多用户的需求，有着更灵活的访问控制，但本方案进行密文扩展时需要扩展密钥，这导致本文只能实现弱属性同态。下一步工作中，考虑对其进行优化，实现无需扩展密钥的多策略属性基全同态加密。另外本文的访问策略是布尔电路，下步工作要提出基于更灵活访问控制策略的多策略属性基全同态加密方案，以提高访问控制的灵活性。