基于模糊数学的通信网络密文信息差错恢复

刘淑芬，张 程

(华东交通大学理工学院，江西 南昌 300100)

1 引言

通信网络早已成为人们生活的一部分，且渗透至各个领域。与此同时，信息的安全性也受到各个领域专家的关注，并研究出相应的密文，保障通信网络信息安全。然而，通信网络不可避免地，总会出现各种人为或非人为因素，导致的不可预知差错，影响通信网络中，使用密文保护安全的信息，消失在通信网络中[1-2]。因此，国内外众多专家学者，都在研究密文信息的恢复方法。目前，国内外对于数据恢复的研究，将数据需要恢复的原因，分为数据丢失恢复、数据故障、数据缺失等，并从这几个方面，恢复数据[3-4]。

面对数据丢失问题，当前主要的数据恢复方法为数据重构，采用K-Nearest Neighbors(KNN)算法、压缩感知、非参数的数据自适应的插值算法、全局逐步细化插值算法等方式，恢复丢失的数据，此外，还有数据丢失模型，但是该种方法研究较少，尚未出现系统研究；故障数据的恢复，多采用调度失效流量至正常链路和提前部署备用方案两种策略，恢复故障数据；缺失数据的恢复，则引入了基于Armijo规则约束、基于LS-SVM、KNN算法等，恢复缺失的数据[5～7]。

但是，在上述的研究中，数据恢复方法，依然存在通信网络节点能耗高、数据恢复精度低等问题，为此采用模糊数学理论，建立通信网络密文信息恢复因素集，提高数据恢复精度，降低通信网络节点能耗。为此提出基于模糊数学的通信网络密文信息差错恢复。

2 研究基于模糊数学的通信网络密文信息差错恢复方法

2.1 设计密文信息恢复流程

此次研究通信网络密文信息差错恢复方法，需要利用模糊数学理论，增强密文信息特征，降低密文信息恢复难度，采用压缩感知算法，感知通信网络密文信息存在的差错，其密文信息恢复流程，如图1所示。

图1 密文信息恢复流程

从图1中可以看出，此次设计的密文信息恢复流程，需要增强输入的密文信息，感知密文信息存在的差错，对发现的密文信息存在的差错，从时间域和空间域恢复密文信息。

2.2 基于模糊数学增强密文信息

基于图1所示的密文信息恢复流程，采用模糊数学理论，增强输入的密文信息特征，需要计算数学模糊理论的增强算子。为此，假设密文信息X的大小为M*N，密度为L，则其在数学模糊域的隶属度函数为

(1)

式(1)表示把该密文信息，从通信网络中，变换到数学模糊域的过程。(1)式中，F2表示隶属度函数的指数模糊参数；F1表示隶属度函数的倒数模糊参数；T表示变换函数；xij表示位于第i行第j列的密文信息；T(xij)表示关于xij的变换函数；μij表示密文信息xij在数学模糊域的隶属度[8]。

经过式(1)转换后，得到的数学模糊域密文信息如下

(2)

式(2)中，μij(xij)表示密文信息xij对于密文信息密度L-1的隶属度。其阈值γ为：γ=T(υ)=0.5，其中，υ表示渡越点，且υ∈{xij|i=1，2，…，M;j=1，2，…，N}[9]。此时，可以确定隶属度函数的倒数模糊参数F1大小为

(3)

根据式(3)，即可得到隶属度函数倒数模糊参数F1的值。由于指数模糊参数值，通常取2[10]。所以，在此次研究中，隶属度函数指数模糊参数，F2=2。

根据上述内容，将密文信息变换到数学模糊域后，采用隶属度变换函数，对密文信息进行增强处理，则有

Ir(μij)=I1(Ir-1(μij))

(4)

式(4)中，r表示迭代次数，取正整数；I表示增强算子；I1表示迭代次数为1时的增强算子；Ir(μij)表示迭代次数为r时，对数学模糊域隶属度μij中的密文信息xij的增强[11]。此时，将增强后的数学模糊域密文信息，采用逆变换函数，变换回通信网络空间域，则有

(5)

式(5)中，I-1表示逆变换；zij表示变换回通信网络空间域的密文信息[12]。根据上述内容，即完成通信网络中，存在差错的密文信息增强过程，此时，需要感知密文信息存在的差错，并恢复存在差错的密文信息。

2.3 恢复通信网络密文信息

根据图1所示的密文信息恢复流程，采用压缩感知算法，感知密文信息存在的差错问题，从时间域和空间域恢复密文信息存在的差错问题。由于密文信息出现差错后的恢复过程，属于逆过程。基于(5)式得到的，变换回通信网络空间域的密文信息Z，且Z∈zij，需要求取，即密文信息Z中，存在的差错信息，则有

(6)

(7)

此时，在(7)式中，加入空间算子ξ和时间算子ψ，则有：

(8)

(9)

根据(9)式，可以得到R的解，此时，L就可以根据固定的R，就可以得到相应的解。重复运算(9)式，直至得到最优的R和L解，当R和L迭代收敛后，即完成密文信息的恢复。

将上述2.2节和2.3节的计算过程，代入图1所示的密文信息恢复流程中，即完成通信网络密文信息的恢复。

3 实验论证分析

此次研究的通信网络密文信息差错恢复方法，采用对比实验的方式，验证恢复通信网络密文信息差错问题效果。此次实验，采用Berkeley网络模拟器，模拟通信网络。选择Abilene和GEANT两个数据集，作为此次实验的密文信息。将此次研究的通信网络密文信息差错恢复方法，记为实验A组，两组传统的通信网络密文信息差错恢复方法，分别记为实验B组和实验C组。确定网络数据测量时间，改变密文信息丢失率、迭代次数和发送带宽，对比三组方法密文信息恢复误差、收敛趋势和时间。

3.1 实验准备

此次实验选择的Abilene和GEANT两个数据集，其中Abilene数据集，具有12个节点，144个节点对，该数据集的采样天数为168天，每五分钟采样一次；GEANT数据集，具有23个节点，529个节点对，该数据集的采样天数为112天，每15分钟采样一次。

基于此次实验，选择的实验对象，采用Berkeley网络模拟器，模拟通信网络的拓扑结构，如图2所示。

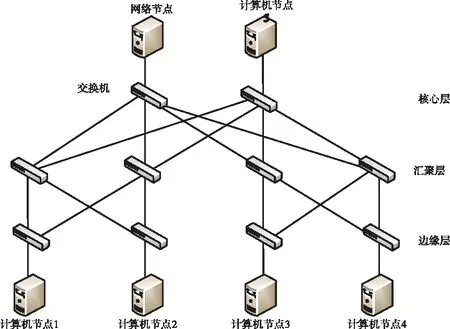
图2 通信网络的拓扑结构

从图2中可以看出，此次采用采用Berkeley网络模拟器，模拟通信网络的拓扑结构，共使用了10台OpenFlow交换机，作为通信网络拓扑结构控制节点，5台服务器，作为计算机节点群，1台服务器作为通信网络节点。

由于此次实验，将选择建立虚拟通信网络，模拟实验的方式，验证此次研究的通信网络密文信息差错恢复方法，所以，为图2所示的通信网络的拓扑结构中的1～4计算机节点，每个节点都申请7台虚拟机，共计28台虚拟机，为同一个虚拟通信网络服务。

基于上述内容，采用Berkeley网络模拟器，设置的通信网络拓扑结构，所需要的实验环境，如表1所示。

表1 通信网络拓扑结构实验环境

表1中的Iperf网络测试工具，可以通过发送密文信息，测试通信网络密文信息的丢包、带宽、抖动等参数，确定通信网络运行状态，模拟通信网络中，制定带宽的数据流，从而保证实验结果的严谨性。

基于上述内容，选择的实验对象，设置的实验环境，采用三组方法，分别恢复通信网络密文信息，验证通信网络密文信息差错恢复方法，恢复通信网络密文信息，恢复效果。

3.2 丢失差错下密文信息恢复误差对比

基于此次实验，设置的实验参数，在密文信息出现丢失差错时，对比三组方法，恢复通信网络密文误差。在本组实验中，将密文信息丢失率设定在10%～90%之间，对比三组方法，恢复不同丢失概率的密文信息，所产生的恢复误差，且误差随着丢失密文信息的丢失率增加而提高。其实验结果，如图3所示。

图3 丢失差错下密文信息恢复误差对比图

从图3中可以看出，随着密文信息丢失概率的增加，三组方法恢复密文信息误差，都出现了不同程度的增加，其中，实验C组密文信息恢复误差，较实验A组密文信息恢复误差，增加了52%；实验B组密文信息恢复误差，较实验A组密文信息恢复误差，增加了30%。由此可见，此次研究的通信网络密文信息差错恢复方法，恢复通信网络中，存在的密文信息丢失差错，具有较低的密文信息恢复误差。

3.3 密文信息恢复收敛趋势

基于第一组实验结果，进行第二组实验，采用均方根误差，判断三组恢复方法，随着迭代次数的变化，恢复通信网络中，存在丢失差错的密文信息的收敛速度，其网络的测量速率场景如下：通信网络在同一天的速率测量中，是相同的。基于上述确定的通信网络速率测量时间，均方根误差计算公式如下

(10)

将此次实验选择的两组数据集的采样率，即虚拟通信网络中，使用的数据占采样数据中的比重，设为50%，采用(10)式，计算三组方法，在不同的迭代次数下，恢复通信网络密文信息，均方根误差的收敛速度。其实验结果如图4所示。

图4 收敛速度对比图

从图4中可以看出，随着迭代次数的增加，均方根误差在不断地减小，并迅速收敛到一个稳定值；其中，实验C组恢复通信网络密文信息，其均方根误差达到稳定性速度是三组方法中最快的，但是，均方根误差和收敛速度，是三组实验中最大和最慢的；实验B组恢复通信网络密文信息，其均方根误差达到稳定性的速度，是三组方法中最慢的；只有实验A组，均方根误差、稳定速度和均方根误差达到稳定性，都优于实验B组和实验C组。这说明本文所研究的通信网络密文信息错误恢复方法，恢复速度快，且均方根误差能达到稳定速度。

3.4 密文信息恢复时间对比

基于第一组和第二组实验结果，进行第三组实验对比三组方法，恢复通信网络中的密文信息时间。通信网络密文信息出现差错后，其密文信息的总恢复时间，包括密文信息差错检测时间t1、恢复处理时间t2和恢复生效时间t3，则密文信息的总恢复时间为t=t1+t2+t3。为获取精确的密文信息恢复时间，在本组实验中，改变通信网络的发送带宽，记录密文信息差错检测时间、恢复处理时间和恢复生效时间，计算总恢复时间，其实验对比结果，如表2所示。

表2 密文信息回复时间对比表

从表2中可以看出，三组方法，恢复密文信息，当发送带宽增加至400 Mbps时，已经不会影响密文信息恢复速度。其中，实验A组恢复通信网络密文信息，其信息恢复速度，明显比实验B组快50.6ms，比实验C组快50.6ms。由此可见，此次研究的通信网络密文信息差错恢复方法，恢复通信网络密文信息，所需时间短，具有较快的恢复速度。

综合上述三组实验结果可知，此次研究的通信网络密文信息差错恢复方法，恢复通信网络密文信息，收敛速度快，所需时间短，具有较低的密文信息恢复误差、稳定性的均方根误差和恢复误差、较快的恢复速度。

4 结束语

此次研究通信网络密文信息差错恢复方法，充分利用模糊数学技术，通过数学计量方式，增强通信网络密文信息特征，降低密文信息恢复误差。但是，此次研究的通信网络密文信息差错恢复方法，未曾考虑通信网络变化，对密文信息恢复的影响。因此在今后的研究中，还需深入研究通信网络密文信息差错恢复方法，需要恢复的密文信息，所处通信网络变化参数，判断通信网络对密文信息的影响，进一步提高通信网络密文信息差错恢复精度。