2-CPR/UPU三平移并联机构运动学分析与优化设计

2022-10-21李丽红张发海

机械传动 2022年10期

李丽红张发海朱磊

（1 江苏安全技术职业学院机械工程学院，江苏徐州 221000）

（2 中国矿业大学材料与物理学院，江苏徐州 221116）

0 引言

空间三平移并联机器人机构具有结构刚度大、控制精度高、承载能力强等优点而被广泛应用于工业包装、航空航天、3D 打印等领域[1]。Vischer 等[2]最早提出三平移DELTA 机构；Tsai等[3]提出一种空间三平移并联机构，其支链由平行四边形机构、移动副构成。此外，还有一些学者研究了通过DELTA 机构衍生出的三平移并联机构[4]。以上机构都有耦合度大于等于1 的特点，这也使得机构不具有运动解耦特性，直接导致三平移机构动力学分析、运动规划与控制分析过程十分复杂。

目前，解耦空间三平移并联机器人机构的设计与研究成为国内外学者关注和研究的热点[5]。毛玺等[6]设计了一种支链完全对称分布且零耦合度的三维纯平移并联机器人机构，并根据螺旋理论方法对运动输出特性进行了计算；建立运动学方程并得到机构的位置解、速度、加速度等运动学分析；通过Matlab 和SolidWorks 联合仿真得到样机的位移、速度、加速度等参数所对应的运动规律曲线图；在此基础上，研究得到位置工作空间及其奇异性特征。季晔[7]设计了一种弱耦合且无奇异的三平移并联机构，通过螺旋理论和Kutzbach-Grubler 公式推导验证了机构运动性质；建立约束方程并得到运动学位置方程解析式，根据雅可比矩阵分析得到机构无奇异位置特征；根据五次多项式对机构动平台参考点进行了轨迹规划。程刚等[8]根据方位特征集拓扑结构设计理论，阐述了并联机构解耦特性分析过程，提出一种零耦合度的三平移并联机构；该机构具有结构简单、位置正逆解分析容易等特点，为该并联机构实现高精度位置控制提供了可能。沈惠平等[9]针对三平移并联机构运动控制及轨迹规划等较为复杂的问题，提出了一种具有解析式位置正解的三平移并联机构；计算出方位特征集为三平移、耦合度为0、自由度为3；推导了运动学方程位置解的符号解析式，分析操作空间和奇异性特征的性能；最后通过仿真分析运动规律，验证得到与理论计算一致的结果。曾达幸等[10]针对三平移并联机构的综合问题，通过螺旋理论阐述了移动副存在的条件，利用支链输入副的选择原则得到支链的运动副配置，综合出全局各向同性的三维移动解耦并联机构；并对该机构进行数学建模并完成了运动学位置分析；建立灵活性的目标函数完成位形优化，并进行了样机研制。朱伟等[11]提出了一种弱耦合且对称的三平移并联机构，其中，2条支链结构为RRPaR，另外一条支链结构为PPaP；计算了几种重要的拓扑结构特征，完成了数学方程模型的建立，并得到位置解（正解和逆解）的符号解析式。

考虑到强耦合三平移并联机构输出强耦合所引起的实时控制问题，本文中根据拓扑结构综合理论，提出一种耦合度为0 的新型2CPR/UPU 三平移并联机构，并对其进行了运动学分析和参数优化。

1 并联机构结构分析

1.1 机构设计

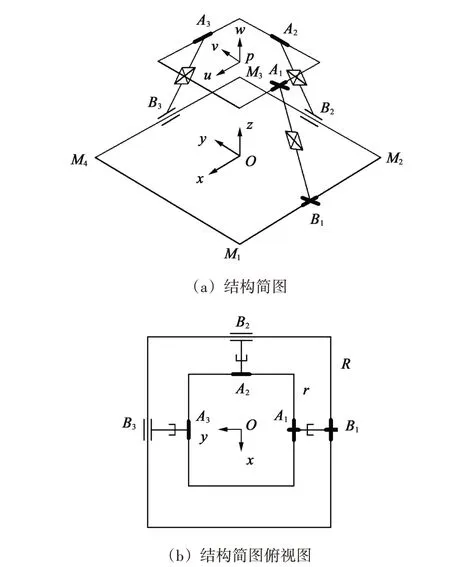
图1 2CUP-UPU并联机构结构简图Fig.1 Structural diagram of parallel mechanism of 2CUP/UPU

1.2 拓扑特性分析

并联机构自由度计算公式根据方位特征集拓扑结构综合理论进行计算[12]，具体定义为

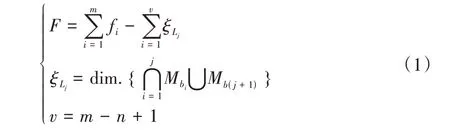
作为衡量并联机构复杂程度的耦合度指标，基本运动链的耦合度κ为

式中，mj为第j个SOCj的运动副数；Ij为第j个SOCj的驱动副数。

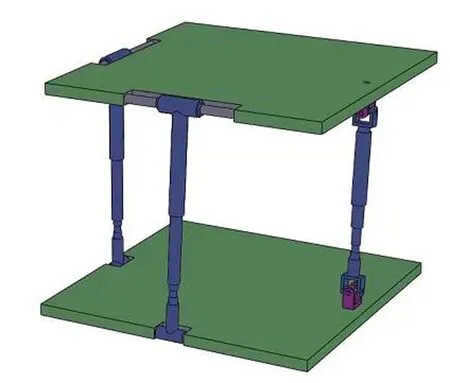
图2 2CPR/UPU并联机构三维模型Fig.2 3D model of 2CPR/UPU parallel mechanism

（1）根据机构结构简图和三维模型图，根据支链各运动副之间的布置特点，分析出支链对应的POC集Mbj分别为

式中，Mbj为支链j的方位特征集；t为移动特征；r为转动特征。

②支链2、支链3 的单开链为SOC{-Ci⊥Pi2//Ri3}，（i=2，3）计算得到支链的Mbj为

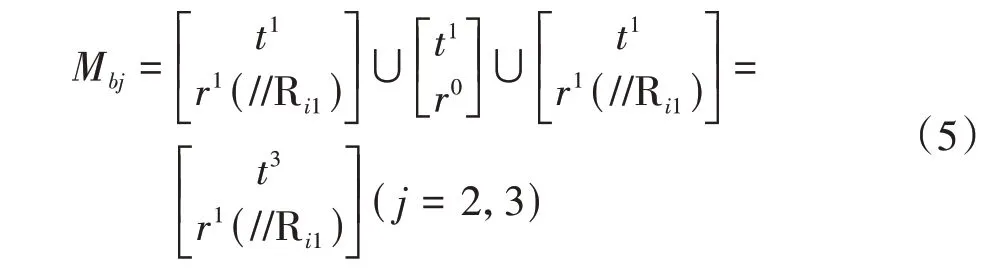
（2）分析第一条独立回路的位移方程，以第2支链、第3 支链构成第一个独立运动回路，根据

式（1），则回路1的位移方程ξLj为

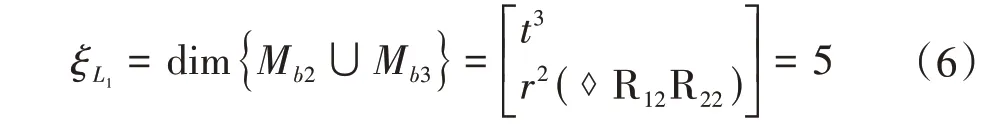
①计算第2支链、第3支链构成的子并联机构的POC集为

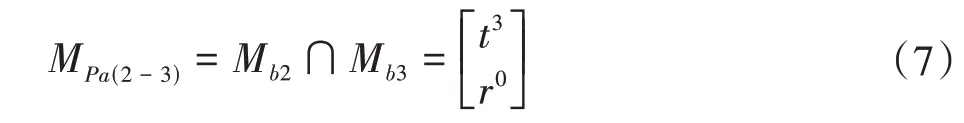
②将参数代入式（1），得到由支链2、支链3 组成的子并联机构的自由度F2-3为

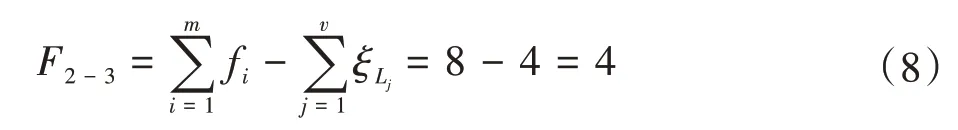
（3）分析第二条独立回路的位移方程拓扑特性，以回路1 与支链1 组成第二回路，将相关参数代入式（1），得到回路2的位移方程数ξL2，有

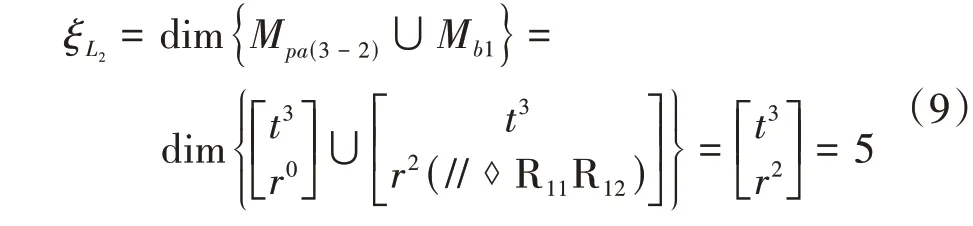
①并联机构的POC集Mpa(1-2-3)为

②得出机构自由度F1-2-3为

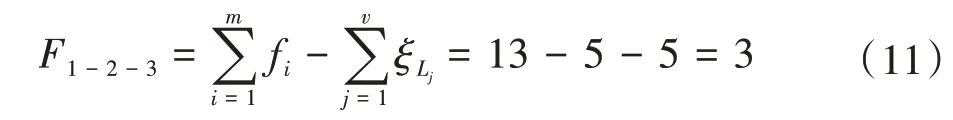
（4）约束度Δj分析，根据上述步骤代入式（3）中。计算过程为

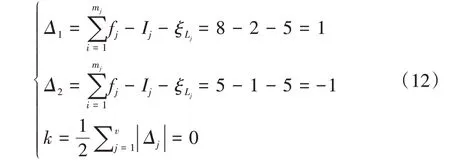
结果分析表明，2CPR/UPU 并联机构具有空间三维移动的运动特性，耦合度k为0，机构的运动学和动力学分析容易、实时控制精度高；另外，位置正解具有符号解。

2 机构的位置分析

2.1 位置逆解分析

机构位置逆解分析是指通过动平台位置输出得到输入的表达式的过程[13]。设定动平台位置中心P点坐标（x，y，z），即为动平台位置输出。将静坐标系{O-xyz}建立在静平台中心。

已知P点坐标（x，y，z），利用平移转换原理映射到Ai点在静坐标下的坐标点，即A1（x，y-r，z）、A2（x-r，y，z）、A3（x，y+r，z）。同样，可得到Ai点在静坐标下的坐标点B1（0，-R，0）、B2（-R，0，0）、B3（0，R，0）、M1（R，-R，0）、M2（-R，-R，0）、M3（-R，R，0）、M4（R，R，0）。

根据移动副的位移恒定为li，建立约束方程为

对于支链2、支链3 而言，B2和B3的位置不固定，通过向量之间的外积原理，推导得到的关系等式为

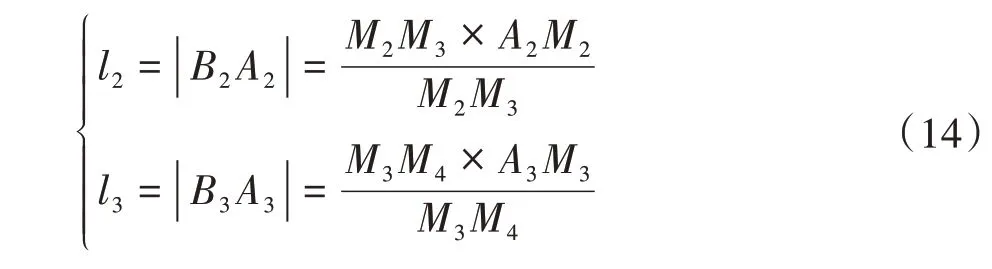
通过等式（13）和等式（14），得到运动约束方程为

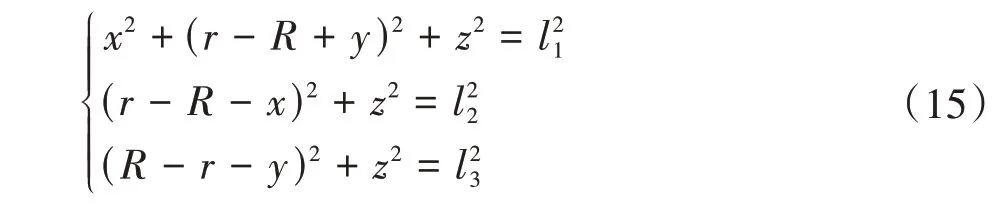
分离变量得到逆解表达式为

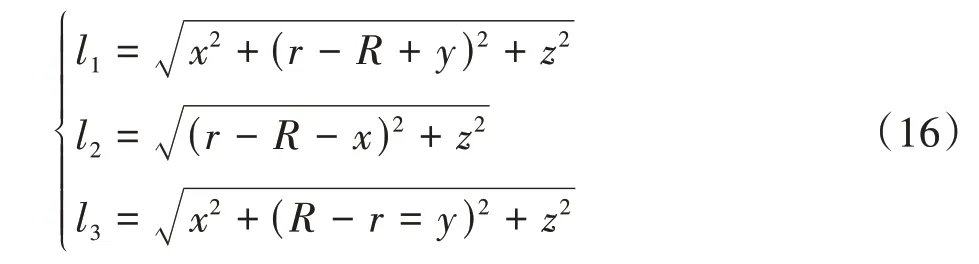
2.2 位置正解分析

位置正解分析是指已知移动副输入（l1，l2，l3）推导出动平台执行末端位置（x，y，z）的过程。利用等式（15）推导出运动学正解符号解析式为

3 奇异分析

3.1 机构雅可比矩阵

机构的输入l=（l1，l2，l3）T，所对应的速度l̇=(l̇1，l̇2，l̇3)T，动平台执行末端位移X=（x，y，z）T，执行末端速度可表示为=(vx，vy，vz)T。

同时，对等式（15）求导并分离变量，推导出机构正逆解雅可比矩阵。

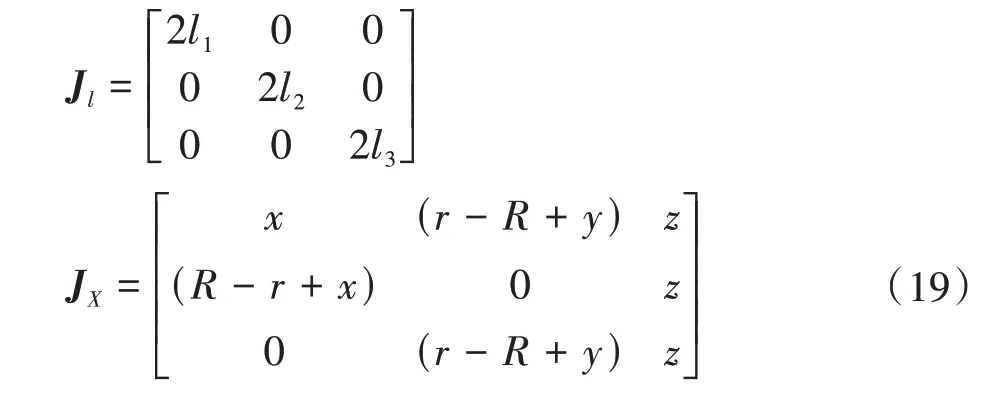
式中，Jl为逆雅可比矩阵；JX为正雅可比矩阵。

若JX非奇异，则

[76]Economic Survey of Burma, 1954, Rangoon: Superintendent, Union Govt Printing and Stationery, 1954, p.10.

若Jl非奇异，则

3.2 逆解奇异性分析

机构逆解奇异发生的条件为det(Jl)= 0 且要求det(JX)≠0。计算得到det(Jl)表达式为

det(Jq)= 8l1l2l3（22）

满足det(Jl) = 0 的条件有3 种情况，分别是支链1、支链2、支链3驱动副位移为0，当任意支链驱动副位移为0时，机构处于临界位置状态，该情况下会处于卡死状态。该情况也叫边界奇异。通过控制驱动副的移动范围可有效地解决该极限边界奇异发生。图3所示为逆解奇异。

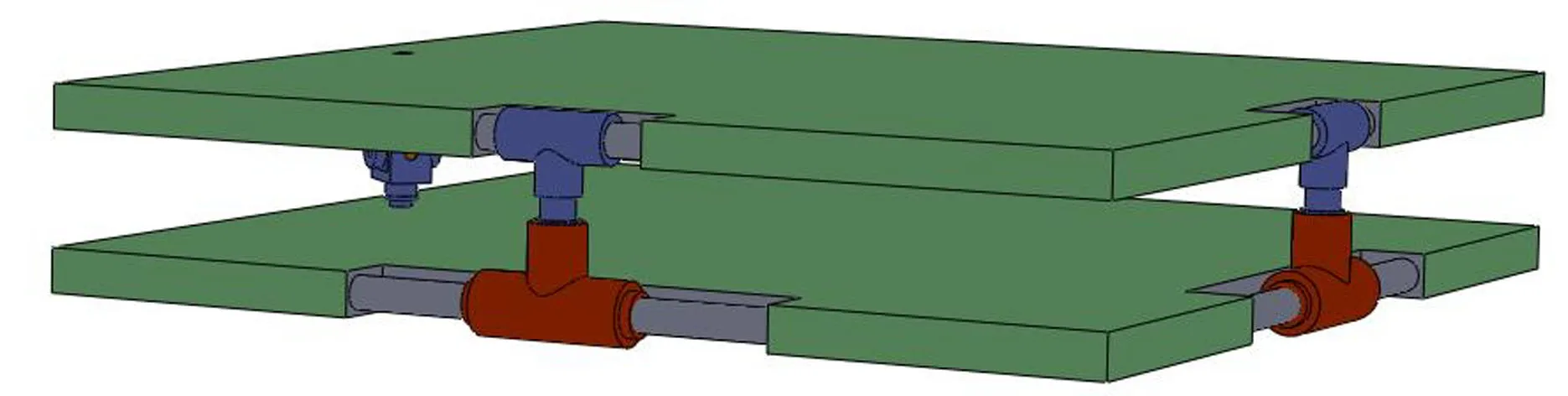
图3 逆解奇异情形Fig.3 Singular case of inverse solution

3.3 正解奇异性分析

机构正解奇异发生的条件为det(JX)= 0 且要求det(Jl)≠0。经推导计算得到det(JX)的表达式为

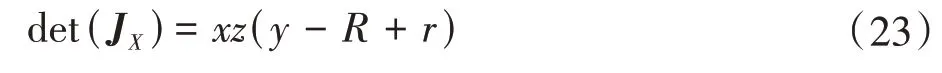
正解奇异出现条件为det(JX)= 0，即存在条件是x= 0或y=R-r或z= 0。

图4 正解奇异情形Fig.4 Singular case of positive solution

3.4 混合奇异性分析

机构混合奇异发生的条件为det(JX)= 0 且det(Jl)= 0，所有支链驱动副位移为0，则要求动静平台尺寸相同，即R=r。因此，混合奇异存在条件为{l1=l2=l3= 0，R=r}。此时，动静平台理论上重合才能出现该奇异。该奇异失去自由度，应当在设计过程避免出现。混合奇异如图5所示。

图5 混合奇异情形Fig.5 Mixed singular case

4 机构的工作空间分析

机构的运动范围主要受主动副运动范围、运动学逆解、转角干涉等约束条件所限制[14]。在仿真分析并联机构工作空间的过程中，需要结合这些约束条件，采用极值搜索法得到工作空间的边界，边界点内点的集合即搜索得到的工作空间图形。以表1中的算例参数值为例。

表1 机构的一组参数值Tab.1 A set of parameter values of the mechanism

由图6所示可知，工作空间形状呈半椭圆形，且工作空间边界位置光滑，并没有空洞，形状对称性较好；在x-o-y投影面关于y=0 对称分布，类似“伞状”分布；在y-o-z投影面完全关于y=0 对称分布，呈椭圆形状分布；在x-o-z投影面，形状类似椭圆形状，关于y=0.1对称，整个工作空间较大。

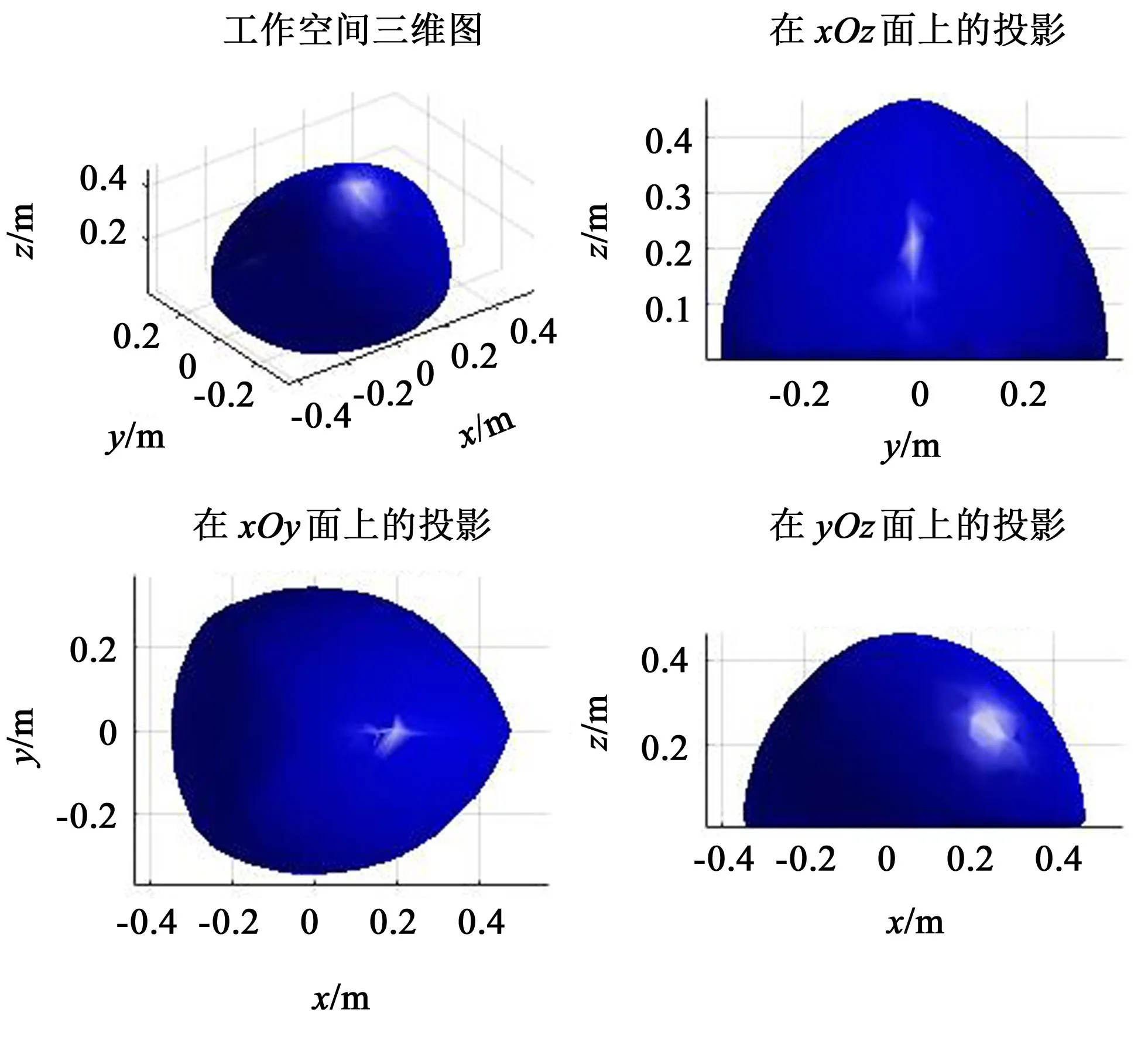
图6 工作空间三维图Fig.6 3D diagram of the mechanism workspace

5 并联机构运动灵巧性分析

灵巧度是一种评价并联机构运动过程中传递精度的性能指标。灵巧度越高，机构的各向同性越好[15]；一般根据运动学方程的雅可比矩阵进行计算分析。灵巧度具体定义为

当GCI= 0 或者接近0 时，所对应的雅可比矩阵为病态矩阵，机构的运动性能较差，输入输出之间的传递精度低；反之，当GCI= 1 或者接近1 时，机构的运动性能较好，且对应的输入输出的传递精度高，运动传递偏差小。利用上述定义公式，通过Matlab 软件，根据图7所示灵巧度在工作空间内的搜索流程，采用极坐标搜索法完成整个搜索过程，计算执行末端在操作空间内的运动灵巧度分布。

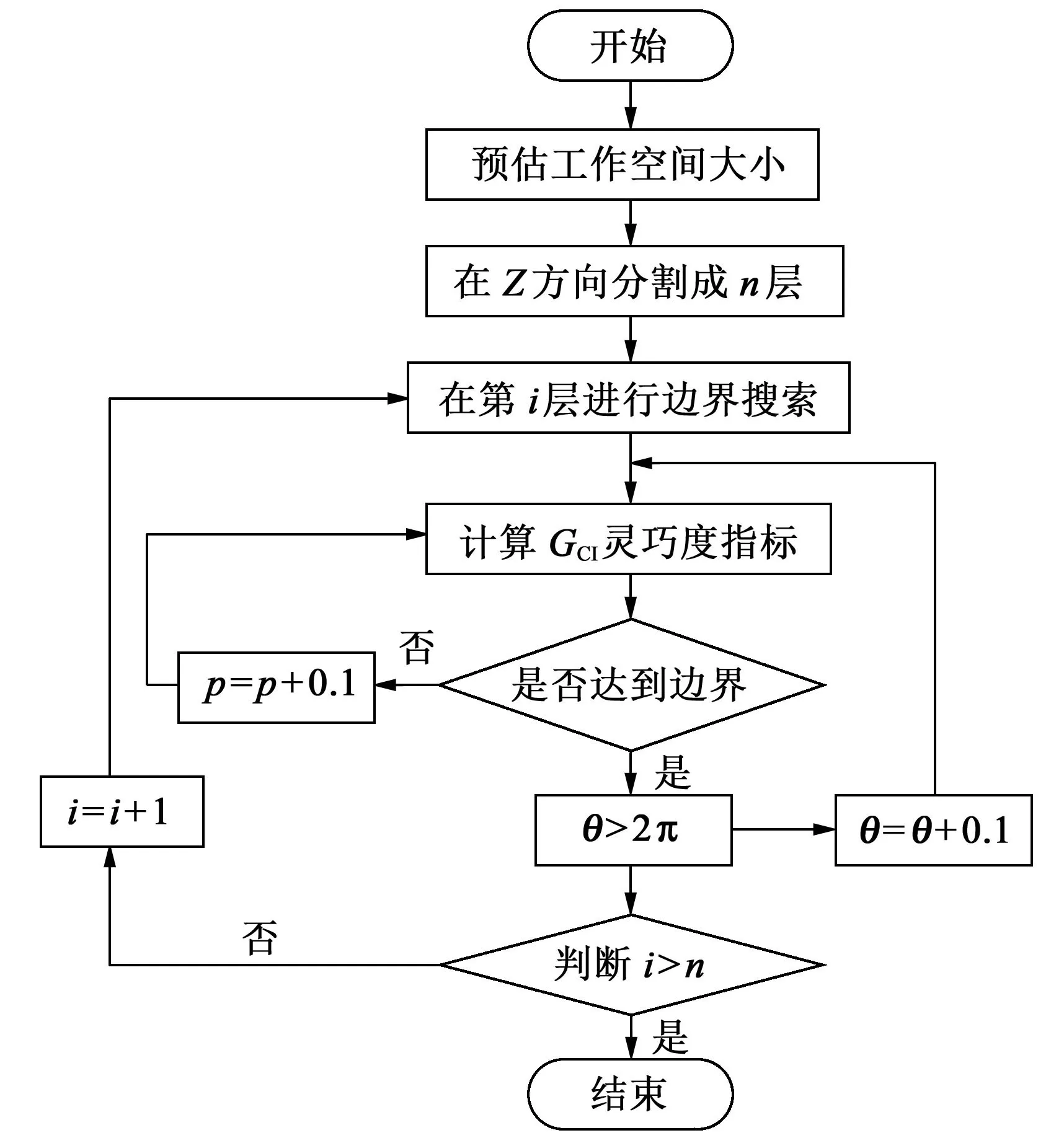
图7 运动灵巧度搜索流程图Fig.7 Flow chart of motion dexterity search

图8所示为机构在工作空间内灵巧度分布以及不同高度下灵巧度分布图。由图8中可知，工作空间表面的灵巧度分布均匀，当z=0 时，GCI= 0 或者接近0，机构的运动性能较差，输入输出之间传递精度差。z=0.1 m 时，运动性能由外向内越来越大，机构的传动精度越来越高，所对应的灵巧度在中间区域最大，最大值为0.75左右。z=0.2 m时，中间区域的灵巧度略高于边界区域的灵巧度，中间区域的灵巧度最高可达0.4左右。当z=0.3 m和z=0.4 m时，灵巧度不随位置而改变，所有的灵巧度相同，各位置分布均匀，传递性能一般，输入输出之间传递精度不高。

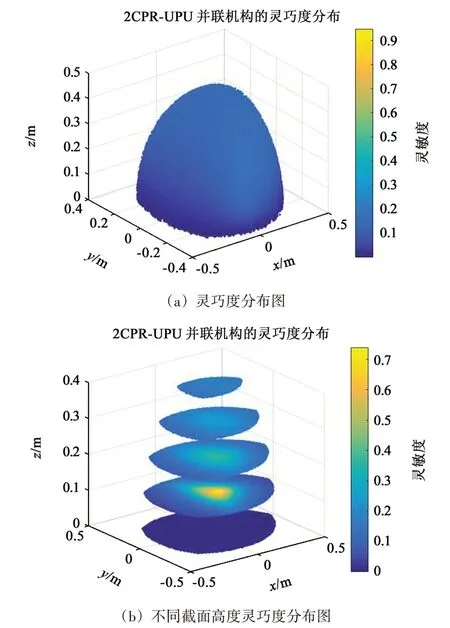
图8 运动灵巧度分布图Fig.8 Distribution of movement dexterity

6 尺度综合

6.1 优化模型建立

考虑到实际工程需求，期望获得更好的运动灵活性性能。可通过优化2CPR/UPU并联机构的几何设计变量来解决尺寸综合问题。建立目标函数以及给定结构参数约束范围分别为

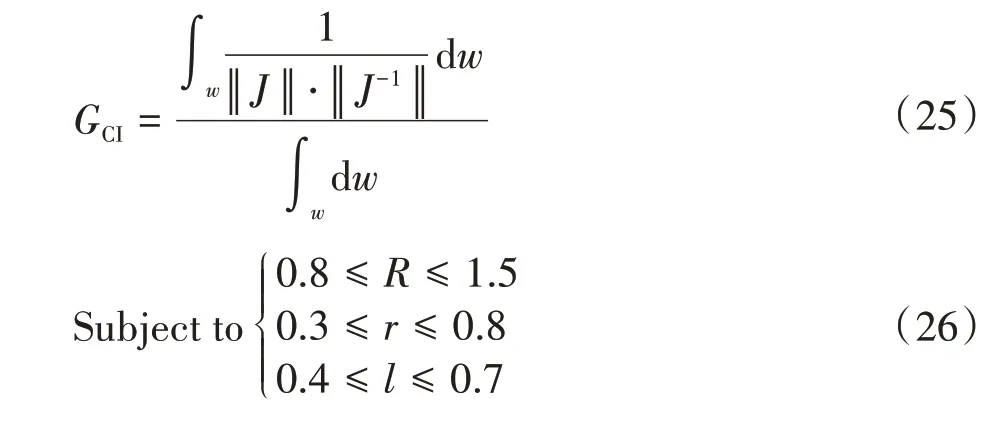
6.2 优化算法的选择

针对上述含有约束变量的单目标问题，选择一种模仿蝗虫在自然界的群集行为的蝗虫优化算法（Grasshopper optimization algorithm，GOA）[16]对目标函数进行优化设计。在求解未知搜索空间的实际问题时，GOA 算法在迭代过程中可搜索得到精确的全局最优值，具有迭代精度高、扩展性强、优化效率高的特点[17]。蝗虫优化算法的参数选取如表2所示。

表2 蝗虫优化算法参数Tab.2 Parameters of grasshopper optimization algorithm

根据Matlab 软件编程得到优化目标随迭代次数的变化图如图9 所示。目标函数在迭代次数为40 左右时趋于稳定，并稳定在0.374 2 左右。得到优化后的尺寸参数的最优值如表3所示。

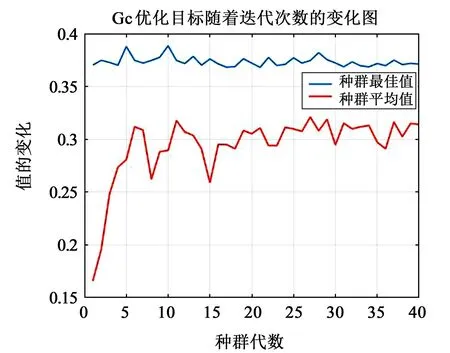
图9 优化目标随迭代次数变化图Fig.9 Variation of optimization objectives with iteration times

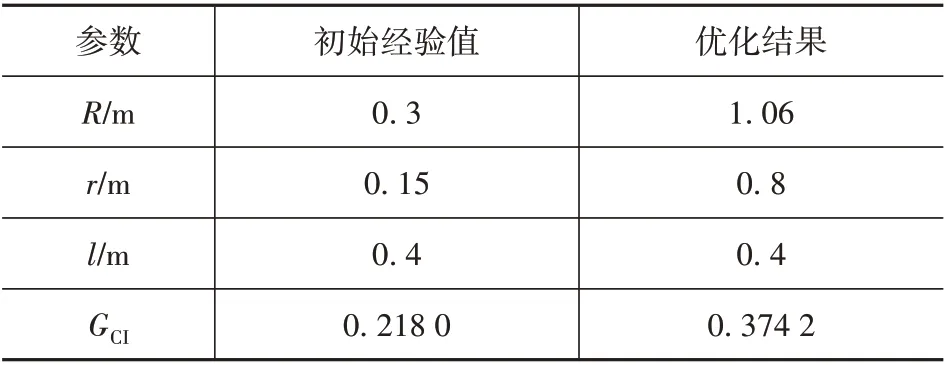
表3 2CUP/UPU并联机构参数值对比Tab.3 Comparison of parameter values of 2CUP-UPU parallel mechanism

6.3 优化算例分析

利用优化后的结构参数得到的灵巧度分布图如图10 所示。和之前的初始经验值相比，优化后的灵巧度得到显著提高，相比之前提升了将近1倍，性能得到大幅提升；优化后的机构灵巧度分布均匀，边界表面相比之前得到很大改善，且内部的灵巧度最大值最高可达1。此时的机构运动过程中，传递精度高，运动传递偏差小。结果表明，优化后的机构性能相对之前更加优越；算例分析结果也说明了算法的有效性和可靠性。