含过渡齿套鼓型齿联轴器的啮合力学特性分析

2022-10-21王孝义张志伟张国涛夏清华杨晓红李天超朱长江

机械传动 2022年10期

王孝义张志伟张国涛夏清华杨晓红李天超朱长江

（1 安徽工业大学机械工程学院，安徽马鞍山 243032）

（2 安徽泰尔重工股份有限公司，安徽马鞍山 243000）

0 引言

鼓型齿联轴器可承受较高转矩，具有径向、轴向和周向等轴线偏差补偿能力，被广泛应用于冶金、船舶和轨道交通等机械装备。在实际使用过程中，鼓型齿联轴器常需要在高速重载工况下运行，鼓型齿轮副作为鼓型齿联轴器的核心部件，其在复杂工况下的啮合力学特性对鼓型齿联轴器的传动特性和传动系统的平稳性具有重要影响。

迄今为止，国内外围绕鼓型齿轮副的啮合性能开展了大量研究。Guan 等[1]建立了由3 种不同加工方法进行修形的鼓型齿联轴器高精度有限元网格模型，采用有限元方法计算并对比了这3种模型下的齿面接触特性。周淳等[2]采用数控插补法加工鼓型齿齿面，降低了齿面粗糙度，提高了齿轮精度，使得鼓型齿联轴器的承载能力和使用寿命得到了较大提高。刘鹄然等[3-4]使用铣刀加工鼓型齿，进行齿面接触分析，并进行了试验验证。为进一步明晰鼓型齿轮副的接触特性，研究人员从不同工况参数和结构参数入手，对鼓型齿轮副接触特性的影响因素展开了探讨。方喜峰等[5]构造了不同位移圆半径的鼓型齿，分析了鼓型齿面的接触应力和动态特性。关亚彬等[6]采用有限元分析和响应面设计的方法，建立了最优位移圆半径和结构参数、工况参数之间的关系式。李锋等[7]基于鼓型齿联轴器有限元模型，分析了不同转速下鼓型齿联轴器的接触应力和等效应力。Keum[8]通过有限元方法研究了位移圆半径、齿数、模数的变化对鼓型齿联轴器齿面接触应力的影响规律。Raynald等[9]通过有限元法研究发现，鼓形齿的齿根弯曲应力和齿面接触应力受鼓形齿齿形参数的影响。朱文文等[10]分析了压力角、刀具位移圆半径和齿顶高系数对两轴线平行工况下的鼓形齿联轴器承载能力的影响。夏清华等[11]对GCL13 型鼓形齿联轴器在轴线对中和偏转两种工况下的力学性能进行了计算和分析。

随着现代冶金机械和船舶交通装备的不断发展，研发具有更高承载能力的鼓型齿联轴器成为重要的发展方向。传统鼓型齿轮副在工作过程中，鼓型齿轮的齿根断裂或齿面磨损胶合等不良接触状态频频发生，极大限制了鼓型齿联轴器在复杂工况下的应用。为改善鼓型齿轮副的啮合力学特性，本文中在传统鼓型齿轮副结构的基础上，设计了一种新型含过渡齿套的鼓型齿轮副结构。建立两种齿轮副结构的有限元模型，分析了鼓型齿轮副关键部位的啮合力学特性和不同倾角的影响。研究结果对于丰富鼓型齿联轴器的设计方法具有重要意义。

1 鼓型齿轮副的啮合力学模型

1.1 鼓型齿轮副结构及其啮合状态

如图1（a）所示，传统鼓型齿联轴器的鼓型齿轮副由一对内啮合的齿轮组成，分别是外齿轴套与内齿轴套，两齿轮齿数相等；其外齿轴套是齿顶面为球面、齿向为鼓型修形的齿轮，内齿轴套是标准的直齿圆柱齿轮。在传统鼓型齿轮副基础上，本文中提出一种新型含过渡齿套的鼓型齿轮副，简称新型结构，如图1（b）所示。新型鼓型齿轮副包括内齿轴套、过渡齿套和外齿轴套。该新型结构的内、外齿轴套并非直接接触，而是通过过渡齿套来传递转矩。过渡齿套的外齿为外花键，与内齿轴套上的内花键联接。过渡齿套的内齿与外齿轴套上的鼓型齿相啮合。

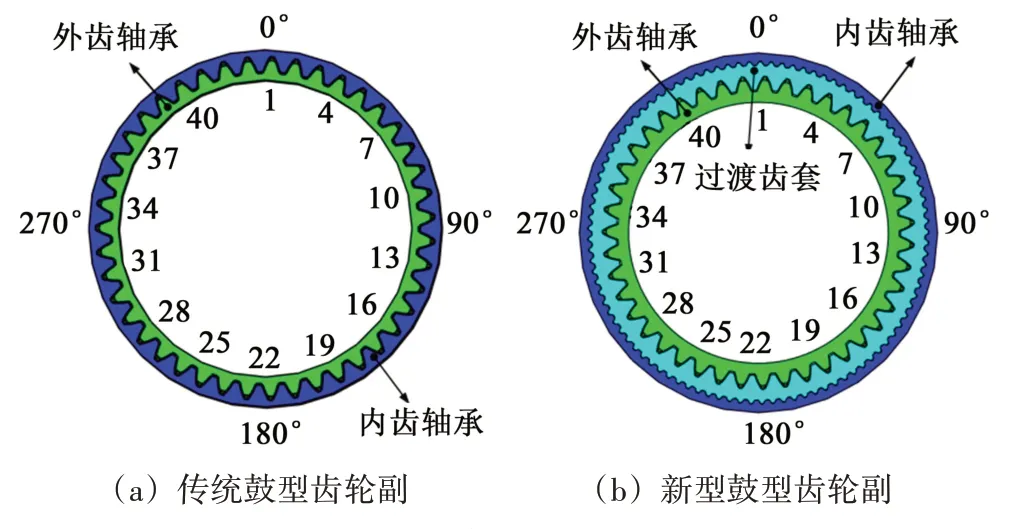
图1 两种鼓型齿轮副结构Fig.1 Two kinds of crown gear pair structures

相较于普通圆柱齿轮副的运动规律，鼓型齿联轴器的运动是复杂的空间运动[12]。鼓型齿轮副在无倾角、有倾角时的齿面啮合状态分别如图2（a）、图2（b）所示。为方便分析，沿顺时针方向，把鼓型齿轮副的运动位置依次规定为转角0°、90°、180°、270°；同时将0°转角位置上的鼓型齿规定为1 号轮齿，沿着顺时针的方向依次标记轮齿，每隔3个轮齿标记一次，直至标记到轮齿40。由于转角相差为180°的轮齿处运动状态是一样的，因此，只分析0°～180°转角区间内轮齿的运动状态即可。无倾角的情况下，由于各个轮齿啮合位置不变，其运动状态也是不变的。在有倾角θ的情况下，其运动状态将经历纯摆动区、摆动和翻转复合区、纯翻转区、翻转和摆动复合区、纯摆动区[13]。

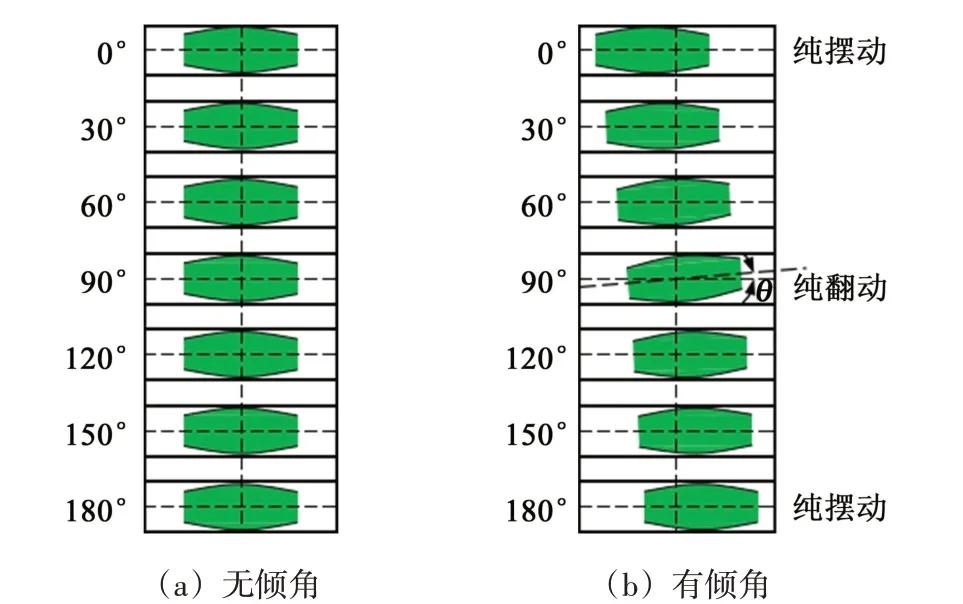
图2 鼓型齿轮副结构运动规律Fig.2 Movement law of the crown gear pair structure

1.2 鼓型齿轮副啮合有限元模型

实践表明，鼓型齿轮副的失效部位主要发生在啮合齿面上。为使计算结果更加可靠并考虑到计算规模对计算机的要求，在保证外齿轴套和内齿轴套受力分析准确性的前提下，可以使外齿轴套与内齿轴套采用相同宽度，且减薄两者的厚度。

分别建立外齿轴套、过渡齿套以及内齿轴套全部轮齿的三维实体模型，然后按照设定的不同轴间倾角进行组合装配。本文中分析的新型鼓型齿轮副的几何设计参数如表1所示。

表1 新型鼓型齿轮副参数Tab.1 Parameters of the new crown gear pair

将装配后的三维实体模型导入Hypermesh 软件中进行网格划分。由于在啮合过程中参与啮合的主要是轮齿，所以应加密轮齿网格，保证接触区域的网格密度满足计算精度的要求，齿轮基体网格可以稍微稀疏一些。共划分了963 840 个单元，1 112 760 个节点。采用同样的划分方法，传统的鼓型齿轮副共划分了584 800 个单元，701 760 个节点。鼓型齿轮副的材料为42CrMo，弹性模量为2.06×1011Pa、泊松比为0.3。

将划分好的有限元网格模型导入到Ansys Workbench 的瞬态动力学模块，进行有限元分析。分析传统鼓型齿轮副时，对外齿轴套和内齿轴套各施加一个旋转副，保证两者仅有1个转动自由度；外齿轴套作为主动轮施加转速500 r/min，内齿轴套作为从动轮施加转矩1 147 kN·m。分析新型鼓型齿轮副时，对外齿轴套和内齿轴套施加与前述相同的边界条件，对过渡轴套施加转动自由度。上述旋转副使用MPC184 单元，接触区使用CONTA174 和TARGE170单元。由于二次单元会导致等效节点接触力在角节点和边中节点之间震荡[14]，所以，齿轮副主体使用Solid185单元。新型鼓型齿联轴器两组接触面之间为有润滑的滑动摩擦，设置其摩擦因数为0.1。

2 结果与讨论

2.1 对中状态下两种鼓型齿轮副的啮合特性

图3所示为无倾角情况下两种齿轮副结构的等效应力。如图3（a）所示，外齿轴套齿面上的等效应力大致呈半椭圆形分布，在齿根部位发生应力集中，最大等效应力为327.07 MPa；如图3（b）所示，内齿轴套齿面上的等效应力大致呈圆形分布，且最大应力发生在外齿轴套与内齿轴套的接触部位，最大等效应力为415.12 MPa。内齿轴套齿面的齿顶部位颜色较深，说明在该位置承受了较大的等效应力。由图3（a）、图3（b）中可知，传统鼓型齿轮副外齿轴套和内齿轴套的各齿面等效应力数值大小大致相等且应力分布一致，较为均匀，符合实际受力状况，内齿轴套的等效应力比外齿轴套大。

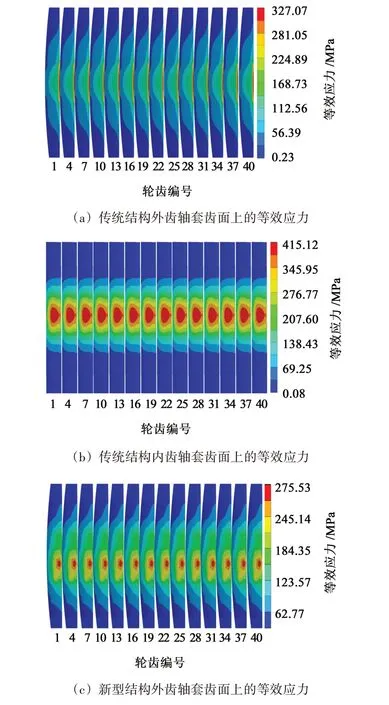
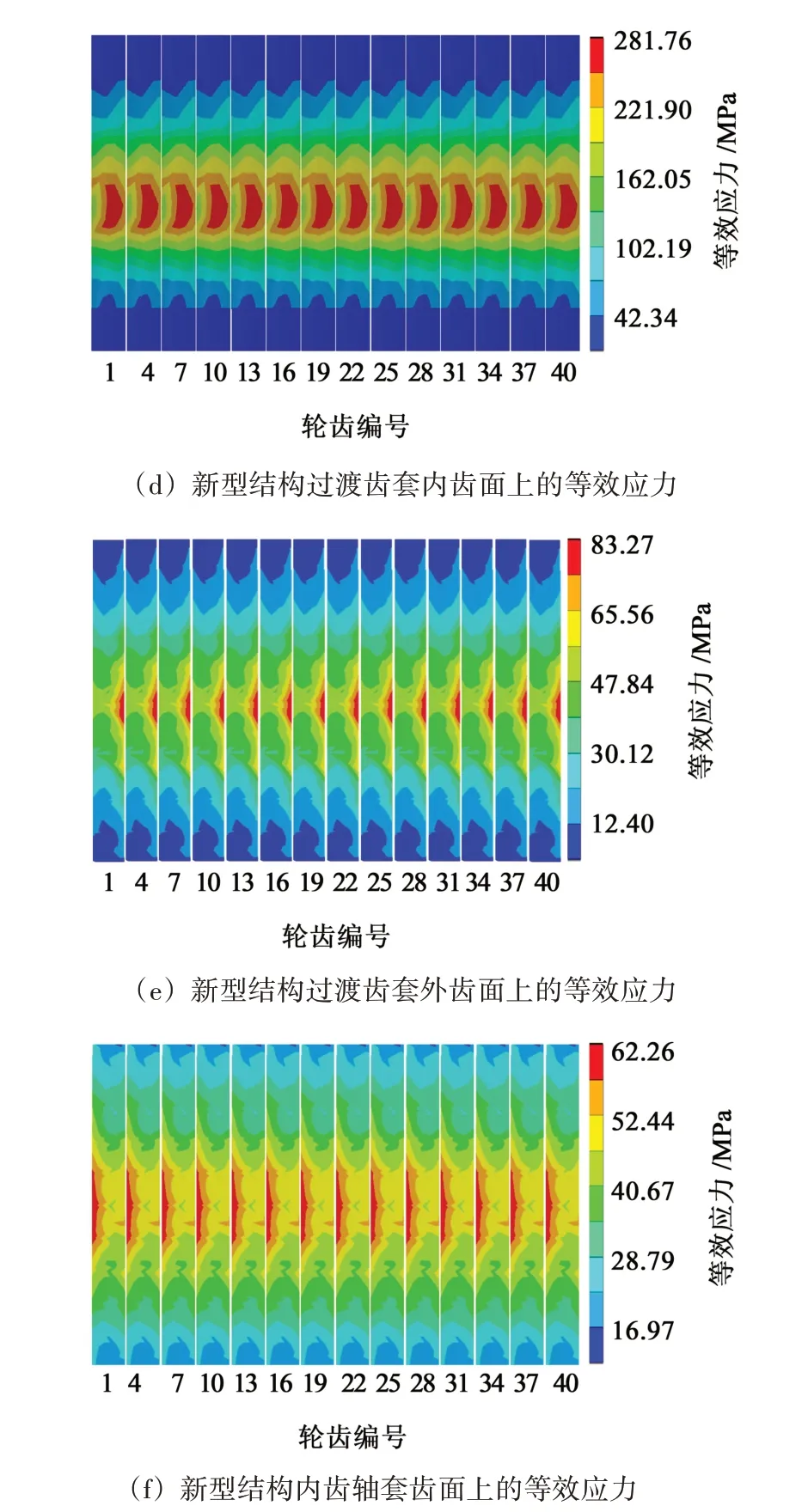
图3 无倾角情况下两种结构的应力对比分析Fig.3 Stress comparison analysis of the two structures without inclination

如图3（c）所示，外齿轴套齿面上的等效应力大致呈圆形分布，最大应力集中在中间鼓肚部位，其峰值为275.53 MPa。与传统结构中的外齿轴套齿面受力分布对比，新型结构外齿轴套的等效应力有所下降，应力集中区域从原来的齿根部位转移到中间鼓肚位置，齿轮副的接触区域发生了改变。如图3（d）所示，过渡齿套内齿面上的最大等效应力为281.76 MPa，最大等效应力出现在外齿轴套与过渡齿套的接触区域。如图3（e）所示，过渡齿套外齿面上的等效应力大致呈半椭圆形分布，在齿根部位发生应力集中，最大应力为83.27 MPa。由于过渡齿套的外齿数较多，故受到的应力比过渡齿套的内齿应力小。如图3（f）所示，内齿轴套齿面上的等效应力大致呈半椭圆形分布，且最大应力发生在与过渡齿套外齿接触的部位，最大等效应力为64.26 MPa。应力分布图中齿根部位的颜色较深，说明该位置同时也受到较大的等效应力。由图3（c）～图3（f）中可知，新型鼓型齿联轴器的外齿轴套、过渡齿套、内齿轴套各齿面上应力数值大小大致相等且应力分布一致，较为均匀，且等效应力只作用在啮合区较小的范围内，过渡齿套内齿上的等效应力比外齿轴套大。

图4 所示为无倾角情况下两种结构的应变对比分析。如图4（a）所示，传统结构中的外齿轴套齿面上的等效应变大致呈半椭圆形分布，最大等效应变为0.001 746。如图4（b）所示，内齿轴套齿面上等效应变大致呈圆形分布，最大等效应变为0.002 14，等效应变只分布在啮合区较小的范围内，且等效应变在除轮齿啮合面外其余部分的分布较少且较小。传统结构中的外齿轴套应变要小于内齿轴套应变，说明内齿轴套受力时的变形要大。如图4（c）所示，新型结构中的外齿轴套应变大致呈圆形分布，应变集中在中间鼓肚部位，最大等效应变为0.001 873。与传统结构中的外齿轴套对比，新型结构中的外齿轴套等效应变有所上升，应变发生区域从原来的齿根部位沿着齿高方向过渡到中间鼓肚位置，接触变形区域发生了改变。如图4（d）所示，过渡齿套内齿面的最大等效应变为0.001 682，出现在外齿轴套与过渡齿套内齿接触区域，与传统结构中内齿轴套相比，应变明显降低，说明新型结构中过渡齿套内齿面的应变得到改善，应变集中区域也有一定改变。

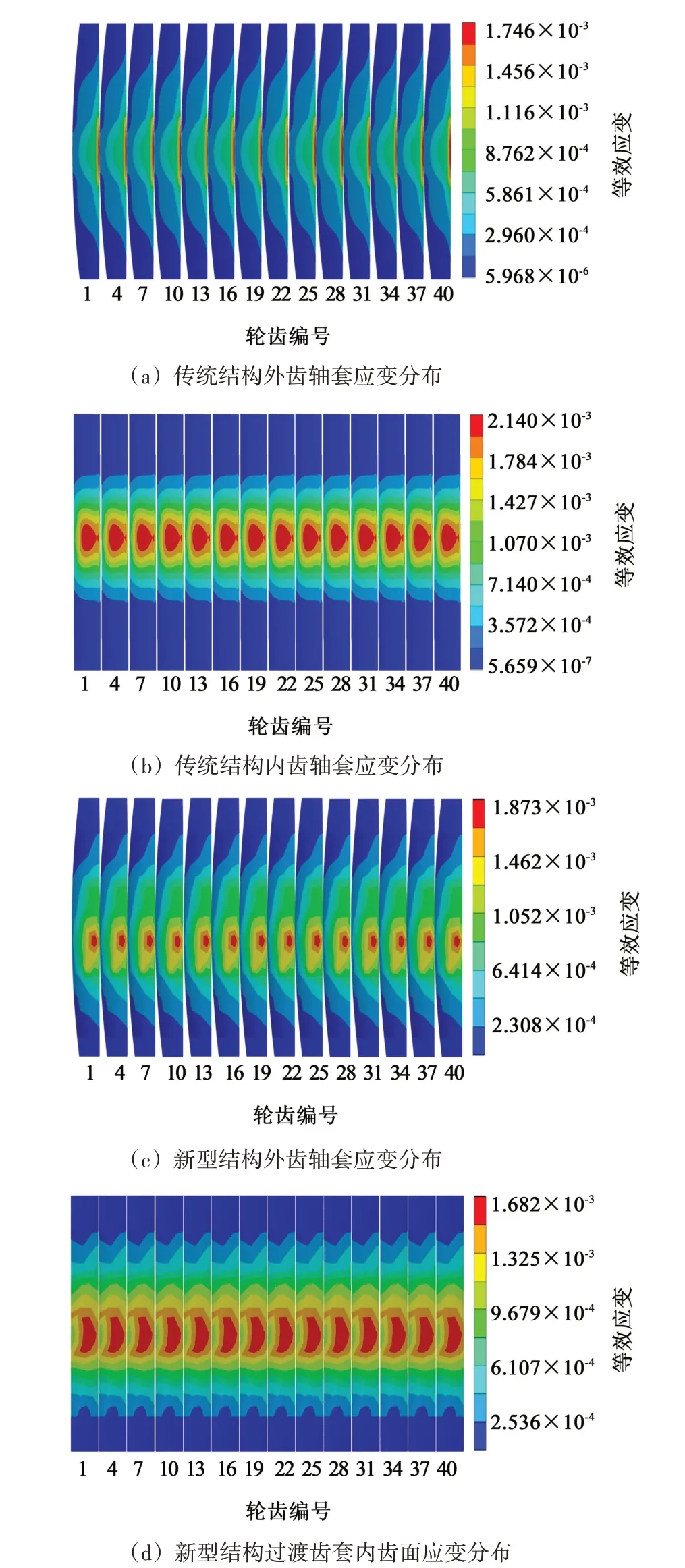
图4 无倾角情况下两种结构的应变对比Fig.4 Strain comparison of the two structures without inclination

图5所示为无倾角情况下两种结构的有限元分析结果。相比传统鼓型齿轮副，新型鼓型齿轮副中的外齿轴套和过渡齿套内齿上的应力均有显著降低。传统鼓型齿轮副系统的最大等效应力和应变发生在与外齿轴套相啮合的内齿轴套上，最大等效应力为415.12 MPa、最大等效应变为0.002 14；新型鼓型齿轮副系统中的最大等效应力和应变发生在与外齿轴套相啮合的过渡齿套上。与传统齿轮副系统相比，新型结构中的最大等效应力降低了32.12%、最大等效应变降低了21.4%。

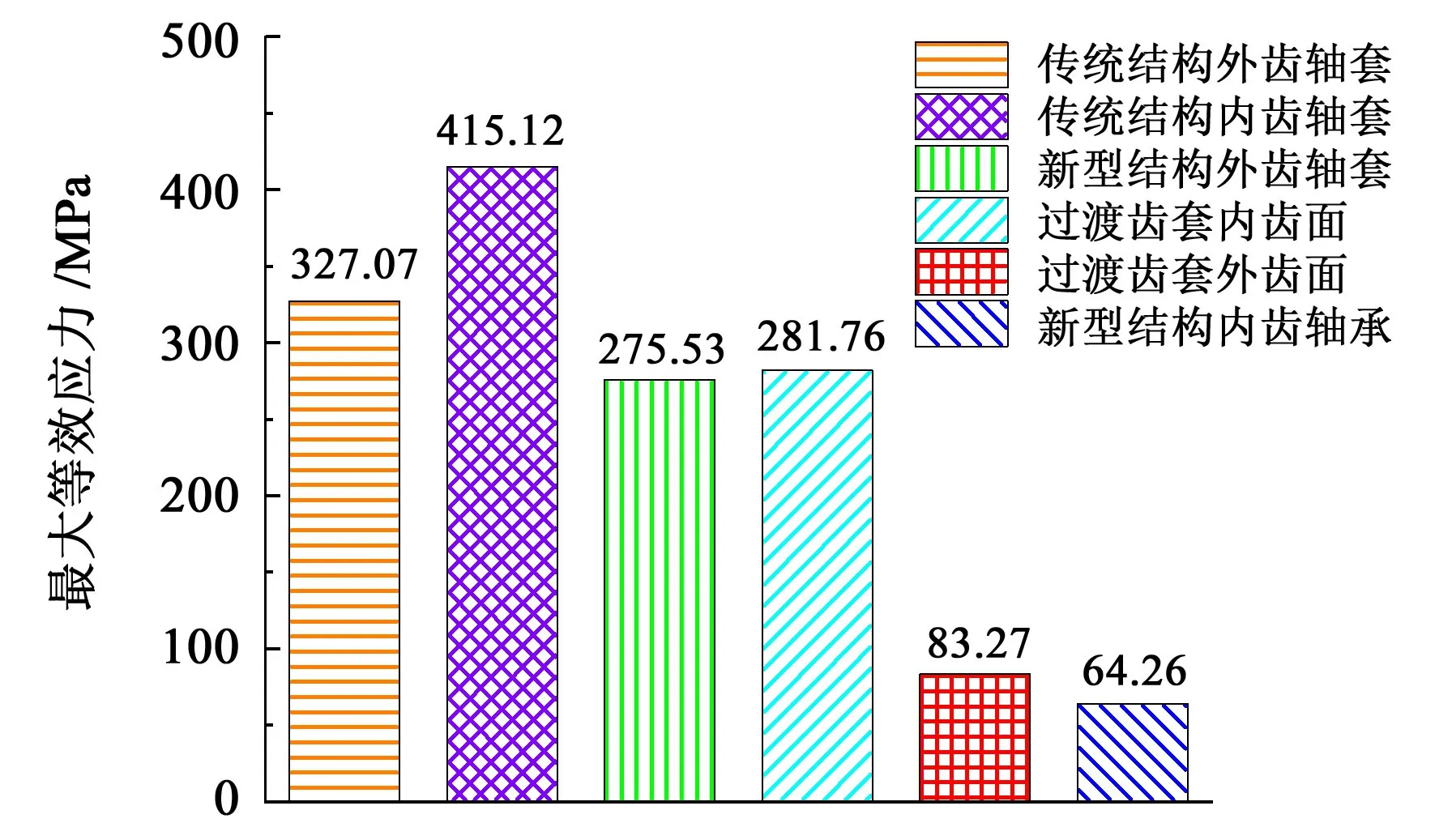
图5 无倾角情况下两种结构有限元分析结果对比Fig.5 Comparison of finite element analysis results of the two structures without inclination

2.2 考虑轴间倾角时鼓型齿轮副啮合性能

图6 所示为在轴间倾角为0.3°下两种齿轮副结构的等效应力。如图6（a）所示，传统鼓型齿轮副中的外齿轴套齿面上的应力集中在齿根处，最大等效应力为372.96 MPa，其中在中间鼓肚处也出现了黄色区域，说明在该处也发生了轻微应力集中；如图6（b）所示，传统鼓型齿轮副中的内齿轴套上最大应力出现在外齿轴套与内齿轴套接触的位置，最大等效应力为457.77 MPa。由于受到轴间倾角影响，传统鼓型齿轮副的啮合状态是不断发生改变的，每个鼓型齿上的应力分布是不相同的，其应力分布由对中情况下的齿宽中部位置向两边端部移动，大致呈周期性分布。

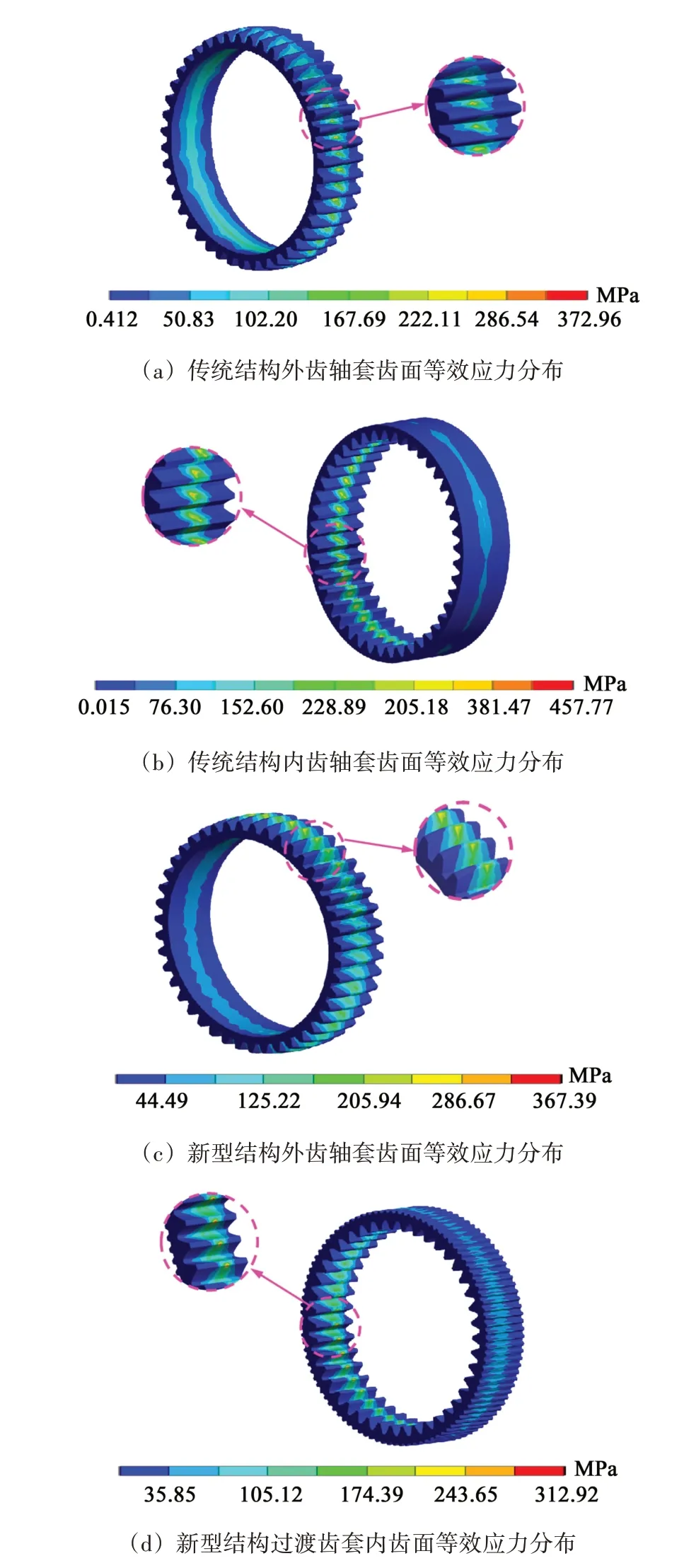
图6 倾角0.3°下两种结构的应力对比分析Fig.6 Stress comparison analysis of the two structures with an inclination angle of 0.3°

新型结构的外齿轴套和过渡齿套的内齿面应力分布分别如图6（c）和图6（d）所示。由图6（c）中可知，外齿轴套应力在齿顶和齿根处都出现较大应力，其峰值为367.39 MPa。从单齿接触区域可以看出，随着轴间倾角的出现，鼓型齿面啮合区域的接触形状是不规则和变化的，每个轮齿上等效应力的分布和数值范围都是不相同的。从全齿来看，接触区域为一与偏移角相关的空间曲线，最大等效应力出现在纯翻转处附近，且纯翻转处应力分布区域最大，距离纯翻转处越远，应力分布区域越小、越少，且在纯翻转处两边对称分布。与传统鼓型齿轮副中的外齿轴套齿面受力分布对比，新型结构外齿轴套的等效应力有所降低，接触区域发生了改变。由图6（d）中可知，过渡齿套内齿面的最大等效应力为312.92 MPa，出现在外齿轴套与过渡齿套内齿接触区域，与传统结构中的内齿轴套受力情况相比，应力明显降低，说明新型结构过渡齿套内齿的应力得到了一定的改善。

图7 所示为倾角在0.3°下两种齿轮副结构的等效应变。如图7（a）所示，在外齿轴套齿面上的等效应变大致呈半椭圆形分布，主要集中在齿根部位，最大等效应变为0.001 968。如图7（b）所示，内齿轴套齿面上的等效应变大致呈圆形分布，最大等效应变为0.002 361，等效应变分布在外齿轴套与内齿轴套接触区域。传统结构中的内齿轴套应变要大于外齿轴套应变，说明内齿轴套受力时的变形要大。如图7（c）所示，新型结构中的外齿轴套应变大致呈椭圆形分布，应变集中在齿顶和齿根部位，最大等效应变为0.002 4。与传统结构中的外齿轴套对比，新型结构中的外齿轴套的等效应变有所上升，接触变形区域发生了改变。如图7（d）所示，过渡齿套内齿面的最大等效应变为0.001 988，出现在外齿轴套与过渡齿套内齿接触区域，与传统结构中的内齿轴套相比，应变明显降低，说明新型结构下过渡齿套内齿面的应变得到改善，应变集中区域也有一定改变。

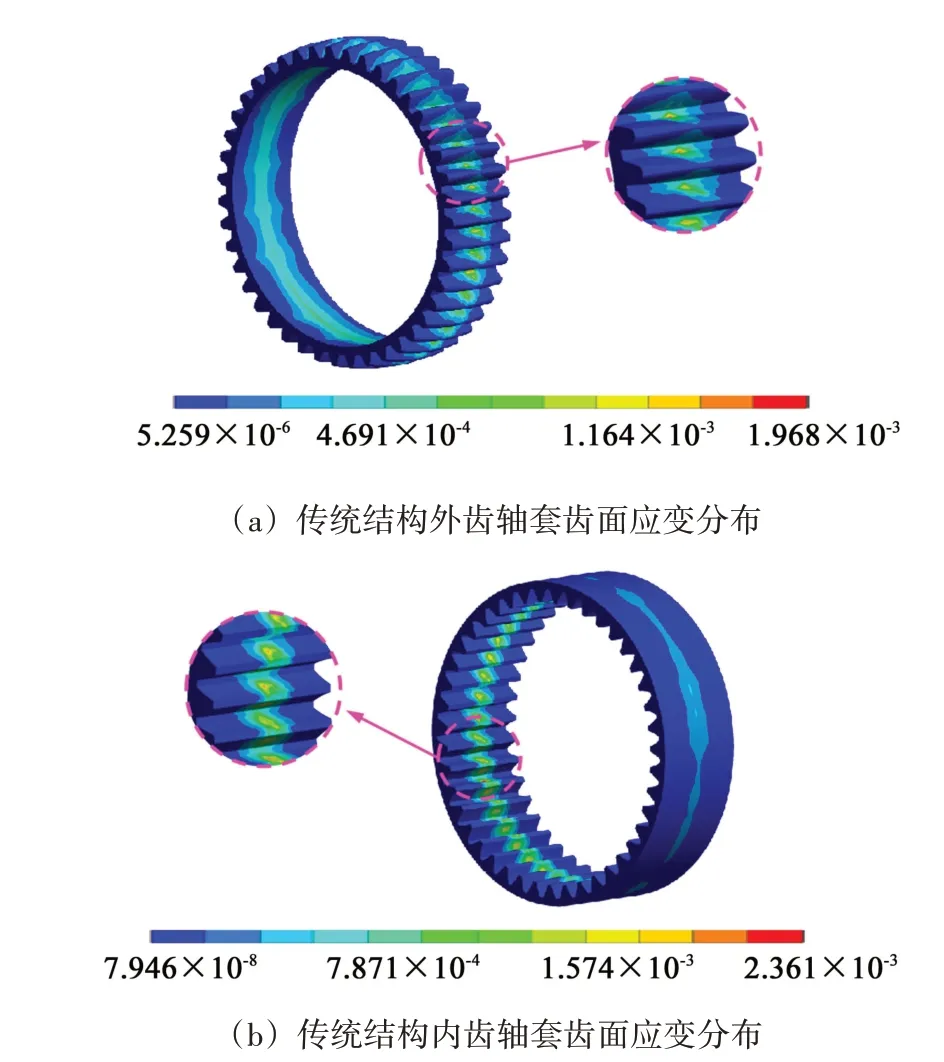
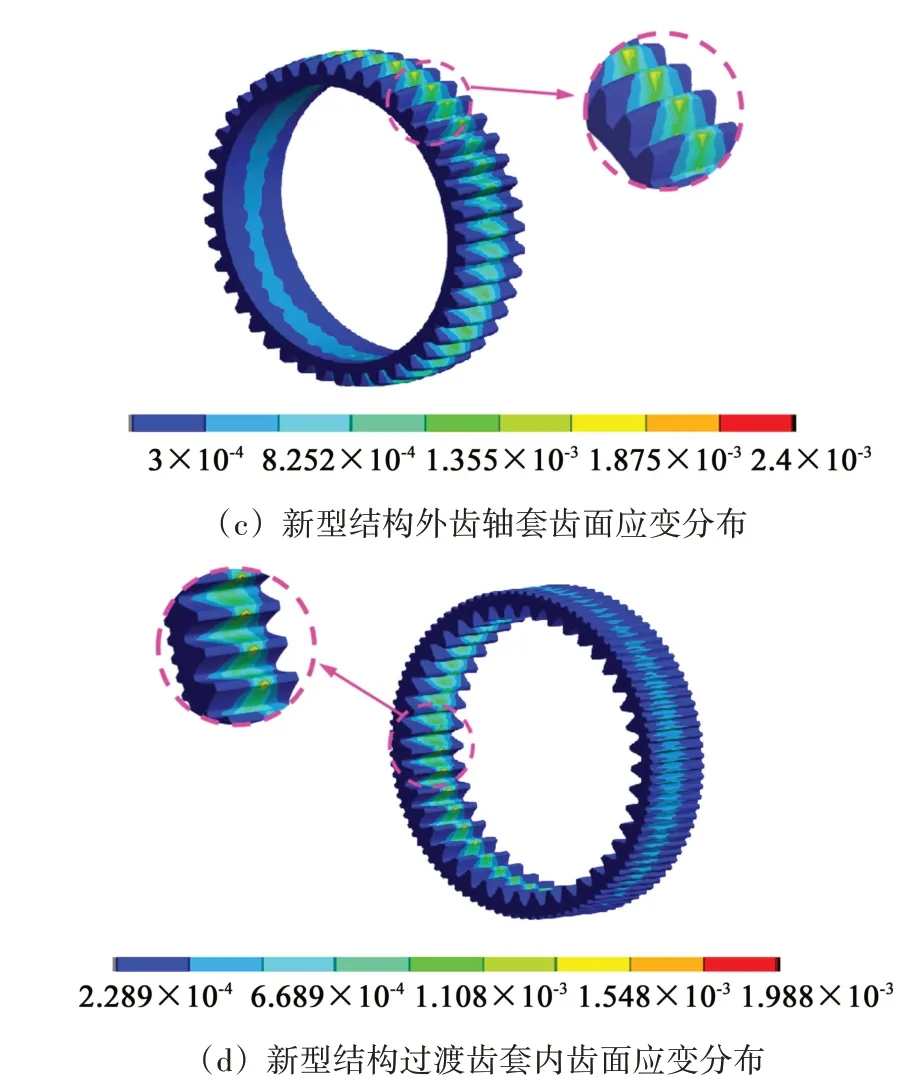
图7 倾角0.3°下两种结构的应变对比分析Fig.7 Strain comparison analysis of the two structures with an inclination angle of 0.3°

图8所示为不同轴间倾角下两种结构最大等效应力的变化。如图8（a）所示，随轴间倾角增大，传统鼓型齿轮副内齿轴套和外齿轴套上的最大等效应力增大，且内齿轴套的应力要大于外齿轴套的应力。如图8（b）所示，随着轴间倾角增大，新型鼓型齿轮副中的外齿轴套应力先增后降，过渡齿套内齿面应力先缓慢增大后较大幅度增大。通过增设过渡齿套，应力会发生转移，外齿轴套的部分应力转移到过渡齿套上。但在轴间倾角为0.3°时，外齿轴套应力要大于过渡齿套内齿面的应力，说明此时应力并未发生转移。总的来看，新型结构降低了鼓型齿轮副的最大等效应力，有助于提高承载能力。但其中过渡齿套承受应力较大，可能最先失效。

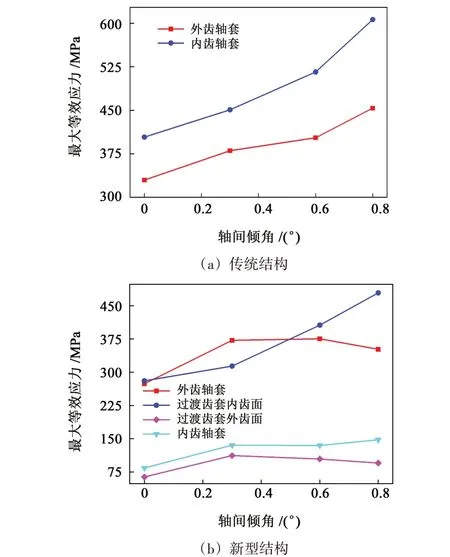
图8 轴间倾角对应力的影响Fig.8 Influence of the inclination angle between the shafts on the stress

图9所示为不同轴间倾角下两种结构最大等效应变的变化。如图9（a）所示，随着轴间倾角的增大，传统鼓型齿轮副中内齿轴套和外齿轴套的最大等效应变都随之增大，最大等效应变出现在纯翻转处附近，距离纯翻转处越远，应变分布区域越小、越少。如图9（b）所示，随轴间倾角增大，新型鼓型齿轮副中的外齿轴套应变先增后降，过渡齿套内齿面应变先缓慢增大后大幅度增大，外齿轴套齿面应变略高于过渡齿套内齿面应变，最大应变出现在鼓型齿面的接触部位。相比传统结构，外齿轴套的应变几乎没有变化，而过渡齿套内齿面的应变显著降低。综上分析可见，随轴间倾角增大，传统鼓型齿轮副中的最大等效应力和应变增大；随轴间倾角增大，新型鼓型齿轮副结构中的外齿轴套等效应力和应变将部分转移到过渡齿套上。因此，新型结构中的外齿轴套在较大倾角下仍能保持较低等效应力，对成本高昂的外齿轴套起到有效保护作用。

图9 轴间倾角对应变的影响Fig.9 Influence of the inclination angle between the shafts on the strain

2.3 新型鼓型齿联轴器制造与运行

面向某轧钢厂设计、制造了含过渡齿套的鼓型齿联轴器，并装机运行。如图10（a）、图10（b）所示，经分动箱将电机动力和运动分别传递至上下布置的两个鼓型齿联轴器，联轴器传动轴带动鼓型齿轮副运转，轧机侧齿轮副的内齿轴套分别与上、下轧辊固联，从而实现轧机的轧制作业。轧机组上的新型鼓型齿联轴器运行半年，总体状态良好。

图10 新型鼓型齿联轴器的装机运行图Fig.10 Installation and operation diagrams of the new crown gear coupling

定期检修拆解时发现，鼓型齿轮副齿面工作状态良好，无明显点蚀、磨损、胶合等齿面失效现象。图11所示为拆解后的新型鼓型齿轮副，图11（a）中的外齿轴套与图11（b）中的过渡齿套内齿啮合，图11（b）中的过渡齿套外齿与图11（c）中的内齿轴套内齿啮合。鼓型齿轮副各组件齿面上的接触状况有所不同，过渡齿套内齿和外齿齿面上出现轻微磨痕，而外齿轴套和内齿轴套齿面状态相对较好。前述有限元分析结果同样表明，与传统鼓型齿轮副系统承受应力相比，在新型鼓型齿轮副系统中，外齿轴套的等效应力降低，过渡齿套内齿等效应力高于外齿轴套应力，过渡齿套承受着较高应力。因此，现场实际运行状况与有限元分析结果相符。新型鼓型齿联轴器中，过渡齿套对外齿轴套和内齿轴套起到一定保护作用。