凸轮转子外摆线轮廓的3种特定形态及其性能分析
2022-10-21陈庆红李玉龙张平山
陈庆红 李玉龙 张平山
(1 福建林业职业技术学院 信息工程系, 福建 南平 353000)
(2 宿迁学院 机电工程学院, 江苏 宿迁 223800)
(3 华闽南配集团股份有限公司, 福建 南平 353000)
0 引言
凸轮转子泵是一种应用广泛的容积式流体设备,一对同尺寸的转子为泵的核心部件,并通过其轮廓将转子室分隔成若干个小空间;随着转子副的连续旋转,驱使这些小空间发生周期性变化,从而实现物料吸排的泵送目的[1]。其中,转子轮廓的构造质量直接决定了物料的泵送品质[2]等诸多性能[3-4],且与泵送流量间构成了明确的因果关系[5]。转子轮廓的优化目的在于提高转子泵的综合性能[6],主要体现为尽可能小的单位排量体积、流量脉动系数和尽可能少的泵内泄漏等。目前,在顶圆弧过渡的叶型构造中,渐开线[7]、圆弧[8]和圆摆线[9]的应用最普遍。其中,圆摆线一般采用180°滚动周期下的外摆线[10],而非180°滚动周期下的外摆线构造则相对较少[11]。有鉴于此,本文中拟以滚径比为变量,以泵的最佳综合性能为目标,探究非180°滚动周期下的外摆线轮廓构造。
1 外摆线转子的轮廓构造
图1 中,外摆线转子的半叶轮廓由顶圆弧01、外摆线12、内轭线23 和根圆弧34,共4 段首尾相连组成。其中,顶圆弧01 和根圆弧34 为过渡轮廓段,不参与转子副的共轭运动,外摆线12 和内轭线23 为工作轮廓段,承担转子副的共轭运动;O、O′分别为本体转子、配对转子的中心,O0、O4 为顶、根(对称)轴,顶、根轴间的角平分轴为中轴O2,顶轴与中轴、中轴与根轴的夹角均为共轭圆心角φ,φ=0.5π/N,N为转子叶数,即转子副的重合度为1;顶、根圆弧的圆心分别为顶轴、根轴与节圆的交点5、交点6;外摆线成形的定圆、滚圆半径分别为节圆半径R、r,滚径比i=r/R,滚圆圆心为o;转子副间的间隙为δ。
依据转子副间隙为[12]
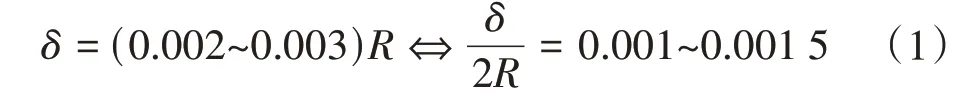
选用原则,可以忽略δ对转子轮廓的构造影响。
图1 所示给出了转角为θ时转子副轮廓间的共轭关系。其中,转角以中轴O2 为旋转的起始位置,0≤θ≤φ。

图1 外摆线转子的轮廓构造Fig.1 Profile construction of epicycloid rotors
在图1 所示的XOY直角坐标系下,设本体转子外摆线上对应的共轭点为点7(x7,y7),点7 处法线与节圆的交点为转子瞬心点8(x8,y8),78 连线的长度为转动瞬径ρ,78 连线与O8 连线间夹角为传动角α,α≤90°,滚圆以点2 为起点的滚动角∠7o8 为β,点8 关于中轴O2 对称的点为8′(x8′,y8′),点8′在内轭线23 上的垂足为共轭点7′(x7′,y7′)。即,在同一转子的轮廓上,点7 与点7′存在着先中轴O2、后瞬心处节圆切线8′8"的双对称几何关系。
外摆线成形原理为
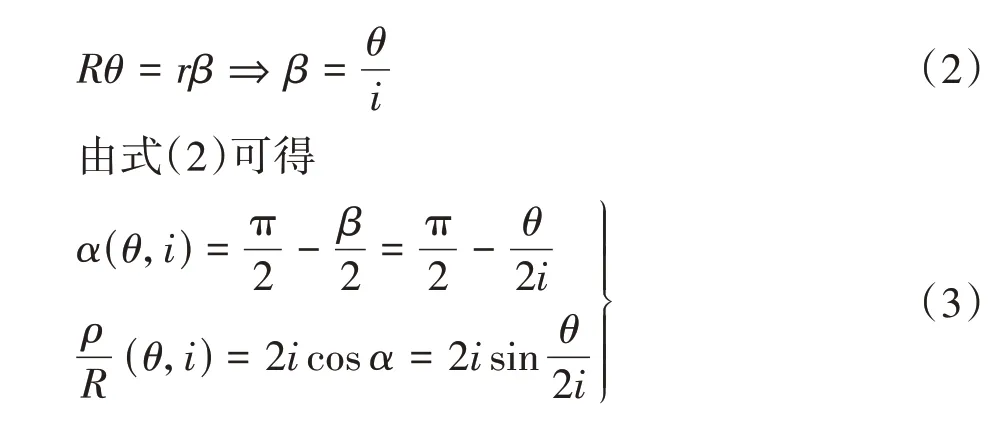
由式(3),点8(x8,y8)和点7(x7,y7)表达式分别为

由式(4)可得,外摆线12的成形方程(x12,y12)为
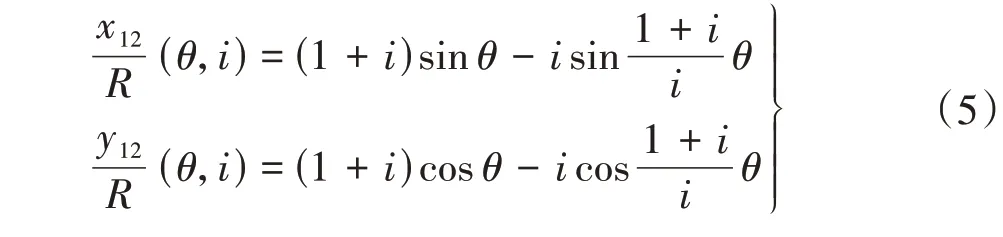
由式(3)、点8′(x8′,y8′)和点7′(x7′,y7′)的表达式为
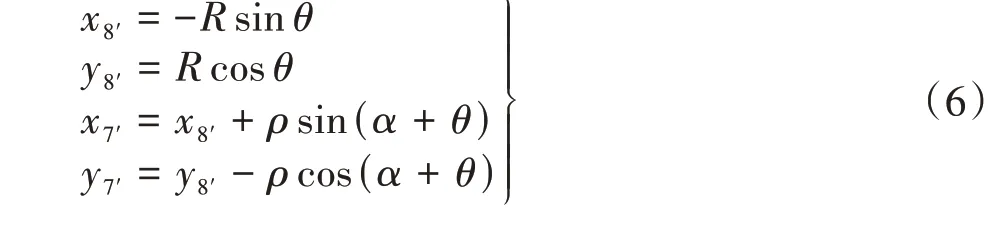
由式(6)可得,内轭线23的成形方程(x23,y23)为
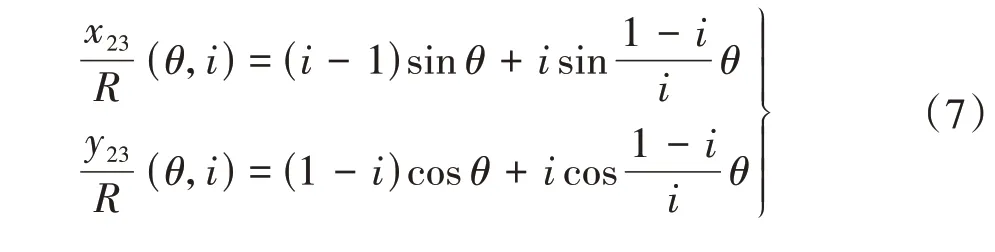
2 外摆线转子的3种特定形态
设α0、ρ0分别为外摆线轮廓端点1 处的传动角α和转动半径ρ,ε为转子的形状系数,其中,α0也为顶圆弧01和根圆弧34的圆心角。
由式(3)及θ=φ=0.5π/N可得
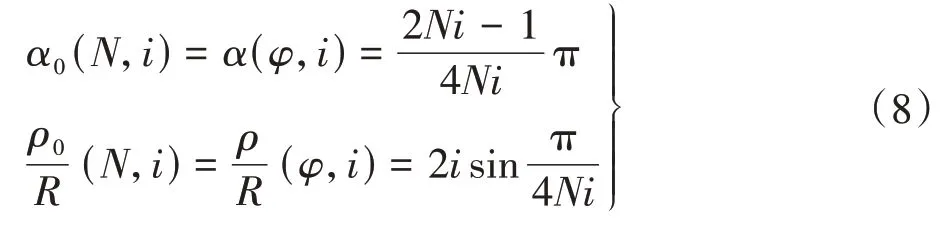
由式(8)可得转子的形状系数ε为
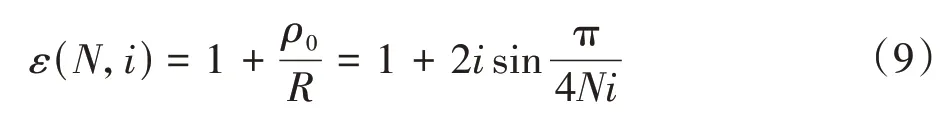
由式(7)中横坐标x23表达式为
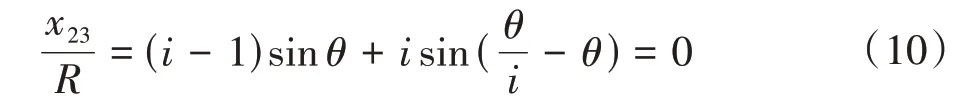
由式(10)可得i=0.5、1.0。其中,对应的纵坐标y23为
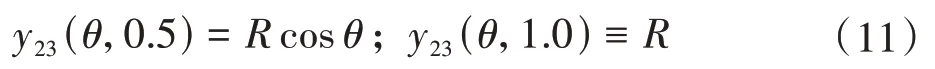
以N=3 为例,外摆线随i=1/6、0.5、1、1.5 的形态变化,如图2所示。其中
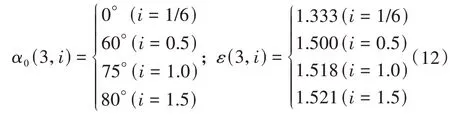
由图2 和式(12)知,i越大,ε越大。其中,i=1/6 时,α0=0°、β=0°~180°滚动周期下的轮廓构造,如图2(a)所示。此时,并无顶圆弧和根圆弧,且内轭线为节圆内的圆内摆线,此为常见180°滚动周期下的等幅圆摆线轮廓构造。
i=0.5 时,α0=60°、β=0°~60°滚动周期下的轮廓构造,如图2(b)所示。此时,内轭线为与中轴重合的直线段,这与由式(9)~式(10)给出的(x23,y23)=(0,Rcosθ)完全一致。
i=1.0 时,α0=75°、β=0°~30°滚动周期下的轮廓构造,如图2(c)所示。此时,内轭线收缩为轮廓点2,这与由式(9)~式(10)给出的(x23,y23)=(0,R)完全一致。
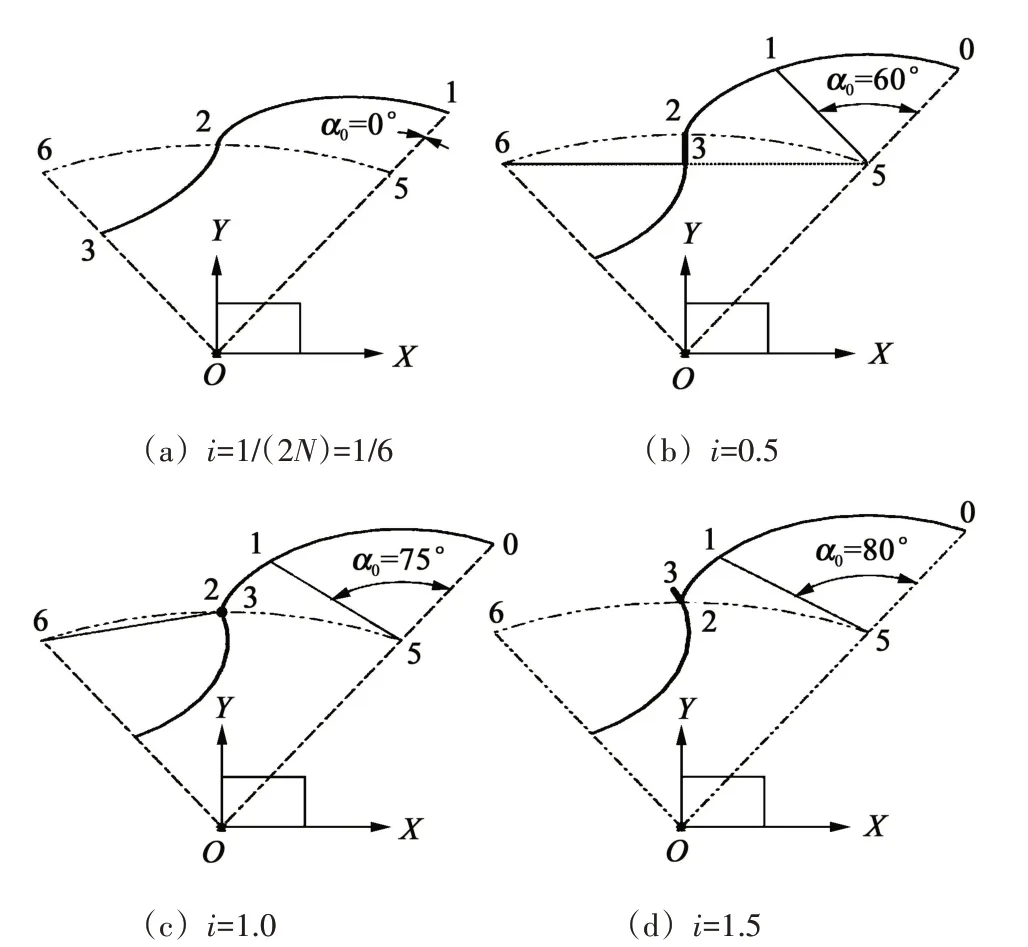
图2 理论轮廓的3种特定形态Fig.2 Three specific forms of theoretical profile
i=1.5>1时,内轭线23存在几何干涉,不符合作为转子轮廓的要求,如图2(d)所示。
由此可知,在顶圆弧过渡的任意叶型构造中,i=1 的外摆线能取得任意叶型下的最大形状系数;其次,i的取值范围为0.5/N≤i≤1。即i=0.5/N、0.5、1.0 为外摆线转子轮廓的3 种特定形态,对应的内轭线分别具有内摆线、直线段、固定点型的轮廓特征。
3 形状系数和容积利用系数
由式(9)可得,3 种特定形态下转子的形状系数分别为
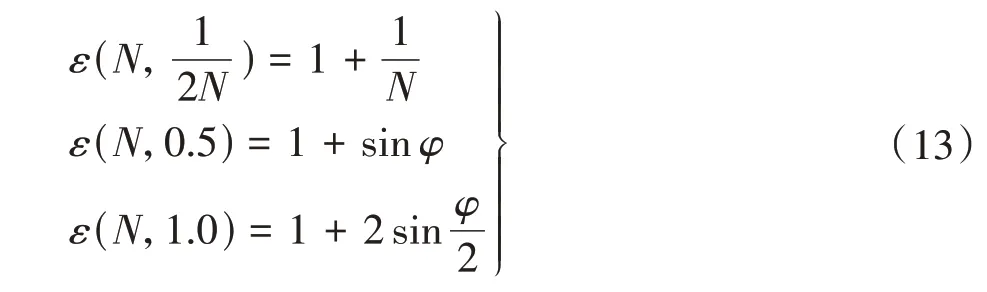
由文献[13],有
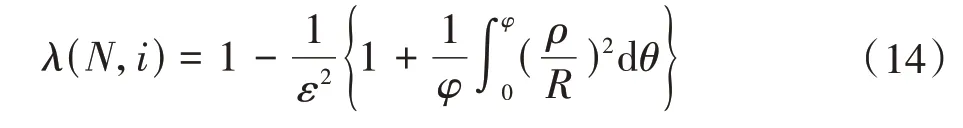
外摆线转子的容积利用系数λ为
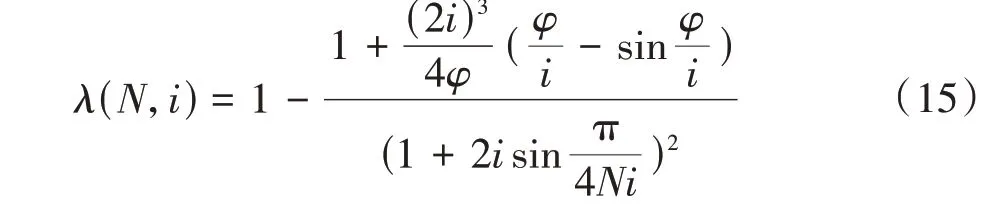
其3种特定形态下对应的容积利用系数λ分别为
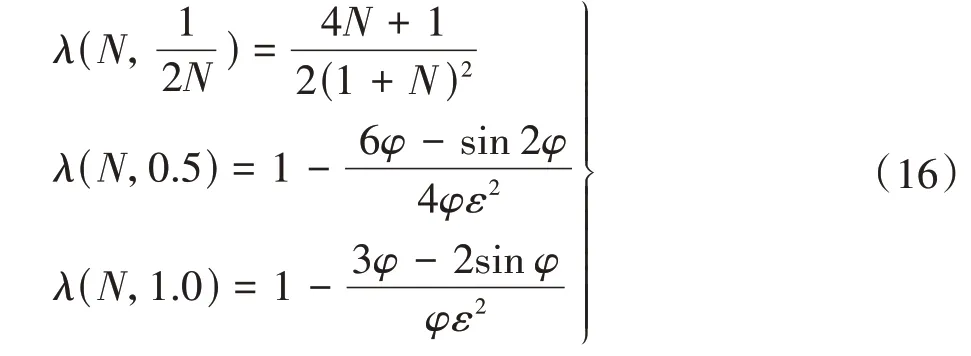
以N=3 为例,ε、λ随i的变化,如表1 所示。其中,0.5/N=1/6≤i<0.5时,i对ε、λ的影响较大,ε增大了12.5%,λ增大了27.3%,转子间因属于凸-凹缝隙流,共轭间隙δ处的泄漏(简称为共轭泄漏)相对较小;0.5<i≤1 时,i对ε、λ的影响很小,ε仅增大1.2%,λ仅增大1.9%,且因属于凸-凸缝隙流,共轭泄漏相对较大;i=0.5 时,因属于凸-平缝隙流,共轭泄漏居中[14]。即,i越大,ε、λ越大,但变化在i=0.5附近快速趋缓,即具有前急后缓的影响特点。

表1 形状系数和容积利用系数随滚径比的变化Tab.1 Changes of shape factor and volume utilization factor with rolling radius rate
所以,i=0.5 外摆线为兼顾ε和λ数值最大化、共轭泄漏最小化、V 型易加工的一个较理想的转子轮廓,如图3(a)所示。3 叶时,1.5 的形状系数比圆弧转子的1.477 0 大1.6%、渐开线转子的1.463 8[15]大2.5%;0.517 的容积利用系数比圆弧转子的0.503 5大2.7%、渐开线转子的0.499 8大3.4%。
i=1.0时,因点共轭造成缝隙流变成了孔口流[16],共轭泄漏相对最大,但其却具有最大的形状系数和更易加工的节圆内全过渡轮廓,通过节圆半径R的微调,极利于空间相对狭窄的节圆内轮廓采用标准圆孔加工,如图3(b)所示。故,轮廓最简单,加工最容易。
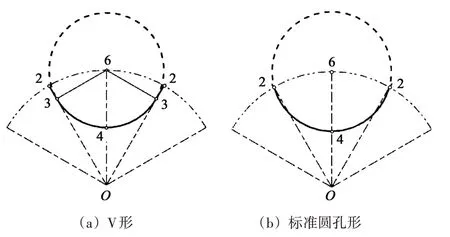
图3 节圆内易加工轮廓Fig.3 Easily machined profile inner the pitch circle
4 理论流量的脉动系数
由文献[17],得外摆线转子泵的理论流量Q为
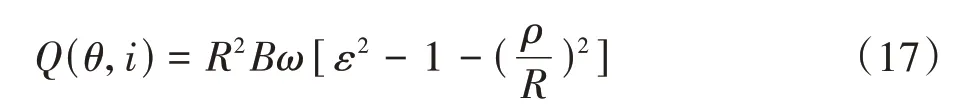
式中,B为转子宽度;ω为转子旋转角速度。
则,理论流量Q的最大流量Qmax、最小流量Qmin、平均流量Qave分别为
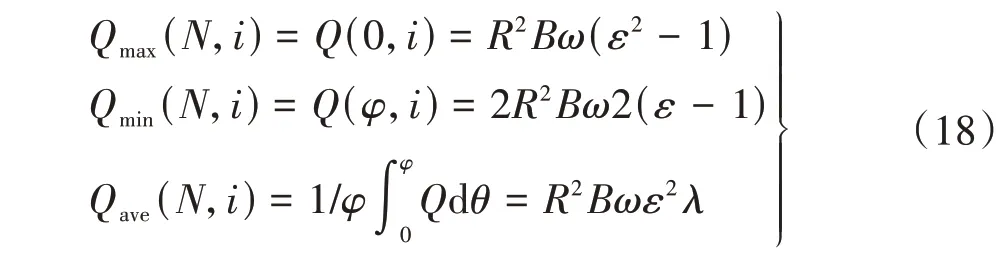
由此,得理论流量Q的脉动系数δ为
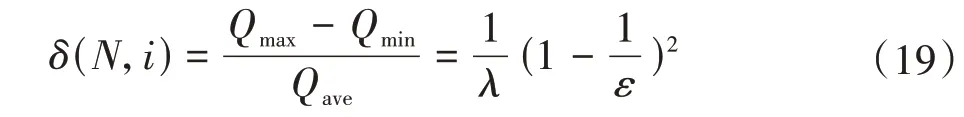
N=3 时,δ随i的变化,如表2 所示。其中,i越大,δ越大,脉动性能越差,但在i=0.5 附近快速变缓。

表2 流量脉动系数随滚径比的变化Tab.2 Changes of flow ripple factor with rolling radius rate
5 理论排量及泵的轻量化
对于转子泵这样的容积泵,转子腔的可利用空间是用于输送工作介质的,在不考虑泄漏、压缩等无容积损失的理论状态下,转子副每转输送的介质量等于可利用空间的容积,而每转输送的介质量等于平均流量Qave乘以每转的时间2π/ω。
由式(18)中的平均流量Qave,得理论排量q为
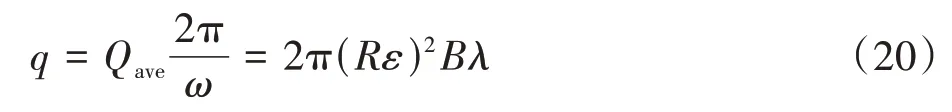
由于转子副所占空间的最小包裹体积即转子腔内体积V0,直接决定了转子泵的整体尺寸与质量,所以,可用KVV0代表泵的总体积V。其中,KV为大于1的体积因子。
此时,由式(20)和
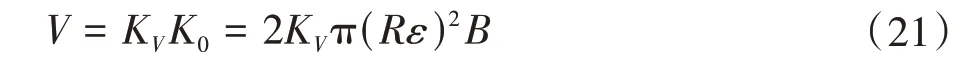
可得单位排量体积qV为
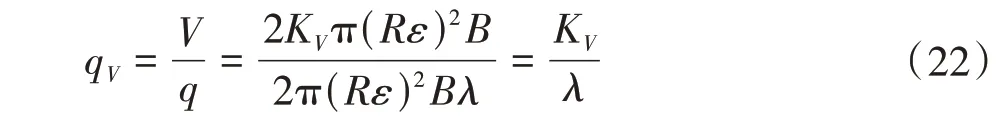
由此可知,i越大,单位排量体积qV越小,轻量化效果越好,但在i=0.5附近快速变缓。
6 结论
(1)同一转子上的外摆线与其内轭线,存在先中轴、后瞬心处节圆切线的双对称几何关系。
(2)由轮廓构造所决定的形状系数和容积利用系数,直接决定了泵的性能,彼此间存在明确的因果关系。
(3)在外摆线轮廓的3种特定形态下,内轭线分别具有内摆线、直线段、固定点型的轮廓特征。
(4)滚径比越大,形状系数越大,轻量化效果越好,但流量脉动性能越差,具有前急后缓的影响特点。
(5)0.5滚径比对应的直型内轭线轮廓,具有综合性能最佳及V型易加工的轮廓特征。
(6)1.0滚径比对应的点型内轭线轮廓,形状系数最大,构造最简单,加工最容易。
