计入热效应的曲轴主轴承润滑性能影响因素分析

2022-10-21王广东毕凤荣

机械传动 2022年10期

邵康王广东毕凤荣

（1 天津大学内燃机燃烧学国家重点实验室，天津 300072）

（2 陆军军事交通学院军事交通运输研究所，天津 300161）

0 引言

曲轴主轴承作为连接曲轴和机体的最关键转动副，是典型的动载荷滑动轴承，起着支撑曲轴和传递载荷的作用。由于内燃机工作环境非常恶劣，工作过程中会产生较大的气缸压力，该压力经活塞、连杆和曲轴传递给主轴承，导致主轴承受到周期性的交变载荷作用，进而会影响内燃机的功率输出、工作寿命和可靠性。

曲轴主轴承在工作过程中，油膜受到剪切力而产生摩擦功耗，会使润滑油温度上升，温度的改变又反过来影响润滑油的黏度，从而改变轴承的润滑性能。因此，主轴承热效应的影响不容忽视。近年来，国内外学者针对内燃机轴承的热效应进行了相应的研究。周玮等[1]以某高功率内燃机主轴承为例，通过使用有限差分法和有限元法联立求解轴承热弹性流体润滑，分析轴承孔位置、形状、轴瓦表面粗糙度和润滑油油品对轴承润滑的影响，发现最大剪切率是评价轴承润滑性能的重要指标，且转速变大，轴承温度上升。Li B 等[2]通过求解广义雷诺方程、热传导方程和能量方程，对不对中轴颈轴承的性能进行了综合分析，发现在转速较低、倾角较大、偏心率较大的情况下，轴颈轴向运动对轴承润滑特性的影响更为明显，轴向运动对轴承润滑性能的影响很大程度上受到热效应和表面粗糙度的影响。Ozasa T等[3]采用流体动力润滑对滑动轴承的运行和设计参数进行了摩擦量纲分析，分析内燃机的动载荷功率损失，提出了一种针对摩擦的简化计算方法，对发动机动载荷下滑动轴承的功率损耗进行了数值计算，并与回归方程估计的功率损耗进行了比较。Bi F R等[4]考虑发动机主轴承的热效应，采用雷诺边界条件对油膜压力进行数值求解，分析过程中考虑了润滑油的黏温特性、表面粗糙度和轴颈倾斜，分析发现，考虑热效应时主轴承的最大油膜压力和最小油膜厚度都会受到影响。Lorenz N 等[5]分别采用二维和三维能量方程建立内燃机轴承热弹性接触模型，分析了油膜温度对润滑油黏度以及承载能力的影响，发现润滑油的温度和剪切率会影响润滑油的黏度。林建辉等[6]采用质量守恒边界条件建立主轴承热弹性流体动力润滑模型，发现考虑温度条件时轴承摩擦功耗偏大，说明温度对油膜有很大影响。杨靖等[7]针对轴承载荷不均导致轴瓦与润滑油非稳态传热现象建立弹性流体动力润滑模型，发现考虑温度场和热变形条件下轴承润滑性能改变明显，轴承磨损严重。滕宪斌等[8]采用有限元法与多体动力学结合的方法建立主轴承润滑模型，分析中考虑主轴承轴颈和轴瓦表面粗糙度、曲轴和轴承座的变形及热效应等影响因素，分析了曲轴轴承间隙、供油压力和温度、油槽宽度等参数变化时的主轴承润滑特性。从上述文献和滑动轴承相关文献中[9-13]可以发现，热效应是影响曲轴主轴承润滑性能的重要因素，对主轴承热效应的分析有助于更好地分析曲轴主轴承的工作状态。但是，上述分析多是从轴承结构参数角度分析轴承温度对轴承润滑性能的影响，忽略了不同轴承载荷与轴承温度的关系。而在分析过程中引入轴承载荷、轴承间隙和轴承温度等影响因素，将有助于对轴承润滑性能的深入分析。

本文中建立了某内燃机曲轴主轴承润滑模型，分析计入热效应的曲轴主轴承润滑性能的影响因素，得到不同影响因素下的主轴承的工作状态。考虑的影响因素主要包括轴承载荷、轴承间隙和进油温度。主轴承的润滑性能通过最大油膜压力、最小油膜厚度、最高轴承温度和最大摩擦功率损失的变化来体现，为内燃机主轴承的设计提供了参考数据。

1 基本理论模型

1.1 润滑油膜方程

曲轴主轴承是典型的动载荷滑动轴承，主轴承载荷随着曲轴转角的变化而不断发生改变。由于内燃机的工作过程是往复周期性运动，因此，曲轴主轴承会受到循环的周期性载荷作用，分析主轴承载荷时，仅分析轴承在稳定工作状态下的1个周期运动即可。润滑油作为曲轴和轴承之间的连接介质，其润滑状态满足弹性流体动力润滑理论，可以通过Reynolds方程进行求解。Reynolds方程为

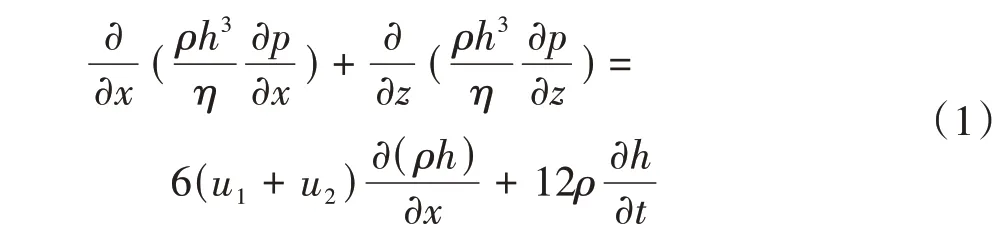
式中，p为油膜压力；h为油膜厚度；ρ为润滑油密度；η为润滑油黏度；u1、u2分别为轴颈和轴承表面速度；x、z均为轴承表面坐标；t为时间。

忽略弹性变形时，轴颈和轴承的油膜厚度h0为

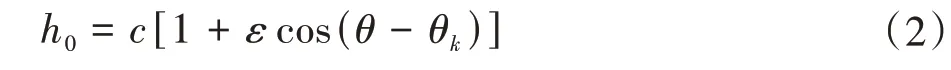
式中，c为轴承间隙；θ为轴承展开角；θk为轴心偏位角；ε为偏心率。

1.2 轴承表面弹性变形

轴承表面在润滑油膜压力的作用下会发生弹性变形。因此，计算时需要考虑结构弹性变形，即主轴承轴颈和轴承的弹性变形。弹性变形的存在会改变轴承油膜厚度。考虑主轴承弹性变形时的油膜厚度为

式中，h0为轴承间隙；R为轴承半径；v（x）为油膜压力作用下的弹性变形。

1.3 轴承载荷方程

为保证主轴承正常工作，曲轴主轴承的载荷在曲轴的每一个转角位置都是平衡的，即轴承受到的外部载荷和主轴承提供的载荷相等，其平衡载荷方程表达式为

式中，x、y分别为轴承水平和垂直方向的坐标；Px、Py均为轴颈外部载荷；Fx、Fy均为轴承油膜支撑载荷；v为轴颈和轴承的相对速度；mj为主轴颈质量。

1.4 能量守恒方程

主轴承的润滑油膜在工作过程中满足瞬态能量方程。分析过程中忽略轴承沿着轴向和切向的热传导，即

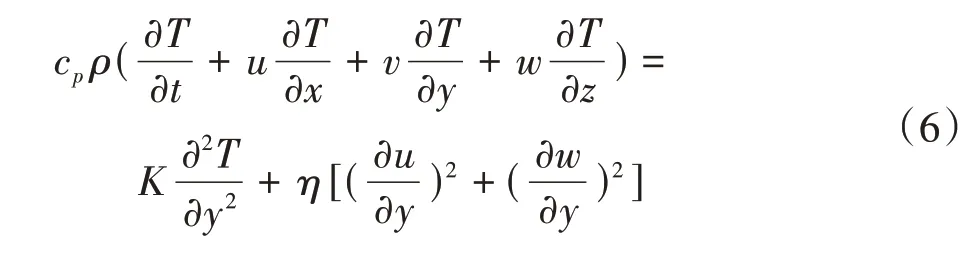
式中，T为轴承温度；K为热传导系数。

1.5 润滑油黏温特性方程

考虑热效应存在时，润滑油的温度会随着轴承工作状态的改变而时刻发生改变，润滑油的黏度也会随之发生变化。计算中，润滑油黏度的整个变化过程采用雷诺黏温方程，其表达式为

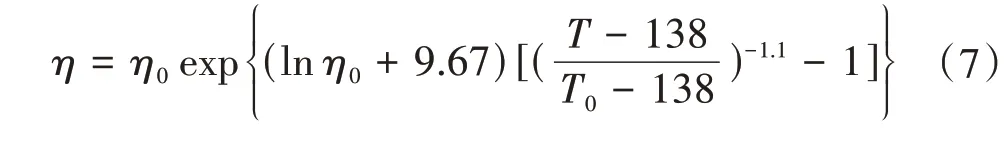
式中，T0为初始温度；T为工作温度；η0为压力为0和温度为T0时的初始黏度。

1.6 摩擦功率损失

主轴承总摩擦因数fall包括了由粗糙度接触引起的摩擦因数fμ和由流体黏度引起的摩擦因数fη，其表达式分别为

对于功率损失Ppowerloss，它等于总摩擦因数fall和主轴颈转速的乘积，即

式中，U为主轴颈转速。

2 计算工况

本文中以内燃机曲轴主轴承为研究对象，建立计入热效应的曲轴主轴承弹性流体动力润滑模型。计算中考虑了润滑油温度随载荷和工况的变化情况，同时，分析了由润滑油黏温效应引起的轴承温度变化，从而分析了温度变化对主轴承润滑性能的影响。主轴承主要计算参数如表1所示。

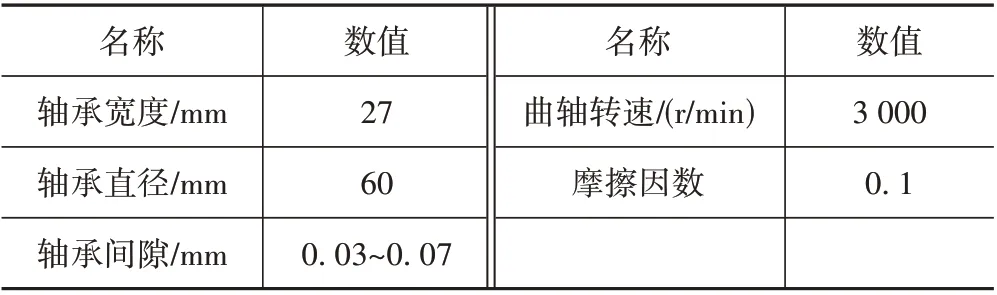
表1 内燃机主轴承主要参数Tab.1 Main parameters of engine main bearing

仿真分析模型中，设定曲轴转速为3 000 r/min，主轴承间隙分别设定为0.03 mm、0.05 mm和0.07 mm，共计3 种工况；主轴承进油温度分别设定为0～120 ℃，中间间隔20 ℃；轴承载荷来自缸内爆发压力，即气缸内压力通过活塞-连杆-曲轴传递给主轴承，该载荷最终由主轴承润滑油膜产生的载荷来平衡。分析模型设定3 种依次变化的轴承载荷，1 个工作周期内轴承外部载荷在水平方向（Px）和垂直方向（Py）的变化曲线如图1 所示，图1 中对应的3 种工况在垂直方向的峰值载荷分别为14 546 N、23 017 N 和31 489 N。

图1 主轴承载荷变化曲线Fig.1 Load variation curve of the main bearing

仿真分析计算流程图如图2所示。

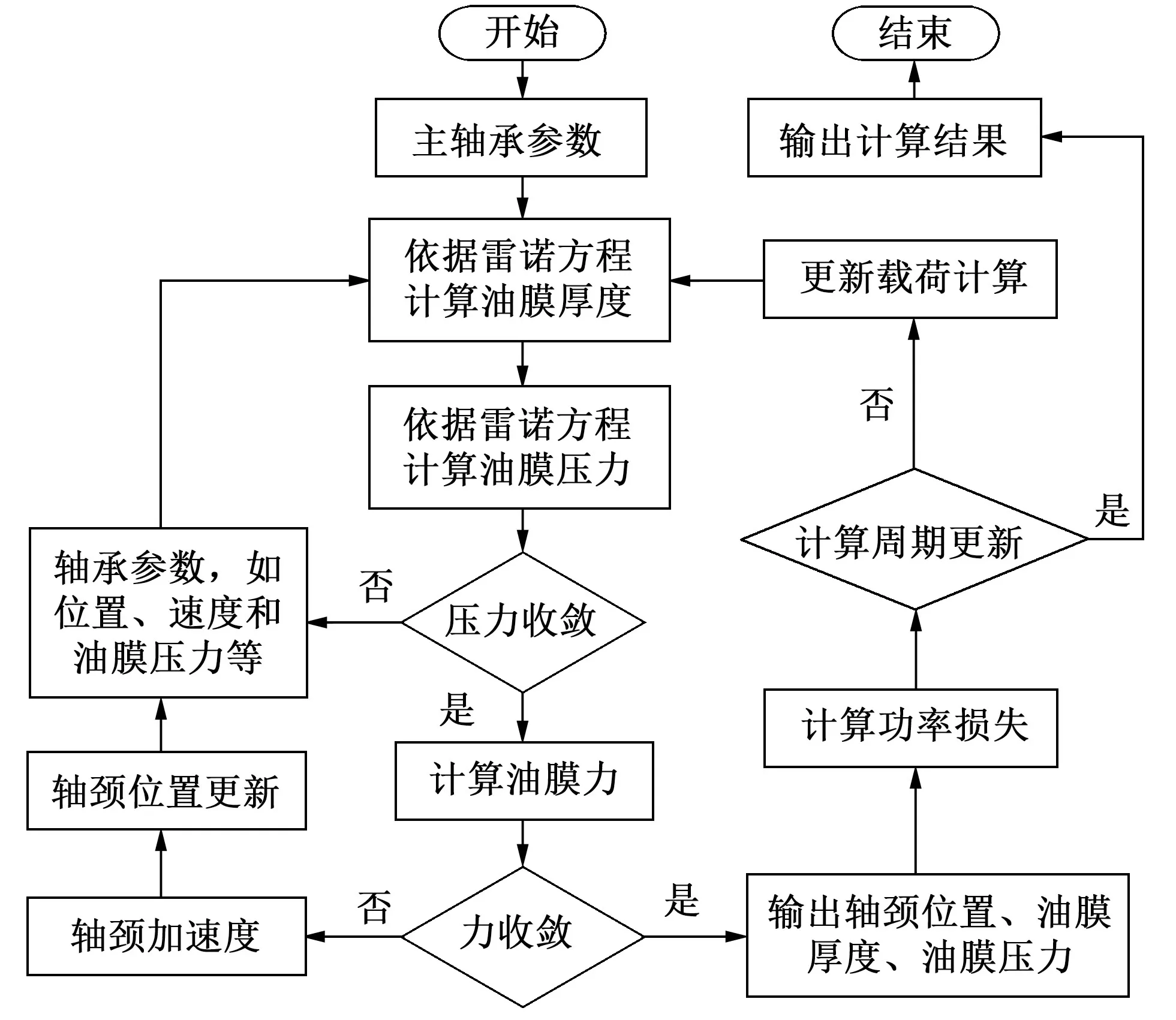
图2 主轴承计算流程图Fig.2 Calculation flowchart of the main bearing

3 仿真结果与分析

为了保证仿真分析结果的准确性和可比性，每个计算工况都连续计算多个周期直至轴承运转平稳，选取平稳工况时的数据作为最终计算结果，从而保证分析模型的准确性；分析中，将不同轴承载荷、不同轴承间隙和不同进油温度作为变量分别进行组合计算，每次计算只改变1个变量，其他变量保持不变，保证每个计算结果只对应1个变量，进而确保仿真结果的可比性。

主轴承的润滑性能主要通过分析轴承的油膜压力、油膜厚度、轴承温度和摩擦功率损失来进行，分析中考虑了计入热效应的曲轴主轴承润滑性能的影响因素。

3.1 最大油膜压力

曲轴主轴承油膜压力随时间呈周期性变化，随着曲轴的转动，每一曲轴转角位置的轴承载荷都会随着轴承外部载荷的变化而变化，每一曲轴转角位置都可以找到与之对应的最大油膜压力，最大油膜压力反映了主轴承能提供的最大油膜载荷。图3所示为主轴承在载荷1 工况、轴承间隙0.03 mm 和进油温度60 ℃时，1 个稳定工作周期内主轴承最大油膜压力随曲轴转角的变化曲线，计算结果分别考虑了计入热效应和不计入热效应两种情况。图4 所示为计入热效应的主轴承在载荷1～载荷3、轴承间隙0.03～0.07 mm、进油温度从0～120 ℃变化时的最大油膜压力变化规律。

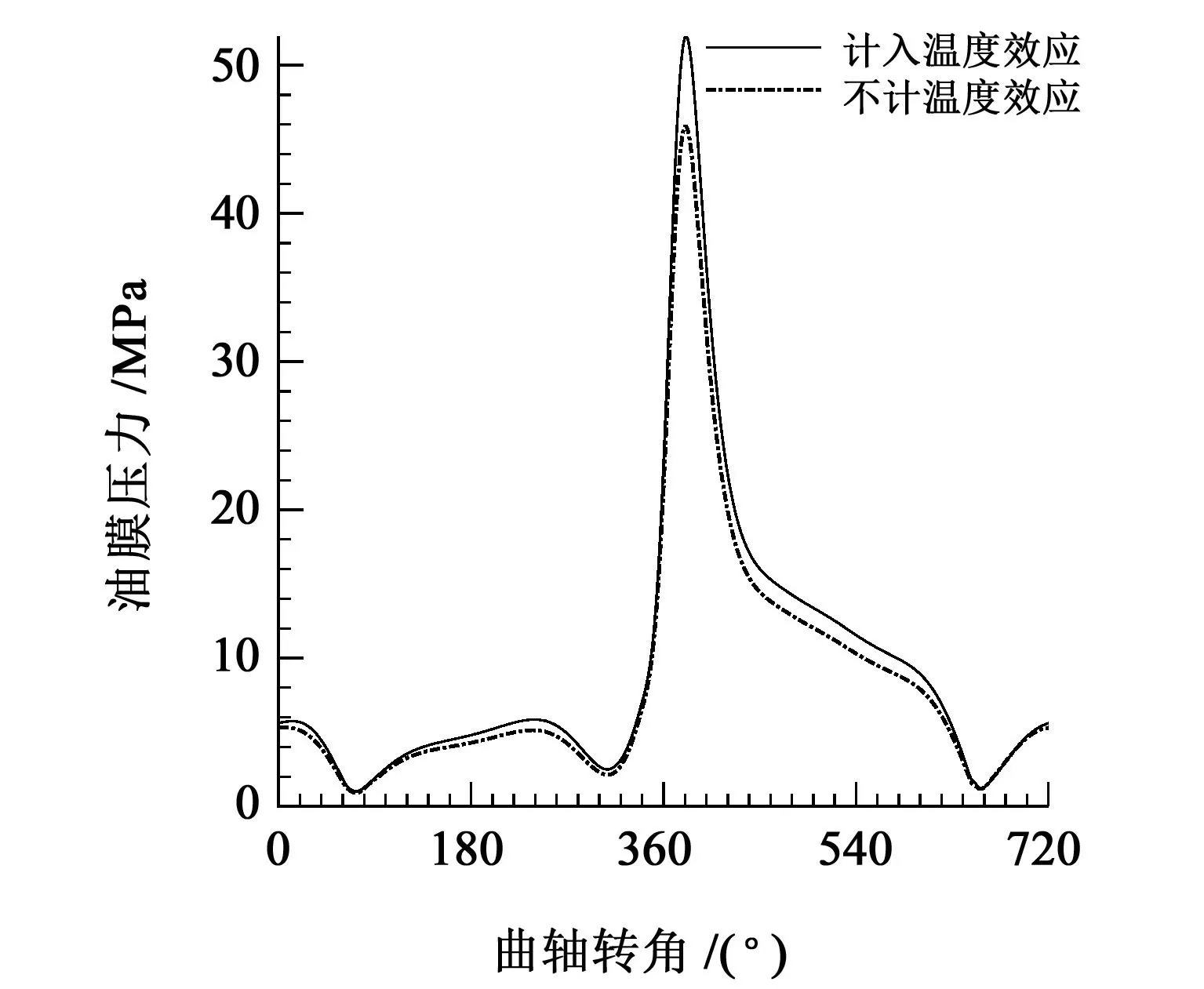
图3 主轴承最大油膜压力对比曲线（载荷1、轴承间隙0.03 mm、进油温度60 ℃）Fig.3 Comparison curve of maximum oil film pressure of the main bearing(load 1,bearing clearance 0.03 mm,oil inlet temperature 60 ℃)

由图3中可以看出，在相同外部载荷条件下，计入热效应的主轴承最大油膜压力为51.94 MPa，不计入热效应的主轴最大油膜压力为45.89 MPa，二者最大值相差13.18%，表明热效应对主轴承最大油膜压力有很大影响，计入热效应时，主轴承最大油膜压力会有增大趋势。由图4 中可以看出，计入热效应时，主轴承最大油膜压力随着进油温度的升高而增大；随着外部载荷的增大，主轴承的最大油膜压力也会增大；在相同载荷作用下，随着轴承间隙的逐步增大，最大油膜压力也相应增大。油膜压力增大，轴承结构强度应相应增加，否则主轴承故障率会增大。因此，为降低主轴承故障率，在相同主轴承结构尺寸和轴承外部载荷的条件下，主轴承的进油温度和轴承间隙都不应过大。

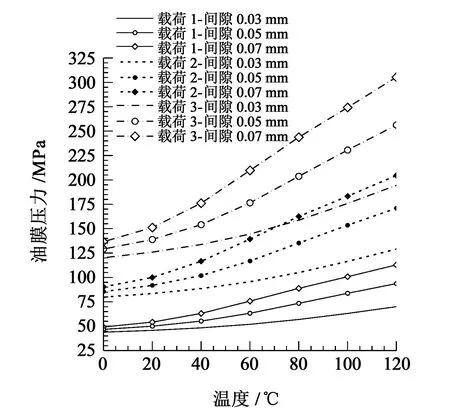
图4 不同工况下主轴承最大油膜压力变化规律对比曲线Fig.4 Comparison curve of variation law of maximum oil film pressure of the main bearing under different working conditions

3.2 最小油膜厚度

曲轴主轴承在1个工作周期内，通过调整轴颈位置来改变油膜的承载载荷大小，主轴颈的位置会随着轴承外部载荷的变化而不断变化。轴颈在每个工作位置都会有一个最小油膜厚度，最小油膜厚度出现的位置也是主轴承工作最容易发生失效的位置。因此，通过确定轴承最小油膜厚度可以判断轴承是否会发生失效。图5所示为主轴承在载荷1工况、轴承间隙0.03 mm 和进油温度60 ℃时，1 个稳定工作周期内主轴承最小油膜厚度随着曲轴转角的变化曲线，计算结果分别考虑了计入热效应和不计入热效应两种情况。图6所示为计入热效应的主轴承在载荷1～载荷3、轴承间隙0.03～0.07 mm 和进油温度从0～120 ℃变化时的最小油膜厚度变化规律。

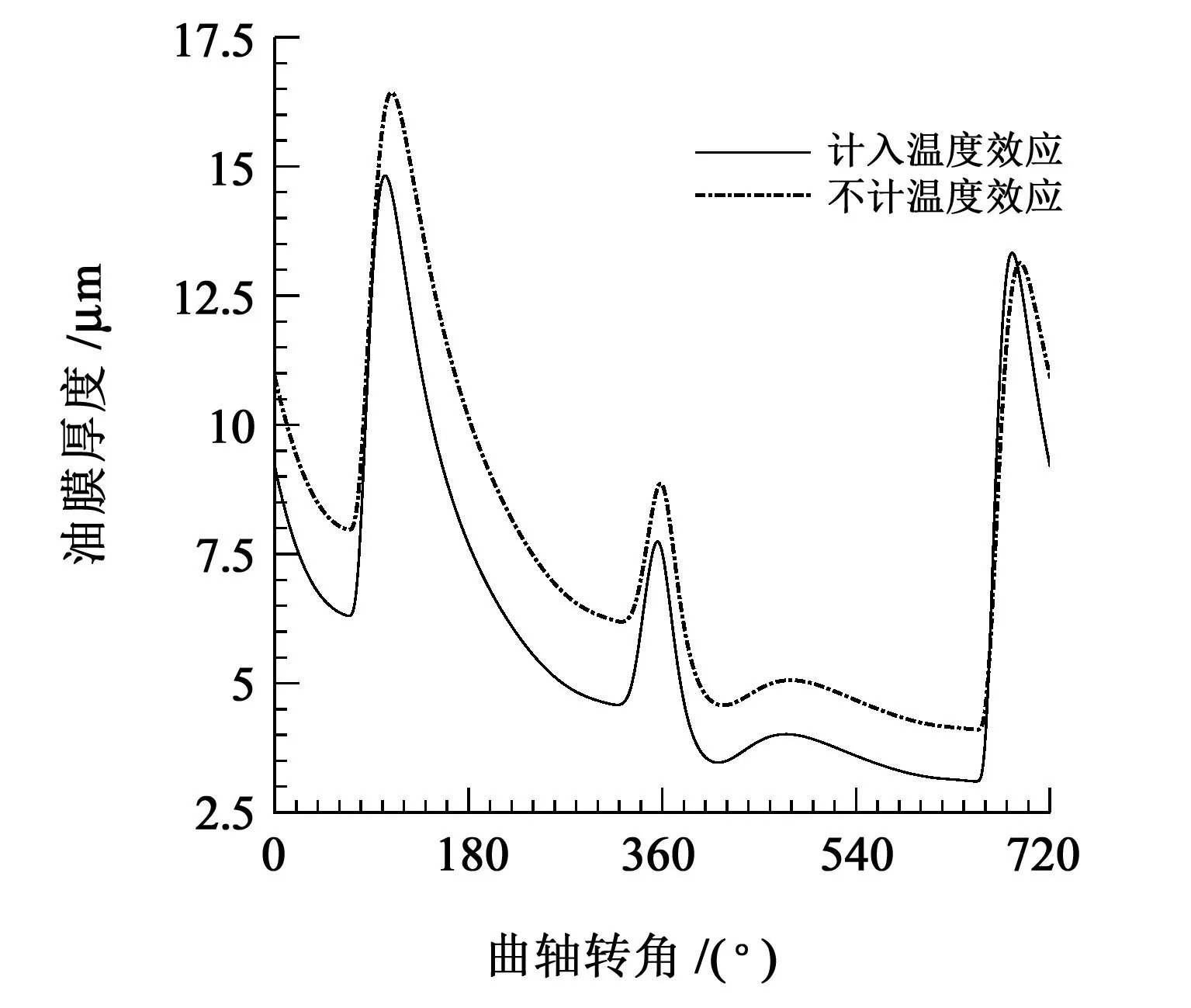
图5 主轴承最小油膜厚度变化曲线（载荷1、轴承间隙0.03 mm、进油温度60 ℃）Fig.5 Variation curve of minimum oil film thickness of the main bearing（load 1,bearing clearance 0.03 mm,oil inlet temperature 60 ℃）

由图5中可以看出，计入热效应和不计入热效应的主轴承最小油膜厚度有明显区别，计入热效应和不计入热效应时的最小油膜厚度分别为3.1 μm 和4.1 μm，这表明在热效应的影响下，相同载荷工况下的主轴承最小油膜厚度会减小。由图6 中可以看出，计入热效应时，主轴承的最小油膜厚度随着轴承进油温度的增加而变小；在相同轴承间隙条件下，随着轴承外部载荷的增加，轴承最小油膜厚度变小；在相同载荷条件下，当进油温度小于70 ℃时，轴承间隙增大，最小油膜厚度会增大，且最小油膜厚度变化较大；当进油温度大于70 ℃时，轴承间隙增大，最小油膜厚度会减小，且最小油膜厚度变化基本接近。最小油膜厚度出现的位置是轴承最容易发生失效的位置，通过对比可以发现，较高的进油温度会造成油膜厚度变小，对主轴承的工作有直接影响。

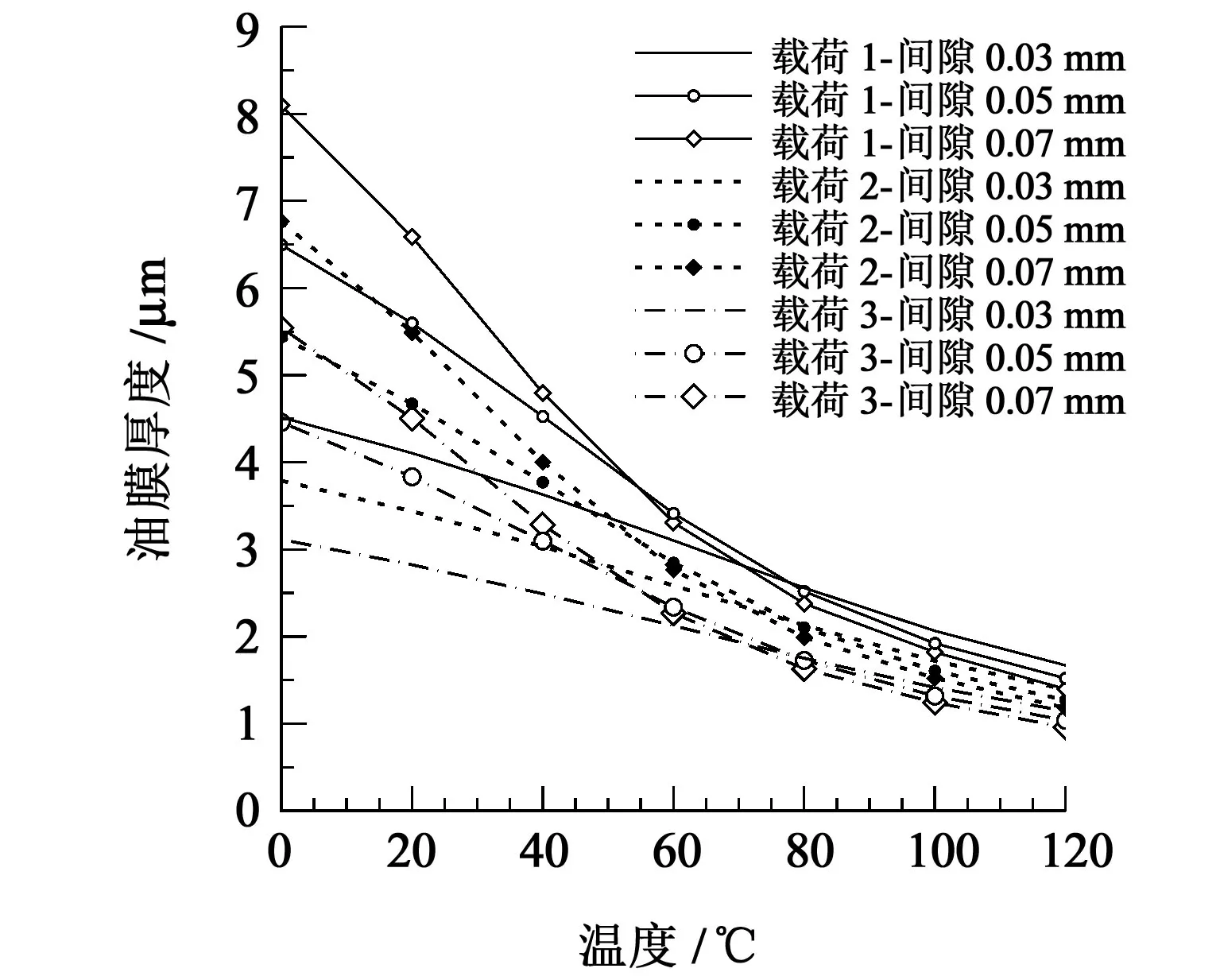
图6 不同工况下主轴承最小油膜厚度变化规律对比曲线Fig.6 Comparison curve of variation law of minimum oil film thickness of the main bearing under different working conditions

3.3 轴承温度

润滑油在主轴颈和主轴承之间形成一层油膜，润滑油膜的温度在外部载荷、剪切力和摩擦力的作用下会发生变化；随着温度的改变，润滑油的黏度和润滑状态都会发生改变，最终会影响整机的工作状态。由于主轴承工作条件恶劣，且受到轴承结构的影响，主轴承的温度测量相当困难。因此，采用仿真方法对主轴承温度进行预测是分析主轴承润滑性能的重要手段。图7 所示为主轴承在载荷1 工况、轴承间隙0.03 mm 和进油温度60 ℃时，1 个稳定工作周期内主轴承润滑油温度随曲轴转角变化的曲线，计算结果分别考虑了计入热效应和不计入热效应两种情况。图8 所示为计入热效应的主轴承在载荷1～载荷3、轴承间隙0.03～0.07 mm 和进油温度从0～120 ℃变化时的最高温度变化规律。

由图7 中可以看出，在进油温度同为60 ℃时，计入热效应的轴承在稳定工作时的温度高于75 ℃，且温度随着轴承载荷的变化而变化；不计热效应的轴承温度保持不变，表明热效应会影响轴承正常工作的温度，计入热效应时温度变化量超过25%。从图8中可以看出，轴承最高油膜温度随着进油温度的增加而增大，当进油温度小于80 ℃时，轴承运转平稳后的温度会比进油温度高，表明润滑油温度会在摩擦的作用下增高，当进油温度大于80 ℃时，轴承运转平稳后的温度与进油温度基本接近；主轴承载荷变化时，润滑油的温度变化规律基本接近，表明轴承外部载荷对润滑油的温度影响较小；随着轴承间隙逐渐变小，轴承温度逐步增加，且轴承间隙越小，温度变化量越明显，表明轴承间隙是影响轴承温度变化的主要因素。温度增加，润滑油的黏度会下降，进而会改变轴承润滑性能。因此，从计算数据看，应当适当增加轴承间隙，保证轴承工作温度在合理范围内。

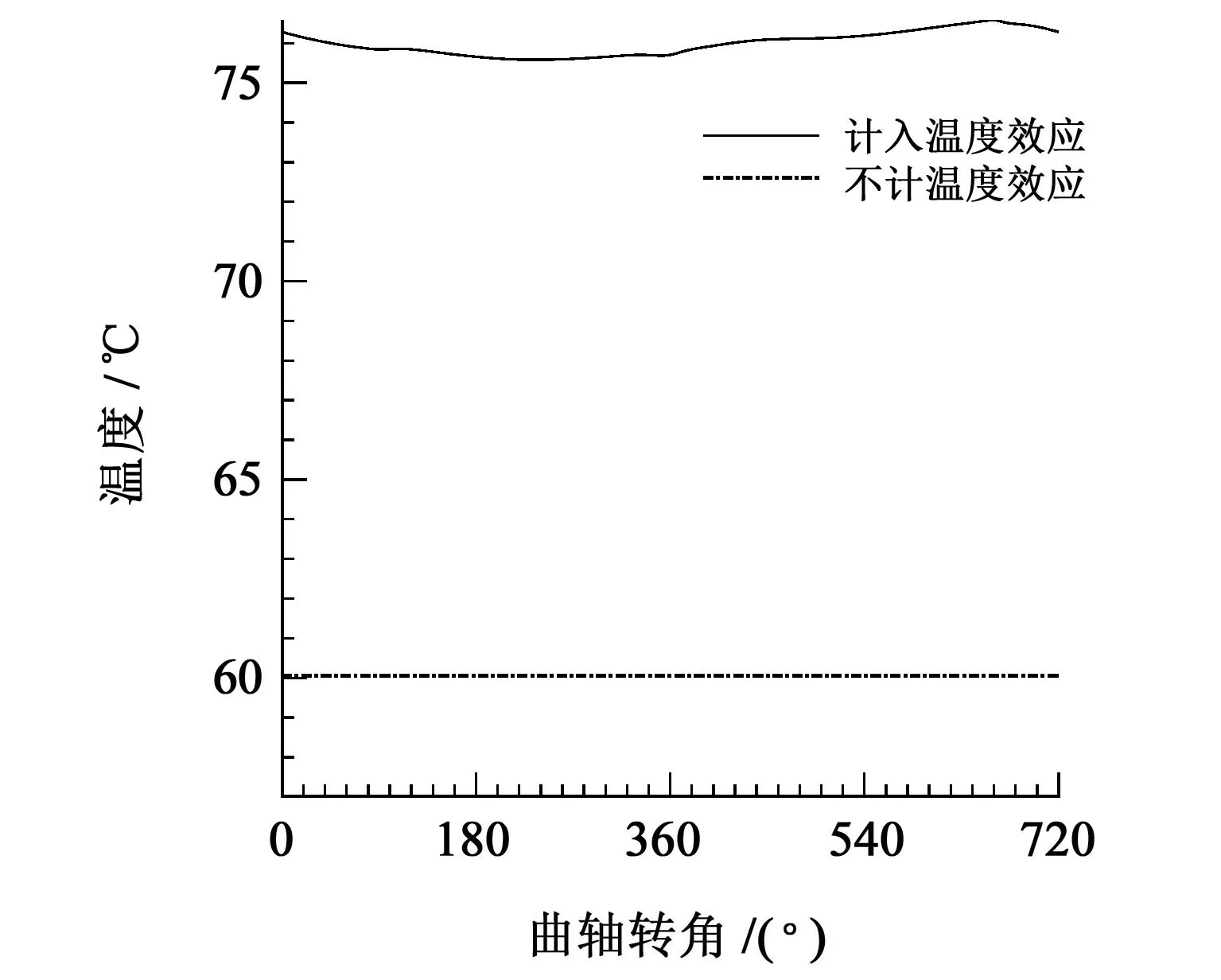
图7 主轴承温度变化曲线（载荷1、轴承间隙0.03 mm、进油温度60 ℃）Fig.7 Temperature variation curve of the main bearing（load 1,bearing clearance 0.03 mm，oil inlet temperature 60 ℃）

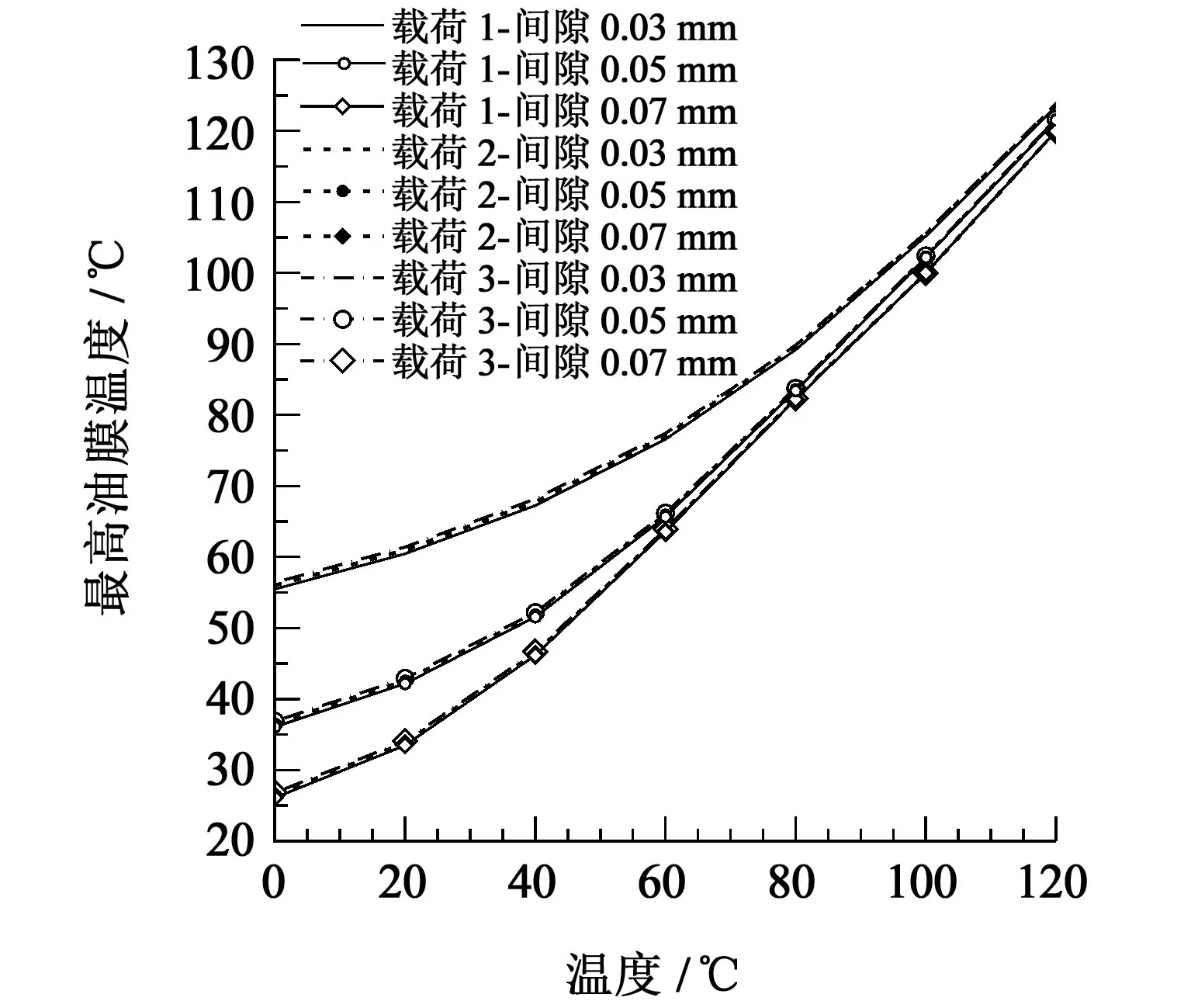
图8 不同工况下主轴承最高温度变化规律对比曲线Fig.8 Comparison curve of maximum temperature variation law of the main bearing under different working conditions

3.4 摩擦功率损失

曲轴主轴承作为典型的滑动摩擦副，是产生摩擦功率损失的主要零部件。功率损失虽然不可避免，但是可以通过合理选择设计参数，有效降低功率损失，达到提高内燃机工作效率的目的。图9所示为主轴承在载荷1 工况、轴承间隙0.03 mm 和进油温度60 ℃时，1个稳定工作周期内主轴承摩擦功率损失随着曲轴转角变化的曲线，计算结果分别考虑了计入热效应和不计入热效应两种情况。图10 所示为计入热效应的主轴承在载荷1～载荷3、轴承间隙0.03～0.07 mm和进油温度从0～120 ℃变化时的最大摩擦功率损失变化曲线。

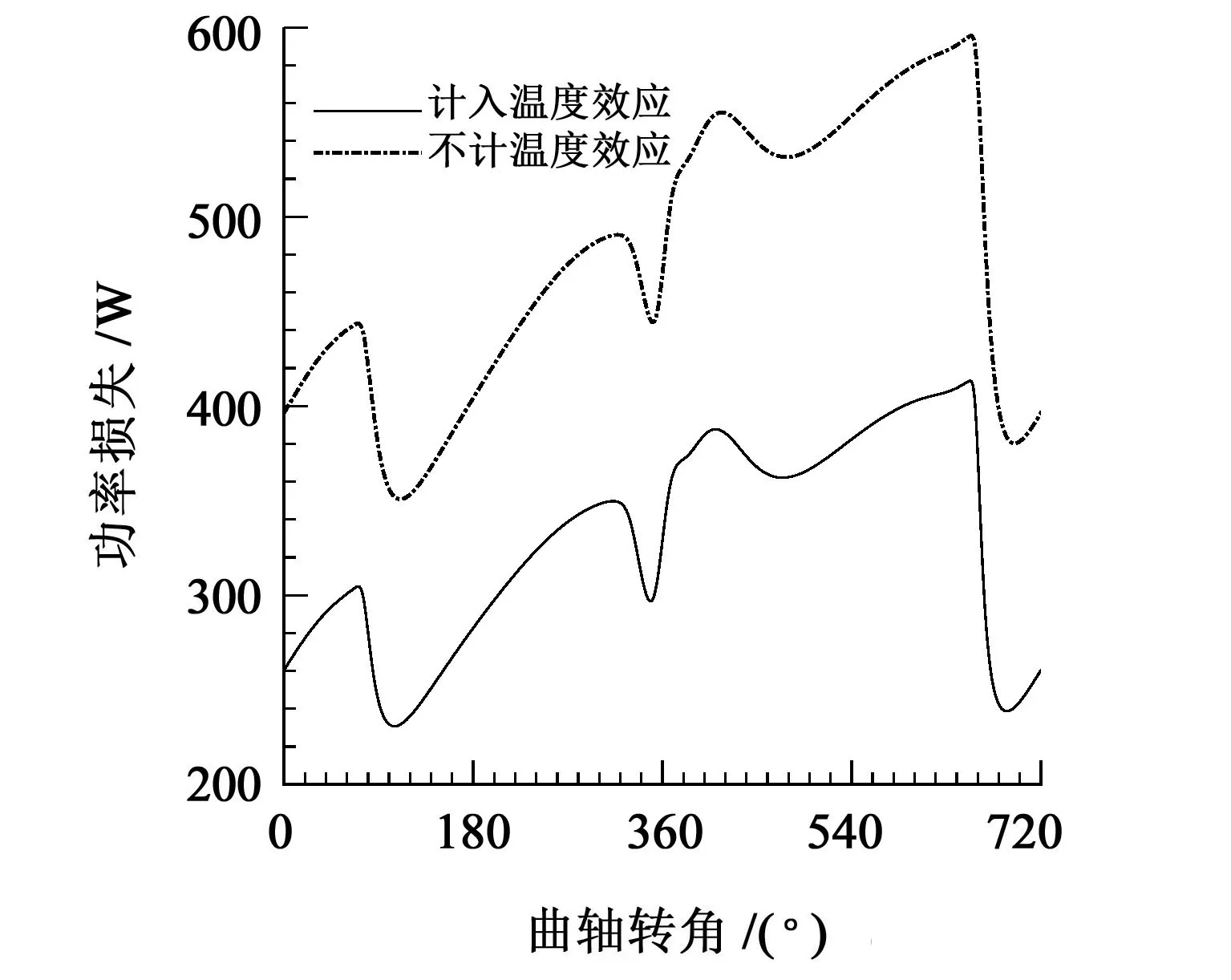
图9 主轴承摩擦功率损失变化曲线（载荷1、轴承间隙0.03 mm、进油温度60 ℃）Fig.9 Variation curve of friction power loss of the main bearing（load 1,bearing clearance 0.03 mm,oil inlet temperature 60 ℃）

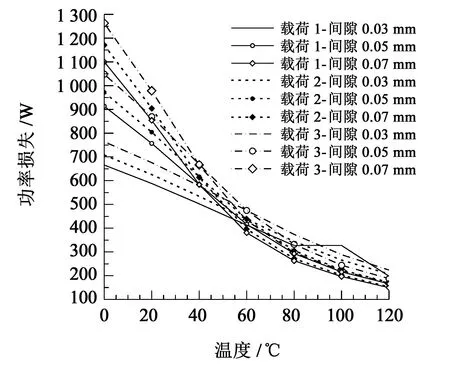
图10 不同工况主轴承最大摩擦功率损失对比曲线Fig.10 Comparison curve of maximum friction power loss of the main bearing under different working conditions

从图9中可以看出，在同样边界条件下，计入热效应的轴承最大摩擦功率损失为400 W，不计入热效应的轴承最大摩擦功率损失为600 W，二者最大值相差50%，表明计入热效应时的轴承摩擦功率损失下降，其原因是计入热效应时，润滑油温度上升，导致润滑油的黏度下降，最终导致轴承摩擦功率损失下降。由图10 中可以看出，轴承的最大摩擦功率损失会随着进油温度的增加而减小；相同轴承间隙条件下，随着轴承外部载荷的增大，轴承最大摩擦功率损失也会随之增大；当轴承间隙发生变化时，进油温度会影响最大摩擦功率损失；进油温度在40～60 ℃时，不同间隙的润滑油最大摩擦功率损失变化规律会发生改变，当进油温度小于该温度范围时，轴承间隙变大，最大摩擦功率损失会增大，当进油温度高于该温度范围时，轴承间隙变小，最大摩擦功率损失会增大。