例析构造函数法证明不等式的六种策略
2022-10-10江苏省金湖中学211600
中学数学研究(江西) 2022年9期
江苏省金湖中学 (211600) 刘 金
运用对相关函数求导证明不等式是近年来高考命题的一类热点题型,由于涉及许多导数问题中的解题技法,降低了解题的成功率,我们有不少同学都望而却步.此类问题的破题关键就是构造一个与待证不等式紧密联系的函数,然后运用导数运算的方法,研究该函数的单调性、极值、值域等性质,进而达到证明不等式的目的.本文以近几年高考题或模拟题为例,通过探索不同类型不等式的证明,阐述构造函数证明不等式的六种思考,供参考.
一、移项作差构造函数
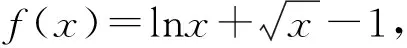
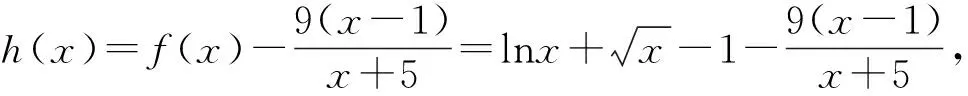
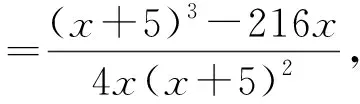
评注:移项作差法是证明不等式的最常用的方法,而构造新函数是利用导数解决问题的重要手段,本题中,在导函数式大小时根据解题需要又采用了放缩的办法,并且再一次构造函数,最后才确定了大小关系,是一个难度相对较大的题目.
二、增添项后构造函数
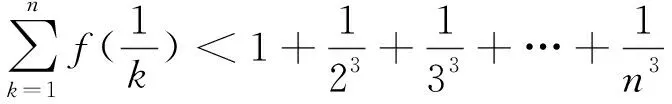
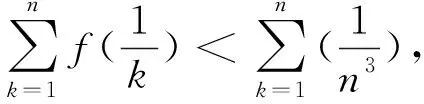
评注:通过将待证的结论式变形整理,揭露了待证式的实质,也就是需要证明不等式f(x) 评注:在本题中,由于是证明两个变量的大小关系问题,通过换元,将两元变换成一元,这样降低了问题的难度,使之变成我们熟悉的、容易解决的问题了. 评注:在充分挖掘题目内涵的基础上,将待证的不等式进行转化、变形,使之等价变形为另一个大小关系证明的问题,然后再通过建立新函数轻松地解决了问题. 评注:由于待证的不等式比较复杂,在分析、化简、变形的基础上,再经过换元处理,成功的找到同构关系,进而设新函数,成功地解决问题. 评注:根据解题需要,对表达式中的一部分采用构造函数处理,也是一个重要的解题思路,这种求解方法的关键是精确替换,以起作用、易解决为替换原则.三、及时换元后构造函数
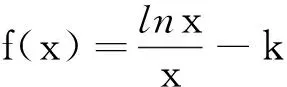
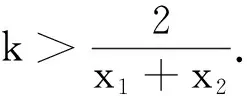
四、等价转化后构造函数
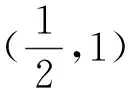
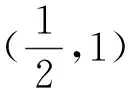
五、挖出同构关系后构造函数
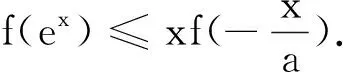
六、选择关键部分构造函数