隔板法解一类不定方程整数解的组数问题
2022-10-10浙江省嘉善第二高级中学314100鲁和平
浙江省嘉善第二高级中学 (314100) 鲁和平
高中学生在学习排列组合时,都会学习如何用隔板法解题,从而不可避免地遇到不定方程整数解的组数问题.由于此类问题变化很多,情形复杂,学生往往似懂非懂.如果我们从最简单的情形入手,拾级而上,环环相扣,就会掌握其内在规律.
一、回归原点
例1 方程x1+x2+x3+x4=12共有多少组正整数解?
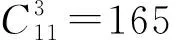
评注:本题是隔板法最原始最基本的模型.把握两个必要条件:一是相同的元素,二是被隔板隔开的每一部分数目不小于“1”.充分理解这个模型,其它的类似问题迎刃而解.
二、迈开小步
例2 方程x1+x2+x3+x4=12共有多少组非负整数解?

评注:由“非负整数解”向“正整数解”过渡,只需换元.虽说只迈开了小小的一步,但给人的启发很大,后续变形都是稍作调整,如法炮制.
三、变更范围
例3 方程x1+x2+x3+x4=12满足“x1≥-1,x2≥3,x3≥-2,x4≥2”的整数解共有多少组?

评注:此题变形,只需把每个未知数的范围变为“大于等于1”就行了.突破此关,势如破竹.
四、变换关系
例4 方程x+y+z=2011满足x 评注:本题增加了限制条件“x 例5 方程x1+x2+…+x99+2x100=3的非负整数解共有多少个? 评注:原来的不定方程的各个未知数系数均为“1”.本题虽说将x100的系数作了微调,但带来的影响是巨大的.分类讨论是主要办法.重在对排列数公式及组合数公式的深刻理解. 例6 求不定方程x1+x2+x3+3x4+3x5+5x6=21的正整数解的组数(2009年湖北省预赛第10题). 解:原方程即为(x1+x2+x3)+3(x4+x5)+5x6=21,令x1+x2+x3=x,x4+x5=y,x6=z,则x≥3,y≥2,z≥1.先考虑不定方程x+3y+5z=21满足x≥3,y≥2,z≥1的正整数解.因为x≥3,y≥2,z≥1,所以5z=21-x-3y≤12,则1≤z≤2. ①当z=1时,有x+3y=16,此方程满足x≥3,y≥2的正整数解为(x,y)=(10,2),(7,3),(4,4); ④当x1=3时,方程x2+x3+x4+x5=1的非负整数解的个数为4. 评注:除了变更不定方程各个未知数的系数,还可以变更未知数的幂.本题试着将x1的幂由“1”变为“2”.解决的办法是“分类讨论+隔板法”. 综上几例可见,不定方程整数解的组数求解问题是非常复杂的.本文只是例举了求解中常见的几种变更形式,但远未能窥全豹,也不可能得出一般性的结论.更多的是需要我们有“遇山劈路遇水架桥”的随机应变的能力.
五、变更系数




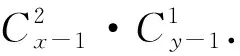
六、变更形式