对一道模考题的多解探究与通法总结

安徽省芜湖市第一中学 (241000) 刘海涛

《高考评价体系》指出：高考要从“知识立意”转向“能力立意”，考查学生的“关键能力”和“核心素养”.这就要求学生在学习中，学会灵活运用所学知识分析、解决问题，达到从“解题”向“解决问题”的转变.在解析几何问题中，有一类问题结构上为关于两变量(x1,x2或y1,y2)的非对称结构，无法直接利用韦达定理代入计算，如何处理呢？笔者从一道模考题出发，总结该类问题的常见模型，并给出处理策略，以帮助读者在高考备考中掌握该类问题的模式化解题策略，现与读者交流.

1 问题呈现与分析

题1 已知圆O：x2+y2=8，点M,M′的坐标分别为(2,0),(-2,0)，以MN为直径的圆内切于圆O，记点N的轨迹为曲线C.

(1)求曲线C的方程；

2 解法探究

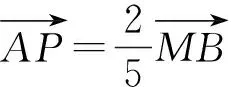
3 通性通法的总结

通过上述解答，我们初步了解了对于一类非对称型结构的处理方法，笔者通过阅读文献[1],发现其对该类问题的总结仍不够全面，现笔者将圆锥曲线中常见的关于变量(x1,x2或y1,y2)的非对称型结构，及其处理策略总结如下.

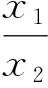
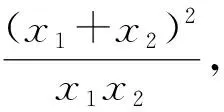
类型2 对于px1+qx2+r=0(p≠q)的结构，有以下五种处理策略：

①直接利用方程的求根公式得出x1,x2，代入计算；

②结合韦达定理的两根和表达式，联立方从解出x1,x2，再代入两根积式计算；

③综合方法①和②，将关于x1的两个表达式联立成等式；

4 变式迁移

(1)求椭圆C的方程；

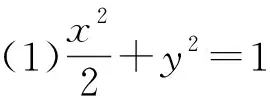
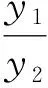
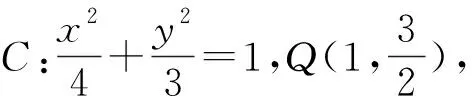
5 反思总结

5.1 一题多解，提高解题能力

5.2 总结通法，形成模式化解题策略

通过分析、对比、归纳，概括出一类问题的共同特点，依此特点制定规范的解题步骤，形成模式化解题策略，这样就可以教会学生处理同类问题的通解通法，避免题海战术，减轻学业负担，提高学习效率[3].笔者总结了解析几何中常见的三类非对称结构，对于类型1，构造倒数和加2的表达式，即可得到对称式；对于类型2，总结了5种处理策略，前3种策略起点低但运算量大，后两种思维起点高，技巧性强，但运算量小；对于类型3，仔细观察“x1+x2”与“x1x2”的结构，配凑出两者间的恒等式，代入即可得到结果.通过变式问题的训练，将方法进行迁移，强化一类典型问题的模式化解题思维，这样，我们在学习基础知识，掌握基本技能的同时，可以有效锻炼思维的深刻性、广阔性、灵活性和创新性，达到举一反三、融会贯通的解题水平和能力，提高自身的数学思想和数学核心素养[4].