求解圆锥曲线中定值问题的若干策略

上海市控江中学 (200433) 孙雷鸣

解析几何中的定值问题是高考命题的一个热点，也是解析几何问题中的一个难点，在求解过程中往往伴随着一定的解题技巧和较为复杂的运算.在学习中如果能加强解决此类问题的方法总结，可提高探究数学问题的兴趣，并能提升思维能力，掌握更多的解题技能，为应付各类考试积累更多的能量.本文通过对典型例题的分析探求，阐述圆锥曲线中定值问题求解的常用策略，仅供读者朋友参考.

一、引参用参

在解析几何问题中，待定系数法是最基本的解题方法，即通过设参数，利用参数表示曲线方程、建立等量关系、进行运算化简，直到最后达到解题目的.

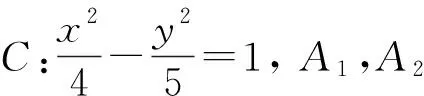
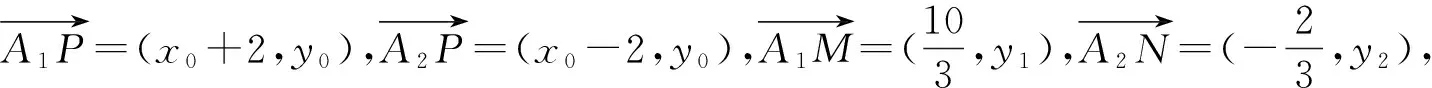
评注：解题中通过运用向量共线的性质，抓住双曲线上点参数x0，y0来表示动参数y1、y2，并表示出向量数量积是解题题的关键，设参数是方便列式，而消参就是解题的目的.

二、利用方程

在圆锥曲线问题中，灵活的运用曲线方程是非常重要的，这里何时用、怎样用要把握好机会，点在曲线上是一个运用信号，一般情况下，整体运用比较多见.

评注：通过设动点P(x0,y0)，然后运用点参数表示出平行四边形的面积后，再利用点在曲线上这个重要条件进行整体消元，这是设点而不求点，整体求解的典型用法.

三、活用中点

解析几何中的中点也是一个非常有用的几何概念，对它进行合理的利用可发挥出重要的作用，比较突出的是配合“韦达定理”的使用.

例3 过抛物线y2=8x的焦点F作倾斜角为锐角α的直线l与抛物线交于A、B两点，AB的垂直平分线m交x轴于点P，求证：|FP|-|FP|cos2α为定值.

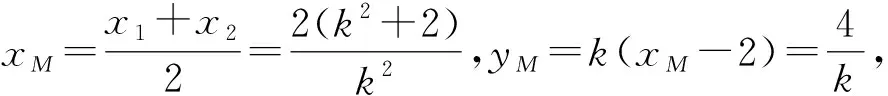
评注：在题设中捕捉到了中点的条件，并通过方程联立将中点表示出来，是成功解题的关键.

四、整体运算

在解析几何问题中，一般都有很多的字母运算，如果再设点、斜率等参数，则表达式可能更为复杂，这里我们必须条理清楚、设而不求、整体求解，直至一次成功.

评注：题目要求|AN|·|BM|，通过分别用参数将两个距离|AN|、|BM|表示出来，然后再对它们的积的表达式整体代入、整体化简，这是解析几何考题的一个重要考核目标.

本文介绍的是比较常用的求解思路，在具体解题过程中，根据已知条件和待求结论还会有许多适用的方法，其解题核心就是抓住特点、顺势而为，同学们可以学习中积累经验.