作差法在求数列通项公式中的功效

◇　甘肃　田　广

(作者单位：甘肃省武山县马力中学)



作差法在求数列通项公式中的功效

◇甘肃田广

当遇到含有前n项和Sn或若干项和的数列题目时,我们经常通过将和式少写或者多写1项,再将二者整体相减,只剩下第n项或n-1项,这样就得到相应的递推关系式,从而问题转化为已知递推关系求数列通项问题.但有时得不到我们想要的递推公式,怎么办?再作差,直到得到我们想要的关系式．

1　1次作差可将多余项的干扰整体消除

2　2次作差可以获得相邻2项的递推关系

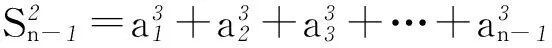
2式相减,得

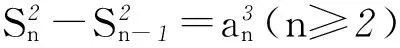
即

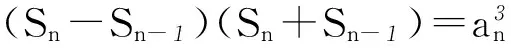
所以

化简得

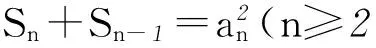
又

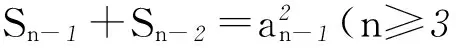
3　明确目标尽显“作差”的奇特效果

3Sn-1=nan-1+n(n-1)(n≥2).

2式相减,得

nan-1=(n-2)an+2n(n≥2),

(n-1)an-2=(n-3)an-1+2n-2(n≥3).

2式相减,得

(2n-3)an-1=(n-2)an+(n-1)an-2+2(n≥3).

尝试构造数列,得

(n-2)an-1+(n-1)an-1=(n-2)an+(n-1)an-2+2.

适当调整,得

(n-1)(an-1-an-2)=(n-2)(an-an-1)+2,

(n-2)(an-2-an-3)=(n-3)(an-1-an-2)+2.

2式相减,得

(2n-4)(an-1-an-2)=

(n-2)(an-an-1)+(n-2)(an-2-an-3),

化简,得

2(an-1-an-2)=(an-an-1)+(an-2-an-3)(n≥4),

所以数列{an-an-1}是等差数列,且an-an-1=a2-a1=6-2=4,所以an=2+(n-1)4=4n-2．

(2n-4)(an-1-an-2)=

(n-2)(an-an-1)-(n-2)·(an-2-an-3),

即2(an-1-an-2)=(an-an-1)+(an-2-an-3).根据等差中项可以判断数列{an-an-1}是等差数列．本题虽然是经历3次作差,但是每次作差都有目的和方向,并不是盲目作差．

(作者单位：甘肃省武山县马力中学)