基于展向波纹穿孔结构的受电弓杆件减阻降噪研究
2022-10-05张长亮
张长亮
(郑州地铁集团有限公司,河南 郑州 450000)
地铁列车受电弓位于列车顶部,由多个杆件组成,列车在隧道中行驶会产生显著的气动噪声。由于列车顶部的防护隔离手段有限,受电弓气动噪声污染对市民造成了严重影响。近年来,国内外针对受电弓气动特性、气动噪声的研究取得了一定进展。张亚东等通过风洞实验模拟分析得出,受电弓产生的气动噪声集中在迎风侧区域的弓头、底架、绝缘子等部件中[1]。Bearman和Owen发现,受电弓迎风面上展向波纹的波长和振幅对减阻降噪具有重要作用[2]。刘海涛等研究发现,λ/D=2、ω/D=0.48的受电弓弓头展向波纹结构模型杆件对于降低气动噪声具有明显的效果,且与风洞实验的结果有着良好的一致性[3]。展向波纹结构对于降低气动噪声具有一定效果,但受电弓弓头展向波纹穿孔结构特性与降噪性能的关系还缺乏深入研究。
本研究对λ/D=2、ω/D=0.48的展向波纹结构模型进行波峰、波谷、波峰波谷耦合穿孔优化设计,并通过流体计算软件FLUENT进行流场的稳态和瞬态计算求解,以及ACTRAN声学网格计算获取气动噪声声源及传播过程。对考察范围内的受电弓弓头展向波纹穿孔结构模型进行优化分析,并研究其减阻降噪机理。
1 计算理论及方法
1.1 流体流动的控制方程
对受电弓弓头展向波纹穿孔结构模型的周围流场进行数值仿真,模拟地铁列车的运行速度,由于气流流速小于0.3倍马赫数,可认定空气为不可压缩流动。完整的三维N-S方程守恒形式如式(1)。
(1)
式中U、F的表达式如式(2)。
(2)

1.2 宽频噪声模型
采用宽频噪声模型对展向波纹结构杆件稳态计算求解。宽频带噪声模型声功率计算公式如式(3)。
(3)
式中,u是湍流速度、l是湍流特征尺度、c0是声速、α为模型常数。
对于湍动能k和湍动能耗散率ε,式(3)可以改写成式(4)形式。
(4)
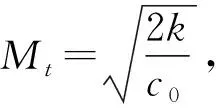
气动噪声声功率级如式(5)。
(5)
式中,Pref是参考声压,取10-12W/m3。
2 研究方法
2.1 弓头展向波纹结构参数化建模
研究表明λ/D=2、ω/D=0.48的展向波纹结构模型降噪性能要优于其他参数模型及直方杆模型。通过对λ/D=2、ω/D=0.48的展向波纹结构模型进行穿孔优化设计,对模型进行三种穿孔方式处理,建立波峰穿孔模型、波谷穿孔模型及波峰波谷穿孔模型。图1为展向波纹模型结构图,其中:D=0.04 m为固定值,是波峰到波谷的振幅;λ为波长,上游最远的横截面称为“峰”,下游最远的横截面称为“谷”。在Creo中对λ/D=2、ω/D=0.48的展向波纹结构模型进行穿孔设计,在波峰建立截面为12 mm×8 mm矩形孔的波峰穿孔模型、在波谷建立截面为8 mm×8 mm矩形孔的波谷穿孔模型,以及两者耦合的波峰波谷穿孔模型,如图2所示。对三种穿孔模型的展向波纹结构模型进行网格划分、流场稳态和瞬态计算求解及远场噪声频谱和指向性分析,并研究其降噪机理。

图1 展向波纹模型结构图

(a)波峰穿孔模型 (b)波谷穿孔模型 (c)波峰波谷穿孔模型
2.2 穿孔结构模型网格划分方法
对弓头展向波纹穿孔结构模型进行网格划分,并建立有限元模型。为了更好分析流场变化,分别在模型周围和尾流区域建立两重密度盒子捕捉流场的变化。进行网格无关性验证,当网格数从880 W增加至950 W时,数值模拟结果误差在4%以内,计算模型的有限元网格总数量为950 W左右。
2.3 流场后处理方法
弓头展向波纹结构流场计算分为稳态和瞬态计算求解。稳态计算模型的入口边界定义为速度入口,模拟仿真地铁列车的运行时速;出口边界定义为压力出口,速度垂直于入口进入,回流湍流强度和黏度比均为1%;噪声模型采用宽频带噪声模型、标准k-ε模型,基于最小二乘单元进行梯度离散,选用二阶迎风的压力离散格式,并选用SIMPLEC算法进行迭代计算。
瞬态计算求解采用大涡模拟,压力速度耦合算法采用Couple算法。计算分析的时间步长为10-4s,共计算500个时间步长数,每20个迭代步数输出一个结果文件,为提高计算精度采样频率设置104 Hz,分析的最高频率为2 000 Hz。
2.4 声场后处理方法
声学软件ACTRAN中,利用离散傅里叶变换将稳态求解的时域信号转换为频域信号;以展向波纹穿孔结构模型为中心,以半径R=1.18 m建立180°的极坐标半圆,以1°为间隔建立180个监测点,如图3所示,通过远场噪声监测点分析弓头展向波纹穿孔结构模型的噪声频谱和声学指向性。

图3 远场噪声监测点
3 降噪分析
模拟地铁列车60 km/h运行速度工况,对弓头展向波纹穿孔结构模型结果进行分析。波峰、波谷和波峰波谷三组穿孔模型在200 Hz下噪声云图的尾流区域均存在明显的卡门涡街现象。其中,靠近杆件模型附近尾流区域的涡旋强烈,而波峰波谷模型的尾流区域范围及幅值都显著低于波峰模型和波谷模型,因而有着更好的气动性能。
分析R=1.18 m测点91处的远场噪声频谱可知:在100~160 Hz、280~360 Hz频率范围内,波峰波谷穿孔模型较波峰穿孔模型和波谷穿孔模型的声压级有所降低;在180~360 Hz、380~480 Hz频率范围内,波谷穿孔模型较波峰波谷穿孔模型和波峰穿孔模型的声压级显著降低;波峰波谷穿孔模型的总声压级较波峰穿孔模型和波谷穿孔模型分别降低了0.51 dB和0.37 dB。
分析R=2 m测点91处的远场噪声频谱可知:在260~440Hz频率范围内,波峰波谷穿孔模型较波峰穿孔模型和波谷穿孔模型的声压级有所降低;在180~260 Hz、380~480 Hz频率范围内,波谷穿孔模型较波峰波谷穿孔模型和波峰穿孔模型的声压级显著降低;在0~2 000 Hz范围内,波峰波谷穿孔、波谷穿孔模型的声压级曲线均低于波峰穿孔模型,波峰穿孔模型的降噪性能要弱于波谷穿孔和波峰波谷穿孔模型;波峰波谷穿孔模型的总声压级较波峰穿孔模型和波谷穿孔模型分别降低了1.46 dB、1.21 dB。
分析R=5 m测点91处的远场噪声频谱可知:在100~200 Hz频率范围内,波峰波谷穿孔模型较波峰穿孔模型和波谷穿孔模型的声压级有所降低;波峰波谷穿孔模型的总声压级较波峰穿孔模型和波谷穿孔模型分别降低了1.43 dB、1.29 dB。
波峰波谷模型气动阻力值较波峰模型、波谷模型分别降低了1.0 N和2.4 N。
分析远场噪声指向性:在0°~135°、172°~175°的辐射角范围内,波峰波谷模型的声压级小于波峰模型和波谷模型;在140°~170°的辐射角范围内,波谷模型的声压级小于波峰模型和波峰波谷模型;在辐射角88°附近,波峰波谷模型的辐射声压级最小。
4 结论
(1)展向波纹波峰穿孔结构模型在远场R=1.18 m、2 m、5 m处的总声压级较λ/D=2、ω/D=0.48的展向波纹结构模型分别降低了0.82 dB、0.91 dB和0.89 dB;
(2)展向波纹波谷穿孔结构模型在远场R=1.18 m、2 m、5 m处的总声压级较λ/D=2、ω/D=0.48的展向波纹结构模型降低了0.96 dB、1.16 dB和1.03 dB;
(3)展向波纹波峰波谷穿孔结构模型在远场R=1.18 m、2 m、5 m处的总声压级较λ/D=2、ω/D=0.48的展向波纹结构模型降低了1.33 dB、2.37 dB和2.32 dB;
(4)展向波纹波峰波谷穿孔结构模型气动阻力值较波峰穿孔模型、波谷穿孔模型分别降低了1.0 N和2.4 N;
(5)展向波纹波峰波谷穿孔结构模型在远场R=1.18 m、2 m、5 m处的总声压级较波峰穿孔模型分别降低了0.51 dB、1.46 dB和1.43 dB,波谷穿孔模型分别降低了0.37 dB、1.21 dB和1.29 dB;
(6)在0°~135°、172°~175°的辐射角范围内,展向波纹结构波峰波谷穿孔模型的声压级小于波峰穿孔模型和波谷穿孔模型,在140°~170°的辐射角范围内,展向波纹结构波谷穿孔模型的声压级小于波峰穿孔模型和波峰波谷穿孔模型,在辐射角88°附近展向波纹结构波峰波谷穿孔模型的辐射声压级最小。
5 结语
地铁快速发展的同时提升乘车品质尤为重要,降噪研究不可忽视。本研究从受电弓弓头降噪出发,对λ/D=2、ω/D=0.48的展向波纹结构模型进行穿孔优化设计,研究表明受电弓弓头展向波纹结构波峰波谷穿孔模型对于降低气动噪声具有一定作用,为地铁电客车在区间隧道行驶减阻降噪提供一定的理论依据。
