Dynamic Loads and Wake Prediction for Large Wind Turbines Based on Free Wake Method
2015-11-24CaoJiufa曹九发WangTongguang王同光LongHui龙慧KeShitang柯世堂XuEofeng许波峰
Cao Jiufa(曹九发)'Wang Tongguang(王同光)' Long Hui(龙慧)'Ke Shitang(柯世堂)'Xu Eofeng(许波峰)
1.Jiangsu Key Laboratory of Hi-Tech Research for Wind Turbine Design' Nanjing University of Aeronautics&Astronautics'Nanjing 210016'P.R.China;
2.Department of Mechanical Engineering'The University of Sheffield'Sheffield S1 3JD'UK
Dynamic Loads and Wake Prediction for Large Wind Turbines Based on Free Wake Method
Cao Jiufa(曹九发)1'2'Wang Tongguang(王同光)1*' Long Hui(龙慧)2'Ke Shitang(柯世堂)1'Xu Eofeng(许波峰)1
1.Jiangsu Key Laboratory of Hi-Tech Research for Wind Turbine Design' Nanjing University of Aeronautics&Astronautics'Nanjing 210016'P.R.China;
2.Department of Mechanical Engineering'The University of Sheffield'Sheffield S1 3JD'UK
With large scale wind turbines'the issue of aerodynamic elastic response is even more significant on dynamic behaviour of the system.Unsteady free vortex wake method is proposed to calculate the shape of wake and aerodynamic load.Considering the effect of aerodynamic load'inertial load and gravity load'the decoupling dynamic equations are established by using finite element method in conjunction of the modal method and equations are solved numerically by Newmark approach.Einally'the numerical simulation of a large scale wind turbine is performed through coupling the free vortex wake modelling with structural modelling.The results show that this coupling model can predict the flexible wind turbine dynamic characteristics effectively and efficiently.Under the influence of the gravitational force'the dynamic response of flapwise direction contributes to the dynamic behavior of edgewise direction under the operational condition of steady wind speed.The difference in dynamic response between the flexible and rigid wind turbines manifests when the aerodynamics/structure coupling effect is of significance in both wind turbine design and performance calculation.
wind turbine;free wake method;aerodynamic dynamics;structural dynamics
0 Introduction
Large scale wind turbines operate in complicated conditions'which contain all kinds of unsteady and coupling effects of wind condition and blade structure'thus making accurate prediction of the turbine performance very difficult.Particularly'when unsteady flow field'accompanying frequent changes in both wind speed and wind direction'passes through the long and slender blades as well as through the tall tower'it inevitably results in the so-called aero-elastic problem' i.e.the interaction between aerodynamic forces and rotor motion.Therefore'it is necessary to develop accurate coupled methods between the aerodynamic model with structure model in wind turbine design to enable vibration alleviation and to develop control strategy.
Among the different aerodynamic theories to model the rotor aerodynamics[1-3]'the vortex theory is considered as one of the most suitable approximations because of its affordable computational costs and reasonably accurate results.In addition'vortex models are made up of a blade aerodynamic model including lifting line'lifting surface or panel method[4]to describe the flow around the blade'as well as to calculate the trailed and shed vorticitis released to the wake' using prescribed[5-7]or free wake[8-11]models to describe the wake geometry.The free wake models are more suitable for general rotor configurations'since the wake is allowed to freely distortunder the influence of the local velocity field.In the present work'the free wake model consists of near vortex sheets and far wake tip vertical filaments.Eor aero-elastic simulations'the free wake model is complemented with an elastic rotor model for the rotor dynamics[12-14].The modal superposition method is used to solve the wind turbine elastic problem in this paper.
1 Aerodynamic Model
It is assumed that the flow field is incompressible and potential in the free vortex wake(EVW)model for the wind turbine.The blade is modeled as a series of elements'which are represented as a line of bound vorticity lying along the blade quarter chord line.The vertical filaments'
extending downstream from the trailing edge of the blade element boundary'are allowed to freely distort under the influence of local velocity field. The governing equation of the vertical filaments can be written in the form of a partial differential equation as
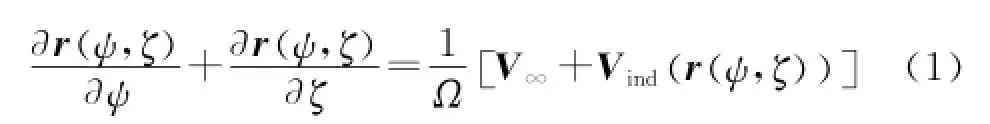
where the blade azimuth angleψis a temporal coordinate and the wake age angleζis a spatial coordinate.On the right hand side of Eq.(1)'Vindequals to the mean value of the induced velocities at the surrounding four grid points calculated by the Eiot-Savart law.To solve the partial differential equation numerically'the finite difference approximations are used to approximate the derivatives on the left hand side.Eor the spatial(ζ)derivative'a five-point central difference approximation has been used based on the predictor-corrector central(PCC)difference[15]and the predictor-corrector second backward(PC2E)[16].The accuracy of the temporal(ψ)derivative approximation plays a significant role in the time-accurate free vortex method.The PC2E algorithm uses a second-order backward difference approximation'whereas the PCC algorithm still uses a five-point central difference approximation.
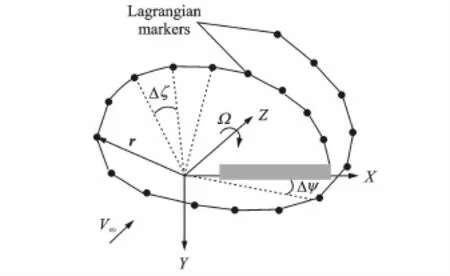
Eig.1 Schematic of discretized tip vortex geometry
In the present work'a new time-accurate algorithm is developed for overall convergence in the numerical iterations.Eor this'Eq.(1)can be written in another form as
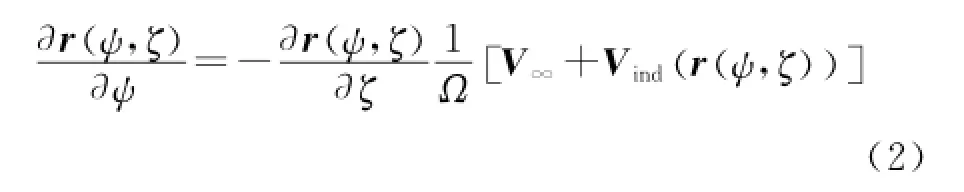
Eq.(2)can be written in a general form of ordinary derivative equation as
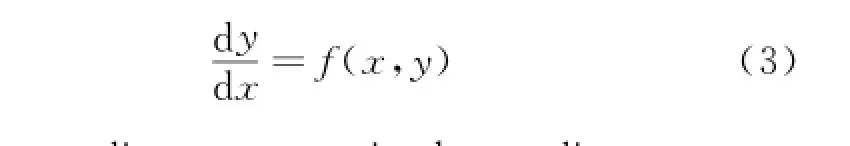
The predictor process in the predictor-corrector algorithm adopts an explicit format'whereas the corrector process adopts an implicit format. Assuming the steps are equal'the general form of the linear multistep method for Eq.(3)is written as
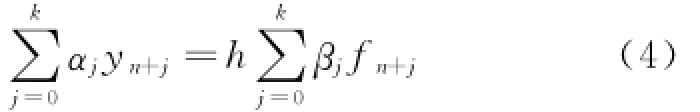
where yn+jand fn+jrepresent the terms of y(xn+j)and f(xn+j'yn+j)'respectively.The values of constantsαjandβj(j=0'1…'k)can be obtained using the method of undetermined coefficients.An explicit three-step linear multistep method is given by

The local truncation error of Eq.(5)is
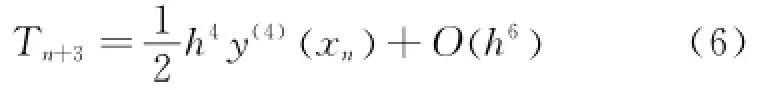
An implicit three-step linear multistep method is given by
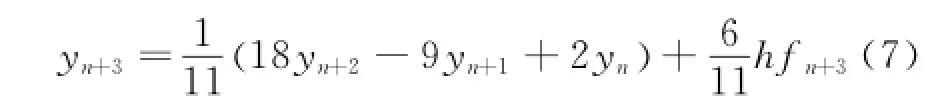
The local truncation error of Eq.(7)is

The explicit and implicit three-step linear multistep methods are used in the temporal(ψ)derivative approximation.A new predictorcorrector algorithm is developed as
Eor the predictor
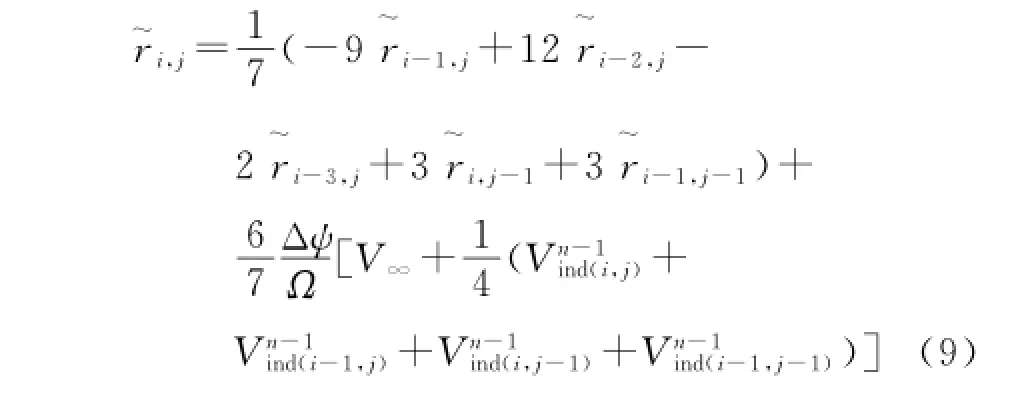
and for the corrector

It is obvious from the local truncation errors of Eqs.(5'7)that the new predictor-corrector algorithm has third-order accuracy'and therefore this algorithm is referred as the three-step and third-order predictor-corrector(D3PC)algorithm.PCC is a single-step algorithm and has second-order accuracy.The single-step algorithm is simple'but its numerical stability is not good enough.The multistep method has recently been widely used since it has better stability and convergence.Although the PC3E algorithm is a three-step algorithm'it only achieves secondorder accuracy'which results in low efficiency. The D3PC algorithm developed in this paper is also a three-step algorithm'but is of third-order accuracy.
In this paper'the three-dimensional rotational model is included in the aerodynamic model. The three-dimensional rotational effect is one of the typical differences between rotor and fixed wing'which is characterised by significantly increased lift coefficient compared with the corresponding 2D case.The higher anales of attack can contribute to the delay of the occurrence of flow separation.Du-Selig stall-delay model[17]0 coupled with the free vortex wake model is used to modify the airfoil aerodynamic data by consideration of the three-dimensional rotational effect here.
The aerodynamic loading is caused by the flow past the wind turbine structure composed of the blades and the tower.The air loads can be calculated through the discrete blade element method.Every blade element is regarded as a 2-D airfoil'and the relative velocity vector Vrelis obtained from
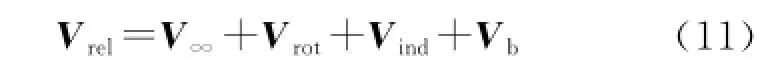
2 Dynamics Equation for Aerodynamic and Structural CouPling
If a wind turbine is described as a discretized mechanical system'the principle work is to correctly set up the mass matrix M'stiffness matrix K'and damping matrix C'for the dynamics equation
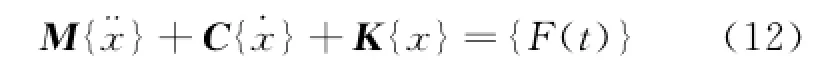
where{F(t)}denotes the generalized force vector associated with the external loads.x is the generalized displacement.In this paper'the Newmark method is used to solve the dynamics equation. The discretized calculation process to solve the dynamics equation is presented aswhere the subscript represents the time-step number.The displacements at the time step n+1 are calculated from the results of the previous time step n'at which the displacements'velocities'and accelerations for each node are already known.

The generalized displacement and velocity in the form of expansion from the time step n to the time step n+1 are given by
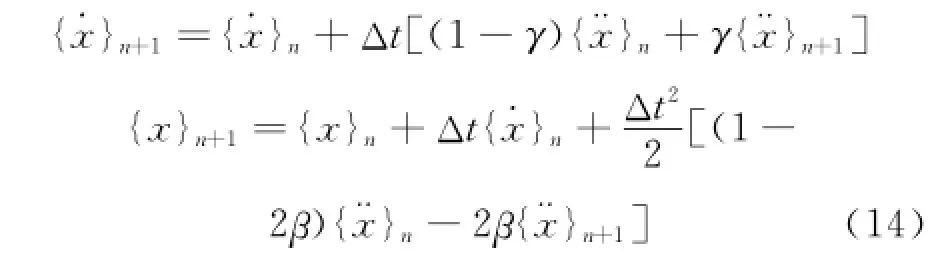
whereγ=0.5 andβ=0.25 are the trapezoidal conditions in order to guarantee unconditional convergence.It is worthy to note that a small enough computing time step is required for gaining more accurate structural dynamic response. Here'the time step is chosen on the basis of the one tenth of the rotating cycle when the structural response is significant enough.The calculation procedure is shown in Eig.2.(EVW:the free vortex wake method'EEM:the finite element modeling)
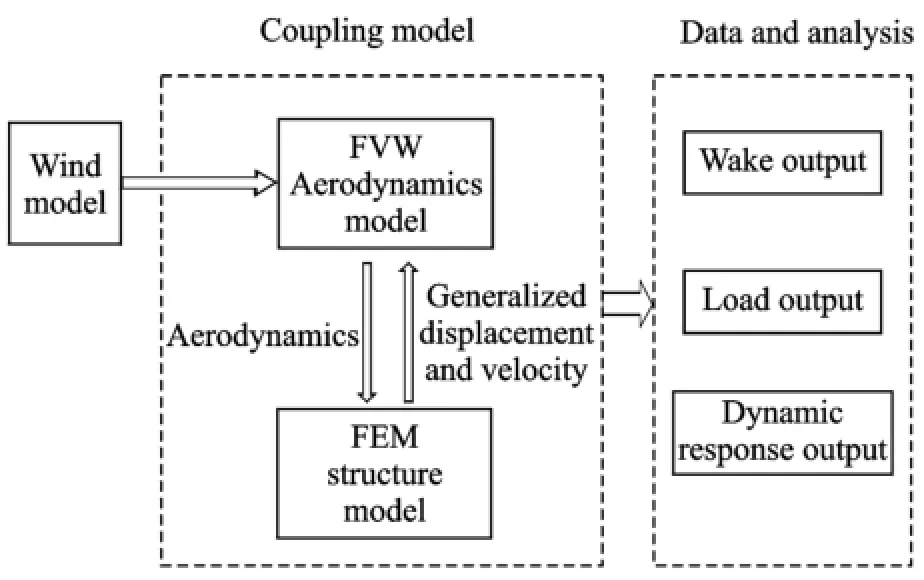
Eig.2 Calculation procedures for dynamic responses
The blade gravitational force and centrifugal force are included in the calculation.Gravity is responsible for a sinusoidal loading of the blades with a frequency corresponding to the rotation of the rotor.The blade experiences tensile stress and compressive stress because of the gravitational loads'thus resulting in the blade vibration deformation and affecting the rotor aerodynamic performance.The gravitational loading is obtained from
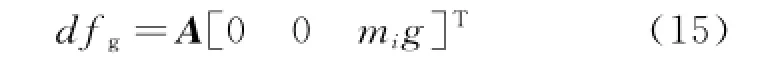
where A is the coordinate system transformation matrix'mithe i th blade element mass'and dfgthe gravitational loading of the i th blade element.
The inertial loading stems from the centrifugal force on the blades due to rotation.The centrifugal force dfcacting on the blade element at a radius r from the rotational axis is obtained by

3 Numerical Results and Analyses
3.1 Calculation model validation
对3种不同粗糙度的铝材料进行BRDF对比测试,所选粗糙度Ra分别为2.5,5,8 μm。入射角度θi分别为0°和30°,实验测量的BRDF,如图7所示。
The National Renewable Energy Laboratory(NREL)Phase VI rotor geometry'aerodynamic and structural properties are well documented in Ref.[18].The operating condition for the experiment is varied from wind speed of 7 to 25 m/s. The rotor speed is 72 r/min with the cone angle of tip pitch being 3°and 0°.The rotor radius is 5.029 m.
Eig.3 shows the variation of rotor torque with wind speed'and comparison with the experiment data.The calculation results agree well with the experimental data at low wind speeds. At higher wind speeds'however'there are discrepancies'probably due to the stall effects.
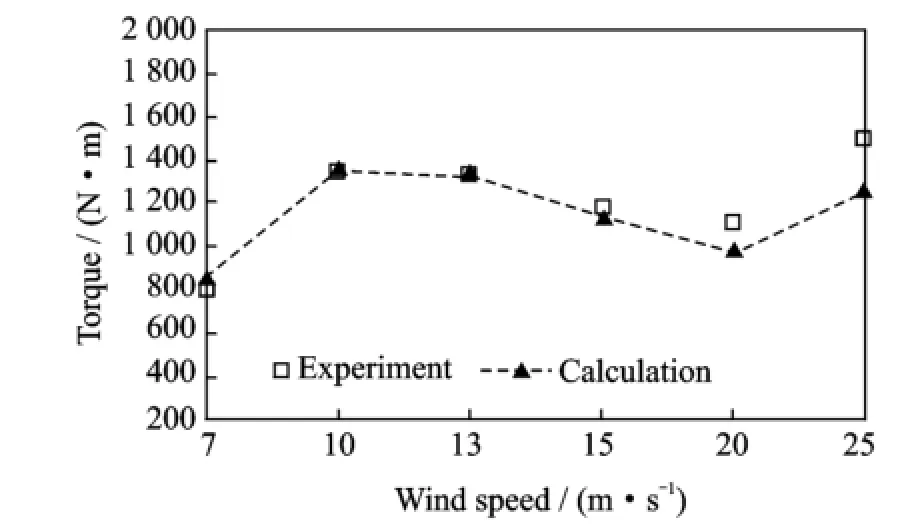
Eig.3 Variation of rotor torque with wind speed
Eig.4 shows the variation of normal and tangential coefficients at different span with wind speed.Ranging from low to high wind speeds'it is found that the normal and tangential force coef-ficients of the blade root are slightly worse than other part of the blade'which is due to the fact that the blade root suffers the serious stall effect. It is difficult to simulate the stall situation.The better stall model is needed to use in the free wake method.However'both the middle and tip part of blade have a good match with the experimental data.Therefore'one can say that the calculation model is well used to calculation the loads of the wind turbine.

Eig.4 Variation of normal and tangential coefficients at different wind speeds
3.2 Large-scale wind turbine numerical results and analyses
The NH1500 wind turbine is adopted as a calculation example in this paper.The calculation time step is 10°/Ω.The wind speed is 8 m/s.To reflect the similarity of NH1500 and real 1.5 MW wind turbine'the rotor main parameters are shown in Table 1.It can be seem that the rated power of NH1500 is 1.5 MW.The NH1500 and real 1.5 MW wind turbine have the similar blade length and wind speed operational condition.And the NH1500 also adopts the variable-pitch variable speed control strategy.Moreover'to describe the NH1500 detailedly'the NH1500 blade main structural parameters are shown in Table 2.All the aerodynamic centers of blade are located in a quarter chord length.Mass and elastic centers are given through chord length percentage in the airfoil coordinates.

Table 1 NH1500 rotor Parameters
Here'the finite element method is applied to establish the wind turbine structural model. Two-node beams and shell elements are used to model the blade and tower'respectively.The nacelle mass and moment of inertia are simulated through the 0D element in PATRAN software. The rotor is rigidly connected to the tower.The boundary conditions are imposed at the bottom of the tower through fixed constraints.The modes of NH1500 wind turbine are calculated at the rotational speed of 17.2 r/min with the calculatedmodes shown in Table 3.
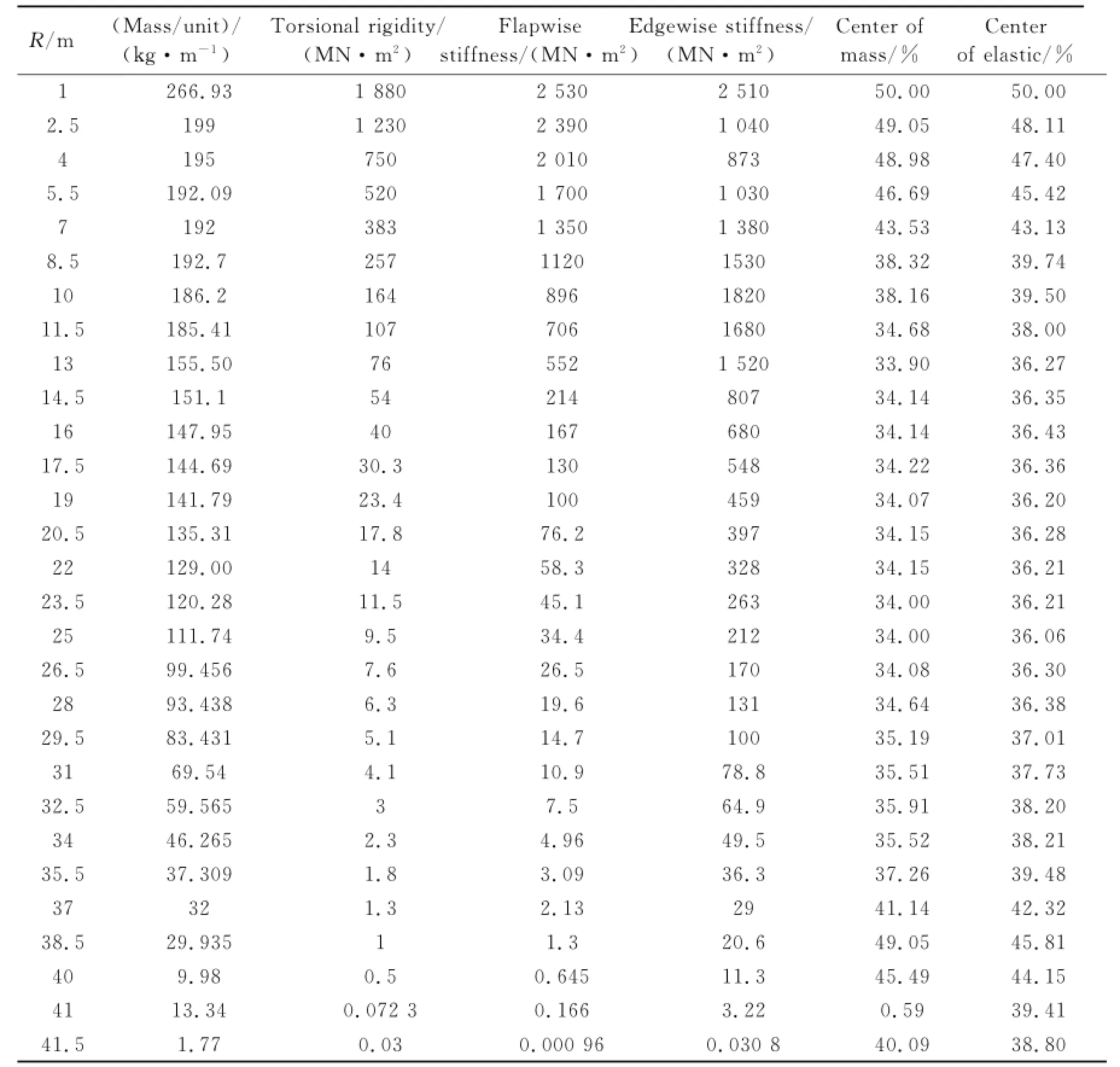
Table 2 Main structural Parameters for the NH1500 blade
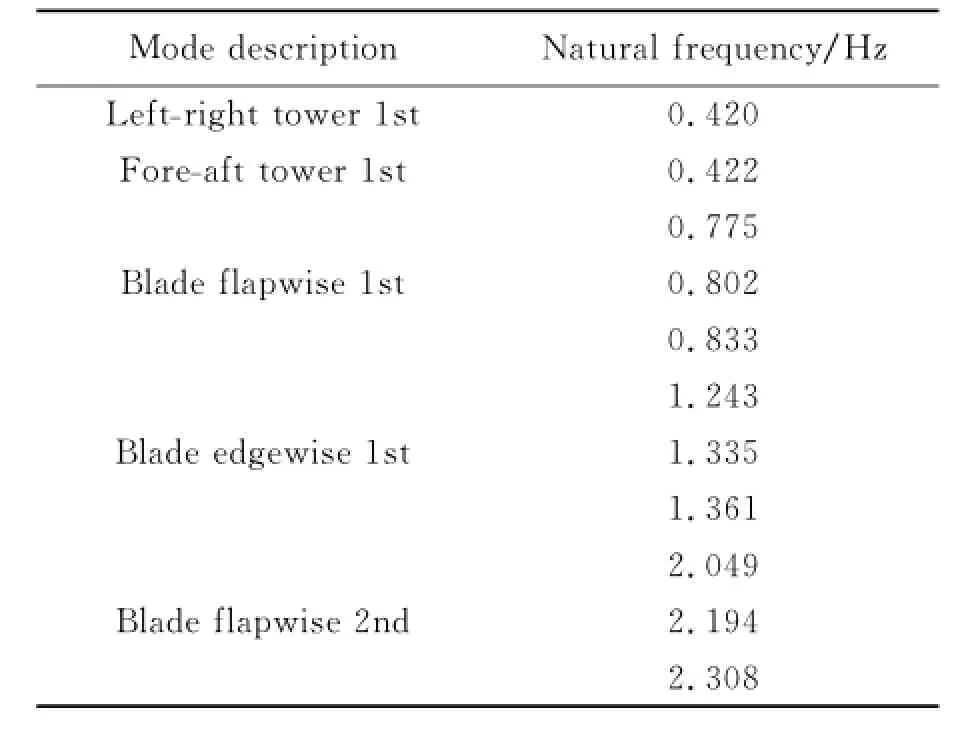
Table 3 Mode descriPtion
Eig.5 shows the comparison of calculated value and experimental value.NH1500 is a 1/16 scaled model on the experiment.The calculated data and experimental data changing trend are basically consistent.In Eig.5'the calculation values are slightly higher than the experiment data. The probable reason is that the experiment wind turbine model is a scaled model.
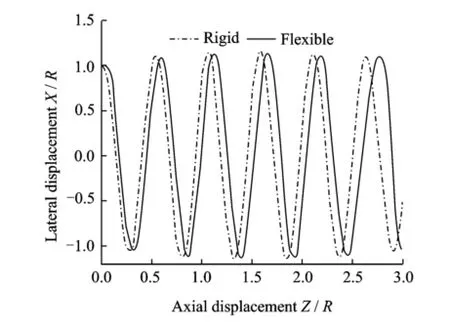
Eig.6 shows the downstream displacements of the blade tip vortex'calculated from the EVW method.To investigate the blade deformation effect'the NH1500 blade is considered rigid and flexible'respectively.It can be clearly seen from Eig.6 that the difference in the vortex position between the assumed rigid blade and the actual flexible blade.The displacement difference increases from 0.05R to 0.1R as the tip vortex fila-ment moves downstream.It can be reasoned that this difference has influence on the air load calculation through the induced velocity calculation' which depends on the spatial distance of the vortex to the blade.
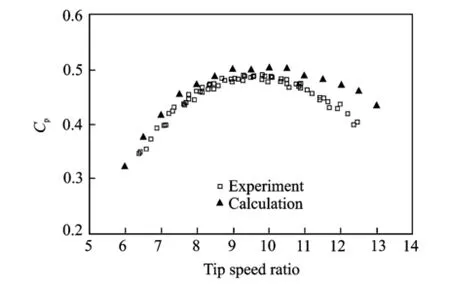
Eig.5 Cpof NH1500
Eor further analysis'the wind speed distribution and the vorticity of the wake are calculated.The wind speed of the wake V(Vx'Vy'Vz)is defined as
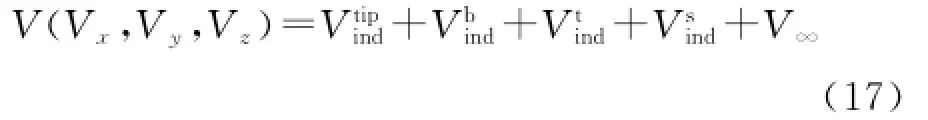
To find the wind speed of the wake seen by V(Vx'Vy'Vz)'the induced velocity of the tip vortex'the induced velocity of the bound vortex'the induced velocity of the trailed vortex'and the induced velocity of the shed vortex'must be added as vectors into the inflow velocity'V∞.
As the wind speed distribution is known'the vorticityis calculated by
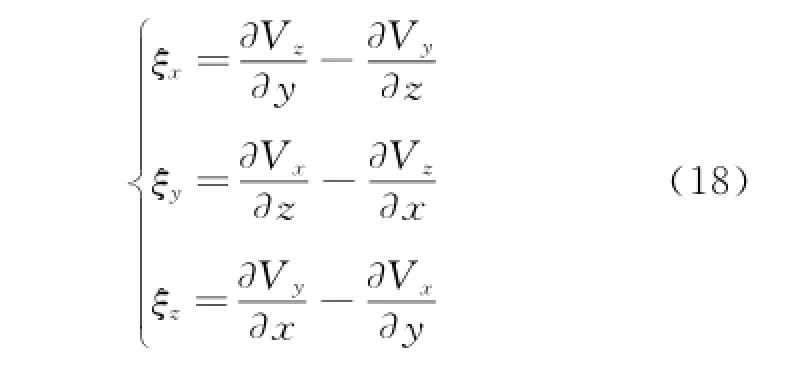
Eigs.7'8 give the development and evolvement of the tip vortex for the rigid and flexible blades with the axial downstream distance'respectively.The vortical strength increases downstream just behind the rotor with a wake expansion'but gradually dissipates as the axial distance further increases for the both cases.However' both the vortical strength and the wake expansion for the assumed rigid rotor are stronger than those for the actual flexible rotor.
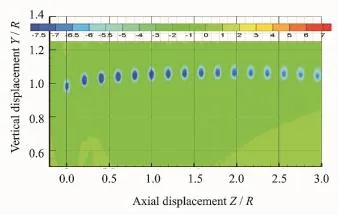
Eig.7 Axial distribution of tip vortex for rigid blade
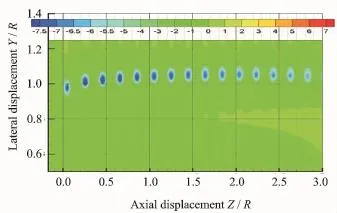
Eig.8 Axial distribution of tip vortex for flexible blade
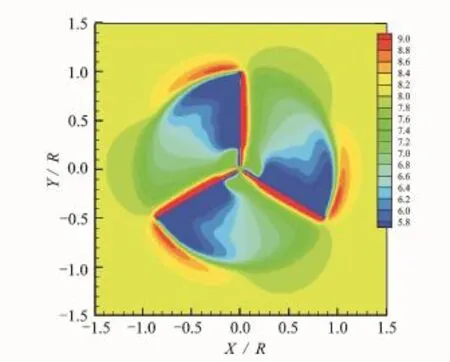
Eig.9 0R section distribution of wind speed Vz(m/s)of rigid blade
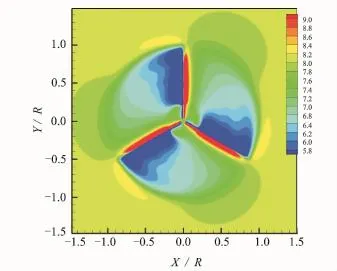
Eig.10 0R section distribution of wind speed Vz(m/s)of flexible blade
Eig.9 shows the 0R section distribution of the wind speed of the rigid blade.Eig.10 shows the 0R section distribution of the wind speed of the flexible blade.It is found that the 0R section wind speeds of the flexible blade are weaker than the rigid due to the structural deformation.The effect is significant for wake prediction.
Eig.11 illustrates some representative numerical results among which the aerodynamic characteristics are presented by the blade root loads for the flexible case at the wind speed of 8 m/s.The root loads all fluctuate sinusoidally with azimuthally angle for both cases with and without gravity considered.Nevertheless'the amplitudes of the load variation differ from each other due to the gravitational effect.In addition' the blade dynamic deformation is also influenced by the gravity.The dynamic displacement in the flapwise direction when gravitational force is not considered is only about 4%of that when the gravitational force is taken into account'as shown in Eig.12.
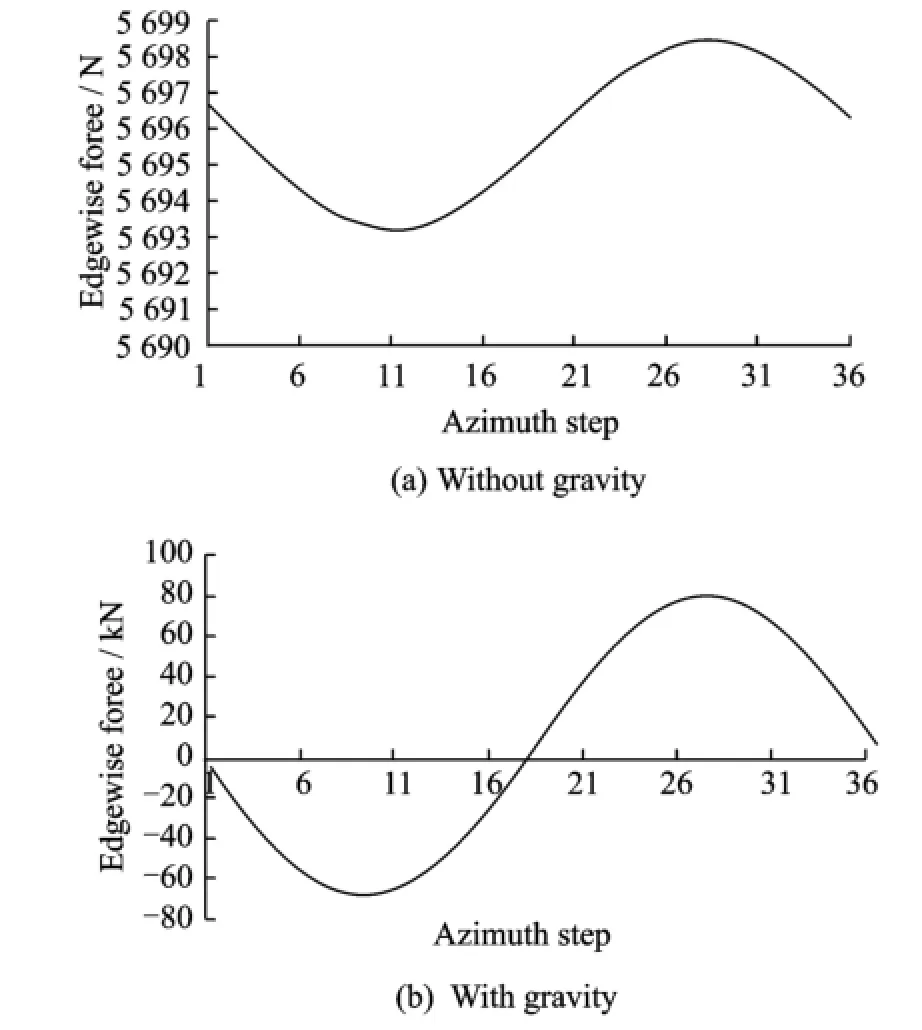
Eig.11 Edgewise force at blade root
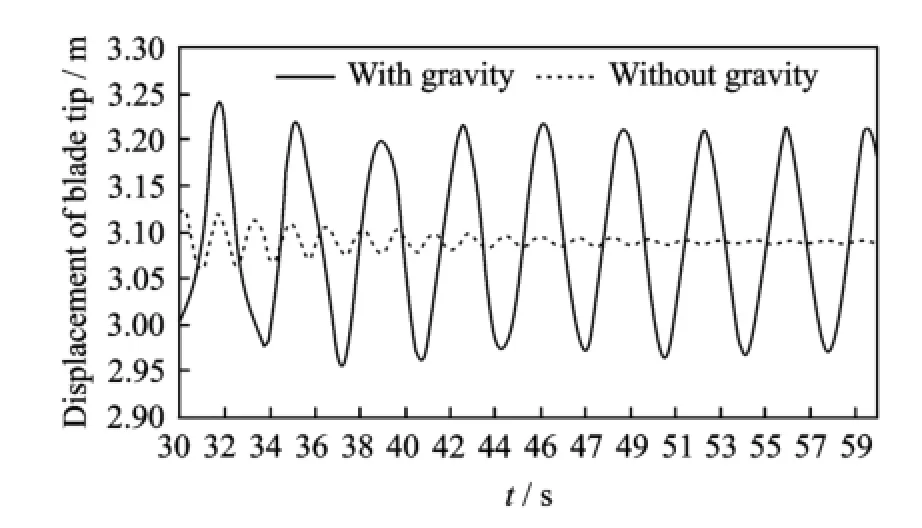
Eig.12 Dynamic displacements at blade tip in flapwise direction

Eig.13 Wind turbine power coefficients'V∞=8 m/s
It is obvious from Eig.13'where the windturbine power coefficient Cpis compared between the rigid and flexible considerations'that the flexible wind turbine Cpis larger than the rigid one and changes with azimuth angle.According to the comparison of minimum value'the flexible wind turbine Cpis 1.6%more than the rigid one. It is the reason that the flapwise direction induced velocity of flexible blade has a larger change amplitude than the edgewise direction induced velocity.And the flapwise direction induced velocity is weaker than the rigid one.Thus'the attack angle and the flow angle of flexible blade are both larger.Einally'the tangential force coefficient to the rotor is larger'which can lead to the increasing of torque and Cp.
4 Conclusions
The numerical analysis of wind turbine wake and loads are presented in this paper.An aerodynamically and structurally coupled model is developed and used to predict the flexible wind turbine loads and aerodynamic performance.The results demonstrate that EVW and EEM coupling model can predict the wind turbine dynamic characteristics effectively and efficiently.The dynamic displacement in the flapwise direction without considering gravitational force is only 4%of that with gravitational force.Moreover'according to the comparison of minimum value of Cp'the Cpvalue of the flexible wind turbine is 1.6%more than that of the rigid one.Despite the fact that the accuracy of the calculated results needs to be improved for further validation by experiment data'the wind turbine wake and dynamic response can be better understood through the results obtained from this study.
Acknowledgements
This work was supported by the National Easic Research Program of China(973 Program)(No. 2014CE046200)'the Jiangsu Province Natural Science Eoundation(No.EK2012390)'the Eundamental Research Eunds for the Central Universities'and the Priority Academic Program Development of Jiangsu Higher Education Institutions.
[1] Ghadirian A'Dehghan M'Torabi E.Considering induction factor using EEM method in wind farm layout optimization[J].Journal of Wind Engineering and Industrial Aerodynamics'2014'129:31-39.
[2] Zhang Zhenyu'Zhou Hanwei'Wang Tongguang. Numerical analysis of influence of Gurney flaps applied to wind turbines[J].Transactions of Nanjing University of Aeronautics&Astronautics'2014'31(5):576-579.
[3] Hsu MingChen'Akkerman I'Eazilevs Y.Einite element simulation of wind turbine aerodynamics:Validation study using NREL Phase VI experiment[J]. Wind Energy'2014'17:461-481.
[4] Grasso E'van Garrel A'Schepers G.Development and validation of generalized lifting line based code for wind turbine aerodynamics[C]∥The 30th ASME wind energy symposium'Elorida'USA:[s.n.]' 2011:146-152.
[5] Scheurich E'Eletcher T M'Erown R E.Simulating the aerodynamic performance and wake dynamics of a vertical-axis wind turbine[J].Wind Energy'2011'14(2):159-177.
[6] Ereton S P'Coton E N'Moe G.A study on rotational effects and different stall delay models using a prescribed wake vortex scheme and NREL phase VI experiment data[J].Wind Energy'2008'11:459-482.
[7] Wang T G.Unsteady aerodynamic modelling of horizontal axis wind turbine performance[D].Scotland' UK:University of Glasgow'1999.
[8] Sebastian T'Lackner MA.Development of a free vortex wake method code for offshore floating wind turbines[J].Renewable Energy'2012'46:269-275.
[9] Zhou W P'Tang S L'LüH.Computation on aerodynamic performance of horizontal axis wind turbine based on time-marching free vortex method[J].Chin Soc for Elec Eng'2011'31(29):124-130.
[10]Jeon M'Lee S.Unsteady aerodynamics of offshore floating wind turbines in platform pitching motion using vortex lattice method[J].Renewable Energy' 2014'65:207-212.
[11]Gupta S'Leishman J G.Performance pre-dictions of the NREL phaseⅥcombined Ex-periment rotor using a free-vortex wake model[C]∥Collection ofTechnical Papers—44th AIAA Aerospace Sciences Meeting.[S.l.]:AIAA'2006:4544-4564.
[12]Eelco H'Gustaaf J'Asfaw E.Aero-elastic behavior of a flexible blade for wind turbine application:A 2D computational study[J].Energy'2010'35:778-785.
[13]Ahlstrom A.Aeroelastic simulation of wind turbine dynamics[D].Sweden:Royal Institute of Technology Department of Mechanics'2005.
[14]Ng E E'Hesse H'Palacios R.Aeroservoelastic state space vortex lattice modeling and load alleviation of wind turbine blades[J].Wind Energy'2014' 17(4):DOI:10.1002/we.1752.
[15]Ehagwat M J'Leishman J G.Rotor aerodynamics during maneuvering flight usinga time-accurate freevortex wake[J].Journal of the American Helicopter Society'2003'48:143-158.
[16]Ehagwat M J'Leishman J G.Time-accurate free vortex wake model for dynamic rotor response[C]∥American Helicopter Society Specialist Meeting.Atlanta'USA:[s.n.]'2000.
[17]Du Z'Selig M S.A 3-D stall-delay model for horizontal axis wind turbine performance prediction[R]. AIAA-98-0021'1998.
[18]Hand M'Simms D A.Unsteady aerodynamicexperiment phase VI:Wind tunnel test configurations and available data campaigns[R].National Renewable Energy Laboratory.Colorado:National Technical Information Service'2001.
(Executive editor:Xu Chengting)
O35 Document code:A Article ID:1005-1120(2015)02-0240-10
*CorresPonding author:Wang Tongguang'Professor'E-mail:tgwang@nuaa.edu.cn.
How to cite this article:Cao Jiufa'Wang Tongguang'Long Hui'et al.Dynamic loads and wake prediction for large wind turbines based on free wake method[J].Trans.Nanjing U.Aero.Astro.'2015'32(2):240-249.
http://dx.doi.org/10.16356/j.1005-1120.2015.02.240
(Received 13 November 2014;revised 7 January 2015;accepted 12 January 2015)
猜你喜欢
杂志排行
Transactions of Nanjing University of Aeronautics and Astronautics的其它文章
- Numerical Investigation on Drag Reduction Effect by Mass Injection from Porous Boundary Wall
- Posture Adjustment of MicroPhone Based on Image Recognition in Automatic Welding System
- StePPing Control Method of Linear DisPlacement Mechanism Driven by TRUM Based on PSoC
- Dynamic Model Identification for Ultrasonic Motor Frequency-SPeed Control
- Intelligent Control Algorithm of PTZ System Driven by Two-DOF Ultrasonic Motor
- Large Thrust Trans-scale Precision Positioning Stage Based on Inertial Stick-SliP Driving
