板厚与波高对波纹钢管涵受力性能影响分析

唐 杨，王国炜，安 海，亓兴军

(1.五峰土家族自治县农村公路管理所，湖北 宜昌 443413；2.济南金衢公路勘察设计研究有限公司，山东 济南 250101；3.国网西藏电力有限公司昌都供电公司，西藏 昌都 854000；4.山东建筑大学 交通工程学院，山东 济南 250101)

波纹钢管涵具有抗变形能力强、施工时间短、造价低廉、建材环保等优点[1]，在特殊岩土地质区、交通不便的山区、冻融循环显著的高寒地区得到了广泛的应用[2-3]，同时在桥涵加固[4-5]和应急抢修[6]中表现突出。

通过查阅相关文献发现，波纹钢管涵的研究主要集中在特殊岩土地质区的应用[7]、力学性能的测试[8]、有限元仿真分析[9-12]和施工工艺优化[13]等几个方面，而对波纹钢板的结构参数对波纹钢管涵受力性能的影响研究较少。

根据相关规范建立波纹钢管涵的有限元模型，考虑到波纹钢独特的力学特性[14-16]，通过改变波纹钢板的结构参数建立多个对比模型，研究其结构参数对波纹钢管涵受力性能的影响。

1 分析思路

1.1 分析模型

根据《公路桥涵用波形钢板》(JT/T 710—2008)[17]，选用其中的F波型建立波纹钢板的几何模型，F波型的波距为400 mm，波深为180 mm(波高为90 mm)，半径为90 mm，板厚为6 mm。波纹钢管涵的有限元模型采用Midas FEA建立。波纹钢管涵的几何模型包含2.5个波形，结构尺寸如图1所示，将波形旋转即可得到波纹钢管涵的几何模型，旋转半径为0.5 m，得到的波纹钢管涵的跨度为1 m。

图1 波形钢板结构尺寸(单位：mm)

钢板的本构模型设置为弹性模型，弹性模量为210 GPa，容重为78.5 kN/m3，泊松比为0.3。土体的本构模型设置为摩尔-库伦模型，弹性模量为81 MPa，容重为19.3 kN/m3，泊松比为0.25，黏聚力为118 kPa，摩擦角为22°，剪膨胀角为0°。

根据圣维南原理，取一定土体范围进行建模，即波纹钢管涵四周的土体至少为一倍管径的厚度[8]，故而将波纹钢管涵四周的土体取1.5 m，波纹钢管涵的管轴方向取1.0 m。几何模型完成后分别划分土体和波纹钢管涵的有限元网格，将土体和波纹钢管相切面的节点共节点处理[9]。为了降低计算量，根据对称性条件仅仅对一半结构建立有限元模型。波纹钢管涵的有限元模型如图2所示。除了对称边界条件以外，将土体的底部固结，两侧限制水平位移。在荷载上考虑自重和汽车荷载。汽车荷载采用面压力施加于管涵上部土体的表面，参考《公路桥涵通用设计规范》(JTG D60—2015)[18]中关于车辆荷载的取值，接触面积设置为0.6 m×0.8 m，压力总量设置为120 kN。分析工况设置为非线性静力分析，计算方法采用Newton Rapson迭代法，荷载步骤数设置为5，最大迭代步骤数设置为100。

图2 波纹钢管涵有限元模型

1.2 分析方法

为了更好地表述分析结果，将波纹钢管涵的不同位置指定名称。结构位移的提取截面为波峰截面(管轴方向中间截面)和波谷截面(距离管轴方向中间截面最近的波谷截面)，如图1所示。每个截面提取9个点的数据，包括2个端点(顶点、最低点)和由顶点逆时针旋转到最低点之间的7个中间点，依次为1/8点、1/4点、3/8点、1/2点、5/8点、3/4点、7/8点，每个点之间的弧长长度相等，各点位置如图3所示。

图3 节点位置图

波纹钢管涵的受力影响因素主要考虑板厚和波高2方面，在具体分析中通过改变板厚和波高的结构参数从变形和应力2方面进行对比分析。在变形分析上，通过波纹钢管涵波峰截面和波谷截面的位移分析结果计算得到变形分析结果，具体计算方法为：以1/2点的水平位移乘以-2得到波纹钢管涵的水平变形，以顶点的竖向位移减去最低点的竖向位移得到波纹钢管涵的竖向变形。在应力分析上，通过提取波峰截面和波谷截面的各节点Mises应力进行对比分析。

2 板厚的影响分析

将上面的计算模型修改板厚参数，即将板厚6 mm重新设置为2、3、4、5 mm，用于分析板厚对波纹钢管涵受力性能的影响。

2.1 变形分析

通过计算，得到波纹钢管涵在不同板厚条件下的位移云图，提取波纹钢管涵波峰截面和波谷截面各节点的水平位移如图4所示，竖向位移如图5所示，计算得到水平变形和竖向变形如图6所示。

图4 波纹钢管涵在不同板厚条件下的水平位移

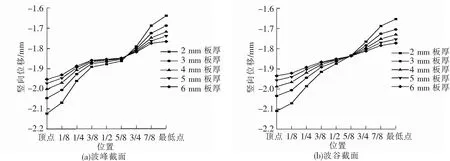
图5 波纹钢管涵在不同板厚条件下的竖向位移

图6 波纹钢管涵在不同板厚条件下的结构变形

由图4(a)可以看出，波峰截面的水平位移先后3次呈现先增大后减小的变化趋势，波峰截面在1/2点时的水平位移达到最大值。随着板厚的减小，波纹钢管涵在波峰截面的水平位移越来越大，且水平位移的增长幅度越来越大。当板厚为6 mm时，波峰截面在1/2点的水平位移为0.047 mm；当板厚为5 mm时，波峰截面在1/2点的水平位移为0.057 mm，相比于板厚为6 mm时增大21.28%；当板厚为4 mm时，波峰截面在1/2点的水平位移为0.071 mm，相比于板厚为6 mm时增大51.06%；当板厚为3 mm时，波峰截面在1/2点的水平位移为0.092 mm，相比于板厚为6 mm时增大95.74%；当板厚为2 mm时，波峰截面在1/2点的水平位移为0.127 mm，水平位移增大到板厚为6 mm时的2.70倍。由此可见，随着波纹钢板板厚的减小，波纹钢管涵在波峰截面的刚度下降越来越快。

由图4(b)可以看出，波谷截面的水平位移仅仅呈现一次先增大后减小的变化过程，在1/2点时波谷截面的水平位移达到最大值。当板厚为6 mm时，波谷截面在1/2点的水平位移为0.084 mm；当板厚为5 mm时，波谷截面在1/2点的水平位移为0.101 mm，相比于板厚为6 mm时增大20.24%；当板厚为4 mm时，波谷截面在1/2点的水平位移为0.125 mm，相比于板厚为6 mm时增大48.81%；当板厚为3 mm时，波谷截面在1/2点的水平位移为0.158 mm，相比于板厚为6 mm时增大88.10%；当板厚为2 mm时，波谷截面在1/2点的水平位移为0.206 mm，水平位移增大到板厚为6 mm时的2.45倍。由此可知，随着板厚的减小，波纹钢管涵在波谷截面的水平位移越来越大，且水平位移的增长幅度越来越大，波谷截面的刚度下降速度亦越来越快。

由图5(a)可以看出，波峰截面的竖向位移呈现逐渐增大的变化趋势，在顶点存在竖向位移最大值，在最低点存在竖向位移最小值。当板厚为6 mm时，波峰截面在顶点的竖向位移为1.955 mm；当板厚为5 mm时，波峰截面在顶点的竖向位移为1.975 mm，相比于板厚为6 mm时增大1.02%；当板厚为4 mm时，波峰截面在顶点的竖向位移为2.004 mm，相比于板厚为6 mm时增大2.51%；当板厚为3 mm时，波峰截面在顶点的竖向位移为2.049 mm，相比于板厚为6 mm时增大4.81%；当板厚为2 mm时，波峰截面在顶点的竖向位移为2.125 mm，相比于板厚为6 mm时增大8.70%。由此可见，随着板厚的减小，波纹钢管涵在波峰截面的竖向位移越来越大，且竖向位移的增长幅度越来越大。

由图5(b)可以看出，波谷截面的竖向位移同样呈现逐渐增大的变化趋势。随着板厚的减小，波纹钢管涵在波谷截面的竖向位移越来越大，在顶点达到最大值，在最低点达到最小值。当板厚为6 mm时，波谷截面在顶点的竖向位移为1.938 mm；当板厚为5 mm时，波谷截面在顶点的竖向位移为1.960 mm，相比于板厚为6 mm时增大1.14%；当板厚为4 mm时，波谷截面在顶点的竖向位移为1.991 mm，相比于板厚为6 mm时增大2.73%；当板厚为3 mm时，波谷截面在顶点的竖向位移为2.049 mm，相比于板厚为6 mm时增大5.73%；当板厚为2 mm时，波谷截面在顶点的竖向位移为2.112 mm，相比于板厚为6 mm时增大8.98%。由此可见，随着板厚的减小，波纹钢管涵波峰截面的竖向位移越来越大，且竖向位移的增长幅度越来越大。

由图6可以看出，随着板厚的增大，波峰截面、波谷截面的水平变形和竖向变形越来越小。板厚由2 mm增大到6 mm，波峰截面的水平变形由0.253 mm下降到0.095 mm，波谷截面的水平变形由0.412 mm下降到0.167 mm；波峰截面的竖向变形由0.486 mm下降到0.188 mm，波谷截面的竖向变形由0.455 mm下降到0.182 mm。

2.2 应力分析

提取波峰截面和波谷截面各点在不同板厚条件下的Mises应力如图7所示。

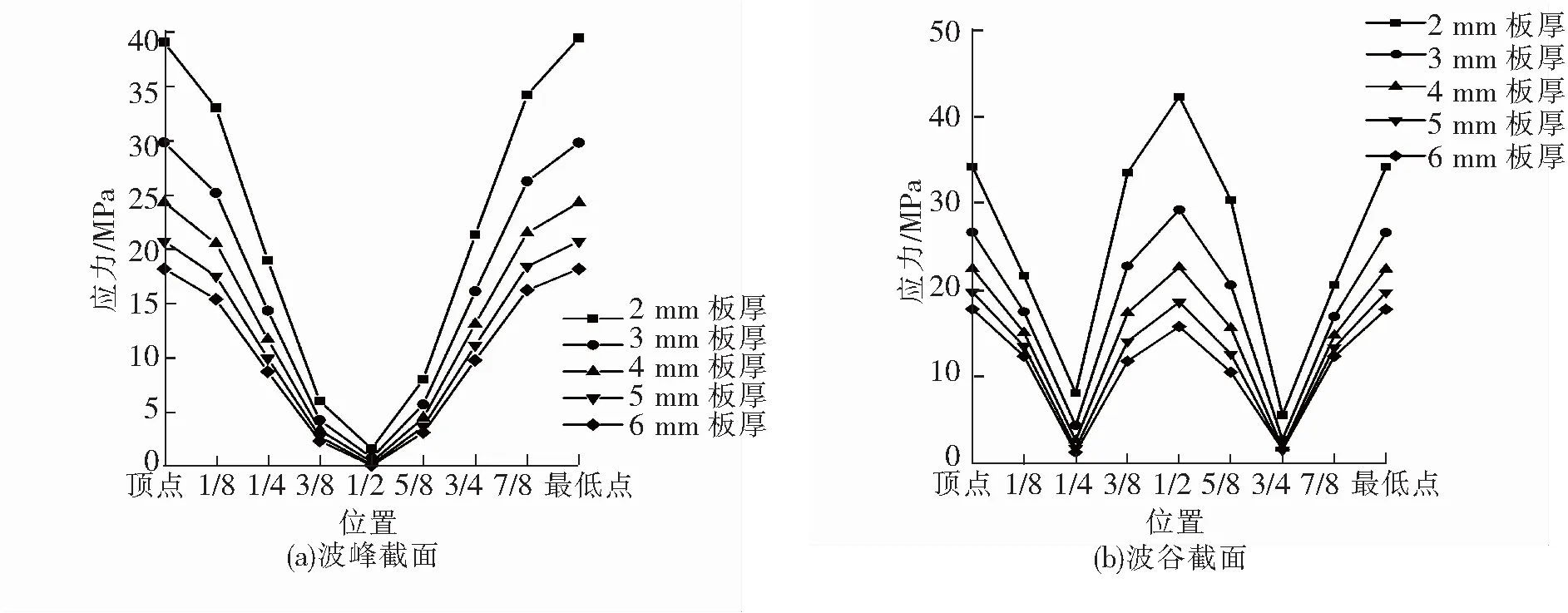
图7 波纹钢管涵在不同板厚条件下的Mises应力

由图7(a)可以看出，波峰截面的Mises应力在1/2点达到最小值，在顶点或者最低点达到最大值。随着板厚的减小，顶点和最低点的应力越来越大。当板厚为6 mm时，波峰截面的最大Mises应力为18.162 MPa；当板厚为5 mm时，波峰截面的最大Mises应力为20.692 MPa，相比于板厚为6 mm时增大13.93%；当板厚为4 mm时，波峰截面的最大Mises应力为24.278 MPa，相比于板厚为6 mm时增大33.67%；当板厚为3 mm时，波峰截面的最大Mises应力为29.783 MPa，相比于板厚为6 mm时增大63.99%；当板厚为2 mm时，波峰截面的最大Mises应力为39.427 MPa，最大应力增大到板厚为6 mm时的2.17倍。

由图7(b)可以看出，波谷截面的Mises应力关于1/2点对称，在对称一侧呈现先减小后增大的变化趋势。在1/4点达到最小值，在顶点、1/2点、最低点的应力值均较大。当板厚为6 mm时，波谷截面的最大Mises应力为17.814 MPa；当板厚为5 mm时，波谷截面的最大Mises应力为19.764 MPa，相比于板厚为6 mm时增大10.95%；当板厚为4 mm时，波谷的最大Mises应力为22.640 MPa，相比于板厚为6 mm时增大27.09%；当板厚为3 mm时，波谷截面的最大Mises应力为29.246 MPa，相比于板厚为6 mm时增大64.17%；当板厚为2 mm时，波谷的最大Mises应力为42.205 MPa，最大Mises应力增大到板厚为6 mm时的2.37倍。由此可见，板厚的下降造成波纹钢管涵更大的变形，最终导致结构Mises应力值的逐渐增大。

3 波高影响分析

波高变化时波距不变，仅仅修改波纹的圆弧段半径，各圆弧之间直线连接，直线与圆弧相切。下面将波高90 mm重新设置为50、60、70、80 mm，用于分析波高对波纹钢管涵受力性能的影响。

3.1 变形分析

通过计算，得到波纹钢管涵在不同波高下的位移，提取波纹钢管涵波峰截面、波谷截面各节点的水平位移如图8所示，竖向位移如图9所示，计算得到水平变形和竖向变形如图10所示。

图8 波纹钢管涵在不同波高条件下的水平位移

图9 波纹钢管涵在不同波高条件下的竖向位移

图10 波纹钢管涵不同波高条件下的结构变形

由图8(a)可以看出，随着波高的减小，波纹钢管涵在波峰截面的水平位移越来越大，在1/2点水平位移达到最大值，且增长幅度越来越大。当波高为90 mm时，波峰截面在1/2点的水平位移为0.047 mm；当波高为80 mm时，波峰截面在1/2点的水平位移为0.074 mm，相比于波高为90 mm时增大57.45%；当波高为70 mm时，波峰截面在1/2点的水平位移为0.120 mm，增长到波高为90 mm时的2.55倍；当波高为60 mm时，波峰截面在1/2点的水平位移为0.189 mm，增长到波高为90 mm时的4.02倍；当波高为50 mm时，波峰截面在1/2点的水平位移为0.283 mm，增长到波高为90 mm时的6.02倍。

由图8(b)可以看出，波纹钢管涵波谷截面的水平位移变化与波峰截面较为相似。当波高为90 mm时，波谷截面在1/2点的水平位移为0.084 mm；当波高为80 mm时，波谷截面在1/2点的水平位移为0.102 mm，相比于波高为90 mm时增大21.43%；当波高为70 mm时，波谷截面在1/2点的水平位移为0.147 mm，相比于波高为90 mm时增大75.00%；当波高为60 mm时，波谷截面在1/2点的水平位移为0.223 mm，增长到波高为90 mm时的2.65倍；当波高为50 mm时，波谷截面在1/2点的水平位移为0.335 mm，增长到波高为90 mm时的3.99倍。

由此可见，波纹钢板的波高与波峰截面、波谷截面的水平位移成反比，波纹钢板的波高对波纹钢管涵的位移影响较为显著。

由图9(a)可以看出，从顶点到最低点，波纹钢管涵在波峰截面的竖向位移呈减小趋势，在顶点位置存在最大竖向位移。当波高为90 mm时，波峰截面的最大竖向位移为1.955 mm；当波高为80 mm时，波峰截面的最大竖向位移为1.992 mm，相比于波高为90 mm时增大1.89%；当波高为70 mm时，波峰截面的最大竖向位移为2.050 mm，相比于波高为90 mm时增大4.86%；当波高为60 mm时，波峰截面的最大竖向位移为2.135 mm，相比于波高为90 mm时增大9.21%；当波高为50 mm时，波峰截面的最大竖向位移为2.248 mm，相比于波高为90 mm时增大14.99%。由此可见，随着波高的减小，波纹钢管涵波峰截面的竖向位移越来越大，且增长幅度越来越大。

由图9(b)可以看出，波纹钢管涵在波谷截面的竖向位移变化与波峰截面较为相似，均在顶点位置存在最大竖向位移。当波高为90 mm时，波谷截面的最大竖向位移为1.938 mm；当波高为80 mm时，波谷截面的最大竖向位移为1.963 mm，相比于波高为90 mm时增大1.29%；当波高为70 mm时，波谷截面的最大竖向位移为2.018 mm，相比于波高为90 mm时增大4.13%；当波高为60 mm时，波谷截面的最大竖向位移为2.111 mm，相比于波高为90 mm时增大8.93%；当波高为50 mm时，波谷截面的最大竖向位移为2.248 mm，相比于波高为90 mm时增大16.00%。由此可见，与波峰截面类似，波谷截面的竖向位移同样与波高成反比，且竖向位移的增长幅度相近。

由图10可以看出，随着波高的增加，波峰截面、波谷截面的水平变形和竖向变形越来越小。波高由50 mm增大到90 mm，波峰截面的水平变形由0.566 mm降低到0.095 mm，波谷截面的水平位移由0.670 mm降低到0.167 mm；波峰截面的竖向变形由0.671 mm降低到0.188 mm，波谷截面的竖向变形由0.668 mm降低到0.162 mm。由此可见，增大波纹钢板的波高可以有效提高波纹钢管涵的整体刚度。

3.2 应力分析

提取不同波高条件下波峰截面和波谷截面各点的Mises应力如图11所示。

图11 波纹钢管涵不同波高条件下的Mises应力

由图11(a)可以看出，波峰截面的Mises应力在1/2点两侧及其附近达到最小值，在顶点或最低点达到最大值。随着波高的减小，顶点和最低点的应力越来越大。当波高为90 mm时，波峰截面的最大Mises应力为18.162 MPa；当波高为80 mm时，波峰截面的最大Mises应力为21.970 MPa，相比于波高为90 mm时增大20.97%；当波高为70 mm时，波峰截面的最大Mises应力为24.961 MPa，相比于波高为90 mm时增大37.44%；当波高为60 mm时，波峰截面的最大Mises应力为29.069 MPa，相比于波高为90 mm时增大60.05%；当波高为50 mm时，波峰截面的最大Mises应力为31.250 MPa，相比于波高为90 mm时增大72.06%。

由图11(b)可以看出，波谷截面的Mises应力关于1/2点对称，在对称一侧呈现先减小后增大的变化趋势。在1/4点达到最小值，在顶点、1/2点、最低点应力值较大。当波高为90 mm时，波谷截面的最大Mises应力为17.814 MPa；当波高为80 mm时，波谷截面的最大Mises应力为25.228 MPa，相比于波高为90 mm时增大41.62%；当波高为70 mm时，波谷截面的最大Mises应力为32.341 MPa，相比于波高为90 mm增大81.55%；当波高为60 mm时，波谷截面的最大Mises应力为38.227 MPa，增大到波高为90 mm时的2.15倍；当波高为50 mm时，波谷截面的最大Mises应力为39.596 MPa，增大到波高为90 mm时的2.22倍。

综合以上计算结果来看，波纹钢管涵波峰、波谷截面的Mises应力与波纹钢板的波高成反比，增加波纹钢板的波高可以有效降低波纹钢管涵的Mises应力。

4 结论

综合以上研究，得出以下结论：

(1)波纹钢管涵的水平位移最大值出现在1/2点，由顶点到最低点，波峰截面的水平位移先后3次呈现先增大后减小的变化趋势，波谷截面的水平位移仅仅呈现一次先增大后减小的变化过程；竖向位移的最大值出现在顶点，竖向位移由顶点到最低点呈现逐渐减小的变化趋势；随着波纹钢板厚度的减小，波纹钢管涵的结构变形逐渐增大，且增长速度越来越快；波高对波纹钢管涵的变形影响与板厚相似。

(2)波纹钢管涵在波峰截面的Mises应力最小值出现在1/2点及其附近位置，在顶点或者最低点出现较大值，且顶点和最低点位置的应力值较为接近；波纹钢管涵在波谷截面的Mises应力较小值出现在1/4点或者3/4点，较大值出现在顶点、最低点和1/2点；随着波纹钢板厚度、波高的减小，波纹钢管涵的Mises应力增大。