考虑里程计截断误差的SINS/OD组合导航算法

周召发，赵芝谦，张志利，曾 进

（1. 火箭军工程大学 导弹工程学院，西安 710025；2. 航空工业自控所 惯性技术航空科技重点实验室，西安 710065）

捷联惯导系统（SINS）能够实时提供载体的姿态、速度和位置，具有全天候、自主、隐蔽等优点，已成为陆地车辆上必不可少的设备。但其系统误差随时间不断积累，不能长时间进行导航，车辆的机动能力将受到极大的制约[1,2]。目前车载组合导航常用SINS/GNSS组合导航的方式来实现车辆的高精度定位，由于全球卫星定位系统（GPS）信号容易被干扰，有可能暴露自身位置的风险，不能满足军事车辆对于自主性的要求[3]。里程计在车辆中随处可见，作为外部测量工具使用非常方便，将里程计测量的速度信息引入惯导系统，既能够保证车辆的自主性，又能够保证车辆的导航精度[4,5]。

在SINS/OD组合导航系统中，近年来的研究热点主要集中在惯导安装误差角和里程计误差补偿方面。文献[6]采用零速修正的方法进行里程计的标定，但需要间隔一段时间停一次车，降低了车辆的机动性；文献[7]通过向心加速度作为观测量进行滤波，但车辆实际运动环境复杂、噪声多，导致估计结果不准确，从而定位精度并不高；文献[8]利用车辆正常行驶过程中横向和法向速度为零的约束条件，考虑了惯导安装误差角，但没有考虑里程计刻度系数误差；文献[9]研究了INS/OD集成系统中里程计的测量模型，并采用多模型自适应估计方法进一步提高了定位性能；文献[10]利用非线性参数运动模型与地面真实训练数据之间的残差训练里程计误差的高斯过程模型参数，通过有效计算图像帧和有效分布关键帧来增强视觉SLAM；文献[11]提出了一种基于高斯过程回归（GPR）的里程计故障检测方法，采用粒子群优化方法寻找高斯模型的最优超参数，提高了导航精度。

为实现车载惯导的高精度自主定位，里程计的精确建模越来越重要，本文除惯导安装误差角和里程计刻度系数误差以外，研究了里程计截断误差对定位精度的影响，提出了基于里程计截断误差补偿的SINS/OD组合导航算法。通过分析里程计脉冲输出的误差特性，完善了传统的速度匹配组合导航算法，但考虑到以速度形式容易扩大误差，而里程计的输出与车辆运动特性有关，采取捷联惯导输出转化为脉冲增量输出与里程计输出做差作为量测的补偿模式，直接作用于里程计原始输出，效果是很理想的。前两种方法都是将里程计截断误差作为随机常值，利用卡尔曼滤波进行补偿，但局限于里程计正常工作，同时补偿可能不精确，为了改善性能，充分利用历史数据，提出基于高斯回归的里程计截断误差预测模型，该模型能够有效预测车轮里程计的测量残差，当里程计发生故障时也能很好补偿，大大提高了组合导航的精确度，三种算法由浅而深，逐层递进，都证明了补偿里程计截断误差的重要性。

1 SINS/OD组合导航系统

1.1 系统模型描述

如图1所示，陆地车辆配备有一个导航级的IMU，里程计安装在车辆非转向轴上。为了方便开展研究，需要对车载惯导/里程计组合导航系统坐标系进行定义。选取东北天为导航参考坐标系，记为n系；车体坐标系记为m系，其中车体中心 Om位于车辆前轴的中点，xm轴指向车体横向的右方，ym轴指向车体纵向的正前方，zm轴指向天向，里程计用累积的脉冲来测量车辆前进的运动，即从车辆运动开始时产生脉冲数，为了简单起见，可认为里程计坐标系与车体系一致；惯导坐标系记为b系，与车体坐标系指向一样，满足右手直角坐标系，但由于安装精度的影响，m系与b系之间存在安装误差角，分别记为俯仰误差角αθ、横滚误差角 αγ、航向误差角αψ。

1.2 里程计刻度系数误差分析

里程计输出是脉冲信号，在采样周期T内，里程计输出p个脉冲，令里程计刻度系数为K，则车辆行驶速度νD与脉冲满足以下关系：

假设车辆行驶过程中，车轮没有打滑和跳动，车辆天向和横向速度均为零，里程计能够准确测量车辆前进速度，里程计速度在车体坐标投影为：

然而车辆在实际运动中，里程计的刻度系数会受到车辆载荷、轮胎磨损、气压和温度等因素的影响发生变化导致测量误差[12]，设里程计的刻度系数误差为δk，则里程计真实速度为：

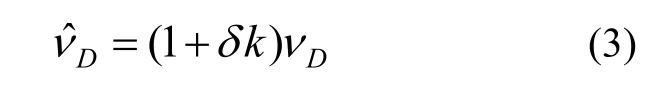
1.3 车载惯导安装误差角分析

由上述可知惯导存在安装偏差角，则惯导坐标系到车体坐标系的安装误差矩阵可以表示为：

式中c表示cos，s表示sin，由于安装误差角均为小角度，我们可认为cosαi=1、sinαi= 0，其中i=θ、γ、ψ，则有：

式中 α =[αθ0 αψ]T，可以看出横滚误差角αγ不影响里程计的速度测量值。实际建立的导航坐标系n'与理想导航坐标系n之间存在失准角φ= [φEφNφU]T，惯导坐标系到导航坐标系的转换矩阵为：

1.4 捷联惯导误差方程

根据文献[13]，直接列写出捷联惯导误差方程：

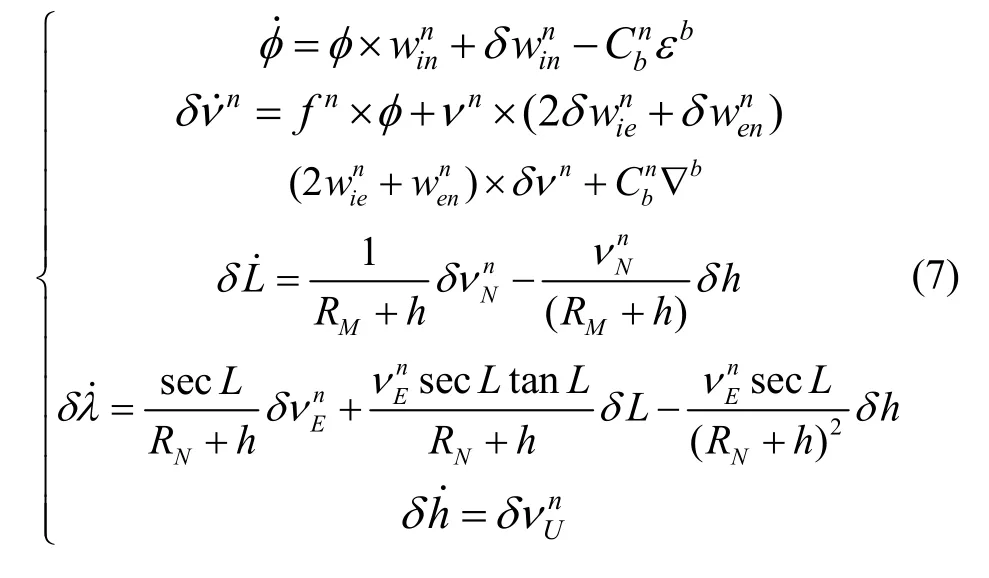
其中：φ为失准角；nν为车辆在导航系的运动速度；为导航系相对于惯性系的角速度在导航坐标系的投影；为地球自转角速度在导航系的投影；为导航坐标系相对于地球坐标系的旋转速度在导航系的投影；fn为加速度计比力输出在导航系的投影；εb为陀螺误差在惯导坐标系的投影；∇b为加速度误差在惯导坐标系的投影；L、λ、h分别为经度、纬度、高程； RM为子午圈主曲率半径；RN卯酉圈主曲率半径。

2 滤波算法

2.1 传统速度匹配组合导航算法

为了方便后续描述，本小节所述传统速度匹配组合导航算法称为Tv-kf（T：传统；v：速度观测；kf：卡尔曼滤波）。考虑里程计刻度系数误差和惯导安装误差角，车辆真实速度在导航系投影：

代入式(3)(5)(6)，忽略二阶小量有：

则里程计速度误差方程为：

式中ei表示第i个元素为1的单位列向量。将捷联惯导系统的姿态误差 φn，速度误差 δ νn，位置误差δPn，陀螺零漂 εb，加速度计零偏 ∇b，里程计刻度系数误差 δ k和惯导安装误差角αθ、αψ作为系统状态变量，共18维：

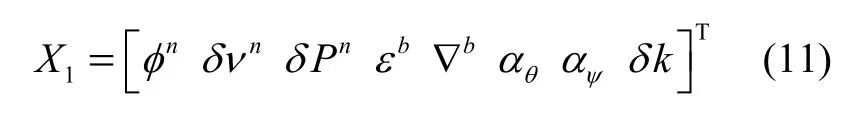
系统状态方程为：

式中，1F为状态转移矩阵，令F15×15是由式(7)推出的基本捷联惯导状态转移矩阵，具体公式在此不再赘述，则W1为系统噪声。选取捷联惯导与里程计输出的速度之差作为观测量，则有：

系统量测方程为 Z1= H1X1+ V1，V1为测量噪声，其中量测矩阵为：

2.2 基于速度观测的截断误差补偿算法

本小节所述基于速度观测的截断误差补偿算法称为Iv-kf（I：改进；v：速度观测；kf：卡尔曼滤波）。当考虑里程计脉冲截断误差时，设采样周期T内脉冲测量误差为δpod，车辆真实行驶速度为：

同理可得里程计速度误差方程：

将里程计截断误差δpod作为系统状态，为随机常值，利用卡尔曼滤波进行实时补偿，则系统状态变量为：

同样选取捷联惯导与里程计输出的速度之差作为观测量，则有：

由于系统状态变量增加了里程计截断误差δpod，则系统状态转移矩阵为因此系统量测矩阵变为：

2.3 基于脉冲观测的截断误差补偿算法

基于脉冲观测的截断误差补偿算法称为P-kf（P：脉冲观测；kf：卡尔曼滤波）。图2表示了里程计的测量模型，黑色点为脉冲发生节点，相邻两个时间差值为采样周期，则在任何一个采样时间段 (tk, tk+1)内，里程计真实脉冲值pK+1与测量输出值有如下关系：

图2 里程计测量模型Fig.2 Odometer measurement model

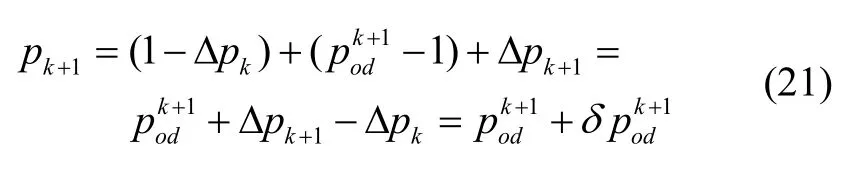
式中 δpk+1=Δpk+1-Δpk，为里程计测量的截断误差，取值范围为(-1,1)。

里程计脉冲输出与车辆运动状态有关，单位时间内车辆运动越快里程计脉冲输出个数越多，由于惯导设备精度高，能够准确反映车辆运动状态，则在相同采样时间段 (tk, tk+1)内，计算出车辆行驶时惯导所产生脉冲数为：

式中sk+1为车辆在采样时间内行驶的距离，分别为tk和tk+1时刻车辆在m系下的速度，为中点速度，为车辆行驶的加速度。

由于惯导测量存在误差，导致采样时间内车辆行驶距离与真实值存在偏差Δsk1+，则惯导输出转化为脉冲输出与里程计脉冲真实值pk+1有如下的关系：

联立式(21)(23)，可得以下关系：

由于非完整性约束，只有沿着车体前进方向有脉冲增量，采样时间 T = tk+1- tk很短，可认为为常量，因此在采样时间 (tk, tk+1)内惯导输出脉冲增量为：

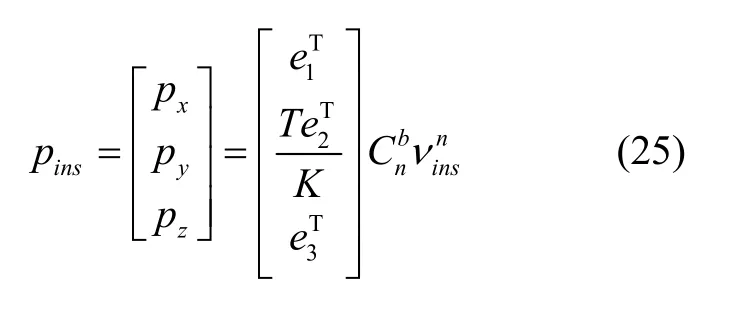
式中px、pz称为虚观测量，为车辆横向和天向的观测量；为惯导在导航系下采样时间段内的中点速度。由于里程计刻度系数误差和惯导安装误差角的存在，代入式(5)(6)，其真实脉冲为：

忽略二阶小量，由此可得惯导脉冲增量误差为：

选取惯导脉冲输出与里程计输出之差作为观测量：

同样将里程计截断误差作为随机常值，引入到系统状态变量中，则有：

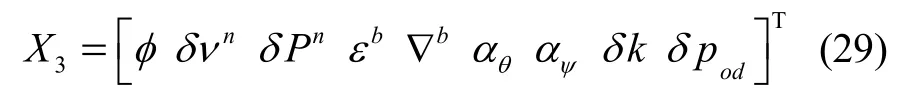
而系统状态转移矩阵 F3=F2，因此可得系统量测矩阵为：

2.4 基于高斯回归模型的截断误差预测

基于高斯回归模型的截断误差预测算法称为Gp-kf（G：高斯回归；p：脉冲观测；kf：卡尔曼滤波）。在2.3节中，详细介绍了里程计脉冲输出和惯导脉冲的误差模型，将里程计截断误差作为随机常值利用卡尔曼滤波进行补偿，可能补偿不够精确，同时里程计发生故障会产生较大误差。高斯过程（GPs）是一个强大的非参数工具，用于从样本数据学习回归函数，可以很好地处理糟糕和嘈杂的数据，因此在解决现实场景时非常实用。由式(24)可知，惯导脉冲输出减去里程计输出等于里程计误差加上惯导脉冲误差，在标准的卡尔曼滤波中，模型的量测误差主要是噪声引起的，因此惯导脉冲的测量误差 δpins亦可认作为零均值高斯白噪声。因此，有了以下的带噪声的高斯模型：

式中x表示输入向量，在此系统中用里程计输出的脉冲pod来描述；f(x)是函数在x处的真值，即里程计误差；y是被噪音污染的观测，即惯导脉冲输出减去里程计脉冲输出；噪声ε是服从 N(0,σn2)的高斯分布，即惯导脉冲误差 δpins。

下面将详细介绍如何利用高斯回归模型对里程计误差进行预测。已知输入向量集合 x = [x1x2…xn]和带噪声的输出集合 y = ［ y1y2… yn］，对于新的输入x*，为了得到最小噪声的预测输出f(x*)，可以得到已知观测x的先验分布和预测点x*与已知观测x的联合分布分别为：

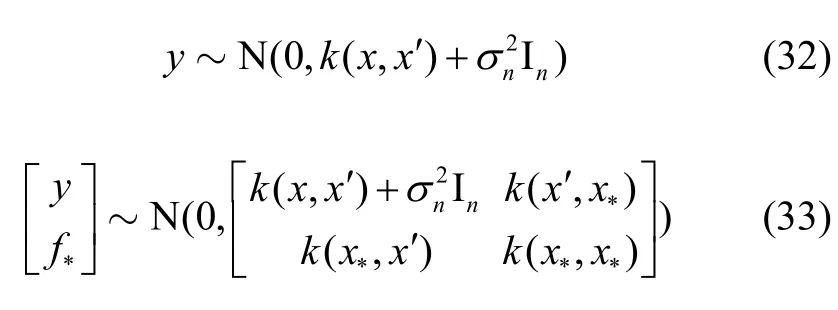
式中In为n维单位向量，k(x,x')为协方差矩阵，用于度量 xi与xj之间的相关性；k(x*,x')是预测点x*和已知观测x之间的协方差矩阵； k(x*,x*)是预测点本身的协方差。即为以下公式：

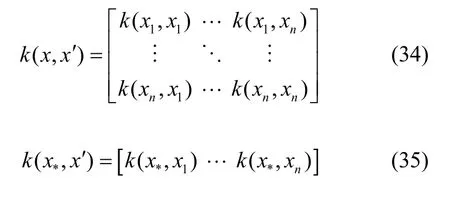
高斯回归是一种非参数模型，没有训练模型参数的过程，一旦协方差函数、输入数据给定，则模型就被唯一确定下来。所以，回归的重点在于确定协方差函数。协方差函数有多种，通过对模型的分析，选择SE核函数，其表达式为：

式(36)的超参数为未知参数，当l选择越大，函数更加平滑，同时训练数据点之间的预测方差更小，反之l越小则函数更加“曲折”，训练数据点之间的预测方差更大；σ则直接控制方差大小，σ越大方差越大，反之亦然[14]。如何选择最优超参数，即在最优超参数下y出现的概率为最大化，可通过用极大似然法求解，多元高斯分布的负对数边际似然函数为：

先选择合适的超参数初值，然后通过式(37)可以求解出最佳超参数，就能得到协方差函数k(x,x)的具体表达式，从而求解高斯过程回归的关键预测方程：

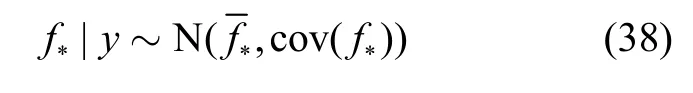
其中：

由上述分析得到了基于高斯回归模型的里程计截断误差预测值，在下一步进行滤波时，有如下观测方程：

由于里程计截断误差已经在观测量中进行了补偿，则系统的状态变量为：

系统状态转移矩阵 F4=F1，因此量测矩阵为：

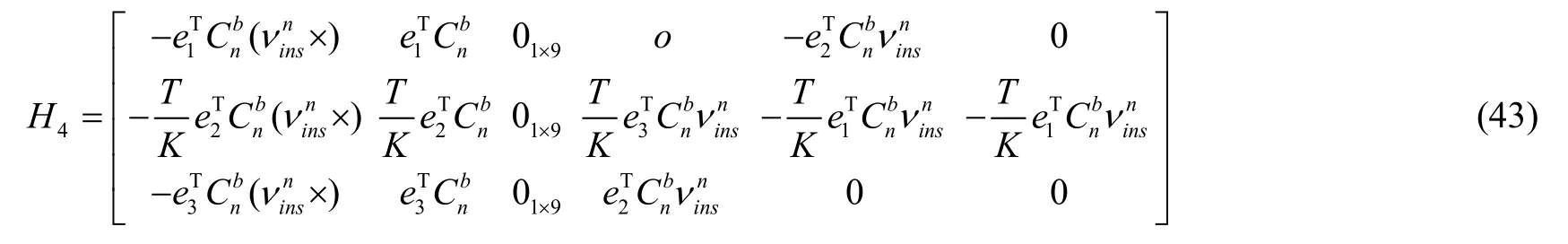
故障诊断：将惯导输出转化为脉冲，可以轻易的判断里程计工况是否正常，假设测量速度误差在m系下为±2m/s（很大了），则由式(22)可知惯导产生的脉冲误差为：

式中采样周期T和里程计刻度系数K均为实验真实值，可真实惯导引起的脉冲误差是很小的，远远小于1个脉冲。通过里程计误差输出模型，得知截断误差 δpod∈(-1 ,1)，因此有以下判断基准：

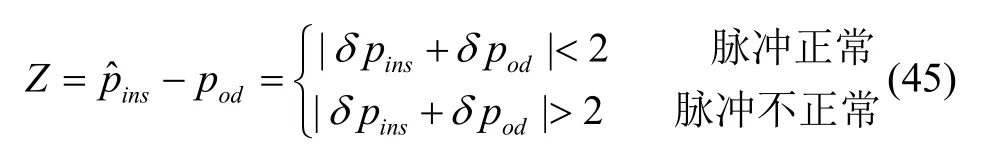
当发生故障时，里程计脉冲输出不可信，由故障诊断条件可知，正常工作情况下两者之间的脉冲差值小于2个脉冲，所以在短时间内可取惯导脉冲输出的整数部分作为里程计输出是可行的，目的是减小因故障产生的较大观测误差，从而在一定程度上减小定位误差。

3 仿真与车载实验

3.1 仿真试验与分析

为了验证所提方法的性能，进行了仿真试验。设定车辆初始位置：经度108.909°E，纬度34.246°N，海拔高度为380m。车辆初始速度为零，模拟了车的运动状态，具体包括：①静止100s后，沿正北方向以1m/s2的加速度行驶10s，然后匀速直线行驶200s；②以2°/s的角速度左转90°，之后行驶200s；以2°/s的角速度左转90°，之后行驶200s；③以 -1 m/s2的加速度行驶5s；④以2°/s的角速度左转450°，之后行驶200s；⑤以2°/s的仰角速度爬升10s，之后行驶200s；以2°/s的俯角速度下行10s，之后行驶20s；⑥以3°/s的角速度左转90°，之后行驶200s⑦以1m/s2的加速度行驶5s，之后行驶200s；⑧以2°/s的角速度左转90°，之后行驶300s。

设定惯性元件参数：陀螺仪零偏为0.01°/h，随机游走为0.001°/，加速度计常值漂移为50μg，随机游走为5μg/，输出频率为100 Hz。初始姿态角均为零，惯导安装误差角为俯仰安装误差角αθ为20'、航向安装误差角αψ为30'，里程计刻度系数误差为0.02，为了仿真里程计截断误差，在里程计脉冲输出加上随机误差。车辆运动轨迹如图3所示，行驶时间约为37 min，轨迹共长17.25公里。

图3 仿真轨迹Fig.3 Simulation trajectory

惯导安装误差角和里程计刻度系数误差在线标定结果如图4所示。从图中可以看到，所提方法都能够较准确地估计惯导安装偏差角，补偿截断误差的速度匹配组合导航在俯仰安装误差角估计上精确度差了些；由于里程计输出加了随机误差，刻度系数误差都在0.02左右。（俯仰安装误差角只影响高度误差，航向安装误差角影响水平定位误差）。

图4 仿真试验在线标定结果Fig.4 Online calibration results simulation test

以仿真的SINS/GPS为定位基准，四种组合导航算法解算的水平定位误差结果和定位误差随里程变化所占百分比结果如图5所示。从图中可以看到，所提的三种截断误差补偿算法较传统速度匹配组合导航在定位精度上都有不同提升，验证了算法的有效性。

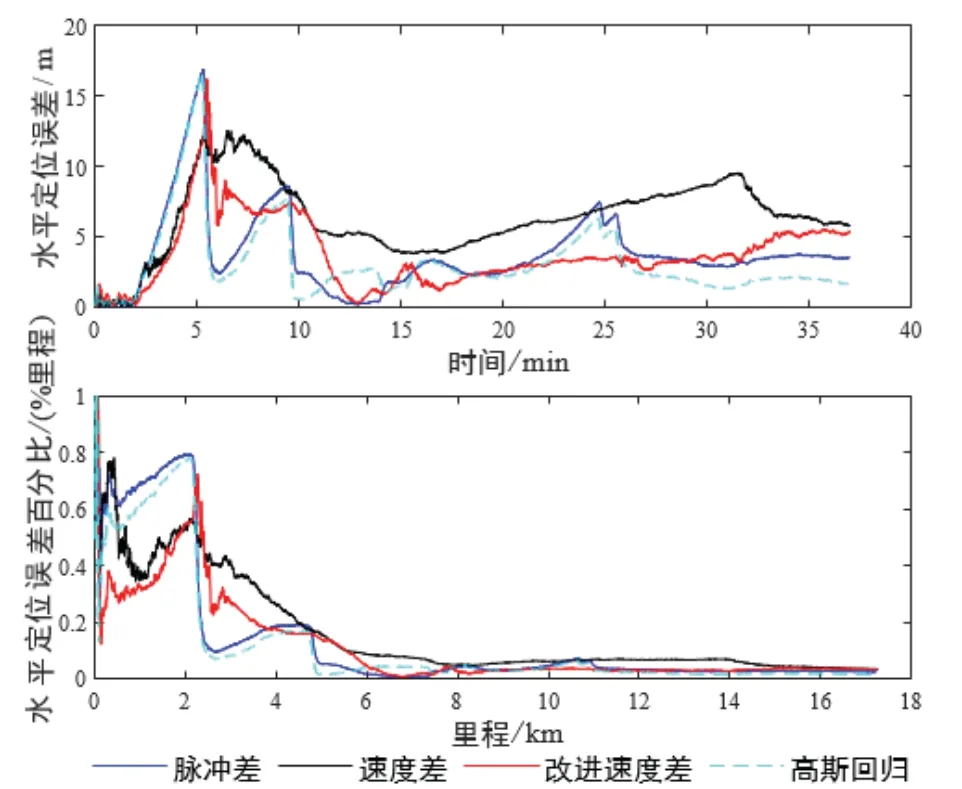
图5 仿真试验水平定位误差结果Fig.5 Horizontal positioning error results of simulation test

为了更客观对比所提算法的性能，对图5水平定位结果的均方根误差（RMSE）以及RMSE占总行驶里程的百分比进行了量化统计，如表1所示。传统速度匹配组合导航的RMSE为5.8542 m，在速度观测中补偿里程计截断误差后提升了0.5437 m的定位精度；而基于脉冲观测滤波补偿的RMSE为3.5127 m，实现了定位精度的较大提升，基于脉冲观测的高斯回归模型预测显示了它的优越性能，提升到了1.5936 m，两种算法的RMSE相对传统算法分别减少了40%和72.78%。

表1 仿真水平定位误差结果统计Tab.1 Statistics of simulation horizontal positioning error results

3.2 实验验证

本文还通过车载实验来验证算法的实际性能，该实验车配备有高精度激光惯导、轮式里程计和GPS，如图6所示。

图6 实验装置Fig.6 Experimental device

IMU的输出频率为200 Hz，其陀螺仪零偏为0.005°/h量级，角度随机游走系数为0.0005°/h水平；加速度计零偏为50μg量级；里程计输出频率为200 Hz，精度为0.1%，按照传统平直路线起点终点方式标定，得到里程计刻度系数 K= 0.013034m/脉冲，以航位推算和GPS组合得到惯导的安装偏差角αθ= 28.88'、 αψ=-2 4.14'；GPS接收机定位精度为5 m，输出频率为1 Hz。本次进行了较长里程的跑车实验，行车时间总计为80 min，总行程143.18 km，图7为本次实验的行车轨迹。

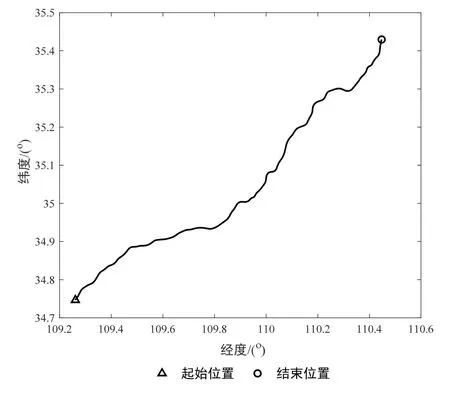
图7 行驶轨迹Fig.7 Traveling track

按照上述方法对惯导安装误差角和里程计刻度系数误差在线标定补偿，得到车载实验的误差参数如图8所示。由图8可知，P-kf滤波补偿算法和Gp-kf估计更精确，收敛也快；补偿里程截断误差的速度匹配组合导航前期相对传统算法估计更精确一些，后期也能较准确地估计安装误差角；里程计刻度系数误差受诸多因素影响，变化无规律，每个算法补偿也有差异。

图8 车载实验在线标定结果Fig.8 On line calibration results of vehicle-mounted experiment

如图9所示，为捷联惯导与里程计脉冲输出的差值统计图，横坐标为误差范围，纵坐标为不同误差所占脉冲个数，由图9可以看出，两者之间的脉冲差值的绝对值大多数要小于2个脉冲，所以整个跑车过程里程计工作状态良好，当差值的绝对值大于2时，可判断里程计输出不可信，采用发生故障时的补偿方法。

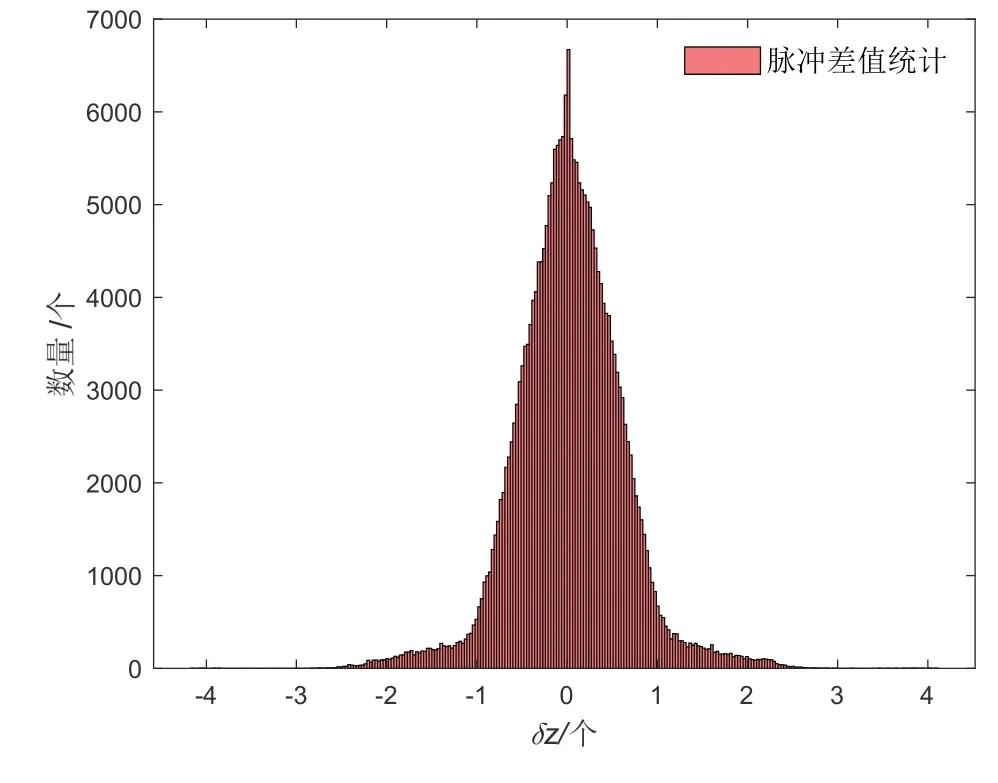
图9 惯导与里程脉冲输出差值统计图Fig.9 Statistical diagram of difference between inertial navigation system and odometer pulse output

以跑车的SINS/GPS组合导航为定位基准，四种组合导航算法解算的水平定位误差结果和定位误差随里程变化所占百分比结果如图10所示，统计结果如表2所示。在140多公里的行程中，传统速度匹配组合导航水平定位误差为174.6372 m，在传统速度匹配组合导航中补偿里程计截断误差后就变为159.7581 m，减少了8.52%的定位误差，可见补偿里程计截断误差是很有必要的。基于脉冲观测的滤波补偿和基于高斯回归模型预测的方法凸显了其良好性能，虽然采用的是标准的卡尔曼滤波，但水平定位误差相对于传统速度组合导航分别减少了82.42%和87.09%（注：基于脉冲观测，但未补偿里程计截断误差的RMSE为46.37 m，图10中未画出），归结原因有两个：其一，考虑了里程计的截断误差，建模更加完整，同时在航向角的估计上更加精准；其二：量测的不同，传统的速度观测对里程计输出进行了微分处理，扩大了误差，以脉冲观测的形式直接作用里程计原始输出，利于滤波。但基于脉冲观测的滤波补偿在40 min-50 min期间是优于高斯回归模型预测的，由于高斯回归模型预测的可靠性取决于超参数，对数据的拟合程度是有置信区间，而在此时段对里程计截断误差的拟合效果较差，虽然提出基于高斯回归模型预测里程计截断误差的算法，验证了其可实施性，但并不是一劳永逸的，需要继续对里程计截断误差做更深入研究。

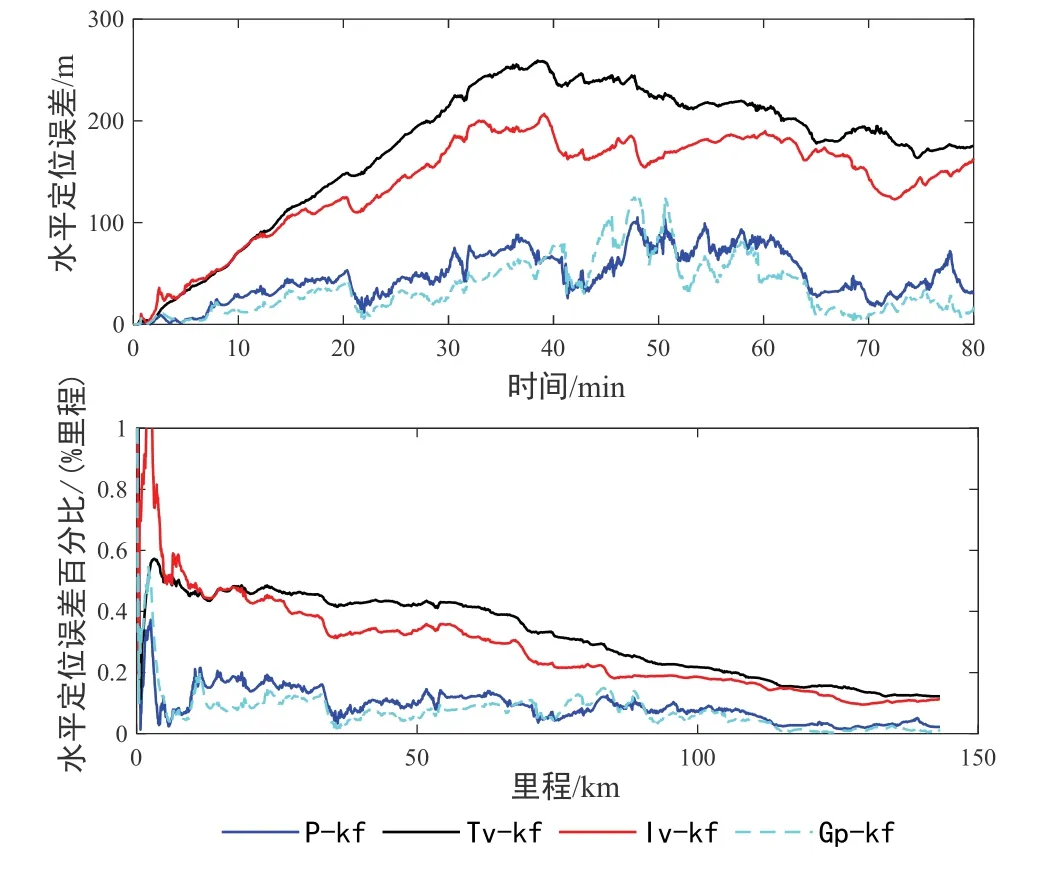
图10 水平定位误差结果Fig.10 Horizontal positioning error result

表2 水平定位误差结果统计Tab.2 Statistics of horizontal positioning error results

4 结 论

本文对车载惯导与里程计的组合导航进行了研究，重点分析了里程计脉冲输出的误差特性及其补偿算法。具体地说，在里程计刻度系数误差和惯导安装误差角的基础上考虑里程计脉冲测量误差，制定了三种不同补偿算法，仿真试验和跑车实验结果都表明，补偿里程计截断误差后的速度匹配组合导航较传统速度匹配组合导航在定位精度上能有效提升，验证了其补偿里程计截断误差的重要性。同时，针对传统算法的不足，提出效果更好的基于脉冲观测的截断误差补偿算法和基于高斯回归的截断误差预测模型，两种算法全程水平定位误差均低于0.2%，有较高的定位精度，所提出的方法具有工程应用价值。