基于双轴旋转调制惯性测量的载体导航信息提取方法
2022-09-26江一夫李四海严恭敏
江一夫,李四海,严恭敏,谢 波
(1. 西北工业大学 自动化学院,西安 710029;2. 西安航天精密机电研究所,西安 710100)
旋转调制技术由于其低成本、高效的误差抑制机理和系统实现方法,已经发展成为长航时高精度自主导航的核心关键技术[1-3]。但双轴旋转惯导在旋转过程中尤其是基于实时隔离控制的混合式旋转调制[4,5]过程中无法直接从原始惯性测量信息中准确提取载体角速度和加速度等导航信息,但二者对于基于旋转惯导的飞行控制以及基于载体系惯性测量的自主式行进间对准都是不可或缺的[6]。将旋转调制惯性导航信息转换为与载体固联的导航信息的过程也可称为解调过程[7]。本文注重于原始惯性测量单元信息的解调,提出了一种以精确标定惯性测量单元与内外框时空关系来实现原始惯性测量信息解调的方法,目标是将动态旋转惯性测量输出等效为静态物理壳体输出,从外部角度来看,其对外输出惯性测量信息与无旋转机构的捷联惯导一样,但是内部依然在实现旋转调制误差自补偿。
目前查阅到的文献仅关注惯性测量与内外转轴之间安装角的标定方法。文献[8]推导了固定转位角度下由地理系方向余弦矩阵计算安装角的公式,文献[9]提出了薄壳算法对两者之间安装角进行标定;标定精度与陀螺非正交安装角的精度相当;文献[10]采用统一的卡尔曼滤波方法对惯性测量组合相对内外转轴的安装角进行了精确标定。本文从内外框坐标系的定义出发,利用正反旋转求取的转轴方向矢量以及矢量之间的共面关系,提出了一种简单可靠且综合考量了整圈所有角位置状态的安装角标定方法。事实上,除安装角这一空间关系外,转轴的锥摆运动可能导致其循椭圆轨迹旋转,测角信息不能反映真实的旋转角度,因此需要同时对测角信息本身的不圆度误差进行标定补偿。另外,惯性测量单元与转位测角之间存在小量时间不同步误差,这对角加速旋转过程的载体导航信息提取而言,可产生明显的影响,因此进一步对两者之间时间不同步误差进行了精细化标定和补偿。
1 坐标系定义
对于包含内外旋转框架的捷联惯导系统,定义三个陀螺的敏感轴分别为xg、yg和zg,定义三个加速度计的敏感轴为ax、ya和za,定义惯性测量坐标系p、内框坐标系s、内框零位坐标系s0、外框坐标系d系、壳体坐标系b系,这些坐标系的关系如图1所示,其原点位于内外框转轴的交点。
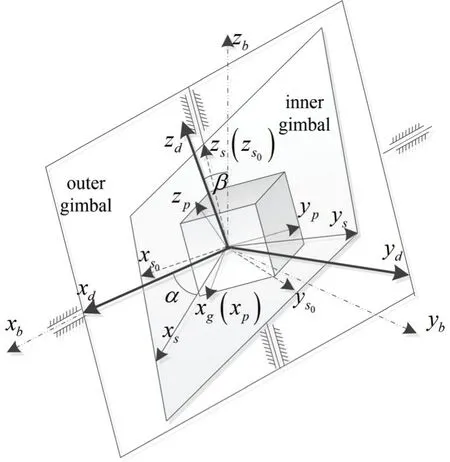
图1 坐标系定义Fig.1 Coordinate frames definition
惯性测量坐标系p:xp与陀螺敏感轴xg同向,yp位于xgyg平面上,并垂直于xp,zp与xp、yp成右手直角坐标系。
内框坐标系s:zs与内框转轴重合,xs与惯性测量坐标系xp轴在zs垂直平面的投影重合,ys与zs、sx构成右手直角坐标系。惯性测量坐标系固联于内框架,跟随其一起旋转,两者之间的小角度安装矩阵可表示为。
内框零位坐标系s0:即内框转轴位于零位时的内框坐标系,设内框转角为α,则有。

外框坐标系d:xd与外框转轴重合,yd与内框零位坐标系ys0在转轴xd垂直平面的投影重合,zd与xd、yd构成右手直角坐标系。内框零位坐标系与外框架固联,跟随外框一起旋转,两者之间的小角度安装矩阵可表示为
载体坐标系b:将外框轴在零位时的外框坐标系定义为载体坐标系。其与惯导系统物理壳体和载体固联。当外框转角为β时,有:

导航坐标系n,xn和yn轴位于当地水平面,且xn指东,yn指北,zn沿地垂线指上,即东北天地理坐标系。
2 载体系惯性测量数据的转换计算方法
在惯性测量误差已经经过精确标定,即不会由于旋转调制过程的正反旋转、上下停驻等产生额外惯性测量误差的基础上,可以将惯性测量坐标系角增量和速度增量解调还原到载体坐标系,如式(3)所示。

其中, Δθp(tk)和表示惯性测量坐标系角增量和速度增量,Δ θb(tk)和表示载体坐标系角增量和速度增量,由测角信息计算得到。
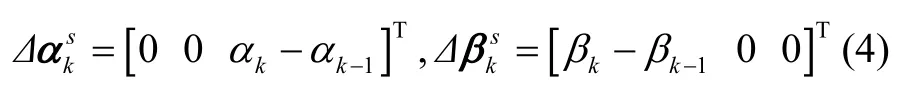
式中,αk、αk-1、βk和βk-1为当前采样时刻与前一采样时刻的内外框测角信息。
可见,要实现惯性测量信息的精确解调和载体系导航信息的提取,关键在于小角度安装矩阵和的精确标定,以及转位测角 kα和 kβ的实时准确获取。
3 惯性量与内外转轴时空关系的标定
3.1 惯性测量单元与内外转轴安装角标定
惯性测量单元与内外框安装角,采用内外框正反整周旋转的标定方式。首先锁定外框,驱动内框正反整周旋转,设正反转陀螺原始输出脉冲累加和分别为转换到惯性测量坐标系后为:

则内框绕其zs旋转轴单位矢量在惯性测量坐标系的投影:
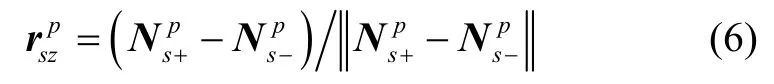
如图2所示,根据内框坐标系定义,s系的xs轴为p系xp轴在zs轴垂直平面上的投影,故s系的zs轴、xs轴和p系的xp轴三轴共面,这一平面任意不共线两个矢量的叉乘必然与这个平面垂直。取为其中一个矢量,沿xp轴的单位矢量为另一个矢量,则s系ys轴的单位矢量在p系的投影为:
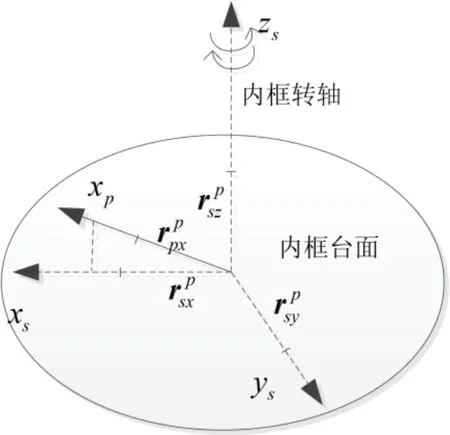
图2 惯性测量坐标系、内框坐标系和内框转轴的关系Fig.2 Relationship of inertial-measurement frame,inner-frame and its rotating axis
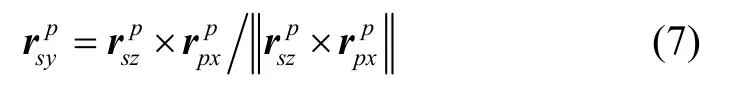
根据右手法则,可以计算出xs轴在p系的投影矢量
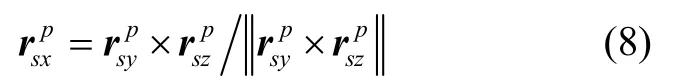
由此可以得到惯性测量坐标系p系到内框坐标系的转换矩阵:



图3 内框零位坐标系、外框坐标系和外框转轴的关系Fig.3 Relationship of start-point inner frame, outer-frame and its rotating axis
根据外框坐标系定义,yd与内框零位坐标系ys0在转轴xd垂直平面的投影重合,故d系的xd轴、yd轴和s0系的ys0轴三轴共面。因此有:
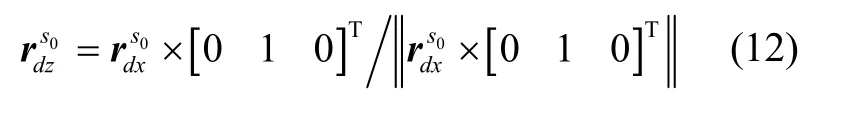
同理可得:

至此完成惯性测量单元与内外转轴安装角关系标定。
3.2 惯性测量与转位测角不同步时间标定
设转动过程中tk采样时刻的内框转位测角为 kα,内框测角不同步时间为δtps,陀螺测量的tk时刻内框坐标系转位角速度为由于内框绕zs轴转动,因此有:

本质上所有时刻的 αk-α0构成一条转位测角增量曲线,所有时刻的构成一条惯性测量角增量曲线,两条曲线是相似的,利用其相似平移原理可以求得两者之间的时间不同步。因此将式(15)改写成最小二乘的形式,有:
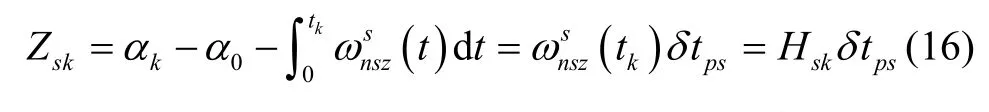
同理,设外框转位测角为 βk,外框测角不同步时间为δtpd,在内框锁紧,在外框正反旋转过程中有,其相对地理系的旋转角速率可以表示为:

求解惯性测量与外框不同步时间的最小二乘方程可以表示为:

利用正反旋转过程中实时测角信息和陀螺测量信息可以建立递推最小二乘方程实现惯性测量与内外框转位测角不同步时间δtps和δtpd的估计。
为了实现测角不同步时间的准确补偿,要求测角信息具有较高的采样频率。一般而言,惯性测量会延迟于转位测角,不同步时间可能包含数个测角周期Δtα,且不是测角周期的整数倍。图4以内框为例,说明了测角不同步时间的补偿方法,其中 αk表示当前时刻的内框测角,表示 δtps/Δtα向下取整,保存n+1长度滑动窗口的测角信息αk-n~ αk,最小二乘估计出测角变化率kα,而经延时补偿后的惯性测量时刻点往往位于相邻两个测角采样点中间,利用测角信息αk-n和测角变化率外推获取当前惯性测量时刻对应的转位测角信息即:
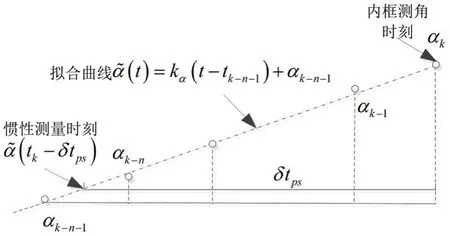
图4 惯性测量与转位测角之间时间不同步误差的补偿方法Fig.4 Compensation method of time synchronization between inertial measurement and rotation angle measurement

式中 rem (δ tps,Δtα)表示不同步时间δtps对测角周期Δtα取余数。
3.3 转位测角不圆度标定
理论上,经过安装角和时间不同步误差补偿后,按照式(3)将原始惯性测量数据解调到载体系进行惯性导航解算,当载体保持静止时,无论内外框如何转动,其三维姿态角应该保持不变。但实际中转轴方向姿态角仍然存在一定的类三角函数波动误差,这是由于转位机构安装间隙等原因,转轴并非按照圆形轨迹旋转,测角信息不能反映真实的旋转角度,需要对该误差进行补偿。将该误差拟合成式(20)所示谐波函数。

其中δψk表示内框轴旋转时载体系航向角波动误差,a0,a1,b1, … a6,b6为内框测角不圆度各次谐波系数,表示经过时间不同步补偿的内框测角,δkθ表示外框轴旋转时载体系俯仰角波动误差,c0,c1,d1, … d6,d6为外框测角不圆度各次谐波系数,表示经过时间不同步补偿的外框测角,利用转位过程求得的实时惯性导航误差和实时测角,采用递推最小二乘方法可以实现各次谐波系数的估计。实时补偿时,采用式(21)计算得到经过不圆度误差修正的内框测角和外框测角。

4 试验验证
理论上,载体静止条件下,原始惯性测量信息经解调还原到载体系后,内外框旋转过程导航姿态应该趋于平稳,不存在波动误差,因此试验验证中以载体系导航解算姿态波动误差的大小来考核导航信息提取精度。如图5所示,基于光纤陀螺双轴旋转惯导,按照内框正反各一圈、外框旋转到-180°、外框正反各一圈的流程采样旋转数据进行验证。其中光纤陀螺百秒标准差约为0.002 °/h(1σ)和加速度计百秒标准差约为20 µg(1σ)和转位机构测角精度2"(1σ),采样周期为1 ms,旋转速度设定值为5 °/s。

图5 验证试验中陀螺脉冲Fig.5 Gyro pulse in validation test
惯性测量与内外框转位测角的时间不同步误差补偿效果分别如图6和图7所示。从图中可以看出,时间不同步误差会造成旋转过程姿态角的整体偏移,尤其是旋转加减速阶段,会造成所得载体系姿态角的突变,这在图7第一个子图中表现得尤为明显。而经过外框不同步时间补偿后,如图7第二个子图所示,旋转加减速阶段的误差突变消失,正反旋转过程姿态误差也趋于对称,但仍存在与角度大小相关的姿态误差,这里将其归结为测角不圆度误差。由于从图6中没有发现内框存在明显的不圆度误差,图8中仅给出了相应的外框测角不圆度误差补偿结果,补偿后明显消除了类三角函数的波动误差。
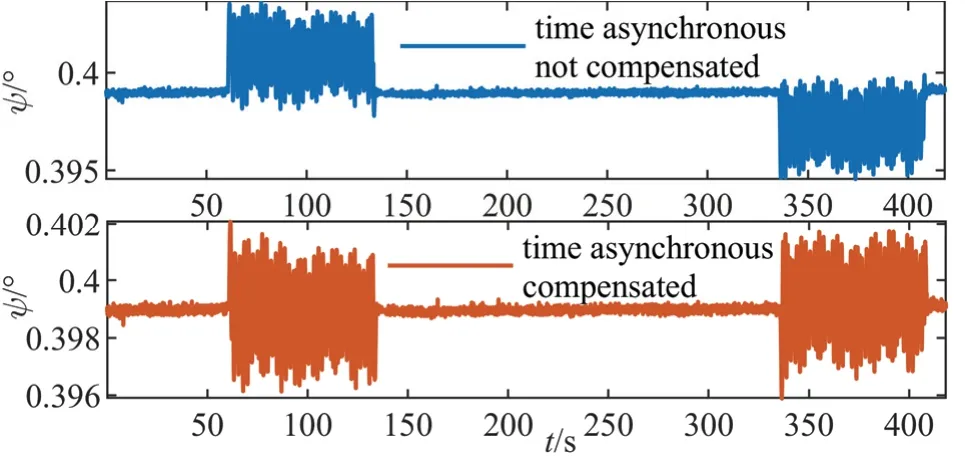
图6 内框测角时间不同步误差补偿前后的航向角Fig.6 Azimuth before and after compensation of inner-framework angle-measurement time-asynchronous
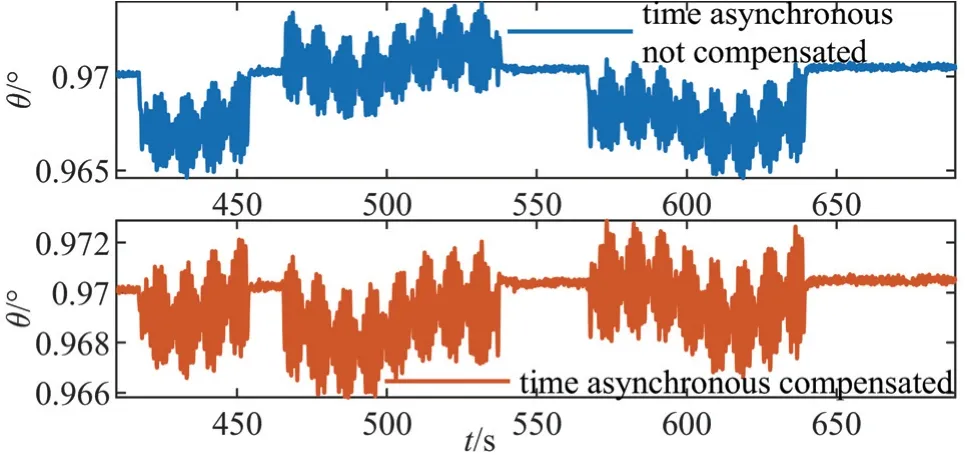
图7 外框测角时间不同步误差补偿前后的俯仰角Fig.7 Pitch before and after compensation of outer-framework angle-measurement time-asynchronous
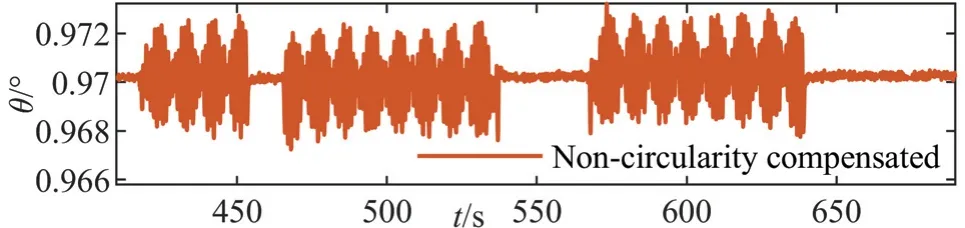
图8 外框测角不圆度补偿后的俯仰角Fig.8 Pitch after compensation of outer-framework non-circularity
最后在补偿时间不同步误差和测角不圆度误差的基础上,验证惯性测量与内外转轴之间安装角关系的补偿效果。当忽略惯性测量与内外转轴安装角,即认为且=I3×3时,转换到载体系的姿态和航向存在较大波动,具体如图9所示。经过安装角补偿后姿态和航向如图10所示,图中可见,旋转轴方向姿态角在旋转过程存在峰峰值0.005 °的噪声误差,这与采样周期和旋转速率的乘积正好相当,若要进一步降低噪声幅度,需要进一步提升采样频率。
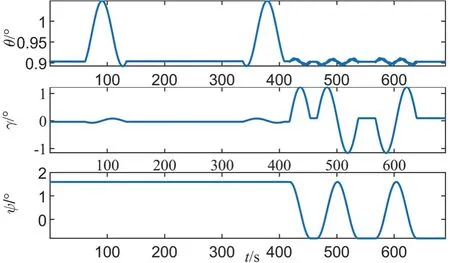
图9 转位安装角补偿前的载体系姿态角Fig.9 Body frame attitude before rotational installation angle compensation

图10 转位安装角补偿后的载体系姿态角Fig.10 Body frame attitude after rotational installation angle compensation
除去旋转过程旋转轴方向姿态角外,其他姿态角存在幅值约为0.001 °的毛刺状随机误差,这是由于双轴转位机构电锁控制误差和转轴间隙导致的小量晃动误差。如果不考虑这些随机误差,经误差补偿后,载体系姿态角基本处于稳定状态,波动幅度小于0.001 °,实现了角速度测量信息到载体系的精确转换。
值得说明的是,图10中结果是在精确标定惯性测量参数的基础上得到的,仅保证了原始惯性测量向载体系惯性测量的转换精度达到0.001 °,随着时间的推移,惯性测量参数必然发生变化,则彼时最终载体航姿提取精度取决于惯性测量单元本身的精度,而其转换误差仍然可以忽略不计。
5 结 论
基于全面、精细的误差模型,本文提出了一种基于双轴旋转惯性测量信息解调的载体系进行载体导航信息提取的方法。试验结果表明,所提出的转换方法能将旋转调制过程中的载体航姿误差控制在0.001 °以内,实现了高精度的载体航姿信息提取。在工程应用方面,旋转调制惯导不但可以维持其长航时高精度自主定位优势,也能为弹、车、舰等载体提供即时角速度信息和姿态、方位基准信息。另外,载体航姿信息提取方法的应用也能推动旋转调制惯导与里程计、测速仪等航位推算传感器之间组合导航技术的发展,使更高精度自主导航成为可能。
