非对称冗余惯导的在线标定与容错估计反馈策略

肖 烜，卢建睿，张永炎，沈 凯

（北京理工大学 自动化学院，北京 100081）

惯性导航系统（Inertial Navigation System, INS）不需要依赖外部信号就可以实现运动信息的输出，使得它成为了所有组合导航系统的公共参考信息提供者。众多组合导航系统都认为其内部的INS不会发生故障，时刻都能提供可靠的输出[1,2]。因此组合导航的性能高度依赖于系统内惯性元件的可靠性。当单一INS的可靠性无法保证时，飞行器、船舶和高价值地面车辆会安装两套以上的惯性测量单元（Inertial Measurement Unit, IMU）构成冗余惯性导航系统[3,4]，以提供可靠的惯性信息。

常规的冗余惯性技术使用多个规格相同的IMU以斜置的硬件结构实现[5,6]，容易受到装配难度和成本等的限制无法广泛应用。为此，考虑使用非对称冗余的方法实现惯性导航信息的高可靠性输出。本文设计的非对称冗余惯性导航系统（Asymmetric Redundant Inertial Navigation System, ARINS）由两套精度不同的INS构成，其中高精度INS在系统无故障的场景下被选作为基准信息输出，并被用来对低精度INS的误差进行在线标定；在高精度INS故障场景下，标定结果将被用来对低精度INS进行校正，然后利用低精度INS输出导航解算参数。

对于理想假设条件下的线性系统，Kalman滤波可以获得未知参数的最优估计。文献[7]利用单轴旋转调制微机电IMU滤波估计固联微机电IMU的器件零偏后由固联IMU输出舰船姿态，避免了旋转调制下的姿态输出锯齿状误差。我国嫦娥探月工程也使用滤波的方法在地月转移与月面上升等阶段对IMU进行在轨标定[8]。文献[9]基于误差参数动态估计的思路实现了对两套旋转调制惯导的在线故障监测。然而，Kalman滤波必须假设系统过程噪声与量测噪声服从零均值高斯分布，系统一旦发生故障，过程噪声或者量测噪声将会偏离假设条件，导致滤波性能下降甚至发散。为了解决这类问题，研究者提出了众多自适应Kalman滤波算法，试图对滤波模型中的过程噪声和量测噪声进行辨识[10,11]。其中，基于变分贝叶斯近似方法的自适应Kalman滤波近些年逐渐被研究人员关注[12,13]，它可以在每一个时刻以迭代而不是递推的形式识别缓慢变化的噪声。

针对本研究中的ARINS，考虑两套惯导之间的安装误差角、MEMS陀螺常值漂移以及MEMS加速度计的常值零偏，使用两套惯导之间输出姿态与速度之差作为量测量建立了在线标定模型，设计了基于序贯结构的变分贝叶斯自适应Kalman滤波（Variational Bayesian Adaptive Kalman Filter, VB-AKF）以实现对MEMS-INS误差的估计，给出了一种动态滤波收敛度分析方法，提出了一种基于收敛度的估计精度量化评价算法并以此为依据对MEMS-INS进行校正。仿真结果表明校正后的MEMS-INS水平位置误差发散趋势得到明显抑制，验证了本文提出的在线标定和容错估计反馈策略可以有效提升非对称冗余惯性导航系统的可靠性与精度。

1 非对称冗余惯性导航系统总体结构

1.1 结构描述与坐标系定义

本文设计的非对称冗余惯性导航系统如图1所示。作为基准系统的FOG-INS（FINS）与辅助备份系统MEMS-INS（MINS）共同安装在一个刚性基座上，L为两套INS之间的相对距离即杆臂，在此安装方式下杆臂可以视为是已知常量或忽略不计，并且不考虑刚性基座的弹性形变。

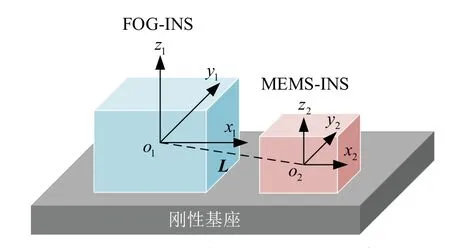
图1 非对称冗余惯性导航系统示意图Fig.1 Asymmetric redundant inertial navigation system

定义载体坐标系（b系）为载体的“右-前-上”方向，其中 o1x1y1z1是FOG-INS的载体系bf，o2x2y2z2是MEMS-INS的载体系bm；导航坐标系（n系）定义为“东-北-天”方向，表示为 oxnynzn。

由于实际系统安装误差的存在，bf系与bm系之间不重合，定义安装误差角为 μ=[μx, μy, μz]T，它通常满足小角度假设，则bf系与bm系之间的变换矩阵可以表示为：

1.2 非对称冗余惯性导航系统算法框架

对系统中两套惯导的故障检测，本文将使用文献[14]中提出的基于分段处理的序贯概率比检验（Sequential Probability Ratio Test, SPRT）算法完成。ARINS的算法框架如图2所示。VB-AKF估计MINS的误差参数并反馈其中的导航误差，分段SPRT算法检测到故障后，反馈策略基于估计量化评价补偿MEMS器件误差，故障隔离方法输出合适的惯性导航信息。为了简化分析，本文将只考虑FINS存在故障的情况。

图2 非对称冗余惯性导航系统算法框架Fig.2 The algorithm framework of the ARINS

2 容错在线标定方法总体设计

2.1 系统模型的建立

选择MINS的失准角φ、速度误差δV、位置误差δP、相对于FINS的安装误差角μ、陀螺漂移ε和加速度计零偏∇作为状态变量（每个变量包含3个维度的分量，因此X共18维）：

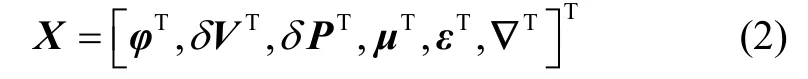
MINS姿态误差方程可表示为：

速度和位置误差方程可以表示为：

式(3)(4)(5)中对应矩阵Mii(i = a, v, p)的形式可以通过惯导误差方程得到。安装误差角、MEMS陀螺漂移和MEMS加速度计零偏视为常量：

状态方程可以写为：

其中， F ∈R18×18为状态转移矩阵； w ∈R6为系统过程噪声，此处可以认为是MEMS惯性元件的角度和速度随机游走， G ∈R18×6是噪声传递矩阵：

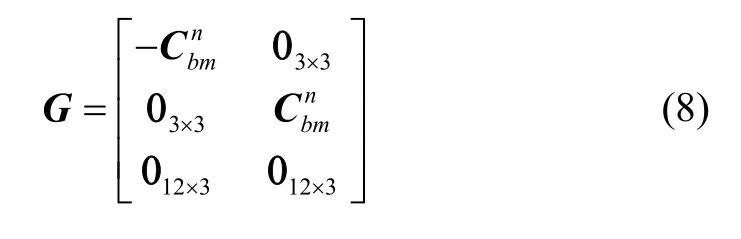
在线标定模型中的量测方程可以通过匹配两套INS的姿态和速度信息来构建。量测方程可以写为：

其中， H ∈R6×18是量测矩阵， v ∈R6是测量噪声。在使用两套INS的速度输出进行匹配时需要对FINS的速度杆臂误差进行补偿，修正后的FINS速度为：

在ARINS中，假设FINS解算得到的姿态没有误差，对应姿态阵；MINS实际解算得到的姿态存在误差，对应的姿态阵是。两个姿态阵可以分别表示为：

考虑到安装误差角µ，根据矩阵的链式乘法法则：

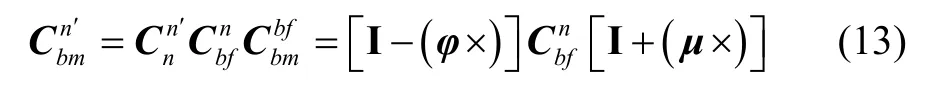
其中，φ和μ假设为小角度，将式(12)代入式(13)，MINS和FINS姿态阵元素间的对应关系有：

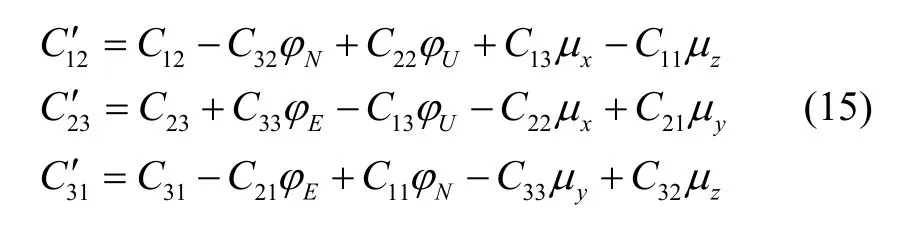
构造与姿态信息相关的量测方程：

其中，

2.2 变分贝叶斯Kalman滤波

为实现MINS的容错标定，有必要使用自适应滤波在线辨识模型中的未知时变量测噪声。变分贝叶斯方法可以逼近状态量和量测噪声的联合后验分布，以得到它们的次优估计。设离散化后，系统的状态空间模型如下：

式(21)中的积分运算通常是无法获得解析解的，为此对后验更新使用变分贝叶斯近似可以得到以上过程可实现的递推形式。要预测的联合后验概率分布可以表示为高斯分布和逆Gamma分布的乘积：

将观测噪声方差建立为启发式动态模型（heuristic dynamics model）：

其中，系数 ρ∈ (0,1]，通常可以选择为1-exp(-4)。则联合预测分布可以表示为式(25)。

根据式(22)-(25)，现在的后验更新步骤中，状态和量测噪声方差通过似然函数耦合，仍然无法得到准确的后验解析解。为了使式(25)计算易于处理，将对后验分布进行变分近似，可以得到如下分解形式的近似解：

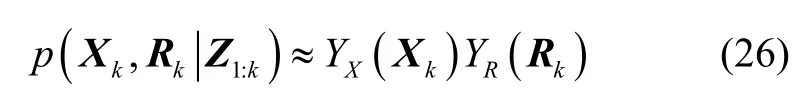
令分解后的近似分布式(26)与真实后验概率分布(25)之间的Kullback-Leibler散度最小。 YX（ Xk）服从高斯分布， YR（ Rk）服从逆Gamma分布：

量测噪声协方差可以表示为：

后验分布的结果可进一步表示为：

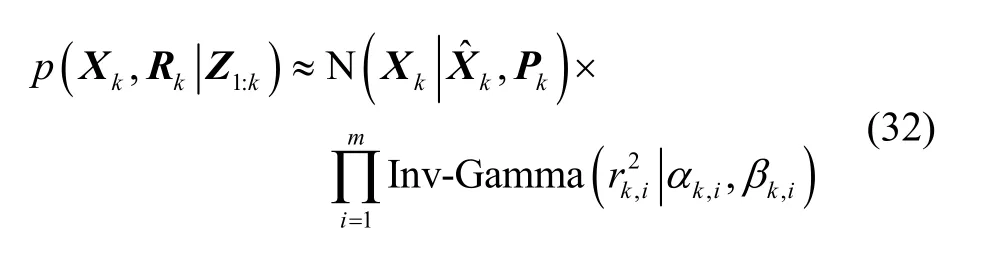
为了避免对高维矩阵的求逆运算，减小滤波算法的运行时间并增加算法的数值稳定性，对本节使用的变分贝叶斯自适应Kalman滤波进行序贯处理，改进后基于序贯结构的VB-AKF算法如算法1所示。提出的ARINS将使用该算法完成对MEMS-INS的动态标定。

算法1 基于序贯的变分贝叶斯Kalman滤波Algorithm 1 Variational Bayesian adaptive Kalman filter based on sequential structure

3 基于收敛度的估计结果量化评价与估计反馈策略

3.1 动态滤波收敛度的定义

状态向量的可观测性及可观测度分析中，通常使用分段线性定常系统（Piece Wise Constant System,PWCS）理论。然而这种方法只能在系统运行前以离线的方式进行理论分析，考虑到随机噪声的影响时，这种理论将不再严谨[15]。对此有学者针对导航系统存在随机噪声的特点，提出了较为严密的可观测性分析方法[16]，但是仍具有计算量大等缺点，不适合用这些方法评价状态变量的收敛性能。

在Kalman滤波中，矩阵Pk反应了各个状态之间的协方差，其中对角线元素代表了状态估计的误差。对于时变系统， Pk对角线元素随时间的变化可以定量地描述状态估计有效性的强度水平。为了在滤波时可以对状态变量估计的收敛程度有一个直观的认识，本文中使用 Pk与其初始化矩阵 P0对角线元素之比的算术平方根定义为收敛度。对于状态向量中的每一个变量（i ），其收敛度可以定义如下：

其中，n为状态变量的维数； οk∈Rn代表了k时刻的收敛度； P0是初始协方差矩阵，它反映了初始状态X0的估计误差。根据该定义，收敛度在每一个滤波时刻k都可以获得更新， οk（i）越大就意味着对应的状态变量可以获得更加精确和快速的估计。

3.2 基于收敛度的估计结果量化评价

需要注意的是，收敛度οk只是代表了对应状态量具有的可以被估计到的水平，并不意味着在某一个时刻k，状态量具有了很高的收敛度那么在这个时刻的对应状态量的估计结果就是完全准确的。所以式(33)得到的k时刻收敛度kο就不适合直接应用于对状态变量估计精度的评价。考虑对收敛度kο进行指数加权迭代，得到指数加权收敛度 kO：

其中，Ok-1为k-1时刻的指数加权收敛度，并且O0=0n×1；b定义为遗忘因子，通常的取值范围是0.95 ＜ b ＜ 0.99。无论收敛度有没有经过指数加权，它都没有具体的上界和下界，并且不同状态变量的估计结果可能对应不同数量级的收敛度，这就导致无法使用一种一致的、基于收敛度的标准对系统中每一个状态变量的估计进行评价。

为了得到状态估计的统一量化评价结果，考虑将式(34)中的指数加权收敛度 Ok通过映射函数进行转换。本文中建立的映射函数 T（ Ok）可以描述为：

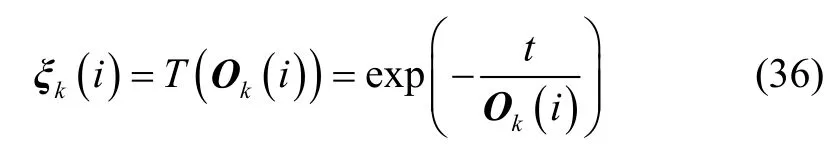
其中，ξk定义为状态量估计的归一化评价；t为映射变换参数，它的取值与本文为了判断估计结果是否满足要求而给定的判断评价标准S密切相关。图3展示了不同参数t下指数加权收敛度 kO与状态估计归一化评价ξk之间的关系。

图3 不同t值下的量化评价与指数加权收敛度之间的关系Fig.3 The relationship between Ok and ξk under different t

估计结果的量化评价通过指数加权操作后，将无界的收敛度通过函数 T（ Ok）映射到[0,1]区间内，把不同变量的评价标准统一为本文提出的估计归一化评价ξk，以此更加直观地判断估计精度的可信程度。

3.3 基于量化评价的估计反馈策略

基于状态估计的量化评价方法，本节提出一种估计反馈策略，以保证ARINS故障检测和导航输出的可靠性。如果其中待校正的MINS发生故障，那么该故障被诊断到后ARINS将直接使用FINS的输出，无法验证MINS的校正效果，因此本文将只聚焦于FINS的故障来完成对估计反馈策略的介绍。

由于MEMS惯性器件较低的性能，如果MINS中的误差参数没有利用估计结果进行补偿，那么MINS中的导航误差将会随时间急剧累积，使得式(3)(4)(5)变得非线性，并使基于线性化假设的VB-AKF估计过程发散。假设开始导航时刻为0，故障被检测到的时刻为Tf，那么时间段1就是导航开始到故障被检测到的这段时间[0, Tf)，时间段2就是[Tf,∞)。则基于估计量化评价的反馈策略（Estimation Feedback Strategy, EFS）可以描述为：

(1) 在时间段1，对MINS的姿态失准角、速度和位置误差（即导航误差）进行反馈，如图4(a)所示。

(2) 在故障被检测到的Tf时刻，除了反馈导航误差，还需要对状态变量中包含的MEMS器件误差完成量化评价后进行反馈。考虑为归一化评价指标引入一个评判标准 S，只有当对应的状态量Xˆi有ξk（i）＞S 时，该状态量的估计结果才是可信的。根据实际经验，评判标准S被选择为0.6826(1σ)。如图4(b)所示。

(3) 完成故障诊断与误差校正后（ t＞Tf），MINS将直接通过滤波一步预测过程得到的误差信息完成对导航信息的校正与输出，不使用FINS的姿态与速度对滤波一步预测结果进行修正，如图4(c)所示。

图4 估计反馈策略流程图Fig.4 The flowchart of estimation feedback strategy

4 仿真结果与分析

4.1 仿真参数设置

为了验证提出算法的有效性，本节使用仿真数据进行相关实验并对结果进行分析。对于本文设计的ARINS，两套惯导输出频率都为200Hz，惯性器件的误差参数如表1所示，两套惯导之间的安装误差角μ设为0°，由于它们在刚性基座上的安装位置较近，因此忽略杆臂带来的影响。VB-AKF的滤波周期为0.1 s，其中系数 ρ=1- exp （ -4 ），高斯-牛顿迭代次数N=5。故障检测的周期被设置为0.1 s。式(35)中，遗忘因子b=0.99。式(36)中，当评价标准S设置为0.6826时，映射参数t取5便是合适的。

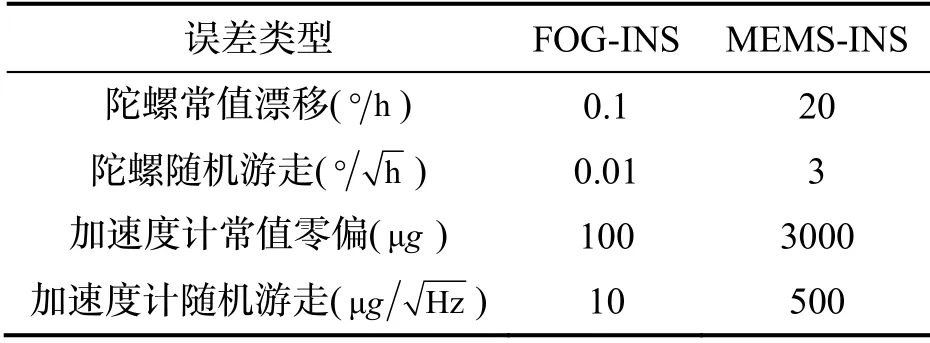
表1 器件误差参数Tab.1 IMU Device Error Parameters

在设置的675 s仿真轨迹中，初始位置对应纬度40 °、经度116 °，0~100 s车辆静止，之后的机动过程中包括了变速、转弯以及小动态范围（几度）的俯仰和横滚运动。故障情形可以描述为：给FINS的y轴陀螺在570~580 s人为加入0.2 rad/s（11.46 °/s）的软故障，完成故障诊断后，系统用经过校正的MINS输出载体的导航信息。

4.2 标定结果与量化评价

基于4.1节的相关设置，使用VB-AKF滤波残差的分段SPRT算法可以在延时0.8 s后检测到加入的故障，作为对照使用KF滤波残差的分段SPRT算法则在2.1 s后检测到加入的故障。在加入的故障被检测到以前，两种滤波算法对应的MEMS-INS y轴陀螺漂移、z轴陀螺漂移以及y轴加速度计零偏的标定结果如图5-7所示。

图5 MEMS陀螺常值漂移估计（y轴）Fig.5 Estimation of MEMS y-axis gyro drift

图6 MEMS陀螺常值漂移估计（z轴）Fig.6 Estimation of MEMS z-axis gyro drift

图7 MEMS加速度计常值零偏的估计（y轴）Fig.7 Estimation of MEMS accelerometer bias of y-axis

对于给定的MEMS惯性器件误差，在VB-AKF下y轴陀螺漂移、z轴陀螺漂移和y轴加速度计零偏的估计分别是：13.89 °/h、23.83 °/h和2928 µg，对应有估计误差30.55%、19.15%和2.40%；KF下对应误差参数的估计结果分别是：-11.82 °/h、31.88 °/h和2993 µg，对应有估计误差：159.10%、59.40%和0.23%，标定结果如表2所示。对于惯导性能影响最大的陀螺漂移，VB-AKF的估计精度相比于KF的估计分别提升了80.80%和67.76%。在系统存在故障时经过VB-AKF算法标定的MEMS器件误差参数的准确性明显高于KF算法的标定结果。

表2 MEMS惯性器件标定结果Tab.2 MEMS inertial device calibration results

同时根据3.2节设计的基于指数加权收敛度的估计结果量化评价算法，还可以得到基于VB-AKF的部分状态估计的量化评价如图8所示。

图8 各状态的量化评估结果Fig.8 Quantitative evaluation of corresponding states

对于本文的ARINS，VB-AKF和KF都无法对状态变量实现无偏估计。在故障检测算法存在延迟的时间内，KF的估计结果已经发生了明显发散，但是VB-AKF在这段时间内的估计结果并不会产生剧烈的变化，证明VB-AKF对于基准FINS中的故障具有良好的容错性能。因此，对于考虑基准系统存在故障可能性的在线标定过程中，由于故障检测不可避免的延时，自适应滤波算法是必不可少的。

MINS的动态标定模型是线性时变的，其状态变量的估计性能与载体的机动方式密切相关。在本节仿真实验设置的机动方式下，状态变量在故障发生前都可以获得较好的估计，明显高于给定的评价标准S。

4.4 基于估计反馈策略的误差校正

ARINS在完成故障诊断后，将只依靠MINS完成后续的惯性导航参数输出。根据4.3节的结果，使用KF发散的错误估计结果补偿MEMS器件误差必将增大MINS的系统误差，为此考虑以下两种对MEMS惯性器件误差的处理情况：（1）不补偿（2）故障情况下基于VB-AKF补偿。本节的结果都是以无故障时理想FINS的水平位置解算输出作为参考。

由于考虑的情况（1）中没有对MEMS的惯性器件误差进行任何补偿，此时的水平位置误差会随着时间而急剧累积；而情况（2）使用本文提出的VB-AKF和估计反馈策略对MEMS惯性器件的误差进行容错估计和补偿，可有效抑制后续导航过程中水平位置误差的发散。当故障在570 s发生后，60 s内（即570~630 s）这两种情况下的ARINS水平位置误差随时间变化的趋势如图9所示，其中630 s时未经过补偿的水平位置误差是173.30 m，经过补偿后水平位置误差为77.55 m，精度获得了55.25%的提升。

图9 基于VB-AKF和估计反馈策略补偿后的ARINS水平位置误差Fig.9 Horizontal position error of ARINS with compensation based on VB-AKF and EFS

再分别对考虑的两种情况进行10次仿真实验，得到630 s时水平位置误差如表3所示。相比于不补偿的情形，VB-AKF+EFS补偿后水平位置误差减小了33.59%，该结果进一步验证了提出方法的有效性。

表3 水平位置误差Tab.3 Horizontal Position Error

5 结 论

针对一种同时装备有FOG-INS和MEMS-INS的非对称冗余惯性导航系统，本文建立了MEMS-INS误差模型，使用变分贝叶斯自适应Kalman滤波进行在线容错标定并补偿导航误差，基于指数加权收敛度的估计精度量化评价算法可以直观地反馈MEMS惯性器件误差。仿真实验验证了提出算法的有效性。经过0.8 s的故障检测延迟，完成校正的MEMS-INS误差发散趋势得到明显抑制，与无器件估计误差反馈的过程相比，系统故障后60 s内水平位置精度提升了33.59%，使得冗余结构下系统在成本和体积受约束时也能够保证可靠的惯性导航参数输出。这些成果在特定组合导航应用场景下具有一定工程意义。