一种基于改进DTW的人体运动模式感知算法
2022-09-26闫国栋尹业成于志远乔尚岭
李 浩,闫国栋,尹业成,于志远,乔尚岭
(1. 北京精密机电控制设备研究所,北京 100076;2. 航天伺服驱动与传动技术实验室,北京 100076)
外骨骼机器人是一种智能可穿戴设备,目前已逐步应用于消防、医疗、工业等领域[1]。能否准确感知出穿戴者当前的运动模式,是外骨骼机器人实现人机协同功能的重要前提条件。目前常用于人体运动模式感知的算法包括支持向量机(Support Vector Machine,SVM)[2]、随机森林(Random Forest, RF)[3]、K近邻(K-Nearest Neighbor, KNN)[4]、卷积神经网络(Convolutional Neural Networks, CNN)[5]、长短时记忆神经网络(Long Short-Term Memory, LSTM)[6]等,上述基于机器学习或深度学习的算法通常需要大量含标注的训练集做为支撑、存在超参数最优解搜索困难等问题。动态时间规整(Dynamic time warping, DTW)算法最早由日本学者Itakura提出,目的是采用动态规整的思想衡量两个不同长度时间序列的相似程度[7],在语音识别[8],手势识别[9]等领域取得了广泛应用。与机器学习和深度学习相比,DTW算法无需进行特征提取等工作,可直接对传感器数据进行相似性匹配,当感知的运动模式种类发生变化时,只需增加或删减相应运动模式的模板,具有结构简单、模型易修正、可解释性强等优点。
传统DTW算法中的路径约束条件要求待测序列与标准模板间必须进行逐点匹配,可能会出现匹配路径偏离对角线较远、一个序列中的某个点与另一个序列中的连续多个点相匹配的情况。在一个完整的步态周期内,人体下肢运动具有波形相似,时间长度不固定的“准周期”特性,传统路径约束条件势必会影响最优匹配路径的可靠性,进而影响算法的精度。为降低算法的计算量和避免匹配路径过度偏离,目前最常用的方法是在原有的路径搜索区域的基础上,绘制一个平行四边形区域[10,11],一旦匹配路径触碰到绘制区域的边界,便通过修改路径约束条件的方式,将匹配路径限制在规定范围内。这种方法虽然可以对匹配路径进行一定范围的限制,降低一部分计算量,但仍然无法避免连续“一对多”现象对感知结果影响。
针对传统DTW算法存在的问题,本文首先提出了一种新的路径约束条件,并适当松弛算法的端点;然后在多传感器进行决策层融合时,设计了一种自适应权重分配机制;最后采集人体下肢的运动信息进行实验,对行走、上楼梯、下楼梯、跑步、上坡和下坡6种下肢外骨骼机器人常应用的运动模式进行感知。
1 算法流程
IMU因具有可穿戴性强、功耗低等优点,在人体运动模式感知领域得到广泛的应用,将IMU绑缚于人体下肢,可采集人体运动过程中产生的运动信号,如加速度、角速度等。本文设计的算法主要包括步态周期的划分、标准模板的构建和相似度的匹配三部分:首先对IMU采集的原始数据进行分割,获取一个完整的步态周期;然后离线构建一个步态周期内不同运动模式的标准模板;最后将改进后的DTW算法与自适应权重分配机制相结合,通过相似度匹配完成运动模式的感知。流程图如图1所示。

图1 人体运动模式感知算法流程图Fig.1 Flow chart of human movement pattern recognition algorithm
2 数据采集与预处理
2.1 数据采集
受身高、体重、自身运动习惯等因素的影响,人体运动模式具有显著的类间相似性和类内可变性,为了更好地获取运动信息,本文选择4个IMU,分别安装于左右大小腿外侧,采集运动过程中各IMU沿X轴的加速度与矢状面角速度(绕Z轴的角速度)。具体安装位置如图2所示。

图2 传感器安装位置示意图Fig.2 Schematic diagram of sensor installation position
2.2 数据预处理
在进行感知前,需要将IMU采集到的数据流形式的信号进行分割,以获取时间序列样本。人体下肢的运动通常具有周期性,本文根据步态周期的定义,通过小腿处IMU的矢状面角速度提取该侧足跟连续两次触地间的过程做为窗口,采用Savitzky-Golay滤波方法对窗口中的数据进行滤波,并将滤波后的数据进行归一化,以消除噪声和量纲差异的影响。
3 DTW算法的改进
假设两个不同长度的时间序列Q={q1, q2, q3…qM}和C={c1, c2, c3…cN}的长度分别为M和N,DTW算法需要构建一个矩阵元素为两序列各点间的欧式距离d(m, n)的时间规整矩阵DM×N,然后搜索使两序列间累加距离最小的最优匹配路径W,最后沿着最优匹配路径W对d(m, n)进行累加,便可得到两个时间序列的DTW距离D(M, N)。DTW距离越小,两个序列的相似度越高。

在寻找最优匹配路径W时,传统DTW算法要求必须满足以下三个路径约束条件:
(1) 边界性: w1=(1,1), wk=(M,N);
(2) 连续性:匹配过程中不得跳过两个序列中的任意一点;
(3) 单调性:匹配路径中的任意相邻两点必须满足:

该路径约束条件要求匹配时不得跳过两个序列中的任意一点,这可能导致序列Q中的某个点与序列C中的连续多个点或序列C中的某个点与序列Q中的连续多个点相匹配的情况,通过失真的匹配方式,强行降低两个相似度较低的序列的DTW距离。针对这一问题,本文提出一种允许跨点匹配的方法,将规整路径的斜率取值范围固定为0.5、1和2,求取最优路径的递归公式由传统算法中的式(4)变为式(5),改进后的DTW规整路径方向如图3所示。跨点匹配既可以保证匹配路径不会偏离对角线太远,也彻底避免了除端点外的“一对多”的现象。图4为同一组序列分别在传统路径约束条件下和本文提出的改进路径约束条件下的最优匹配路径,其中下方红色曲线为序列Q,右侧蓝色曲线为序列C,中间黑色曲线为当前路径约束条件下的最优匹配路径。从图中可以发现,在匹配过程中,当m和n均大于2时,对于同一组序列,改进后的算法避免了匹配过程中出现连续横向或纵向的失真现象,最优匹配路径更加光滑。
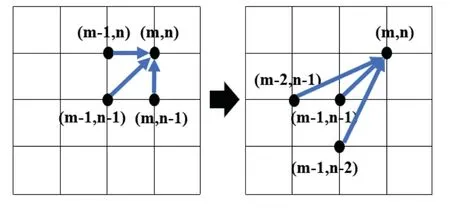
图3 DTW规整路径方向Fig.3 The direction of search path of DTW algorithm
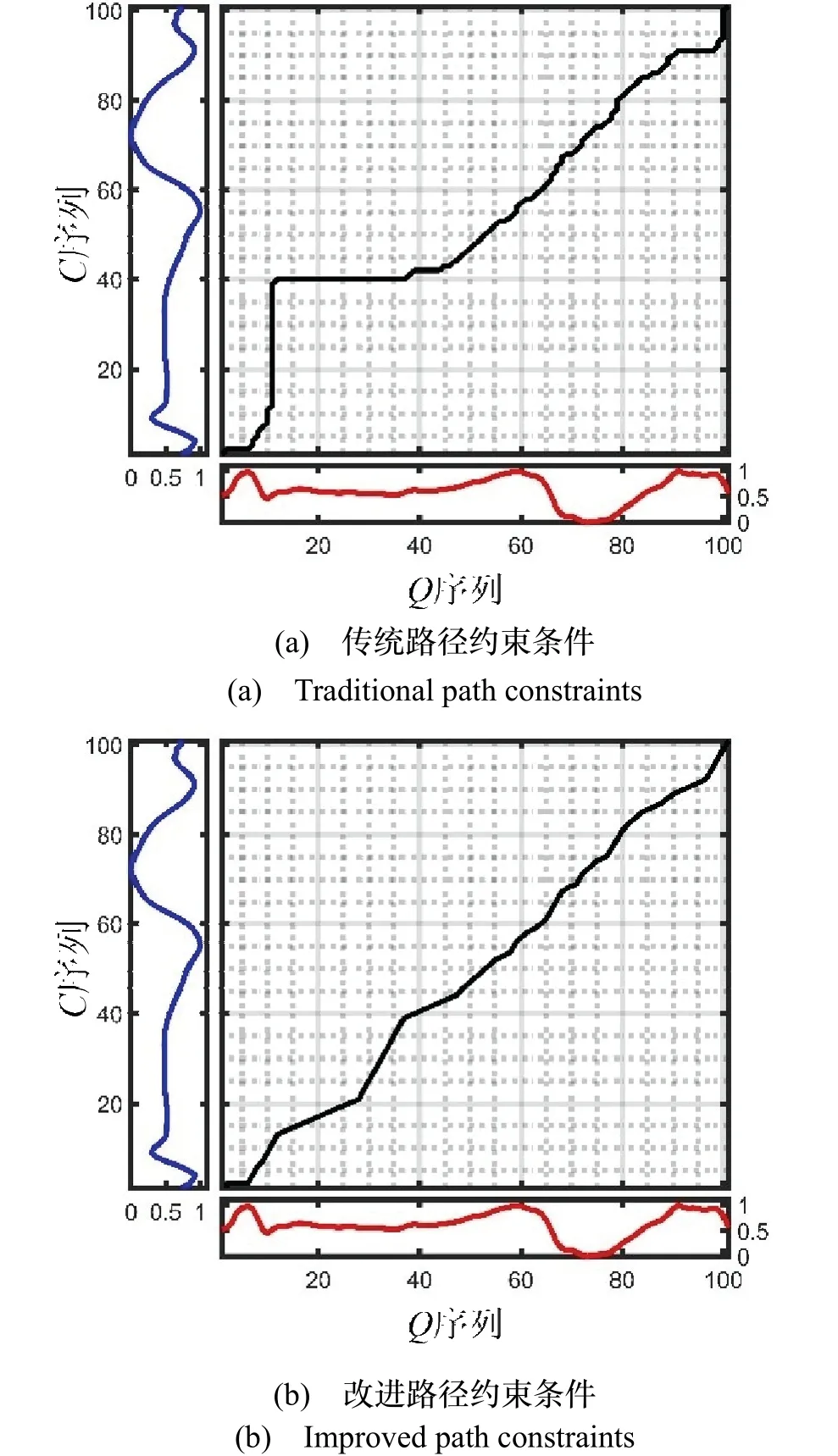
图4 最优匹配路径Fig.4 The best warping path
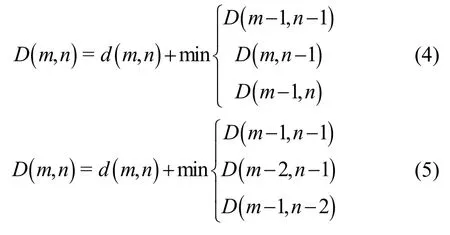
受步态周期提取算法的限制,待测样本无法保证能与标准模板的端点完全对齐。为解决这一问题,本文采用文献[10]中的方法,取消传统DTW路径约束中w1=(1, 1),wk=(M, N)的要求,通过设置松弛范围R和T,让DTW算法自主选择R和T中最小值对应的点做为算法的两个端点。

4 自适应权重分配机制
IMU的n轴数据分别选择各自DTW距离最小的标准模板对应的运动模式进行分类,通过多投票表决的方法,将各轴数据的分类结果进行决策层融合。由于各分类器的性能不同,各轴数据所得结果的可信度往往并不一致,在多投票表决中,若要给各分类器相同的投票权重,势必会对投票结果的精度产生影响。为解决这一问题,目前最常用的方法是事先获得各分类器性能的先验知识,根据先验知识分配投票权重,如D-S证据理论[12]等。然而分类器性能的先验知识通常需要大量实验才能获得,且因人而异。
考虑到DTW算法中相似程度可通过距离表示,本文设计了一种自适应权重分配机制:首先通过待测样本与各标准模板间的DTW距离确定各分类器的置信度,然后将总投票数n根据置信度进行自动分配。该机制不仅可以根据当前待测样本,自动调整各分类器的投票权重,而且无需各分类器性能的先验知识,具体流程如下:
step1计算IMU各轴数据xi与各标准模板之间的DTW距离,i=1...n,记录最小距离与次小距离Li1、Li2,选择Li1对应的运动模式为xi的感知结果Ai,得到各分类器感知结果的集合A,A={A1, A2, A3... An};
step2利用式(8)计算xi在权重分配中所占票数Vi:
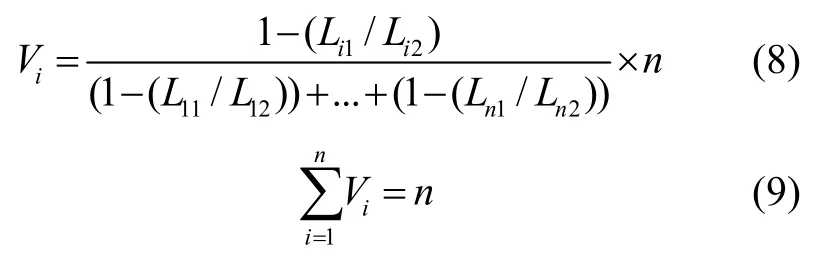
step3根据感知结果集合A和式(8)所得权重对各分类器的结果进行决策层融合,获得最终的感知结果。
需要指出的是,Vi与Li1/Li2成反比,Li1/Li2越小,数据xi与相似度最高的标准模板间的DTW距离越小于xi与其它标准模板的DTW距离,表明该感知结果的置信度越高,在决策层融合中所占的权重也应越高。
5 实验与分析
5.1 标准模板构建
为验证本文所提算法的可行性,共采集了14名测试人员的数据(男性10名,女性4名,年龄23岁~29 岁,身高162 cm~183 cm,体重52 kg~77 kg)。IMU型号为荷兰Xsens公司的Xsens MTw,如图5所示,采样频率为100 Hz,加速度量程为160 m/s2,角速度量程为2000 °/s,可自动实现多个IMU之间的时间同步。测试人员将IMU按照图2所示位置进行安装,数据采集过程中不对测试人员的行为习惯设置约束,采集顺序为行走-上楼梯-下楼梯-跑步-上坡-下坡。

图5 Xsens MTw传感器Fig.5 Xsens MTw sensor
实验采用标准民用楼梯(高16 cm宽27 cm),斜坡的坡度为8°,数据采集共得到4781个完整的步态周期,各运动模式的占比如表1所示。

表1 各运动模式的占比Tab.1 Proportion of each movement mode
我们随机选择了6名测试人员的数据,将样本通过采样或插值的方式对齐到相同长度,再进行平均以创建标准模板库,然后将另外8名测试人员的数据作为测试集进行测试。人体的左右腿在运动过程中具有对称性,图6-9显示了归一化后不同运动模式下左侧大小腿的标准模板曲线。可以看出,各运动模式之间具有一定的区分度。

图6 左侧大腿X轴加速度模板Fig.6 Template of X-axis acceleration of left thigh

图7 左侧大腿矢状面角速度模板Fig.7 Template of sagittal angular velocity of left thigh
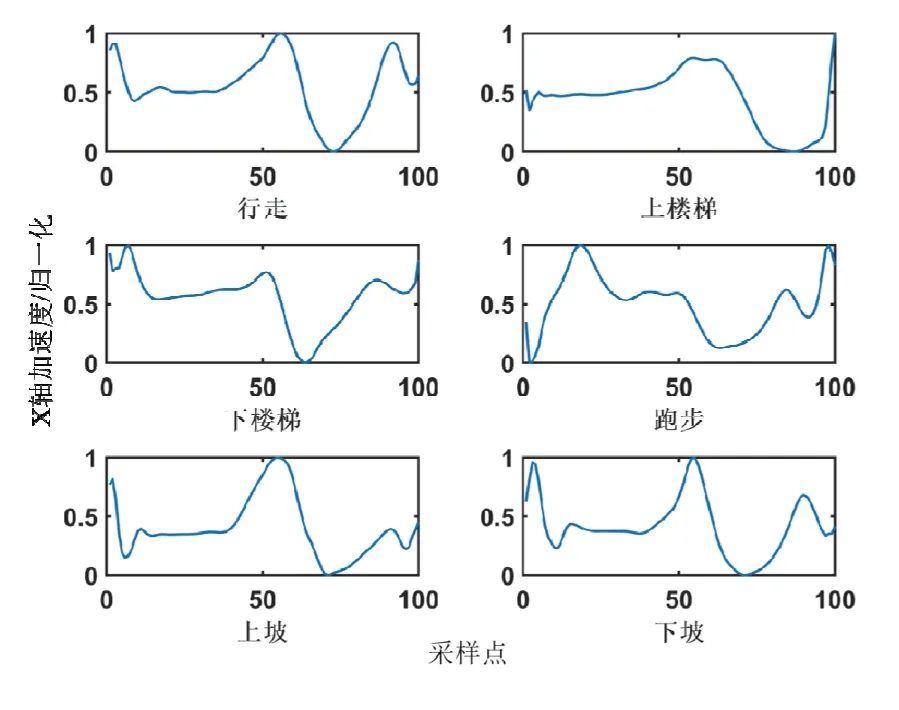
图8 左侧小腿X轴加速度模板Fig.8 Template of X-axis acceleration of left shank
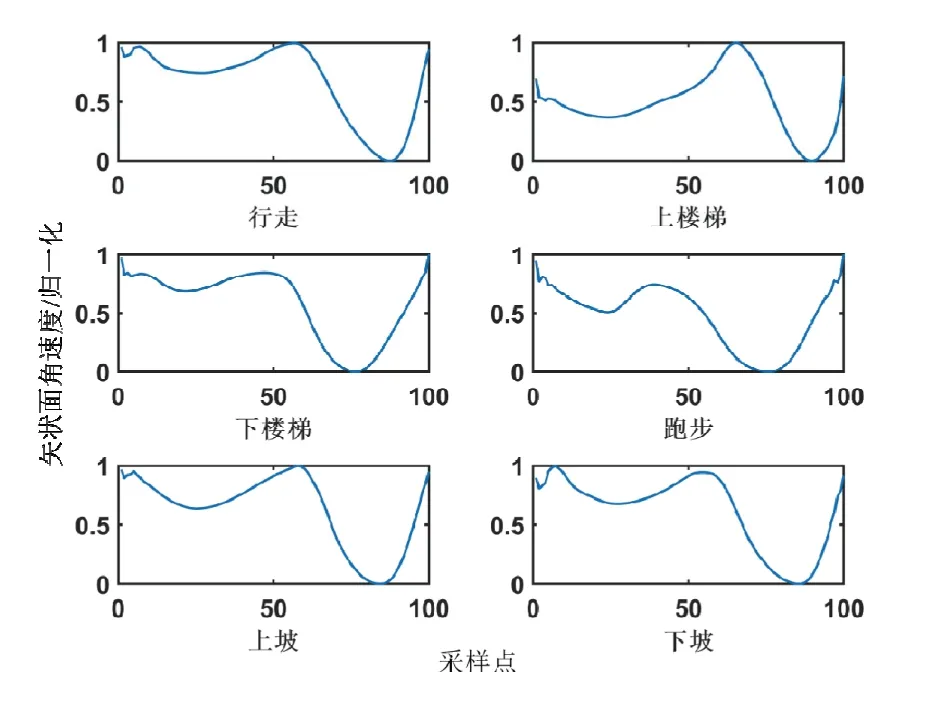
图9 左侧小腿矢状面角速度模板Fig.9 Template of sagittal angular velocity of left shank
5.2 改进DTW算法测试
采用传统DTW算法,搜索松弛范围S的最优解。由于端点部分数据无法对齐的现象只在很小范围内出现,参数S不宜过大,这里选择2~5,并与固定端点(S=1)进行对比,表2列举了设置不同松弛范围时的感知精度,当S=3时精度最高,为91.86%。

表2 不同松弛范围时的平均精度Tab.2 Average accuracy in different relaxation ranges
确定松弛范围S后,本文在各分类器具有相同投票权重的情况下,分别采用文献[10-11]的平行四边形搜索区域方法与本文提出的跨点匹配的方法进行实验。表3列举了不同方法下各运动模式的感知精度,其中平均精度为六种运动模式各自精度与从表1中筛选的8名测试人员样本数所占权重相乘后累加的结果,依次为94.08%和96.09%。
从表3中可以看出,当使用传统DTW算法时,只有上楼梯和跑步两种运动模式取得了较好的感知结果,其余四种运动模式的误判概率均较高。设置平行四边形搜索区域虽然可以将匹配路径限制在较为合理的范围内,在一定程度上提升感知结果的平均精度,但仍然无法避免“一对多”现象的影响。本文提出的跨点匹配方法可以同时解决以上两个问题,与设置平行四边形搜索区域的方法相比,除下楼梯的感知精度略有降低外,其余5种运动模式均有明显提升,证明了跨点匹配的优越性。
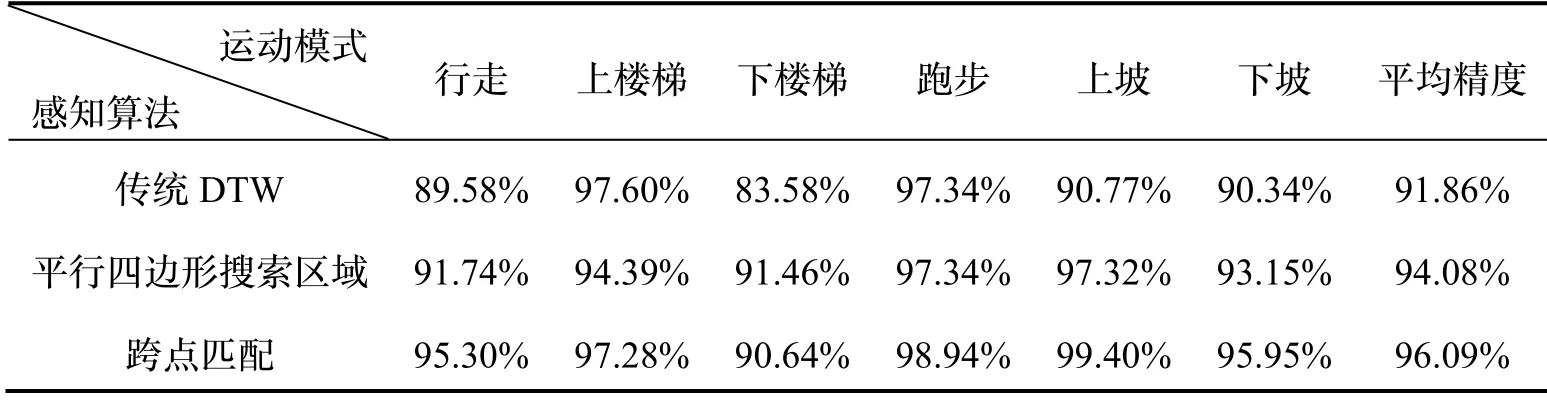
表3 不同感知算法下各运动模式的感知精度Tab.3 Recognition accuracy of each movement mode under different recognition algorithms
5.3 自适应权重分配机制测试
本文从混淆矩阵和实现正确感知时各运动模式的平均得票数两个层面对自适应权重分配机制的优越性进行验证。
图10 分别为将改进的DTW算法与自适应权重分配机制相结合前后的混淆矩阵。可以看出,引入自适应权重分配机制后,除行走和上坡的精度保持不变外,其余四种运动模式均有所提高。六种运动模式平均精度由96.09%提升到了97.64%。以下楼梯为例,引入自适应权重机制前,传感器各轴数据均具有相同的投票权重,存在大量将下楼梯误判为行走的情况。引入自适应权重分配机制后,下楼梯的平均精度从原来的90.64%提升到了97.21%,表4为下楼梯时各轴数据的投票权重平均值和投票数平均值,由表4可知,各轴数据在决策层融合时能够根据当前感知结果的置信度,自动调整分类器的投票权重。此外,图11对比了将改进的DTW算法与自适应权重分配机制相结合前后,各运动模式在实现正确感知时的平均得票数。可以看出,自适应权重分配机制下的各运动模式的平均得票数明显高于相同投票权重的方法,进一步证明了该机制的优越性。
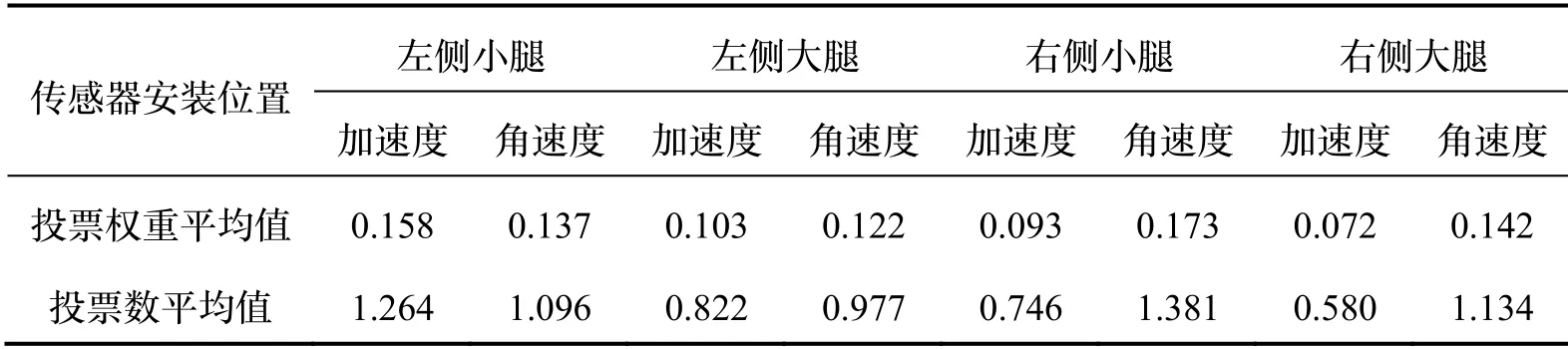
表4 引入权重分配机制后下楼梯时的投票权重分配情况Tab.4 Voting weight distribution when downstairs after the introduction of the weight allocation mechanism

图10 混淆矩阵Fig.10 Confusion matrix

图11 正确感知时各运动模式的平均得票数Fig.11 The average number of votes of each movement mode in correct recognition
6 结 论
本文首先针对传统DTW算法存在的问题,提出采用跨点匹配、适当松弛算法端点的方法对DTW进行改进;然后在多传感器决策层融合中引入了一种基于置信度的自适应权重分配机制;最后通过实验进行验证。实验结果表明,在各分类器具有相同投票权重的融合方式下,改进的DTW算法较传统算法的平均精度提升了5.31%,达到96.09%;引入自适应权重分配机制后,平均精度进一步提升了1.55%,达到97.64%,验证了本文所提出的改进DTW算法和自适应权重分配机制的有效性。
