含冲击损伤复合材料层合板疲劳寿命预测
2022-09-26刘俭辉薛文卓
刘俭辉, 薛文卓, 魏 泰
(1.兰州理工大学 机电工程学院, 甘肃 兰州 730050;2.甘肃省特种设备检验检测研究院 风电设备质检中心, 甘肃 兰州 730050)
纤维增强复合材料具有比强度高、比刚度高、可设计性强和耐疲劳性能好等优点,在新能源行业、航空航天和汽车领域得到广泛应用[1-3]。然而,复合材料层合板在制造、运输和使用过程中难免会遭受各种损伤,其中冲击损伤尤为突出。目前,风力发电机叶片的材质多为复合材料,由于其服役过程中会遭受飞鸟、沙石等冲击,这类低能量冲击会对叶片内部产生冲击损伤,但在表面不易被发现,这会严重影响风电叶片在服役过程中的安全性和使用寿命[4-7]。当层合板受到低速冲击产生不可视的损伤后,会导致复合材料层合板的剩余强度和疲劳性能显著下降[8-9]。因此,开展含冲击损伤的复合材料层合板疲劳寿命研究很有必要。
目前,Shreyas等[10]研究了不同低速能量冲击后复合材料层合板的拉-拉疲劳行为,发现冲击损伤对层合板的疲劳寿命有显著影响。Zhang等[11]分别研究了低速冲击和静态压痕对复合材料层合板疲劳寿命的影响。Beheshty等[12, 13]通过试验研究,使用等寿命曲线法预测了含冲击损伤复合材料层合板的剩余疲劳寿命。Kang等[14]利用剩余强度模型,对低速冲击后的复合材料层合板进行强度折减,并预测了层合板的疲劳寿命。Koo等[15, 16]利用冲击损伤区域的特征长度,预测了C型结构碳纤维复合材料层合板的疲劳寿命。崔海坡等[17, 18]研究了不同的复合材料体系、几何尺寸、纤维铺设方式等工艺参数对碳纤维假脚的冲击损伤及疲劳性能的影响规律。邵洪[19]利用有限元模型,对复合材料层合板遭受低速冲击和冲击后的疲劳损伤过程进行模拟。
上述研究主要以试验为主,对于层合板冲击后的疲劳寿命预测,部分学者是通过有限元模拟得到,其建模和模拟过程比较复杂。而应力场强分析方法对含缺口层合板的强度预测效果较好。为考虑疲劳破坏对低速冲击后层合板剩余强度的影响,本文参考金属缺口件寿命预测模型,对含缺口的复合材料层合板的应力场强法进行修正。将低速冲击后的复合材料层合板等效为含孔层合板,基于无损伤层合板的指数函数疲劳寿命模型,建立了含低速冲击损伤的复合材料层合板疲劳寿命预测模型。用文献中收集的含冲击损伤复合材料层合板的疲劳试验数据,验证了本文预测方法的可行性。
1 含冲击损伤复合材料疲劳模型
1.1 含圆孔层合板剩余强度估算模型
1.1.1应力场强法
应力场强法[20](见图1)认为,存在应力集中的构件的破坏是由应力集中区的应力应变场造成的,构件的缺口强度应与缺口附近的应力应变场有关。应力场强法考虑缺口根部损伤区域内应力梯度的影响,通过引入权函数对场强区域内所有材料点的应力矢量进行分配,考虑不同材料点的应力对缺口根部失效的综合贡献。
缺口场强函数fRD的表达式如下:
(1)
式中:D为场强区域;s为D的面积;φ(r)为权函数;当fRD=1时,层合板发生破坏;f(σ)为曲面破坏函数,对于单层板,f(σ)可取Tsai-Hill多项式,对于层合板,确定层合板的各方向强度值后,f(σ)仍可近似取为Tsai-Hill多项式,具体表达式如下:
(2)
式中:X、Y和S分别为复合材料的纵向、横向和剪切强度。
式(1)可按照图2[21]所示求积分:
所以式(1)可改写为:
(3)
式中:R为缺口半径;L为y=0面的场径长度;θ为场强区域到x轴的最大偏角。
根据积分中值定理,式(3)可改写为:
(4)
式中:ds为特征长度;φ(x)为权函数。因为在y=0面上,可得f(σ)=σy(x,0)/σ0,其中σ0为y轴方向无损层合板的强度。
1.1.2孔边应力分布
将复合材料层合板等效为正交各向异性板来处理,对开圆孔无限宽板采用Nuismer-Whitney平均强度准则,得到正交各向异性复合材料层合板沿y轴加载方向的应力分布:
(5)
(6)
由于式(5)是由无限宽板得到的应力分布,所以需要对式(5)的预测强度进行修正,有限宽度修正系数[22]如下:
(7)
1.1.3权函数
权函数φ(x)表示y=0截面上距离圆孔根部x处应力对圆孔发生破坏的贡献。权函数应该满足下述几个基本条件[20]:
1) 0≤φ(x)≤1且φ(x)关于x广义单调递减;
2)φ(0)=1;
3) 当KT=1时,φ(x)≡1。
吴义韬等[21]根据权函数条件构造的权函数为:
(8)
式中:W为板宽;R为孔径。
针对临界距离法和权函数的限制条件,考虑后续疲劳破坏的影响,本文引入王昊元等[23]在金属缺口件疲劳寿命预测模型中提出的权函数,结合有限宽度的含孔层合板,得到修正后的权函数:
(9)
本文通过对杨洁等[24]预制的含孔层合板进行研究(R=2.5 cm,W=40 cm),得出权函数大小与缺口距离的关系,如图3所示。
由图3可知,两种权函数的整体趋势均为单调递减,且在KT=1时恒等于1。但是本文提出的权函数更符合孔边应力的递减规律[24]。
将式(7)代入式(5)得到修正后的含孔层合板的应力分布,结合权函数式(9),共同代入式(4),化简后即可得到含中心圆孔层合板的缺口强度表达式:
(10)
1.2 含冲击损伤层合板疲劳寿命模型
试验研究[25, 26]发现,含冲击损伤层合板的疲劳损伤扩展规律和开孔层合板类似;试验研究[27]还发现,两种层合板静强度的失效模式相似。因而可以将含冲击损伤层合板等效为相应孔径的开孔层合板。冲击损伤区域近似为圆形,损伤直径即等效开孔直径。
基于无孔层合板疲劳模型的指数函数规律,将层合板的静强度问题与交变动载荷疲劳行为联系起来:
(11)
式中:C、S为拟合常数;σmax为疲劳加载的最大应力;σS为复合材料层合板失效破坏的静强度;N为循环加载次数。
结合式(9)与式(10),即可得到含冲击损伤层合板的疲劳寿命预测模型:
(12)
2 模型验证
2.1 含冲击损伤层合板压-压疲劳
2.1.1试验
梁小林[27]预制了T300/5405双马酰亚胺复合材料层合板,单层板厚度为0.119mm,铺层为[45/45/0/-45/45/0/90/-45/0/45/90/0]s,共计24层,最终制成尺寸为200mm×80mm的试件进行冲击后压缩和疲劳试验。T300/5405试件的材料属性如表1所示。
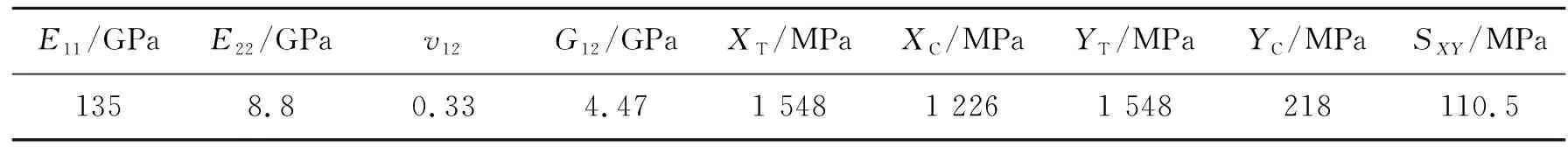
表1 T300/5405层合板的基本力学性能
对T300/5405双马酰亚胺复合材料层合板分别进行了12.55J和18.99J的低速冲击试验,通过超声C扫描设备对不同冲击能量的层合板进行损伤检测。冲击能量为12.55J时,试件的平均损伤面积和损伤宽度分别为565.56mm2、27.01mm;冲击能量为18.99J时,试件的平均损伤面积和损伤宽度分别为789.01mm2、30.30mm,损伤区域接近于圆形。对部分冲击后层合板进行剩余压缩试验,测得无损和含冲击损伤层合板的剩余压缩强度,如表2所示。

表2 冲击后层合板的剩余压缩强度
对承受不同冲击能量的复合材料层合板进行压-压疲劳试验,载荷波形为等幅正弦波,应力比为0.1,加载频率3~4 Hz,所有试验在常温下完成。
将冲击能量相同的层合板各分为5组:选取12.55J冲击能量下平均剩余压缩强度的60%、65%、70%、75%、80%为应力水平,选取18.99J冲击能量下平均剩余压缩强度的65%、68%、70%、75%、80%为应力水平进行疲劳试验,层合板冲击后的压-压疲劳寿命如图4所示。
2.1.2压-压疲劳寿命预测模型
使用最小二乘法对12.55J冲击能量的疲劳数据进行曲线拟合,得到低速冲击后层合板的指数函数规律的疲劳模型:
将含冲击损伤层合板等效为开孔层合板时,可用开孔层合板的特征长度a0代替含冲击损伤层合板的特征长度值。陈普会[28]的研究表明,开孔层合板的特征长度值为材料常数,其在拉伸和压缩情况下的取值不同,与铺层形式和缺口形状无关,需要根据试验来确定。根据试验得到18.99J冲击能量下层合板a0=5.959。
2.1.3模型验证
将计算结果代入预测模型,得到寿命预测值,并与试验结果进行对比,如表3所示。
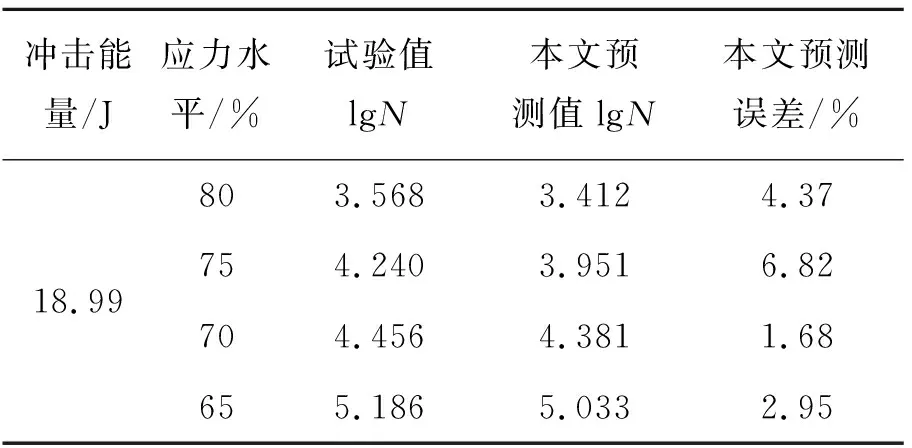
表3 冲击后层合板的压-压疲劳寿命预测及误差
2.2 含冲击损伤层合板拉-拉疲劳
2.2.1试验
徐颖[29]预制了不同铺层的T300/BMP316复合材料层合板,A、B试件的铺层角度分别为[45/-45/90/90/-45/0/45/90/90/0]s、[45/-45/90/0/-45/0/45/0/90/0]s,两种层合板均为20层,最终制成尺寸为200mm×40mm的试件进行冲击后拉伸和疲劳试验。T300/BMP316试件的材料属性如表4所示。
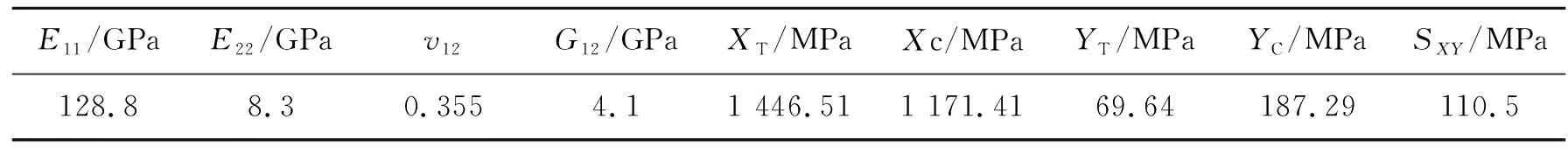
表4 T300/BMP316层合板的基本力学性能
通过试验测得A试件在两种冲击能量(5.9 J、8.6 J)下的损伤区域,并取部分冲击后试件进行静拉伸试验,如表5所示。

表5 冲击后层合板A的损伤面积及剩余拉伸强度
需要说明的是,原文中并未测得A试件(无损)的静拉伸强度,为获得该层合板的静拉伸强度,利用B试件的试验值进行类推,如表6所示。
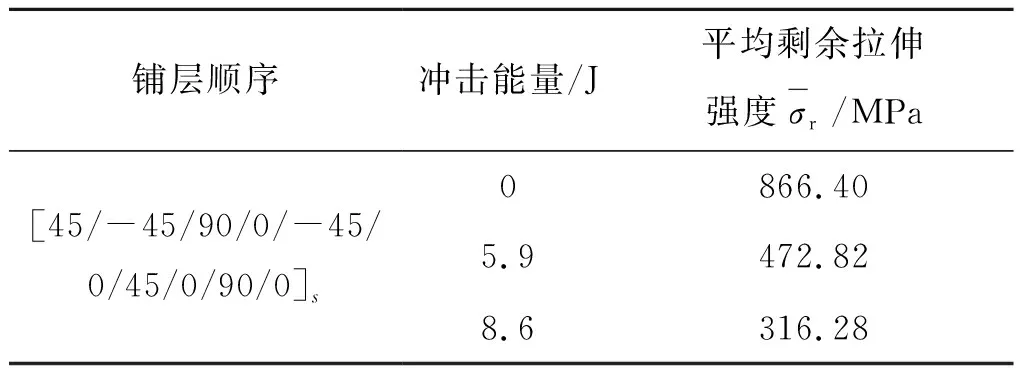
表6 冲击后层合板B的剩余拉伸强度
从铺层顺序来看,A试件0°铺层占总体铺层的20%,90°铺层占总体铺层的40%,而B试件的0°和90°铺层分别占总体铺层的40%和20%。试验表明,对于静拉伸强度,更多比例的0°铺层会带来更好的抗拉伸强度,通过试验数据可知,在5.9 J和8.6 J的冲击能量下,B试件比A试件的剩余拉伸强度分别提高16.8%和31.1%,因此可以近似得出A试件的无损静拉伸强度为757.34 MPa。
对承受不同冲击能量的复合材料层合板进行拉-拉疲劳试验,载荷波形为等幅正弦波,应力比为0.1,加载频率5~6 Hz,所有试验在常温下完成。
选取5.9J冲击能量下剩余静拉伸强度的90%、85%、80%、75%为应力水平,选取8.6J冲击能量下剩余静拉伸强度的80%为应力水平进行疲劳试验,层合板冲击后的拉-拉疲劳寿命如表7所示。

表7 冲击后层合板的拉-拉疲劳寿命[29]
2.2.2拉-拉疲劳寿命预测模型及验证
采用5.9J冲击能量的疲劳数据进行曲线拟合,得到疲劳寿命预测模型:
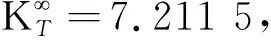
冲击能量在8.6J时,层合板在80%应力水平下的疲劳寿命预测值及误差,如表8所示。

表8 冲击后层合板的拉-拉疲劳寿命预测及误差
3 讨论与分析
对于复合材料层合板而言,层板中0°和90°铺层所占的比例会对其静强度造成影响,在拉伸试验中,0°铺层所占比例越大,层板的抗拉强度和拉-拉疲劳寿命越好。对于同一种层板,一般拉伸强度要高于压缩强度,具体表现在同一层板对拉伸和压缩所取的特征长度不同,而陈普会[28]的试验结果也印证了这一点。
引入文献[27]、[29]中复合材料层合板冲击后的压-压疲劳和拉-拉疲劳试验结果及预测误差,并与本文提出的疲劳寿命预测模型进行对比,结果如表9和图5所示。
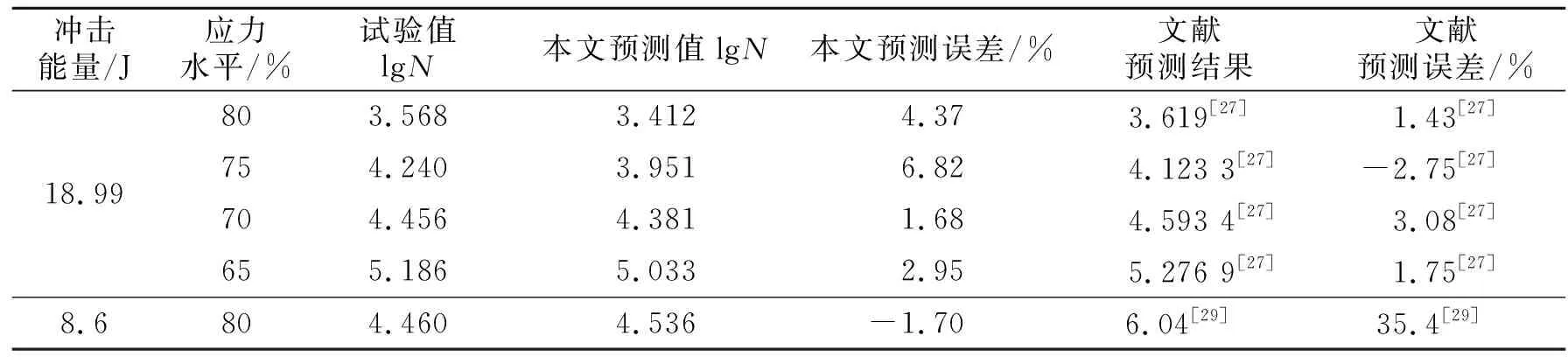
表9 冲击后层合板的疲劳寿命预测及误差分析
由表9可以看出,在不同应力水平的疲劳载荷下,本文提出的模型不仅适用于冲击后压-压疲劳寿命预测,对于冲击后拉-拉疲劳寿命预测也同样适用。与试验结果相比,误差最大为6.82%,误差最小仅为1.68%。尤其是对于冲击后层合板的拉-拉疲劳寿命预测,其预测精度显著提高。
4 结 论
1) 本文分析了孔边应力的递减规律,考虑了后续疲劳破坏对层合板寿命的影响,引入权函数作为孔边不同位置应力对损伤参量的权重,对复合材料含孔层合板的应力场强法进行修正。通过开孔等效法并结合无损伤层合板的疲劳寿命模型,建立了含冲击损伤的复合材料层合板疲劳寿命预测模型。
2) 通过现有试验数据,计算开孔等效法下冲击后层合板的剩余强度,分别建立了冲击后层合板的压-压疲劳和拉-拉疲劳寿命预测模型,并将预测结果与试验结果进行对比。结果表明:本文提出的寿命预测模型可以较为准确地预测含低速冲击损伤的层合板的疲劳寿命,误差在10%以内。
