无限板孔边裂纹问题的高精度解析权函数解

2018-09-29赵晓辰吴学仁童第华徐武陈勃胡本润

航空学报 2018年9期

赵晓辰，吴学仁, *，童第华，徐武，陈勃，胡本润

1. 中国航发北京航空材料研究院，北京 100095 2. 上海交通大学航空航天学院，上海 200240

无限板中的圆孔边径向裂纹是工程实际中常见的一类裂纹几何，该裂纹问题的求解方法在航空航天、机械运载、土木建筑、油气开采等工业领域中有非常广泛的需求。孔边裂纹在各种复杂载荷下的高精度应力强度因子(SIF)K和裂纹面张开位移(COD)等关键断裂力学参量，是计算和预测含孔边裂纹结构的疲劳寿命和剩余强度的重要前提[1]。虽然有限元法(Finite Element Method，FEM)和边界元法(Boundary Element Method，BEM)等数值方法能求解各种复杂载荷情况下的孔边裂纹问题，但数值方法对计算资源和使用者的经验均有颇高的要求。特别是在需要求解裂纹长度变化不断和(或)多种复杂载荷情况的裂纹问题时，数值方法的计算和校验工作量都很大，经济性较差。因此，寻求高效准确的孔边裂纹问题求解方法有重要的实际意义。

权函数法(WFM)是求解裂纹问题的一种高效手段[2-6]。它把影响应力强度因子的变量——裂纹体的几何(包括载荷/位移边界划分)和所承受的载荷作了分离。权函数仅与裂纹几何及载荷/位移边界(ST/SU)的划分相关，一旦确定，则仅需通过对权函数和假想裂纹处应力分布的乘积作简单积分就能够得到作为裂纹长度的函数的K和COD。因此在处理复杂载荷情况或同一裂纹几何多种载荷情况的裂纹问题，或对许多裂纹长度(例如疲劳裂纹扩展)求解时，权函数法可以在极大地提高计算效率的同时，保证结果的高精度。

权函数法总体上可以分为解析法和数值法2种。在解析权函数法方面，目前主要有：①Wu-Carlsson基于一种参考载荷下的K和CMOD参考解的权函数[4]；②Fett-Munz[5]、Glinka-Shen[6]分别发展的基于多种(一般为2种)参考载荷下的K求得的权函数。Wu-Carlsson解析权函数法能够直接得到作为裂纹长度α连续函数形式的权函数，不但能方便地求解连续变化α的K和COD，而且所得权函数受参考载荷形式及参考解精度的影响很小[7-8]，在现有解析权函数法中，其求解精度和鲁棒性均具有明显优势。在数值权函数方面，除了采用传统有限元法求解权函数外，Wagner-Millwater[9]近年来提出了一种基于复变函数泰勒级数展开的权函数(Weight function Complex Taylor Series Expansion，WCTSE)法。这种方法基于复变函数的泰勒级数展开理论，结合复变有限元计算，能够得到任意裂纹体几何的宽α范围离散裂纹长度的数值形式权函数。Jing和Wu[10]通过对WCTSE法的深入研究，进一步提高了其求解精度。在对复变有限元及裂纹问题建模方面积累了丰富经验的前提下，WCTSE法所求得的数值权函数具有很高的精度[7-8, 11]。但由于WCTSE法本质上是一种数值方法，对每个裂纹尺寸都需要进行一次复变有限元计算，因此其求解效率远低于解析权函数法。而WCTSE法的高精度特点，则使得它在对通过其他方法得到的权函数的精度评价验证方面具有独特的优势，因此可以作为评价解析权函数精度的“基准”。

本文利用Wu-Carlsson解析权函数法求得了无限板孔边单裂纹(N=1)和对称双裂纹(N=2)的权函数；并通过与权函数直接对应的格林函数(Green’s Function，GF)，分别与Shivakumar-Forman[12]和Newman[13]的高精度拟合表达式以及WCTSE数值权函数结果作了全面对比验证。此外，还指出了近期文献中的孔边裂纹权函数[14-15]的明显错误。在此基础上用得到的解析权函数公式计算了孔边裂纹在多种典型载荷作用下的应力强度因子，为复杂受载的孔边裂纹问题提供了形式统一、便捷高效的高精度求解手段。

1 无限板孔边裂纹的解析权函数

考虑无限板圆孔边的径向裂纹问题，即单裂纹(N=1)和对称双裂纹(N=2)，如图1所示。

根据权函数理论[2-6]，对权函数m(α,γ)和无裂纹体在假想裂纹处的应力分布σ(ξ)的乘积沿裂纹长度作积分，即可得到任意载荷条件下的应力强度因子为

(1a)

(1b)

式中：α=a/W,ξ=x/W,γ=ξ/α,a和x分别为裂纹的长度和坐标；W为裂纹体的特征尺寸；σ(ξ)为无裂纹体在假想裂纹处的应力分布；σ0为σ(ξ)的归一因子。对于无限板孔边裂纹，取孔的半径作为特征尺寸，即W=R，相关参量定义见图1。这里采用Wu-Carlsson解析权函数法对孔边裂纹问题进行分析。作为一种边缘裂纹，孔边裂纹的Wu-Carlsson权函数形式为[4]

(2)

(3)

式(2)表明，βi(α)是确定权函数m(α,γ)的前提，而βi(α)又由函数Fi(α)确定。所以Fi(α)的推导成为Wu-Carlsson权函数的关键环节。根据文献[4]，确定边缘裂纹Fi(α)的条件一般可包括：① 裂纹尖端的COD-K关系；② 参考载荷情况的K的自洽条件；③ 参考载荷作用下的裂纹嘴张开位移(CMOD)。Wu-Carlsson利用条件①和条件②在其权函数专著中给出了孔边裂纹的解析权函数[4]，并进而求解得到各种复杂载荷情况下的孔边裂纹应力强度因子[4, 16]。多位学者基于这2个条件，成功应用Wu-Carlsson权函数方法求解了各种孔边裂纹问题。近年来的典型例子有：有限宽板圆孔边单/双裂纹分析以及对参考应力强度因子拟合方法的改进[17]、无限板孔边不等长双裂纹的混合型问题的KI和KII以及裂纹张开位移[18]、周期性孔边共线裂纹的K和COD[19]。

本文研究发现，增加条件③能明显提高α较小时的求解精度。值得注意的是，裂纹面位移曲线在裂纹嘴处的曲率为0同样适用于边缘裂纹，但对多连域裂纹问题，此条件对精度的影响很小，且会增加求解的复杂性。这里采用条件①、条件②和条件③推导孔边裂纹的解析权函数。推导Fi(α)所需前提为：同一种参考载荷下的无量纲应力强度因子fr(α)和裂纹嘴张开位移Vr(α)的解。

以裂纹面均布应力(σ(ξ)/σ0=1)作为参考载荷，则有

F1(α)=4fr(α)

(4a)

(4b)

(4c)

式中：

(5)

(6)

(7)

为避免影响后续积分计算，将Φ(α)中的变量α替换为s；ρn和τn分别为fr和Vr的拟合多项式系数。考虑到当无量纲裂纹长度α>2.0时，孔对裂尖K的影响很小，此时可把孔视为裂纹长度的一部分作为无限板中心裂纹问题处理。因此本文仅考虑α≤2.0范围的解析权函数。α=0时，边缘裂纹的无量纲应力强度因子和裂纹嘴张开位移有精确解，分别为[20]：fr(0)=1.121 5，Vr(0)=2.908 6。用有限元法计算在裂纹面均布载荷作用下，α=0.1～3.0范围内多个裂纹长度的K和CMOD，结合α=0的精确解进行拟合，得到式(6)中fr(α)和式(7)中Vr(α)的多项式系数(如表1所示)，且多项式的最大拟合误差约为0.1%。

由式(6)可计算出式(5)，然后将式(5)～式(7)代入式(4)求得Fi(α)，进而由式(3)确定系数βi(α)，再由式(2)便能求得无限板孔边裂纹(N=1，2)的解析权函数m(α,γ)。表2给出了部分裂纹长度的βi(α)值。

为方便工程应用，对由式(3)计算得到的βi(α)值用式(8)作拟合：

(8)

式中:多项式系数bin在表3中给出。

以上多项式的拟合误差，除βi→0的局部区域外，均不超过1.0%；用式(8)计算的格林函数与式(3)相比，偏差不超过0.3%。

表1 无限板孔边裂纹无量纲应力强度因子和裂纹嘴张开位移的多项式系数Table 1 Fitted coefficients of dimensionless SIFs and CMODs for radial crack(s) at circular hole in infinite plate

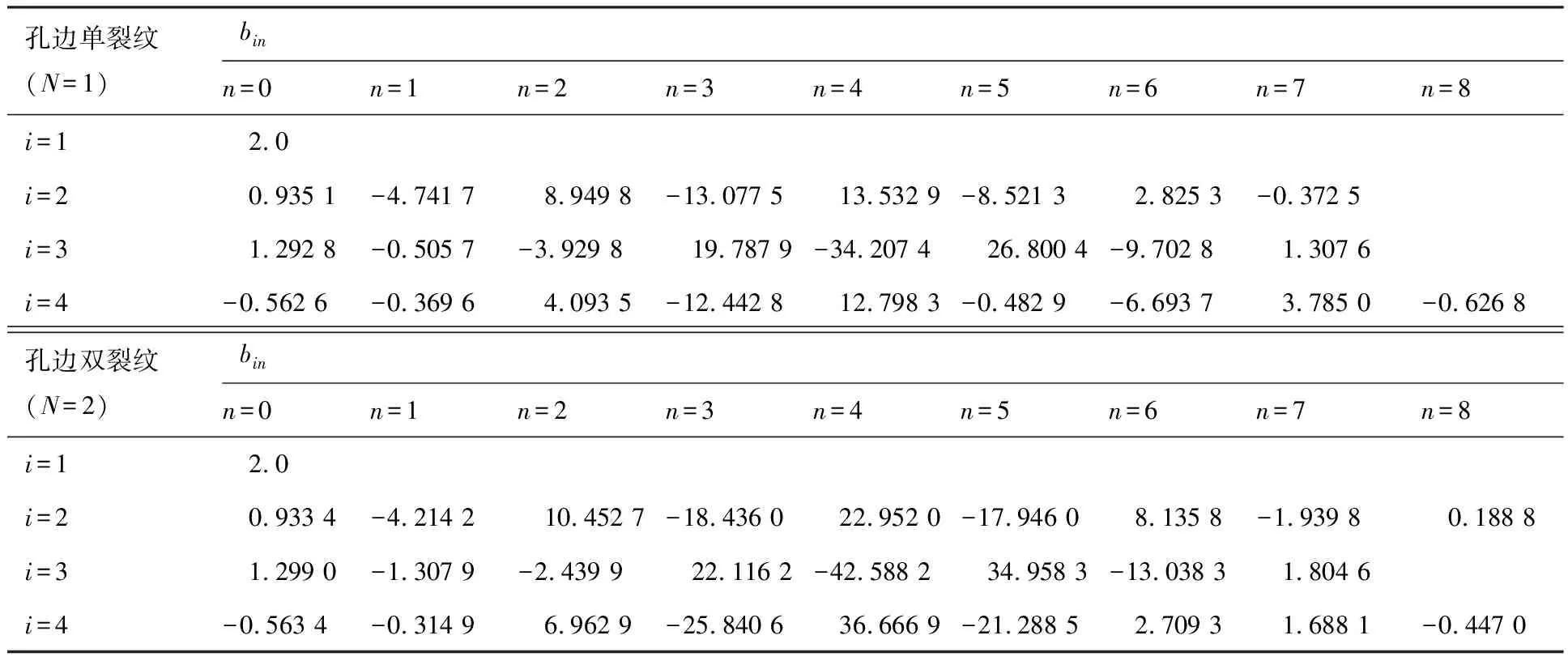
表3 无限板孔边裂纹解析权函数系数βi(α)的拟合多项式系数Table 3 Fitted polynomial coefficients for βi(α) of radial crack(s) at circular hole in infinite plate

2 无限板孔边裂纹解析权函数精度检验

为保证在任意载荷作用下K和COD的求解精度，必须对第1节得到的孔边裂纹权函数的精度作检验确认。文献中通常的检验方法是：用所求得的权函数计算在某些载荷情况下的K并与文献中的高精度解比较。尽管这种比较K的方法可以作为评价权函数的一种间接手段，但实际上存在着严重的弊端。因为仅对某些载荷情况的K进行比较，并不能真实和全面地反映权函数自身的精度。其主要原因是：① 由于在权函数的推导中对参考载荷情况使用了K自洽条件，故当新的载荷情况与参考载荷没有明显差别时，用权函数计算得到的K必然与参考解K的精度很接近(某种形式的“遗传性”)。但当新的载荷情况与参考载荷有明显差别时，用权函数计算得到的K就可能出现较大甚至非常大的误差；②K是由权函数m(α,γ)和裂纹面应力σ(ξ)的乘积沿整个裂纹长度α积分得到的，权函数的正/负误差可能会由于积分的平均效应相互抵消，从而降低了K的误差。所以用某些载荷情况下K的良好符合性来证明权函数本身的高精度，这种把多个因素交织在一起的做法，很可能造成假象并引起误导。

解决权函数精度评价问题的唯一可靠途径，是对与之相对应的格林函数进行比较[4,7-8,10]。格林函数表示在裂纹面受一对单位集中力(点载荷)P作用下的应力强度因子。利用格林函数评价权函数是对整个裂纹长度α范围(即0≤γ≤1.0)逐点进行比较，所以能排除权函数对参考载荷情况的偏向性和基于K的积分平均效应。这种基于格林函数的评价方法由于采用逐点检验的方式，因此能够准确反映权函数在裂纹面任意位置的精度。格林函数G(α,γ)与权函数m(α,γ)之间的关系非常简单[4]：

(9)

2.1 无限板孔边单裂纹的Shivakumar-Forman格林函数[12]

Shivakumar和Forman采用Muskhelishvili的复变函数理论[21]，得到了无限板孔边单裂纹(N=1)的格林函数值，并拟合给出了包含30个系数的二重多项式[12]。采用本文的变量定义，其拟合式为

(10)

式中：

多项式C(δ,γ)中的系数Cm,n如表4所示。

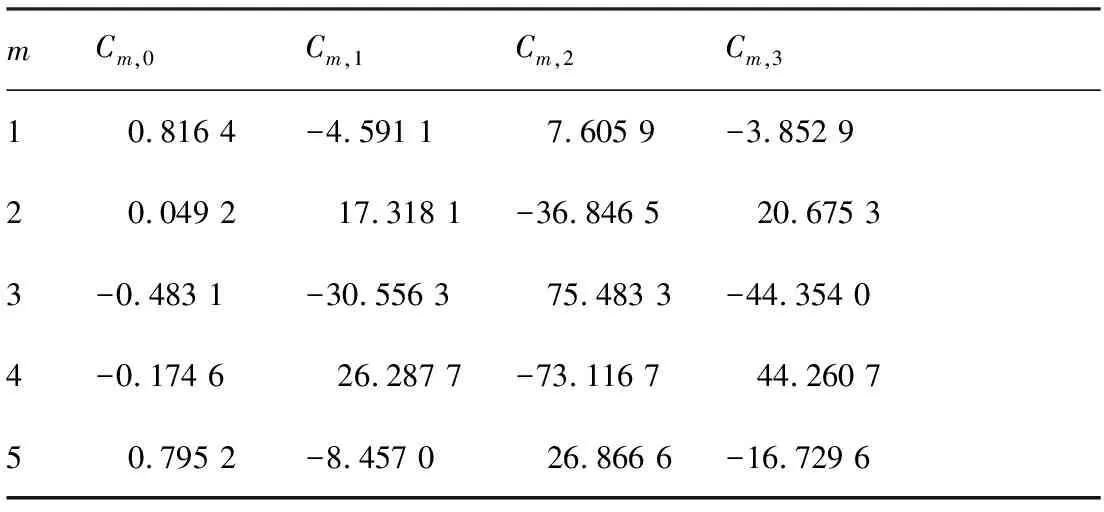
表4 式(10)中的系数Cm,nTable 4 Coefficients Cm,n in Eq. (10)

2.2 无限板孔边双裂纹的Newman格林函数[13]

Newman用边界配位法计算得到了无限板孔边双裂纹(N=2)封闭形式的格林函数拟合表达式[13]。采用本文的变量定义，其拟合式为

(11)

式中：

2.3 基于复变函数泰勒级数展开理论(WCTSE)的孔边裂纹权函数

Wagner和Millwater在2012年提出了一种基于泰勒级数展开理论和复变函数有限元分析的高精度数值权函数(WCTSE)法[9]。Jing和Wu对这种方法作了深入研究，进一步提高了其求解精度[10]。对共线中心裂纹和圆盘边缘裂纹等具有解析解的裂纹几何的验证表明，WCTSE法有很高的精度和鲁棒性[7-8, 10-11]。

WCTSE法给出的权函数是数值形式的，需要通过拟合才能得到封闭形式的权函数表达式。Jing和Wu[10]的研究表明，对边缘裂纹使用式(12)形式的拟合多项式能使权函数获得最佳精度：

M2(1-γ)2+…+Mn(1-γ)n]

(12)

本文利用WCTSE法，对孔边裂纹(N=1, 2)进行了复变有限元计算和权函数拟合。表5给出了按式(12)拟合的系数Mi。

2.4 无限板孔边裂纹Wu-Carlsson解析权函数的精度验证

将式(2)和式(12)分别代入式(9)可得到Wu-Carlsson解析权函数和WCTSE数值权函数的格林函数，并与Shivakumar-Forman(式(10))和Newman(式(11))的结果进行比较。

表5无限板孔边裂纹(N=1，2)WCTSE法权函数(式(12))的拟合系数Mi

Table5WCTSEcoefficientsMi(Eq.(12))ofradialcrack(s) (N=1,2)atcircularholeininfiniteplate

孔边单裂纹(N=1)Mii=1i=2i=3i=4α=0.1 0.417 4 0.198 8α=0.2 0.347 8-0.308 9 0.865 0-0.462 7α=0.5 0.048 2-0.093 0 0.442 6-0.247 5α=1.0-0.174 5 0.148 2-0.036 8α=1.5-0.199 0 0.019 4 0.012 4α=2.0-0.230 2-0.030 7 0.024 4孔边双裂纹(N=2)Mii=1i=2i=3α=0.10.331 90.394 6-0.117 9α=0.20.292 20.197 5α=0.50.167 40.149 5α=1.00.138 20.117 3α=1.50.144 30.109 3α=2.00.157 20.105 9

2.4.1 孔边单裂纹

对于孔边单裂纹(N=1)，本文得到的Wu-Carlsson解析权函数与Shivakumar-Forman[12](式(10))和WCTSE法的结果均符合良好(见图2(a))。所对应的格林函数与式(10)的差别基本在±2.0%以内(见图2(b))；与WCTSE法最大差别约为2.0%(见图2(c))。

这里需要指出，本文的解析权函数(N=1)和WCTSE法在γ=0时的格林函数符合很好(见图2(c))，而Shivakumar-Forman公式[12]结果比其他2种方法偏高约3%，见表6。由此可以推断，图2(b)中在γ=0附近稍大的差别很可能是文献[12]的精度偏低造成的。

αWu-CarlssonWCTSEDifference/%Shivakumar-Forman[12]Difference/%0.51.629 51.626 8-0.171.676 12.91.01.325 11.325 0-0.011.367 03.21.51.174 91.177 8 0.241.207 32.8

2.4.2 孔边双裂纹

对于孔边双裂纹(N=2)，本文得到的Wu-Carlsson解析权函数与Newman[13]和WCTSE法的结果均符合良好(见图3(a))，所对应的格林函数与Newman的式(11)以及WCTSE格林函数的差别都不超过2%(见图3(b)和图3(c))。

以上比较表明，本文求得的孔边单/双裂纹Wu-Carlsson解析权函数不但具有很高的精度，而且是以无量纲裂纹长度α为变量的封闭解，能够方便确定任意裂纹长度(0≤α≤2.0)的权函数解，这对疲劳裂纹扩展和寿命预测计算是十分有利的。采用这种统一的权函数解法，仅需变换K和CMOD参考解的多项式拟合系数即可分别求解孔边单/双裂纹问题。

最近Jin等[14-15]采用Glinka-Shen的基于2种参考载荷应力强度因子解的方法[6]得到了孔边裂纹(N=1, 2)数值形式的权函数，进而通过拟合给出了封闭形式的孔边裂纹权函数表达式。Jin等利用这些权函数计算的几种其他载荷情况的K与文献中的解符合良好，进而据此认为其权函数的精度得到了验证。如前所述，实际上这种基于K的“验证”很容易误导。本文作者通过对权函数所对应的格林函数比较，对文献[14-15]给出的权函数(表格数值和拟合公式)逐点进行了精度检验，发现其孔边单/双裂纹的权函数均存在显著误差：孔边单裂纹结果与Shivakumar-Forman[12]及本文的解析权函数最大差别达±200%，如图4所示；孔边双裂纹与Newman解[13]的差别虽然明显小于单裂纹情况，但也达-8%～14%，如图5所示。图6则进一步给出了孔壁楔形加载时的应力强度因子差别，可见文献[15]的孔边单裂纹结果与其他3种权函数的结果差别极大。本文作者已对Jin等孔边裂纹权函数[14-15]的精度问题提出质疑[22]。在此提请读者注意。

3 应用高精度解析权函数求解孔边裂纹问题

利用本文得到的高精度解析权函数可以高效求解各种复杂载荷情况下的孔边裂纹问题，下文给出代表性的3种载荷情况的K计算结果。

3.1 裂纹嘴楔形载荷

考虑孔边裂纹承受楔形载荷(即作用在裂纹嘴处的一对集中力P)，如图6所示。该集中力可以表示为σ(ξ)/σ0=Pδ(0)，δ(0)是Dirac函数。此时的应力强度因子实际上就是孔边裂纹在γ=0点的格林函数。用式(2)和式(3)确定的解析权函数的计算结果如图6所示。Wu-Carlsson权函数结果与Shivakumar-Forman[12](N=1)和Newman[13](N=2)的解，以及与WCTSE结果之间的差别均不超过2%。而Jin权函数结果则明显偏离，其单裂纹的K在α=0～0.16范围甚至为负值(见图6(a))，这显然有悖于物理规律。

3.2 裂纹面多项式分布载荷

考虑裂纹面承受如图7所示的幂函数分布应力。该载荷形式可以表示为

σ(ξ)/σ0=ξn

(13)

将式(13)和式(2)分别代入式(1)即可得到孔边裂纹无量纲应力强度因子的Wu-Carlsson解析权函数解fn。经适当化简，fn可以写成包含系数βi(α)的解析表达式[4, 7-8]为

(14)

将式(3)的βi(α)代入式(14)得到孔边裂纹在幂函数分布应力作用下的应力强度因子fn。为方便使用，表7列出了部分结果。

在很多情况下，连续分布的裂纹面应力可用无量纲坐标ξ的多项式表示。根据叠加原理，若孔边裂纹裂纹面承受多项式分布载荷为

σ(ξ)/σ0=∑Cnξn

(15)

则对应的应力强度因子可由幂函数应力引起的无量纲应力强度因子fn计算得到：

f=∑Cnfn

(16)

需要注意的是，式(14)中的积分上下限分别为0和α，因此表7中给出的fn仅适用于应力分布在整个裂纹面上的情况(0≤ξ≤α)。

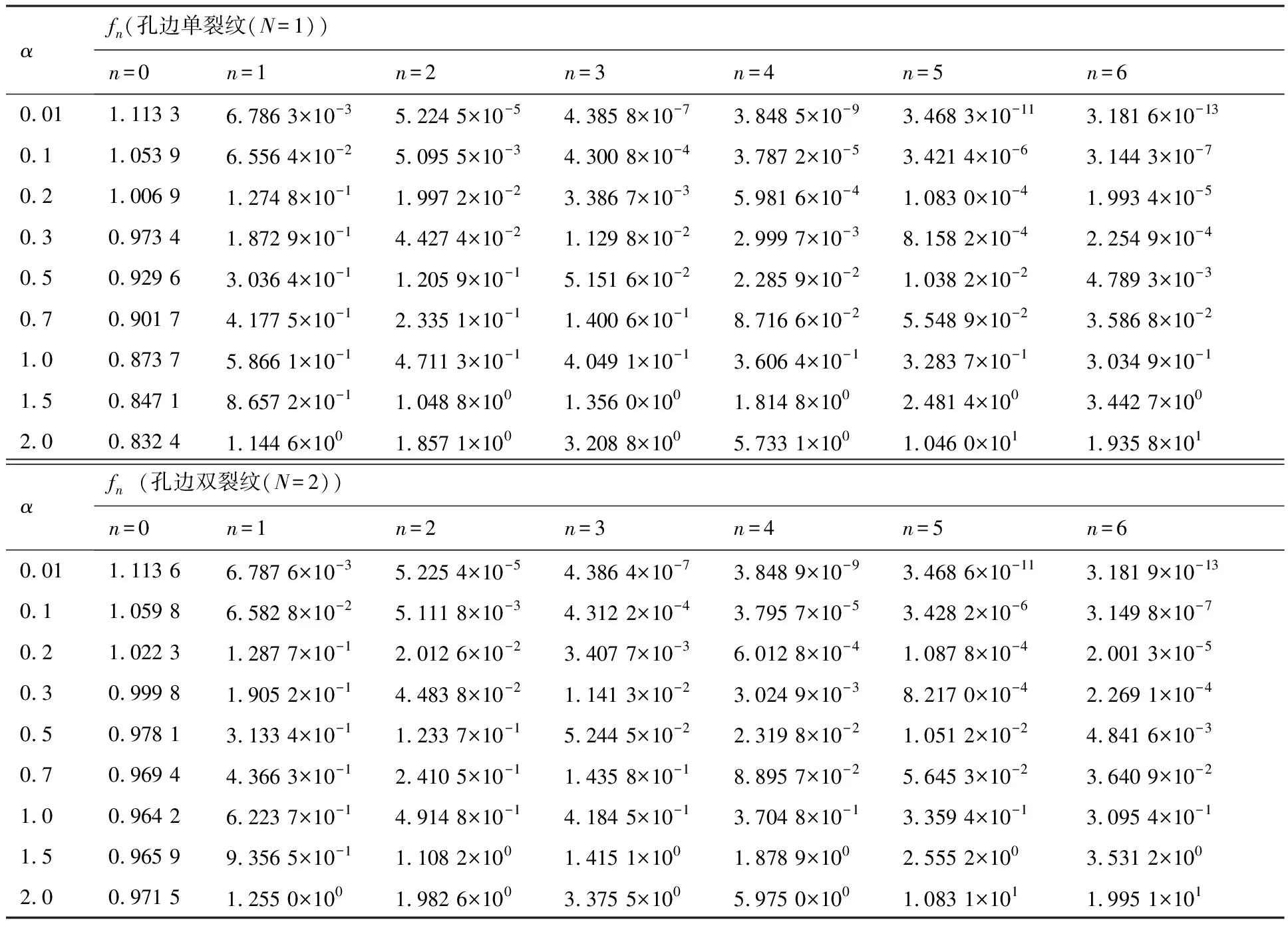
表7 孔边裂纹在裂纹面幂函数分布载荷(σ(ξ)/σ0=ξn)下的无量纲应力强度因子fnTable 7 Dimensionless SIFs fn of radial crack(s) at circular hole under power stress (σ(ξ)/σ0=ξn) on crack surfaces