柔性电子薄膜热弹耦合振动分析
2022-09-26武吉梅邵明月
冯 谣, 武吉梅, 邵明月
(1.西安理工大学 机械与精密仪器工程学院, 陕西 西安 710048;2.西安理工大学 印刷包装与数字媒体学院, 陕西 西安 710048;3.浙江交通职业技术学院 汽车学院, 浙江 杭州 311112)
柔性电子薄膜因其“薄”、“柔”的优良特性而被广泛应用于各类电子产品中,伴随着中国经济的发展,柔性电子薄膜的需求量逐年加大。在柔性电子薄膜的印刷过程中,烘干机会对其进行加热烘干,而温度变化会影响柔性电子薄膜的振动特性,造成高速运动的柔性电子薄膜剧烈抖动,影响柔性电子薄膜的套印质量。因此,研究热弹耦合作用下运动柔性电子薄膜的振动特性,得到不同参数下受温度影响的柔性电子薄膜的振动规律,对柔性电子薄膜印刷机的设计、制造以及稳定性分析具有重要意义。
目前,很多学者研究了热弹耦合作用下运动梁、板、扇形板的振动特性,但对热弹耦合作用下运动薄膜的振动稳定性研究较少。Lin等[1]采用非线性板方程,描述了横向荷载作用下具有小弯曲刚度的宽幅轴向移动腹板的运动,该模型可以模拟纸或塑料板。Jiang等[2]使用解析解方法,研究了轴向热应力作用下非局部Euler梁的自由振动。Saksa等[3]采用线性Kirchhoff板理论,用复变函数法分析了正交各向异性薄板的轴向运动。Saini等[4]在经典Kirchhoff板理论基础上,利用Hamilton原理得到了热弹性平衡和振动控制方程以及前三阶模态的热位移和频率。Xin等[5]建立了一个考虑两种典型梯度热环境的简支板,采用模态分解法求解热声响应控制方程。Yang等[6]利用Hamilton原理建立了随从力作用下扇形板热弹耦合微分方程,使用微分求积法得到了扇形板前三阶的无量纲复频率。Wu和 Shao等[7-8]基于Von Karman大挠度理论建立了运动薄膜非线性强迫振动方程组,研究了薄膜无耦合工况的振动。Dan等[9]开发了MATLAB非线性有限元程序,用于预测柔性电子薄膜运行过程中的温度场和应力场。Lee等[10]通过考虑辊对辊系统干燥过程中温度波动引起的热应变,扩展了Shin提出的运动板张力数学模型,提出了一种新的基于扩展模型的控制方案,以消除干燥过程中由于热应变引起的张力扰动。Li等[11]研究了功能梯度夹层板在热载荷作用下的弯曲响应,得到了体积分数、几何参数和热载荷对功能梯度夹层板的挠度的影响。文献[12]利用微分求积法研究了梯度多孔圆板的热振动特性,得到了空隙分布模式、空隙率系数、温升等因素对固有频率的影响。Mirtalaie[13]使用微分求积法研究了功能梯度扇形薄板在热环境中的自由振动特性,得到了温度场、体积分数、半径比和扇形角对功能梯度扇形薄板自由振动的影响。Zhao等[14]研究了轴向运动微纳梁的热弹耦合强迫振动,发现轴向运动微纳梁的固有频率随轴向速度、小尺度参数和高长比的增大而减小。
综上,上述文献鲜见对热载荷作用下运动矩形薄膜横向振动特性的研究。因此,本文将建立考虑温度作用的运动薄膜横向振动的动力学方程,使用微分求积法对该动力学方程进行离散化处理,并分析热弹耦合作用下运动薄膜的振动特性。
1 振动模型的建立
图1为对边张力作用下热弹耦合振动柔性电子薄膜的动力学模型。图中v为纵向移动速度,a、b为印刷机构导向辊之间柔性电子薄膜的长度和宽度,柔性电子薄膜高为h,密度为ρ,弹性模量为Ε,泊松比为μ,柔性电子薄膜线膨胀系数为αT,设横向振动位移为w(x,y,t),Tx与Ty为单位长度张力,T0为柔性电子薄膜的初始温度,假设柔性电子薄膜温度变化为T=T(x,y,z,t)。
根据Hamilton原理,热弹耦合薄板的振动方程为:
(1)
如图2所示,取柔性电子薄膜的一个微元体dxdy进行分析,柔性电子薄膜变形后的等效合力为:
(2)
(3)
根据D’Alembert原理,含有对边张力作用的柔性电子薄膜的热弹耦合振动方程为:
(4)
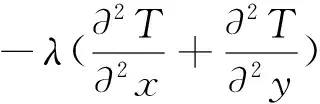
(5)
式(4)中变量MT含有温度T,式(5)中含有挠度w,得到方程组:
(6)
(7)
将下列量无量纲化:
并代入式(6)、(7)得到其无量纲化的形式:
(8)
(9)
其中,
设式(8)、(9)的解为:
(10)
将式(10)代入式(8)、(9),得到无量纲化的运动柔性电子薄膜的振动微分方程:
(11)
(12)
对式(12)进行求解,得:
(13)
其中,c1,c2为待定系数。将式(13)代入式(11),化简得:
(14)
柔性电子薄膜在运动的过程中,四周有滚轴和毛刷的支撑,因此其边界条件可简化为四边简支:
(15)
2 方程求解
使用微分求积法对式(14)进行离散,得到复特征值方程:
(16)
运动薄膜的边界条件为:
(17)
将式(16)、(17)合并成矩阵形式,得到运动柔性薄膜热弹耦合振动的特征方程:
|ω2R+ωG+K|=0
(18)
式中:R为单位矩阵;G、K为包含长宽比的热弹耦合系数的矩阵。
3 数值分析
以陕西北人FR400ELS精密涂布机为例,分析不同热弹耦合系数ϑ、张力比k对运动薄膜振动特性的影响。凹版印刷机的基本参数如表1所示。
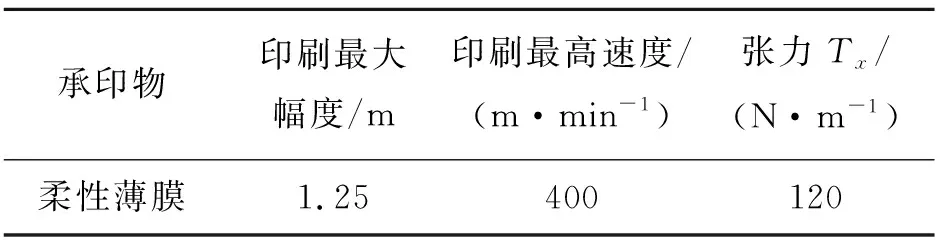
表1 陕西北人FR400ELS凹版印刷机的基本参数
为验证微分求积法应用于本例的有效性,令ϑ=0,此时式(14)退化为无热风作用的薄膜横向振动方程,设节点数N=11,分别求出长宽比r0=1.0、r0=2.0时的运动薄膜的复模态,并将此复模态与文献[15]进行对比,结果如表2所示。

表2 本文解与文献[15]解析解的对比(ϑ=0,k=0.2,c=0.164)
由表2可知,微分求积法得到的结果与文献[15]解析解得到的结果有很好的一致性,说明可以使用此方法研究运动薄膜的热弹耦合振动特性。
3.1 热弹耦合系数对柔性电子薄膜振动的影响
图3给出了r0=1.0,k=1.0,ϑ=0.1时,柔性电子薄膜运动的复模态随无量纲速度c的关系曲线。当c<2.505时,前三阶复模态的实部为实数,虚部为0;当2.505≤c≤2.705时,第一阶模态的实部为0,虚部向两边发散,说明运动柔性电子薄膜此时发散失稳,这时系统是不稳定的;当c=2.904时,第一阶模态与第二阶模态发生耦合,此时柔性电子薄膜运动系统发生耦合颤振。
图4给出了r0=1.0,k=1.0,ϑ=0.3时,柔性电子薄膜运动的复模态随无量纲速度c的关系曲线。与图3相比,当c<3.802时,运动薄膜前三阶复模态的实部增大,说明随着热弹耦合系数的增加,运动薄膜处于稳定工作状态的区间增大;当3.802≤c≤4.401时,运动薄膜处于发散失稳状态;当4.401≤c时,系统重新恢复稳定;当c=4.706时,前两阶模态发生耦合,此时运动柔性电子薄膜发生耦合颤振。比较图3、图4可以发现,随着热弹耦合系数的增加,运动薄膜的前三阶复频率增大,且第一阶复频率的临界速度同时增加。
3.2 张力比对柔性电子薄膜振动的影响
图5和图6给出了r0=1.0,ϑ=0.3,k分别取0.5和1.0时,运动薄膜前三阶复模态与无量纲速度c之间的关系曲线。由图5可以看出,当c<3.702时,第一阶模态的实部为实数,运动薄膜处于稳定的工作状态;当3.702≤c≤4.401时,第一阶模态的实部为0,虚部向两边发散;当c=4.700时,第一阶模态与第二阶模态耦合。
图6给出了张力比k增加到1.0时,运动薄膜前三阶复模态与无量纲速度c之间的关系曲线。当张力比k增加时,第一阶模态的实部处于稳定工作状态的区间增大。当3.802≤c≤4.401时,运动薄膜处于不稳定状态;当c=4.700时,第一阶模态与第二阶模态耦合。可见,张力比的增加会使薄膜稳定工作的区间增加。
4 结 论
本文研究了运动柔性电子薄膜热弹耦合振动下的振动特性。基于D’Alembert原理构造了热风作用下的运动薄膜振动方程,使用微分求积法进行求解,并分析了运动薄膜前三阶复模态与各参数之间的关系曲线。
1) 当热弹耦合系数ϑ=0时,动力学模型退化为不含热风作用的振动方程,将本文解的前三阶复频率与文献解析解的前三阶复频率进行对比,验证了微分求积法的有效性。
2) 运动薄膜在烘干机的热风作用下会产生耦合振动,当其他参数不变时,增大热弹耦合系数,运动薄膜的前三阶复频率会增大,同时,第一阶模态与第二阶模态将产生耦合共振,此时运动薄膜会发生褶皱、裂纹甚至断裂,因此,需要控制精密涂布机的烘箱温度,以避免耦合颤振的发生。
3) 当其他参数不变,张力比k由0.5增大到1.0时,运动薄膜第一阶模态发散失稳时的临界速度增大,表明适当增加运动薄膜的张力比,能使运动薄膜稳定工作的区间增大。
