单螺杆压缩机啮合副油膜流场数学模型研究

2022-09-26陈国庆孙帅辉

西安理工大学学报 2022年2期

黄锐，夏天，陈国庆，孙帅辉

(西安理工大学西北旱区生态水利国家重点实验室，陕西西安 710048)

单螺杆压缩机属于容积式压缩机的一种，已被广泛应用于空气压缩、制冷剂压缩以及化工气体压缩等领域。单螺杆压缩机结构如图1所示，其主要零件包括星轮、螺杆以及包围螺杆和星轮的机壳。在工作过程中，螺杆由电机拖动旋转，星轮齿面、机壳内壁和螺杆螺槽形成不断缩小的密闭腔，当密闭腔内气体达到设计压力时，密闭腔与机壳上的排气通道联通，压缩气体排出。通常将一个螺杆和一个星轮称为一对啮合副。

单螺杆压缩机的星轮齿面(即啮合区域)容易磨损，如图 2所示。吴伟烽、李挺[1,2]等提出，星轮齿磨损的原因主要是星轮齿受到了不平衡的周向油膜力矩。当润滑油流经啮合副间隙时，间隙内产生油膜压力场，该压力场推动星轮齿面背离螺槽表面，使星轮齿发生偏转。由于星轮齿两侧均有润滑油流过，两侧均受到油膜力作用，当油膜力一侧过大，另一侧过小时，可使星轮齿转向受力较小的一侧，使得受力较小侧的星轮齿面与螺槽表面发生金属接触，最终发生磨损。因此，准确地计算油膜压力场是解决星轮齿磨损问题的关键。

目前，对啮合副间隙内油膜压力场的计算主要有两种模型。一种是Post等[3,4]提出的(本文称其为Post模型)。Post和Zwaans最早对啮合副油膜作用力进行了研究，他们假设润滑油沿星轮齿长方向无流动，将B.E Launder轴承润滑模型[5]引入啮合副油膜压力场的计算中，对单直线型面和单圆柱型面啮合副间隙内的油膜压力分布进行了计算。Sun等[6]在Post模型基础上，对单直线包络型面啮合副间隙内，油膜压力随间隙宽度的变化规律进行了分析。然而，在啮合副啮合过程中，星轮齿不同齿长处的相对速度与螺槽的相对速度不等，在Post和Sun的研究中，并未涉及不同相对速度的处理方式。

为了进一步考虑星轮齿不同齿长处相对速度的不同对油膜压力场的影响，Huang等[7-9]提出了另一种模型，即油膜压力分段计算模型(本文称为模型1，下同)。该模型将星轮齿面沿齿长方向分成众多微元段，假设星轮齿与螺槽的相对速度在每一个微元段内保持不变，采用B.E Launder轴承润滑模型对每一个微元段内的油膜压力分布进行求解，进而得出整个齿面上的压力分布。Huang等还在该模型基础上，提出了一种基于平衡星轮周向力矩的圆柱类包络型面的优化方法。Li等[10]在Huang的基础上，对采用单直线型面、单圆柱型面和多圆柱型面的啮合副间隙内的水膜压力进行了比较。Li等[11]还对单直线型面、单圆柱型面和多圆柱型面啮合副的油膜力特性开展了实验研究，通过测量自平衡实验和加载实验中的星轮齿偏角，间接证明了油膜压力分段计算模型的计算结果与实验结果基本一致。Liu等[12]认为，可通过油膜压力分段计算模型，计算多圆柱包络型面的星轮齿两侧的油膜压力场，进而得到星轮齿周向力矩，并通过调整圆柱位置来平衡周向力矩。油膜压力分段计算模型也是基于润滑油在星轮齿长方向无流动(即微元段与微元段之间无流动)这一假设发展起来的。然而，由于星轮齿上表面为压缩腔的高压区，而星轮齿根处于星轮腔中，星轮腔的压力是常压，在压差的作用下，必将有润滑油沿星轮齿长方向的流动，以及润滑油向齿根处的泄漏(端泄)。那么，忽略润滑油在齿长方向的流动，对油膜流场的影响有多大，目前还未见文献报道。另外，以上两种模型均未考虑润滑油在啮合副间隙发散段的空穴现象，而空穴现象也会对油膜流场产生影响[13，14]。

基于以上分析，本文采用SolidWorks软件，构建了实验台啮合副三维间隙几何模型，采用ANSYS ICEM软件对计算域进行提取和结构网格划分，基于质量守恒方程、动量守恒方程、RNGk-ε湍流模型、Mixture 混合模型以及Sing Hal-Et-Al空穴模型，考虑了沿星轮齿长方向上的润滑油流动和几何扩散区域的空穴现象，提出了油膜流场数值模拟计算模型(称为本文模型或模型2，下同)，搭建了啮合副油膜流场压力测试实验台，并基于ANSYS FLUENT对实验台啮合副间隙内的油膜压力场进行模拟，将实验结果与本文模型和模型1进行对比分析，考察了两种数学模型的精确度和适用性。结果表明，本文模型准确度更高，适用范围更广。

1 数学模型

1.1 油膜压力分段计算模型(模型1)[7-9]

油膜压力分段计算模型中，将星轮齿面划分为若干个微元段dl，如图 3(a)所示。微元段内的间隙几何模型如图 3(b)，在每一个微元段内，其间隙形态沿啮合副相对运动速度U的方向呈现先收敛后扩张的特点。

B.E Launder轴承润滑模型的表达式为：

(1)

式中：P为间隙内的油膜压力，Pa；μ为润滑油的动力粘度，Pa·s-1；h为间隙宽度，mm；U为星轮齿面与螺槽表面在微元段上的相对运动速度，m·s-1；ρ为润滑油密度，m3/kg；α=1.2；β= 0.133；um为流体在窄缝内的平均质量流速：

式中：u为润滑油在y方向上的速度分布。

连续性方程和Gumbel压力边界条件为：

(2)

(3)

式中：Pin为密封腔压力，Pa；Pout为低压腔压力，Pa。

对式(1)进行积分，将式(2)和式(3)代入积分后的式(1)，并进行整理化简，具体推导过程可参考文献[7]～[10]，最终得出微元段间隙内的油膜压力分布计算模型：

(4)

ρβU2[lnh(x)-lnh(x0)]

其中：

计算油膜压力分布时，需根据设计参数得出不同星轮齿长处啮合副的相对速度U，将其代入式(4)，即可求得啮合副间隙内收敛段的油膜压力分布。当润滑油流经发散段时，根据Gumbel压力边界条件的假设，润滑油压力与收敛段出口边界条件的压力值相同。

从图3和式(1) ～ (4)可看出，各微元段间隙内的油膜流场压力分布为x的函数，油膜流场压力梯度在微元段内沿l方向保持不变。微元段内的油膜流场与相邻微元段无关，润滑油在星轮齿长方向上无流动。然而，在啮合副实际啮合过程中，润滑油存在朝星轮齿根处的泄漏(端泄)，因此忽略润滑油沿l方向上的流动不符合实际情况。另外，在啮合副间隙扩散段，由于几何空间突然扩大，润滑油在扩散段必然产生负压区和空穴现象，而模型1并未考虑负压区的存在，亦与实际情况不符。最后，模型1未见有直接实验验证。

1.2 数值模拟计算模型(模型2)

1.2.1流体域提取及网格划分

单螺杆压缩机最常见的三种型面为单直线型面、单圆柱型面和两圆柱型面。采用SolidWorks和ANSYS ICEM软件对实验台三种型面的啮合副间隙进行建模和计算域提取(见图 4)，并进行结构网格划分。以单直线型面为例，分别在网格数量为184万、343万、679万时，对截面1(距离星轮齿面0点位置14 mm)和截面2(距离星轮齿面0点位置40 mm)处的油膜压力曲线进行比对，如图5所示。无关性验证中，假设油膜入口压力为4.05×105Pa，螺杆转子转速为1 200 r/min。从图5可看出，343万网格和679万网格得出的计算结果非常接近，因此，最终选取的网格数量为343万，网格细节如图 6所示。单圆柱型面和两圆柱型面的网格节点设置与单直线型面相同。

实验台啮合副(三种型面)间隙的计算域尺寸如图7所示。

1.2.2控制方程

润滑油在间隙收敛段为纯液状态，但在间隙扩张段，几何空间突然变大，润滑油压力急剧下降，润滑油内溶解的气体析出。此时，润滑油成为两相流，需引入两相流模型。本文采用两相混合模型(Mixture model)，Mixture model在滑动轴承油膜压力场计算中常被采用，其计算精度和稳定性已经得到了广泛认可[13]。两相混合模型下的连续性方程、动量方程和能量方程为：

∇·(ρmvm)=0

(5)

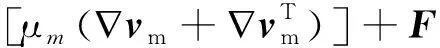
(6)

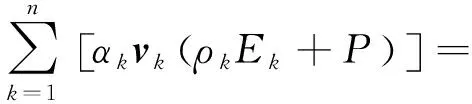
(7)

式中：ρm为混合相平均密度，kg·m-3；νm为混合相平均速度，m·s-1；μm为混合相粘度，m2·s-1；F为混合相惯性力，N；αk为第k相的体积分数；ρk为第k相的密度，kg·m-3；νk为第k相的速度，m·s-1；Ek为第k相的内能与动能之和，J·kg-1；keff为混合相的有效热传导率。

针对润滑油的空穴现象，需考虑空穴模型，Sing Hal-Et-Al模型是滑动轴承计算领域中常采用的空穴模型[13]。该模型考虑了相变、气泡运动、湍流压力波动和不可凝气体对气相生成率和凝结率的影响[15]，考虑因素较为全面，也被称为全空穴模型。空穴模型液相、气相、混合相的两相流连续性方程描述如下：

(8)

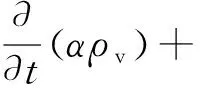
(9)

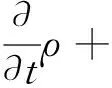
(10)

式中：α为气相体积分数；ρl为液相密度，kg·m-3；ρv为气相密度，kg·m-3；Vv为混合相速度，m·s-1；Re为气相生成率；Rc为气相凝结率；Re-Rc为气液两相间的质量输运。

本文中，螺杆转子转速较高，且啮合副间隙宽度较小，壁面曲率较大，对流场影响很大，除了两相混合模型和空穴模型外，考虑到空穴区域可能会引起漩涡，还需要考虑湍流模型，而RNGk-ε湍流模型适用于计算流场紧贴弯曲壁面的流体，故被本文采用。

1.2.3软件设置

转子转速分别设为800 r/min和1 200 r/min，润滑油入口压力为4.05×105Pa，出口压力设为常压。润滑油动力粘度根据ASTM推荐的双对数形式的Walther方程，由2.1节实验方案中实验段入口处测得的润滑油温度来确定。

(11)

式中：T为开尔文温度；α为经验系数，本式中α= 0.77cSt；A和B是待定常数，根据46号润滑油在40 ℃和100 ℃下的动力粘度来确定。

1.3 两种模型的计算结果对比

对两种数学模型的计算结果进行对比。鉴于啮合副间隙内重点关注的是油膜压力，因此，主要对压力场进行对比分析。

1.3.1压力场对比

两种模型得出的星轮齿侧油膜压力场如图 8所示。由图可看出，在两种转速下，模型1和模型2计算得出的实验星轮齿啮合线前侧均出现了高于压缩腔压力的压力区。由于齿面与螺槽面间隙具有先收敛，后扩张的特点(见图7)，当润滑油流入收敛区域时，由于速度流动引起的单位长度上的流量从入口处到最小间隙处逐渐减小，为了保证各断面处的流量相等，啮合线前端必然产生高压区，该高压区域也称为油膜的承压区或正压区。在发散段，由于模型1采用了Gumbel压力边界条件，因此模型1的计算结果为常压；模型2中考虑了发散段几何特征对油膜压力场的影响，因此模型2的云图中出现了负压区。

星轮齿面越靠近螺杆外侧(即星轮齿根处)，星轮齿面与螺槽的相对速度越大，油膜动压效应越明显，则该位置的油膜压力峰值相对于其它位置越高。在模型1中，由于未考虑端泄，其油膜压力峰值最高点出现在l= 0 mm的截面上；而在模型2中，考虑了润滑油在齿根处的泄漏，其油膜压力峰值最高点并未出现在星轮齿根位置，而出现在l=7 mm左右的截面上。从图 8中还可看出，在间隙收敛段，模型1得出的油膜正压区面积较大，正压值较高，说明在不考虑端泄的情况下，间隙收敛区的油膜承载力大于考虑端泄时的油膜承载力。

在间隙发散段，润滑油流过最小间隙(啮合线处)后，啮合副间隙的几何空间突然增大，油膜压力急剧降低，油膜压力减小导致油膜切向压力分量减小，没有足够的润滑剂填充继续增大的间隙空间，润滑油中溶解的空气析出，油膜发生破裂。模型2考虑了润滑油流经间隙发散段时产生的空穴现象以及空穴现象发生时星轮齿面所受的压力。发散段的星轮齿面受到的最小压力为气体从润滑油中溢出时的空气分离压(约为7 550 Pa)，远小于Gumbel压力边界条件假设的常压。因此在发散段，模型1得出的油膜压力亦大于模型2得出的油膜压力。综上所述，在采用模型1计算星轮齿全齿面受到的油膜压力时，得出的油膜承载力大于模型2的油膜承载力。

1.3.2气相分布

模型2加入了空穴模型，得到了空穴现象发生时星轮齿面上的气相体积分布，如图9所示。由图可看出，星轮齿面的扩散区均有气相产生，且气相分布面积和体积分数值与转子转速和星轮齿型面结构相关。在相同型面结构下，随着转子转速的增加，齿面扩散段负压区面积增加，且负压区的压力值更低(参照图 8)，润滑油中溶解空气的析出区域扩大，因此，气相体积分数及气相分布面积亦随之增加。对比图9中(a)和(c)、(b)和(d)可发现，单圆柱型面比单直线型面更易发生空穴现象。对于两圆柱型面，其扩散段长度较短，当润滑油流入扩散段时，受到出口处常压的影响，油膜压力可迅速恢复到常压。空穴现象的产生有利于提高星轮齿侧油膜负压区的最小压力，可在一定程度上增大星轮齿面周向受力。但空穴现象发生时，润滑油内气泡的析出和溃灭可能会导致星轮齿表面发生汽蚀破坏，从而增加星轮齿磨损的可能性。

2 实验验证与结果讨论

为了对模型1和模型2计算结果的准确性和适用性进行考察，本文搭建实验台，对模型1和模型2进行实验验证。

2.1 实验方案

实验系统如图10所示。实验段入口、出口管道及实验段高压腔内的油压采用青岛华青压力表测量。实验段入口高压油温采用XMT-SF405S温度传感器(精度1.0%)测量。啮合副间隙内的动态油压采用HM91-H3压力传感器(量程-0.1～1.0 MPa，精度±0.25%，最大频响200 kHz)测量。数采卡型号为HL300。

实验段原理如图11所示，实验星轮齿上表面、转子侧壁、密封壳和密封板组成高压腔。实验过程中，通过持续地向高压腔内注入高压油，使高压腔内维持一定的压力。转子由电机带动旋转。压力传感器探头安装在转子侧壁，随转子同步旋转。当探头扫过实验齿面时，可测得啮合副间隙内的动态压力。压力传感器信号线通过集流环与数采卡相连，压力信号通过数采系统实时保存。

本文以常见的单直线型面、单圆柱型面、两圆柱型面的星轮齿为测试对象，如图12所示。

实验段中，转子外径160 mm，转子槽底半径95 mm，槽深65 mm，星轮齿啮入长度为65 mm，压力传感器探头安装在半径为146 mm的转子壁面处。三种实验齿的型面几何尺寸与图7保持一致。

实验台转子转速与数学模型保持一致，分别调整在800 r/min和1 200 r/min。高压腔压力控制在4.05×105Pa，低压腔压力为常压。实验台选用的润滑油为46号润滑油。

2.2 实验结果与讨论

本文根据传感器安装位置，对图8中l= 14 mm的星轮齿截面处的压力值进行提取，并与实验结果进行对比，如图13所示。

单直线型面下，当螺杆转子转速为800 r·min-1时，模型1的油膜压力峰值为5.06×105Pa，模型2的油膜压力峰值为4.84×105Pa，仅相差4.5%；当转速为1 200 r·min-1时，模型1的油膜压力峰值为5.97×105Pa，模型2的油膜压力峰值为5.40×105Pa，相差10.6%。当星轮齿采用单圆柱型面，转速分别为800 r·min-1和1 200 r·min-1时，模型1与模型2中的压力峰值分别相差21.9%和29.8%。当星轮齿采用两圆柱型面，转速分别为800 r·min-1和1 200 r·min-1时，模型1与模型2中的压力峰值分别相差28.8%和39.6%。这说明模型1和模型2的计算结果与型面和转速有关。仅考虑收敛区域时，单直线型面下两者的计算结果最为接近，两圆柱型面的计算结果差别最大。在低转速区域，两种模型计算结果的接近程度均大于高转速区域。

比较实验结果可知，模型2的计算结果更为精确，与实验结果契合度更高。当型面为两圆柱型面，且螺杆转速为1 200 r·min-1时，模型1与模型2的压力峰值相差最大，为39.6%。而模型1偏离实验结果较远，其偏离程度在单直线型面、小转速状态下最小，在两圆柱型面、高转速状态下最大。