维数分裂无单元Galerkin方法中权函数的研究
2022-06-09刘卫桃孟智娟李兴国任红萍
刘卫桃,孟智娟,李兴国,任红萍
(太原科技大学 应用科学学院,太原 030024)
无网格方法是一种只需要节点信息,不需要划分网格的方法。在处理不连续、大变形等数值问题时很有优势,因此在计算科学中的研究已很热门[1-3]。1992年,Nayroles等将Galerkin方法与移动最小二乘法(MLS)结合,提出了扩散单元法(DEM)[4].但DEM方法边界条件不易引入,对此Belystschko等人将DEM法进行了改进,提出了无单元Galerkin方法(EFG)[5],是无网格方法中最具有发展前景的方法之一,并且利用该方法处理了动态裂纹扩展和大变形等复杂的三维问题。Zhang等人提出了改进的无单元Galerkin方法(IEFG),并求解了热传导等问题[6]。
为提高无网格方法的计算速度,Ren等人提出了插值型EFG方法,且应用于求解弹性力学问题、三维弹塑性等问题[7-8]。张国达等人[9]研究了瞬态热传导问题的插值型EFG方法及误差。针对求解三维问题时计算量大、计算效率低的问题,孟智娟提出的维数分裂无单元Galerkin方法(DSEFG)[10]解决了这一问题,并将其应用于求解三维势问题等。
由于DSEFG方法中构造形函数[11]时权函数[12]的选择会直接影响计算的精度和效率,因此研究权函数的选取具有关键意义。
1 三维势问题的分维处理
三维势问题的控制方程为:
(1)
本质边界条件为:
(2)
自然边界条件为:
(3)
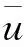
取x3为分裂方向,将问题域Ω在x3方向上分裂为L层。便得到L+1个二维子域Ω(k),(k=0,
1,…,L),则有:
(4)

(5)
相应的边界条件为:
(6)
(7)
对于求解问题(1)-(3)的数值解,选用的DSEFG方法是用IEFG方法求解二维边值问题,在分裂方向x3上采用有限差分法。
采用罚函数法施加于Γu,则有:
(8)
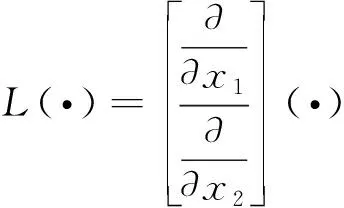
(9)
2 三维势问题的维数分裂无单元Galerkin方法(DSEFG)
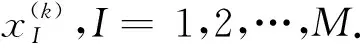
(10)
2.1 权函数类型
(1)三次样条函数
(11)
(2)四次样条函数
(12)
(3)正定紧支径向基函数(CSBRF2)
(13)
(4)指数型函数
(14)
2.2 三维势问题的维数分裂无单元Galerkin方法
由方程(10),可得:
Φ*(x(k))u″
(15)
(16)
这里
(17)
B(x(k))=
(B1(x(k)),B2(x(k)),…,Bn(x(k)))
(18)
(19)
将式(10)、式(15)-式(16)代入式(8)可得:
(20)
方程(20)的各项积分可讨论为:
δuT·C·u″
(21)
δuT·K·u
(22)
(23)
(24)
δuT·Kα·u
(25)
(26)
其中:
(27)
(28)
(29)
(30)
(31)
(32)
将式(21)-式(26)代入方程式(20)得:
δuT·(Cu″-Ku+Kαu-F1-F2-Fα)=0
(33)
由δuT的任意性,可得:

(34)
其中
(35)
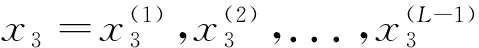
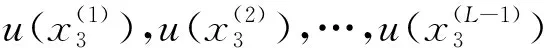
(36)
⋮
(37)
在x3上采用有限差分法,得:
(k=1,2,…,L-1)
(38)
从而,方程组(34)表示为:
(39)
⋮
(40)
其矩阵形式为:
(41)
这里
(42)
令
(43)
(44)
(45)
这样,方程(41)简化为:
EU=R
(46)
(47)
3 数值算例
在算例中,通过对三维势问题计算结果收敛性的研究,说明了权函数在维数分裂无单元Galerkin方法中的重要性。算例中的每个积分单元上,选择4×4高斯积分。
相对误差定义为:
(48)
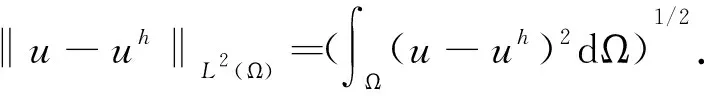
3.1 算例1
三维立方体内具有Dirichlet边界条件的Laplace方程
0(x∈Ω)
(49)
边界条件为:
u=sin(πx2)sin(πx3)(x1=0)
(50)
u=2sin(πx2)sin(πx3)(x1=1)
(51)
u=0(x2=0,x2=1,x3=0,x3=1)
(52)
其中求解域Ω=[0,1]×[0,1]×[0,1].
对应的解析解为:
(53)
将问题域Ω沿x1方向均匀地分裂为L个子域,在平面Ox2x3上节点均匀分布为10×10,即整个问题域Ω上的节点分布为(L+1)×10×10.
表1为指数型权函数在α不同时,分别对应于最佳节点分布处,DSEFG方法取得的相对误差最低和CPU运行时间的结果。图1显示了L=10,α=0.3时,指数型权函数的DSEFG方法取得的相对误差最低。

表1 以指数型权函数的DSEFG在不同参数下与相对应的节点分布取到的最低相对误差的比较Tab.1 Comparison of the lowest relative error between DSEFG with exponential weight function and corresponding node distribution under different parameters
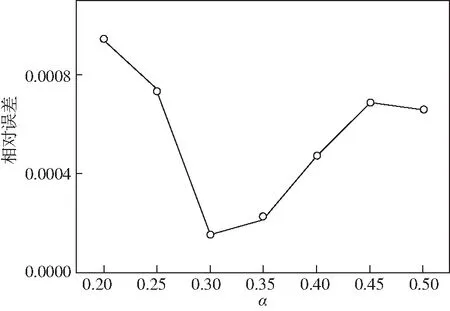
图1 指数型权函数下的DSEFG方法在α不同时的相对误差Fig.1 Relative error of DSEFG method under exponential weight function with different α
图2-图5是DSEFG方法在L不同时的相对误差。当问题域Ω分裂的子域L不同时,随着L的增加,以三次样条,四次样条为权函数时计算值逐渐收敛,以CSBRF2函数和指数型函数为权函数时计算值均是在一点处取到最低,且在以指数型函数为权函数时,DSEFG方法的计算精度最高。
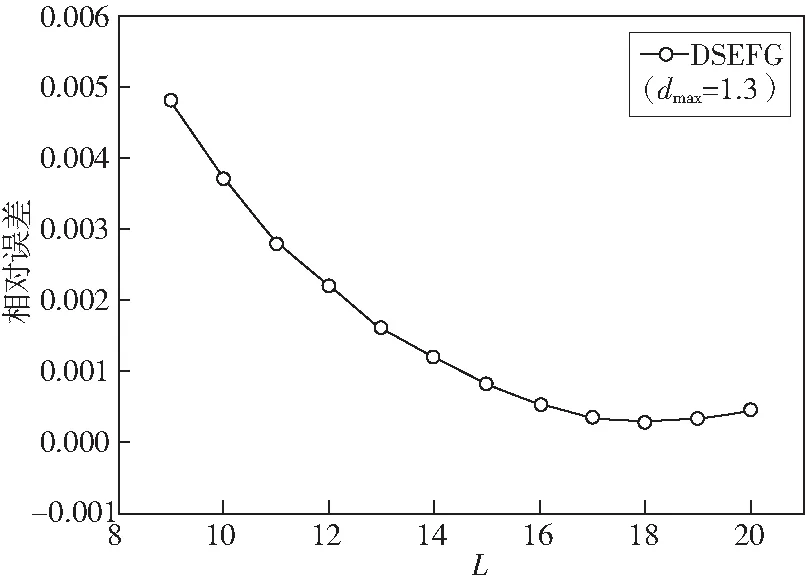
图2 三次样条函数下的相对误差与L的关系Fig.2 The relationship between relative error and L under cubic spline function

图3 四次样条函数下的相对误差与L的关系Fig.3 The relationship between relative error and L under quartic spline weight function
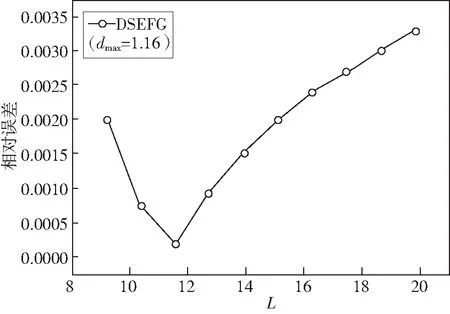
图4 CSBRF2权函数下的相对误差与L的关系Fig.4 The relationship between relative error and L under CSBRF2 weight function
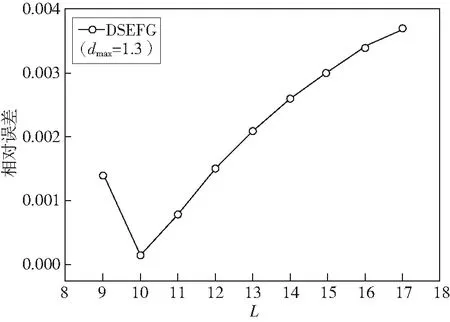
图5 指数型权函数下的相对误差与L的关系Fig.5 The relationship between relative error and L under exponential weight function
表2显示了采用不同权函数得到的最低相对误差和运行时间,且通过比较得出在以指数型函数为权函数时,维数分裂无单元Galerkin方法的计算精度和计算时间都相对较低。

表2 不同权函数下DSEFG方法的相对误差与CPU时间Tab.2 Relative error and CPU time of DSEFG method under different weight functions
图6为以不同函数为权函数时,DSEFG方法在(x1,7/9,7/9)处的值,可以看出都能很好的接近于解析解。并且在以指数型函数为权函数时,DSEFG方法的运行速度相对快一点。

图6 不同权函数下的DSEFG方法在u(x1,7/9,7/9)处的计算结果Fig.6 Calculation results of DSEFG method at u(x1,7/9,7/9) under different weight functions
3.2 算例2
三维立方体内具有Neumann边界条件的Laplace方程
∇2u(x)=0(x∈Ω)
(54)
边界条件为:
(55)
(56)
(57)
(58)
其中求解域Ω=[0,1]×[0,1]×[0,1].
对应的解析解
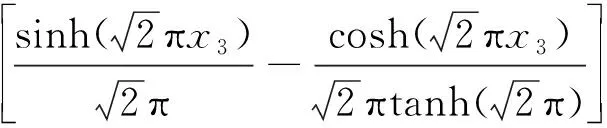
(59)
对于该问题,选取x3为分裂方向,节点分布为11×11×11,dmax=1.19.图7显示了在沿x3方向不同权函数下DSEFG方法的取值结果,都能较好的落在解析解上。表3显示了在以指数型函数为权函数时,维数分裂无单元Galerkin方法具有较好的精度,且计算速度较快。
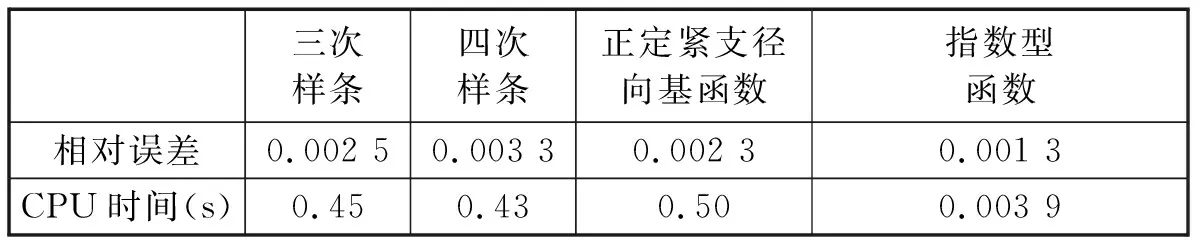
表3 不同权函数下DSEFG方法的相对误差与时间Tab.3 Relative error and time of DSEFG method under different weight functions
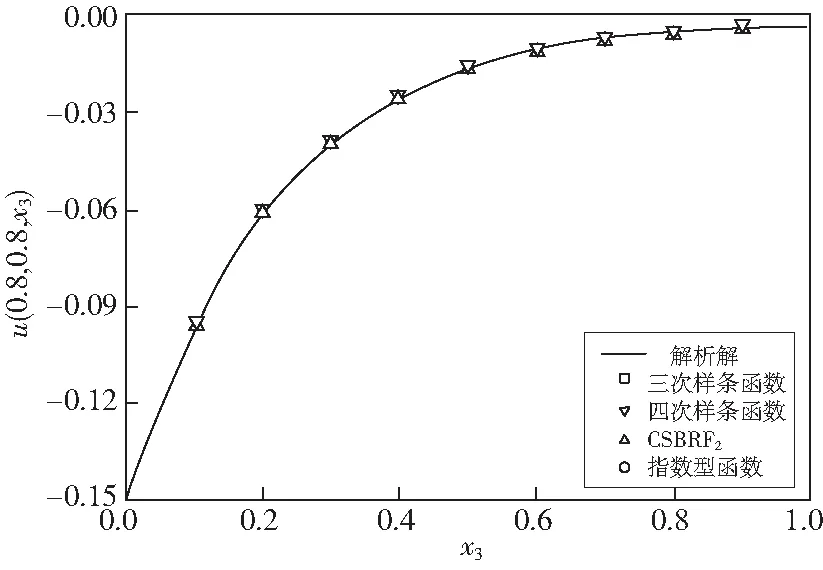
图7 不同权函数下DSEFG方法的比较结果Fig.7 Comparison results of DSEFG method under different weight functions
4 结论
本文中,通过数值算例说明了利用DSEFG方法求解三维势问题时,权函数及权函数中的参数对数值计算结果的精度和速率都有重要的影响。并且得出,求解三维Laplace方程时,权函数选择指数型函数,维数分裂无单元Galerkin方法可以得到较好的结果。
