爆破施工对地下洞室群的影响研究*
2022-09-20张春锋秦天戈李丽平
张春锋,秦天戈,张 旭,曹 正,李丽平,吴 立
(1.浙江省隧道工程集团有限公司,杭州 310030;2.中国地质大学(武汉),武汉 430074)
为了实现水资源优化配置,我国对于水利水电工程的建设正在高速发展。为满足工程需要,水利工程主厂房多采用地下洞室群的布置形式。地下厂房多布置在坚硬完整的岩体当中,地下洞室间距往往很小,钻爆法由于其工艺简单、适用范围广、成本低等优点被广泛采用,但爆破施工难免对地下洞室群的安全稳定性产生影响。
卢文波等介绍了国内主要爆破振动安全判据[1,2],指出了现有安全判据的不足,并认为峰值振动速度可以作为爆破振动安全判据。杨建华等采用数值模拟方法研究了不同地应力水平下爆破开挖诱发围岩损伤机理及爆破损伤 PPV阈值变化规律[3]。李小贝采用现场试验与数值模拟相结合的方法分析了小净距隧道爆破振动分布规律与出现的破坏形式[4],并指出了隧道迎爆侧衬砌峰值振速与围岩级别呈正相关。李兴华等采用波函数展开法[5],分析得出了地震波主频和围岩弹性模量对动应力集中系数的影响较大,泊松比影响较小。陈祥等分析了爆破振动影响下地下洞室群围岩的振动响应规律[6],确定了相邻已开挖洞室迎爆侧边墙的安全净间距。刘殿柱和于建新等对上下交叉隧道爆破振动控制进行研究[7-10],提出了振动控制标准。陈俊桦等以溪洛渡水电站地下厂房为研究背景[11],通过数值模拟和现场试验对地下洞室群进行分析,提出了考虑和初始损伤相关的岩石爆破损伤模型,确定了考虑初始损伤影响的爆破破坏影响范围的判据。李新平等通过现场试验发现地下洞室边墙爆源近区和边墙中心区域存在放大效应[12],并推导了爆破边墙PPV预测公式。罗驰等根据现场试验测出了隧道初期支护爆破振动动应变与分布规律[13],提出了一种在建隧道结构允许振速标准确定方法。
爆破振动的危害一直是国内外在隧道开挖领域中研究的重点,针对爆破振动对小净距、小跨度隧道的影响,国内外进行了大量的研究,但对于大断面地下洞室边墙新建隧道爆破对地下洞室群的影响研究相对较少。大断面地下洞室边墙放大效应较强,各洞室间距较小,爆破振动强度较大。本文以宁波至杭州湾新区引水工程溪下隧道爆破开挖为背景,通过现场爆破振动监测和数值模拟相结合的方法对近距离爆破振动影响下大断面地下洞室群的振动规律进行研究,计算得出保证地下洞室群安全爆破开挖的临界振动速度。
1 工程概况
宁波至杭州湾新区引水工程(头部工程至兴五路段)Ⅰ标,工程建设内容主要包括地下阀室、交通洞、输水隧洞、施工支洞及通风竖井。其中地下阀室位于宁波市海曙区横街镇大头岩岗山头下面。地下阀室高度为17.6 m,跨度为13.6 m,长约57 m,埋深110~125 m左右,分别与输水主洞(开挖断面3.35 m×3.2 m)、溪下水库应急衔接段(开挖断面5.45 m×4.2 m)、交通洞(开挖断面5.65 m×5.8 m)、亭下应急衔接段(开挖断面5.45 m×4.2 m)和阀-②支洞(开挖断面5 m×4.5 m)相连,洞室围岩为未风化粉砂岩,岩体较完整,岩质为坚硬岩,BQ值为529,围岩分类为Ⅱ~Ⅲ类。交通洞、阀-①、阀-②、阀-③、输水主洞以及地下阀室均已开挖完成,地下阀室洞室群平面布置图如图1所示。溪下水库应急衔接段爆破开挖,采用全断面光面爆破,炸药种类为2#岩石乳化炸药,雷管选用数码电子雷管。

图 1 地下阀室洞室群布置图(单位:m)Fig. 1 Layout of underground caverns(unit:m)
2 监测方案
2.1 振动监测方案
监测仪器选用成都中科测绘有限公司生产的TC-4850测振仪。现对亭下水库应急衔接段进行监测,监测点布置如图2所示。以输1+92.849里程断面作为监测断面,1号机固定在断面迎爆侧边墙距底板约1.5 m处,2号机固定在靠近背爆侧底板,3号机固定在背爆侧边墙距底板约1.5 m处。

图 2 测点布置图(单位:m)Fig. 2 Layout of measuring points(unit:m)
固定传感器时,在较为平整坚硬的洞壁上使用电钻打孔,使用石膏粉加水搅拌将传感器与岩体表面连接起来,使用钢筋和铁丝将传感器固定,使其可与洞壁一同振动。安装传感器时将传感器X、Y方向设为水平方向,其中X方向平行于洞室轴线,Y方向垂直于洞室轴线,Z方向为竖直方向。底板的传感器布置时应选在较为水平的裸露岩石上,使用石膏使其与底板固定,X方向指向爆源,Y方向与X方向保持垂直,Z方向为竖直方向。现场测点布置如图3所示。

图 3 现场测点布置Fig. 3 In-situ layout of monitoring points
2.2 监测数据分析
现场进行爆破振动测试,爆破工作面里程桩号为输1+126,该断面距离地下阀室水平距离约9.0 m。获取了亭下应急衔接段隧道各测点的监测数据,包括径向(X方向)、纵向(Y方向)、垂向(Z方向)三矢量方向及合成矢量振动速度。典型振动速度时程曲线如图4所示。爆破振动测试数据见表1。
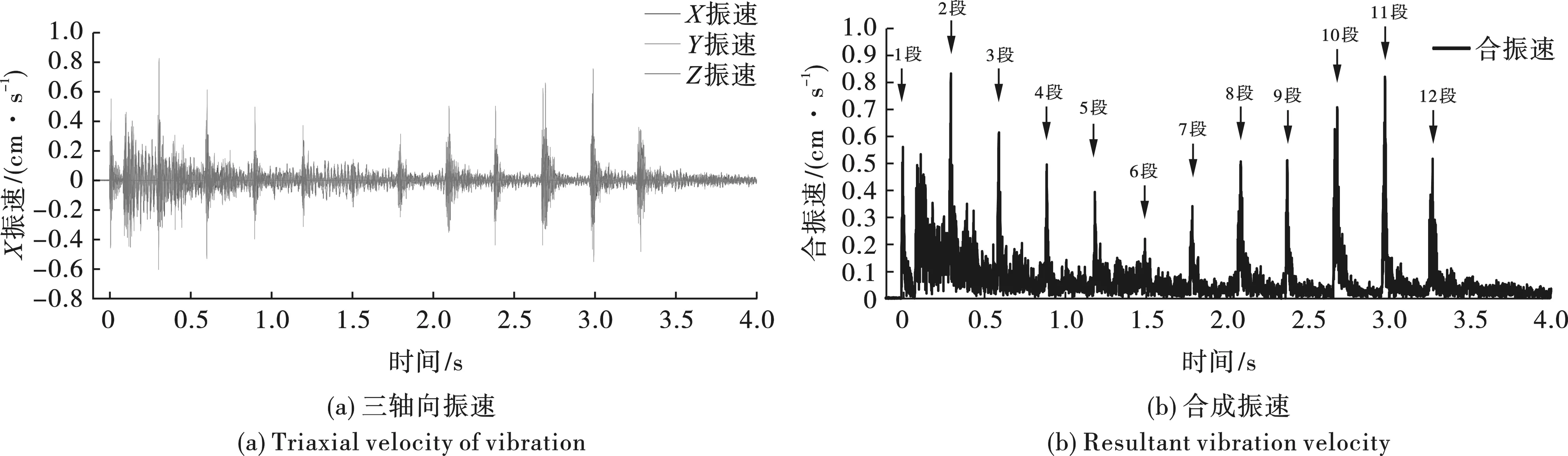
图 4 典型实测速度时程曲线Fig. 4 Typical measured velocity-time curves

表 1 各监测点的峰值振速
如图所示,振动速度最大值为掏槽段,单段药量为9.6 kg。在洞室围岩不同位置的振速有所不同,位于迎爆侧洞壁Y向振动速度最大,Z向次之,X向最小;背爆侧洞壁振动速度则Z向最大,X向次之,Y向最小。因此要将爆破振动控制的重点主要放在掏槽爆破段。
3 数值模拟与分析
3.1 计算模型
为研究地下洞室爆破开挖邻近主洞室的动力响应特征,根据地下阀室与各隧道的空间位置关系,建立地下阀室、溪下水库应急衔接段、亭下水库应急衔接段和阀②支洞的三维数值模型,模型区域见图1红框。将掌子面设置在溪下隧道输1+126断面,该断面距离地下阀室水平距离约9.0 m,爆破开挖段(一个爆破进尺)3 m,仅考虑最大单段药量为9.6 kg段别炸药起爆。
数值计算模型如图5所示,模型三维尺寸为73.6 m×79 m×69 m,X方向与地下阀室轴线水平方向垂直,Y方向为竖直方向,Z方向平行于地下阀室轴线方向。

图 5 数值计算模型(单位:m)Fig. 5 Numerical calculation model(unit:m)
为了避免边界效应,考虑在地下阀室侧向岩体取三倍洞跨,上部岩体取三倍洞高。地下阀室设计埋深约为110~125 m,为简化模型对上覆岩体考虑深度为120 m。数值模型采用cm-g-μs单位制。
3.2 材料参数
围岩和炸药采用Solid-164单元,围岩采用Lagrange算法,炸药使用ALE算法,通过多物质流固耦合方式(*CONSTRAINED_LAGRANGE_IN_SOLID)来处理围岩和炸药之间的相互作用,用这种算法可以解决大变形引起的炸药单元严重畸变的问题。岩体的本构模型采用双线性随动硬化模型*MAT_PLASTIC_KINEMATIC来定义,本构关系如式(1)所示
(1)
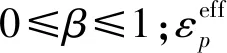
岩体的物理力学参数根据勘察报告设计参数建议值结合多组现场实测数据调整确定,岩体主要材料参数如表2所示。
炸药的材料模型选用LS-DYNA中的*MAT_HIGH_EXPLOSIVE_BURN来定义,爆轰压力P用JWL状态方程来描述,如式(2)所示
(2)
式中:A、B为炸药材料的相关参数;R1、R2、ω为炸药材料的相关常数;V为初始相对体积;E为初始内能。
2#岩石乳化炸药的主要材料参数如表3所示。

表 2 岩体参数

表 3 炸药参数
3.3 亭下隧道振动响应分析
模型中与监测点1(爆心距24.67 m)、监测点3(爆心距26.66 m)对应的节点46926、46723合成振动速度曲线如图6所示。现场监测数据迎爆侧最大振动速度为5.1948 cm/s,背爆测最大振动速度为0.8329 cm/s。数值模拟计算结果迎爆侧最大振动速度为5.5919 cm/s,比实测结果高7.6%;背爆侧最大振动速度为0.8799 cm/s,比实测结果高5.6%。总体而言数值结果与现场试验结果吻合较好,模拟值普遍略大于实测值,计算模型可靠。
为研究亭下隧道受爆破振动作用的影响规律,选取亭下隧道合成振动速度与最大主应力最大的横截面记作截面A,截面桩号为输1+102.818。在截面A取若干个测点,表示相应部位的振速、最大主应力。亭下隧道横截面A合成振动速度和最大主应力分布图如图7所示,其中右侧为迎爆侧。

图 6 测点合成振动速度时程曲线Fig. 6 Simulated velocity-time curves
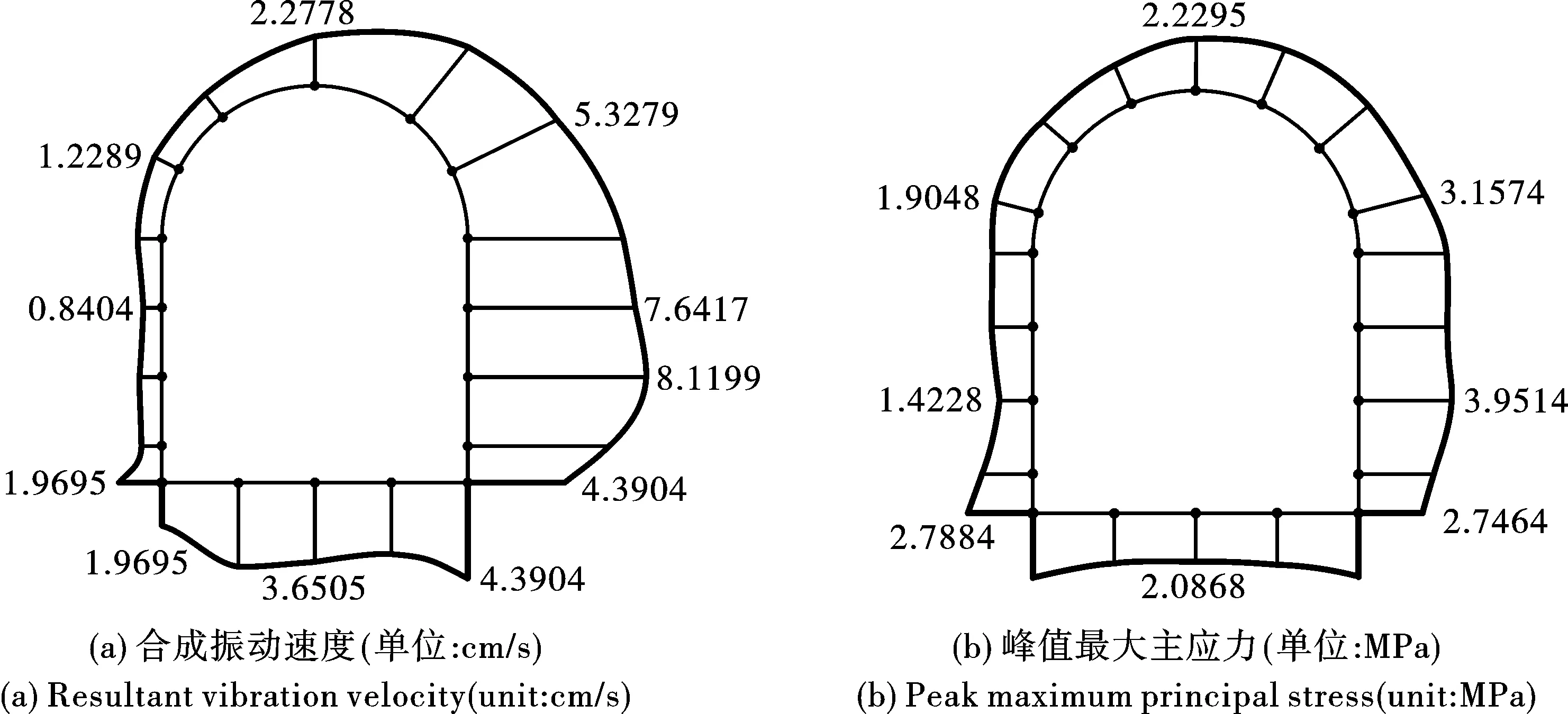
图 7 亭下隧道围岩振动速度与最大主应力分布图Fig. 7 Distribution of peak vibration velocity and peak maximum principal stress of surrounding rock of Tingxia Tunnel
对计算结果分析可知,振动速度与最大主应力最大的位置均位于迎爆侧墙腰附近,距离底板约1.5 m;迎爆侧峰值振动速度约为背爆侧峰值振动速度的3.3~9.0倍,迎爆侧峰值最大主应力约为背爆侧峰值最大主应力的1.4~2.8倍;最大主应力的正负值代表围岩的不同应力状态,此处正值为拉应力,负值为压应力。各测点最大主应力峰值均为正值,说明洞室围岩在爆破作用下受到的拉应力更大。由于岩石的抗拉强度远远小于抗压强度,因此爆破振动对于地下洞室群围岩的影响主要以拉破坏为主。
3.4 地下阀室振动响应分析
溪下隧道自地下阀室边墙爆破开挖,由计算结果可知,峰值振动速度与最大主应力最大的区域位于溪下隧道与地下阀室相接的洞壁,取该洞壁(阀室桩号FSZ0+052)为截面B,对该截面按间距3.0 m取若干个监测点,测点布置图如图8所示,各监测点数据如表4所示。

图 8 地下阀室测点布置图(单位:m)Fig. 8 Layout of monitoring points of underground chamber(unit:m)
根据计算结果可知,地下阀室洞壁最大峰值振动速度为27.1 cm/s,最大拉应力为1.6 MPa;在洞壁与溪下隧道交界面附近的峰值振动速度和拉应力显著大于其他区域,容易出现张拉破坏;峰值振动速度与最大拉应力随着爆心距的增加衰减规律相近。该截面是地下阀室受爆破振动作用影响最大的截面,需重点关注。

表 4 测点振动速度与最大主应力
为探究地下阀室轴线方向受爆破振动影响规律,取阀室桩号FSZ0+051为横截面C,截面C峰值振动速度与最大主应力分布图如图9所示。

图 9 地下阀室围岩振动速度与最大主应力分布图Fig. 9 Distribution of peak vibration velocity and peak maximum principal stress of surrounding rock of underground chamber
由于溪下隧道位于截面C的左下方,所以振动速度与最大主应力的最大值区域出现爆源近区,墙腰的振动速度与最大主应力略小于底板,处于相同水平。位于截面右侧围岩墙腰处振速明显增大,但最大主应力却有所减小,可能是由于该区域正好处于亭下隧道与地下阀室交接的墙角,受到围岩的夹制作用较小,对振动速度有放大效应。
沿地下阀室轴线方向每隔10 m取一横截面,提取墙腰与底板处的峰值振动速度与最大主应力来分析地下阀室轴向规律,结果如表5所示。
由计算结果可以看出,地下阀室墙腰与底板位置的峰值振动速度与最大主应力沿轴线方向衰减规律相近;在60.06 m处墙腰位置的振动速度与最大主应力显著降低,幅度明显大于底板位置,这是由于该点位于输水主洞的背爆侧,已开挖洞室具有较为明显的减振效应。

表 5 测点振动速度与最大主应力轴向分布
4 相邻洞室安全判据
综合前面对爆破作用下邻近洞室振动速度、应力分布规律的讨论,地下阀室的迎爆侧洞壁是最容易出现破坏的危险部位。在对邻近洞室安全稳定性分析时,可以以已开挖洞室迎爆侧洞壁峰值振动速度为判断指标。对表5中的峰值振动速度与峰值拉应力数据进行拟合,建立函数模型,如图10所示。
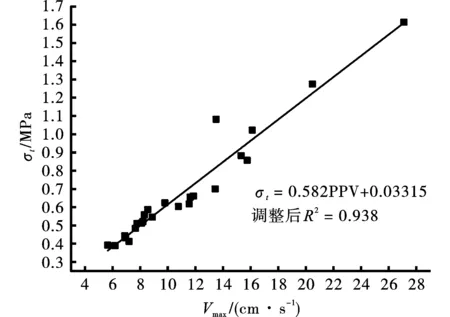
图 10 地下阀室洞壁最大拉应力与峰值振动速度统计关系Fig. 10 Statistical relationship between maximum tensile stress and maximum vibration velocity of underground chamber
由图10可知,在爆破振动的作用下,邻近地下阀室最大拉应力与峰值振动速度间统计关系拟合曲线方程为
σt=0.0582Vmax+0.03315
(3)
根据最大拉应力准则,当围岩所受最大拉应力大于极限抗拉强度时,会引起材料脆性断裂破坏。极限抗拉强度对应的峰值振动速度可以作为爆破振动安全判据。已知地下阀室围岩较完整,静抗拉强度为2.70 MPa,由于岩石动抗拉强度稍大于静抗拉强度,此处用静抗拉强度代替动抗拉强度,带入式(3)计算可得,邻近地下阀室Vmax=45.82 cm/s;当以峰值振动速度作为判断指标时,邻近地下阀室围岩发生破坏的临近振动速度为45.82 cm/s。
5 结论
本文通过对溪下应急衔接段隧道爆破施工过程进行现场爆破振动监测,建立地下洞室群模型进行数值模拟计算,讨论了爆破振动对邻近隧道、大断面地下阀室的影响。通过对现场实测数据和计算结果的对比,该模型较为可靠,对类似的工程具有一定的指导意义。主要研究结论如下:
(1)邻近洞室迎爆侧峰值振动速度与最大拉应力均大于背爆侧,是影响围岩稳定性的主要部位,洞室围岩在爆破振动作用下受到的拉应力更大。
(2)在大断面地下阀室边墙新建小断面隧道时,综合峰值振动速度、最大拉应力准则考虑,爆破开挖的地下洞室边墙最容易发生拉伸破坏,爆源近区的地下洞室边墙和底板也需要注意。
(3)根据数值模拟结果确立了极限拉应力判据,得出了最危险部位地下阀室与溪下隧道相接洞壁围岩发生破坏的临界振动速度为45.82 cm/s。
