组合静载条件下SHPB试件长径比优选研究*

2022-09-20汪旭光郭连军徐振洋闫大洋

爆破 2022年3期

潘博，汪旭光，郭连军，徐振洋，闫大洋

(1.北京科技大学土木与资源工程学院，北京 100083；2.辽宁科技大学矿业工程学院，鞍山 114051；3.沈阳工业大学建筑与土木工程学院，沈阳 110870；4.鞍钢矿业爆破有限公司，鞍山 114046)

采空区是常见的矿山事故隐患之一，其失稳引发的后果严重影响生产循环效率，甚至危及人员设备安全，有别于地下采空区，露天矿山既有采空区围岩体受到的地应力作用较小，处理方式多以爆破崩落为主，因此掌握这类采空区围岩体的动力学性质，对爆破方案的优化有着重要的意义。SHPB作为常用的研究动力学性质试验装置，在岩石类材料领域的得到了广泛的应用，如冲击荷载作用下岩石的动态破坏过程及损伤演化规律[1,2]，循环冲击荷载作用下力学性质[3-5]，以及温度对岩石力学性质的影响等[6]。随着技术的发展，众学者又开展了压力伺服以及三轴动态压缩试验[7,8]。通常试验结果与试件的长径比有关，ISRM(International Society for Rock Mechanics and Rock Engineering)给出了长径比建议范围，不同岩种的长径比对结果影响如何，众学者进行了研究：花岗岩的弹性变形模量与试件长径比呈正相关[9]，而试件最终破坏模式同样与长径比相关[10]；煤的峰值应变随着试件长径比的增加呈指数衰减[11]；石灰岩的峰值应力应随着试件长径比增加而减小，而动态模量则先增后减[12]。如何确定试件的最佳长径比，也是研究热点：对于大直径SHPB试验，研究发现当长径比为0.4～1.0时试验结果能够较为真实的反应出材料性质[13]，刘殿书等研究结果显示[14]，长径比为0.67时为最优，并给出了长径比取值范围为0.6～1.0；梁书锋等从应力波在试件中传播角度[15]，给出了部分脆性岩石长径比参考值为0.7～0.8；宫凤强等给出了应力波在试件中传播次数查值表[16]，并基于岩石波速给出了试件尺寸计算关系。

综上可知，长径比对试验结果有直接影响，但上述研究给出的最佳比均是在无轴压、无围压的试验条件下分析得出，这显然与岩体实际赋存环境不符，而对于轴压、围压伺服条件下，选用何种长径比的试件进行SHPB试验，获取更为准确的岩石动力学性质，还未见相关报道。因此，本文将以鞍钢矿山采空区岩样为例，开展静载组合条件下不同长径比试件SHPB试验，通过分析试件在轴压及围压伺服下对冲击荷载的响应情况，得出试件应力平衡状态、动态力学特征，确定试验条件下试件的最优长径比，并与无静载组合伺服条件下的试验所得最佳长径比结果进行对比，以说明研究的必要性，进而为后续获取可靠的围岩动力学性质奠定基础，同时也为相关研究中试件长径的优选提供参考。

1 试验装置及方案

1.1 试验装置及试件制备

试验采用自制50 mm分离式霍普金森压杆(SHPB)实验系统，如图1所示。试验装置包括电磁控制系统、动力系统、液压轴压及侧向围压伺服系统、冲击弹体、入射杆、透射杆、吸收杆及数据采集系统。其中入射杆长为2100 mm、透射杆长为1800 mm，吸收杆长度为800 mm，材质均为C50高强度钢，弹性模量为210 GPa。

图 1 分离式霍普金森压杆实物图Fig. 1 Split Hopkinson pressure bar system

本次试验试件取自鞍钢矿业齐大山铁矿-150 m 水平既有采空区围岩体，岩性以混合花岗岩为主，基本力学参数见表1，对岩芯进行加工处理，保证两端面平整度符合ISRM要求，试件直径为50 mm，根据相关研究成果[16]，制备长径比为0.6、0.8、1.0、1.2、1.4的试件，成品如图2所示。

表 1 采空区围岩基本力学参数

图 2 试验试件Fig. 2 Test specimen

1.2 试验方案

结合实际围岩的赋存情况，参照文献[17]采用低侧向围压(4 MPa)，4 MPa轴向压力，对五种长径比试件进行冲击作用。由于试件受围压及轴向压力约束，同时可实现装置系统的单脉冲加载的动能陷阱技术[18]，即弹头撞击入射杆产生的应力波作用于试件，削减了杆件的相对运动带来的二次冲击作用，试件不易被冲破，因此，结合现场爆破作用应变率情况，采用0.5 MPa冲击作用气压进行试验。

2 试验数据分析

2.1 应力平衡分析

使用SHPB获取岩石的本构特征的前提是，有效获取被测岩石试件处于应力平衡状态时的数据，那么试件两端的应力平衡状态维持时间的长短则决定是否可以获取足够多的有效数据，岩石类材料的应变通常处于10-3～10-2量级(如图3)，加之岩石材料各向异性的特点，导致在相同冲击荷载条件下试件发生不均匀形变。试件长径比的改变将直接影响应力波在试件内的单程传播时间，进而对应力平衡过程的持续时间产生影响。引入应力平衡因子(记作η)，即试件在某一时刻两端的应力幅值之比，该比值越接近于1，则认为试件两端应力越接近于平衡状态，那么当η=1时，则认为试件两端应力达到平衡状态[19]。

(1)

式中，σT、σI、σR分别为试件透射端透射应力及入射端入射应力和反射应力。

基于此，在试件加载过程中，则可通过应力平衡因子来描述试件的两端应力平衡情况，将η=1±0.1视作应力平衡，如图4所示，在冲击荷载作用初期，0～23 μs区域，应力状态逐渐由波动趋于平衡，这是由于初始阶段试件两端应力差值过大致使试件内部应力无法均匀化，所以应力平衡因子曲线呈现出明显的波动；23 μs后，各长径比试件两端逐渐达到应力平衡状态，保持了一定时长的应力均匀化，且最短准平衡时长维持了近120 μs，为充分获取数值提供了基础；175 μs后，各长径比试件的平衡因子曲线再次波动，试件无法继续保持平衡状态。

图 3 应变时程曲线Fig. 3 Strain time history curve

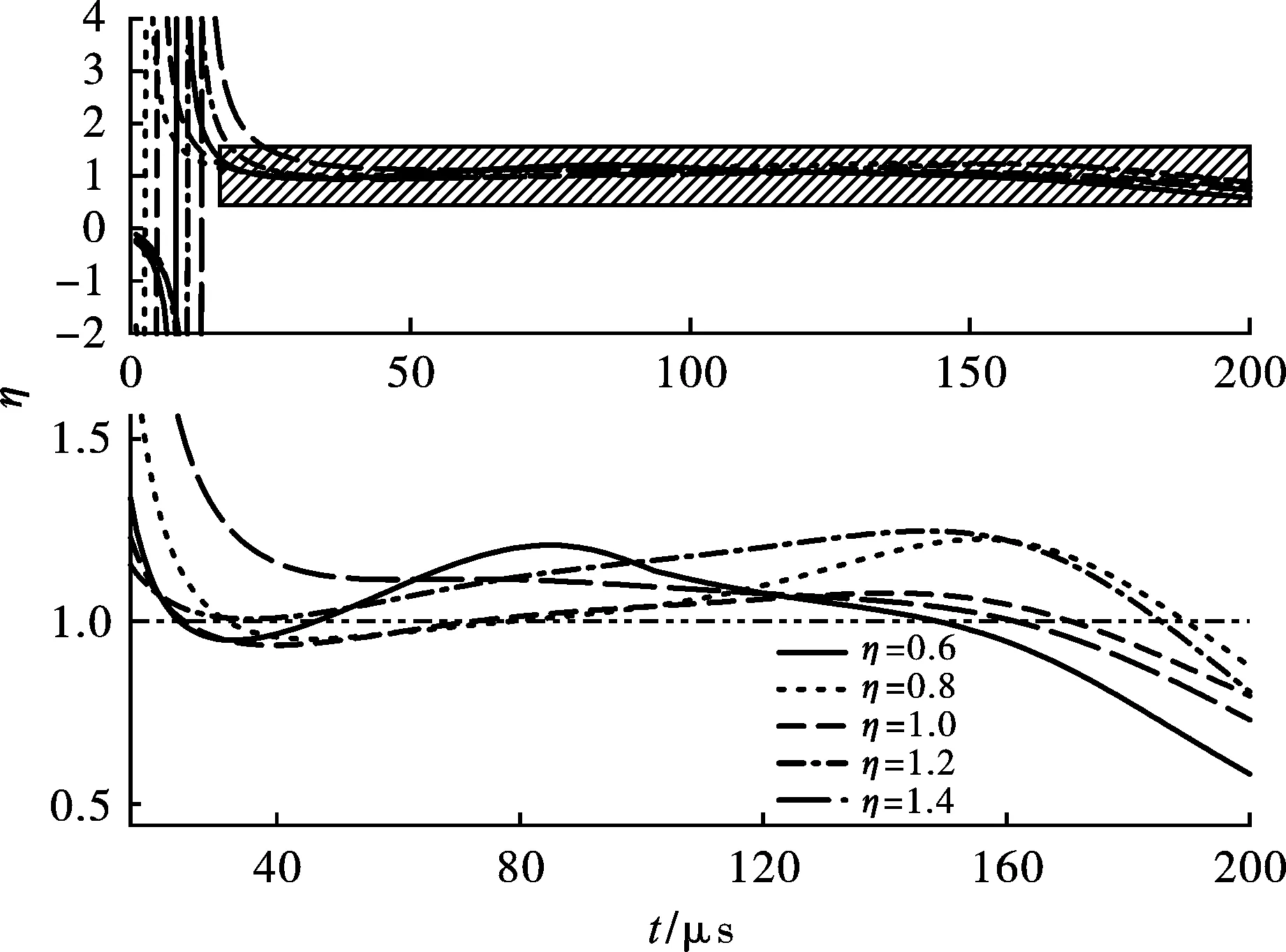
图 4 应力平衡因子时程变化曲线Fig. 4 Stress balance factor time history curve

通过各长径比试件应力平衡因子曲线变化可知，同等加载条件下试件长径比的改变，试件两端达到应力平衡状态的时间随之变化，且应力平衡阶段持续时间不同。长径比为0.6的试件，达成应力平衡状的耗时最短，但后程出现一定幅度的状态波动。长径比为1.0的试件，应力平衡状态维持时间最长，且持续时程中波动较小。当试件长径比为0.8时，试件虽然较早的达到了平衡状态，但维持时间较短，这说明合适的长径比对试件维持较好的应力平衡状态有一定的帮助。因为试件在整个过程中均未与压杆分离，应力平衡状态的达成是应力波在试件内几经反射的结果，如图5所示，长径比的差异导致了应力波在试件内单程传播时间不同，小长径比的试件单程传播时间小于大长径比试件，小长径比试件可在较短时间内实现应力平衡。

图 5 应力波传播历时影响因素Fig. 5 Influence factors of stress wave propagation duration

由于SHPB的试验原理是遵循一维应力波假设，依前文所述应力波在试件内经过几次透反射后试件可近似视为应力平衡，故入射应力σI、反射应力σR和透射应力σT之间存在如下关系[19]

σR(t)=λσI(t)

(2)

σT(t)=(1+λ)σI(t)

(3)

λ=(ρsCs-ρeCe)/(ρsCs+ρeCe)

(4)

式中：λ为应力波由入射杆传入试件的反射系数；ρs、Cs分别为试件弹性杆密度和弹性波速；ρe、Ce分别为系统杆件的密度和弹性波速。

透反射系数是由被测试材料类型决定(本文试验研究对象该系数为-0.58～-0.51)，所以在揭示不同类型试件的应力平衡问题时，需要明确在延续时间内，入射波在试件内的透、反射次数与试件尺寸之间关系，具体分析试件两端的应力差值情况。

2.2 应力差相对值

图6为实测不同长径比试件的应力时程曲线，可以看出在相同冲击荷载作用下五种长径比围岩试件入射波时程曲线特征基本相同，均为近似的矩形波。且应力波作用时间t约为250 μs，应力加载峰值点在125 μs左右。

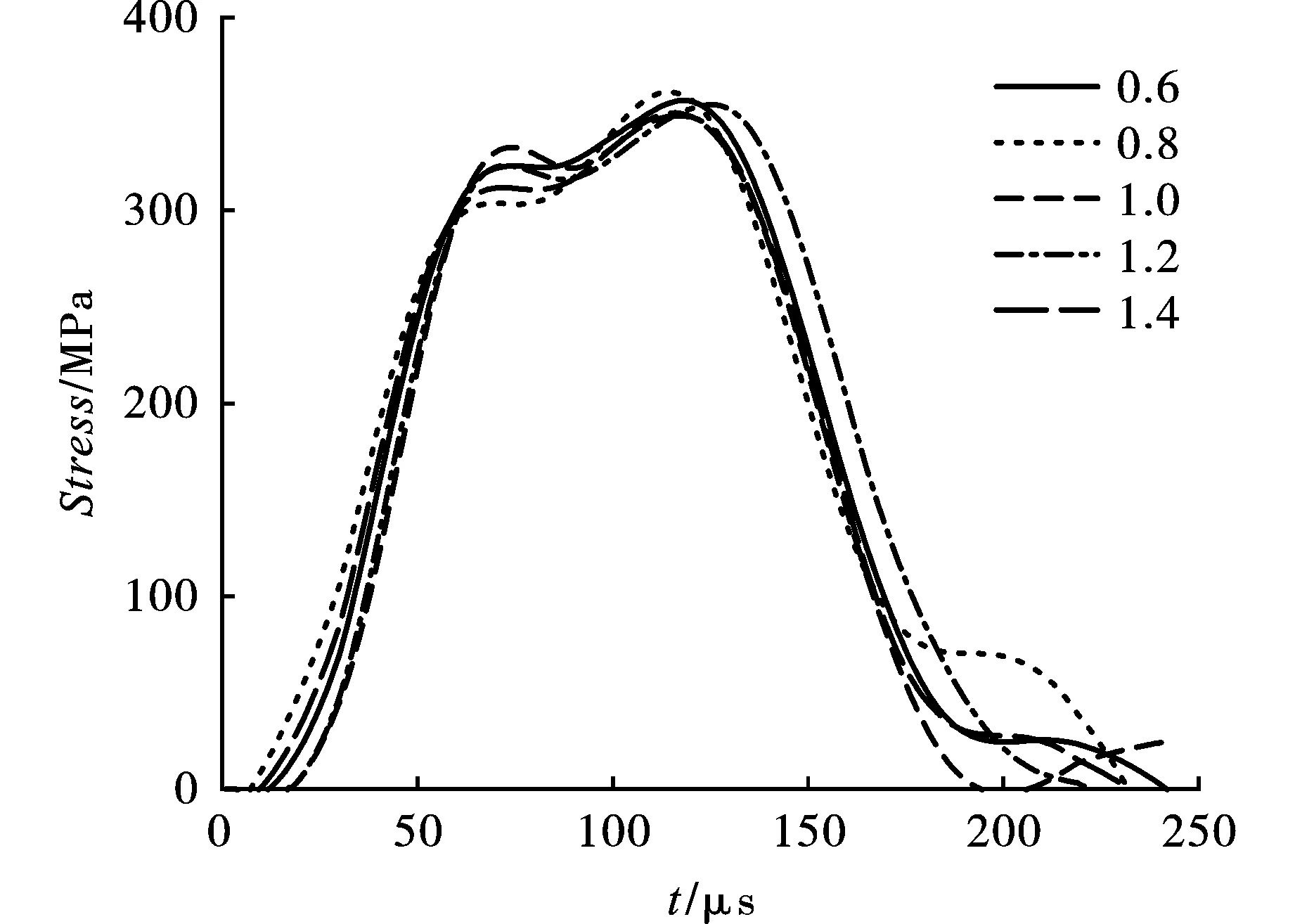
图 6 入射应力时程曲线Fig. 6 Incident stress time history curve

在应力波入射延续时间内，为提取数据并获得试件真实动态响应特征，需要明确应力波在试件内的单程历时，可由式(5)进行计算。

(5)

式中：Δ为应力波单程历时；Ls为试件长度；Cs为试件的弹性波波速。

那么可将应力波初峰段作用时间t内，在试件内传播次数记作k，则有

(6)

应力波经过反射后，在试件两端的应力差值就变的很小，当应力差值在1%时，可视为应力应变逐渐开始达到平衡，引入试件两端应力差相对值

Δσk=|σ2k+1-σ2k|

(7)

(8)

(9)

式中：Δσk为被测试件两端应力差绝对值；σk为第k次反射应力值；αk为试件两端相对应力差值。

由上式可知，应力差相对值与作用于试件两端应力平均值有关，由于试件与压杆之间的波阻抗不同，即受反射系数λ影响应力波无法全反射，随着反射次数的增加应力差相对值αk将发生变化。

2.3 试件准均匀态分析

为探讨试件的长径比差异对应力状态的影响，需对应力脉冲时间内不同长径比试件两端的应力情况进行计算。根据研究成果，可设定某一限值来描述试件的均匀状态[20]，该界限值通常需要根据不同的试验材料进行调整，因此定义当试件两端应力差相对值αk≤ 6%时，视作试件内部应力达到准均匀态，基于6%的统计结果对本文试验结果进行分析。

图7为不同长径比试件在相同冲击荷载作用下的应力差相对值αk情况。如图7(a)所示，长径比为0.6的试件，可视为在第7次达到应力近似平衡，应力差相对值αk满足了设定的界限小于6%，随着反射次数的增加逐渐减小；第10～11次时αk值达到最小值，此后试件两端的应力差相对值出现小幅增加，当反射次数达到第13～14次时αk值再次临界6%，至此试件应力状态视做平衡态。14次以后，试件两端的应力差值逐渐增加但增加幅度略有差异，其中相近的两次反射，αk最大涨幅达17%试件无法继续保持平衡状态。

图7(b)中长径比为0.8的试件应力波的反射次数关系与0.6长径比试件相比有所减小。初始阶段试件处于应力失衡状态，至应力波传播反射至8次时，试件内部首次达到应力均匀。而后αk继续小幅下降到最小值，再回落至6%以内，此后在界限值附近波动。反射至第14次后，试件相对值超出基准值，可近似认为在应力波反射第7次至13次的时间内，试件保持了平衡状态，而后αk开始上涨，试件内部的均匀化被完全打破。

由图7(c)中可看出，试件内部首次达到应力均匀需要的应力波反射次数在8～9次，当试件在应力波反射至第8次基本满足αk< 6%，其中个别试件需在反射第9次时实现近似均匀。至应力波反射第15次试件保持了较好的应力均匀。当应力波反射超过15次后，个别试件无法继续保持内部的应力均匀化状态，至第16次后所有试件的应力差相对值αk均超出界限值，个别试件涨幅达到14%，无法再保持内部应力均匀状态。

图7(d)为长径比1.2的试件数据曲线，应力波在试件内部反射至第8次时，除个别试件外，基本达到应力内部均匀，在此后的反射过程中αk呈先减小再增的变化趋势，至第12次时处于界限值6%内。当应力波反射至第13次时，个别试件内部应力突破失衡临时值，当反射次数至14次时，所测试件两端的应力差相对值均超出界限值，随后该指标持续增加，试件内部已无法重新达成应力均匀。同样，由图7(e)可以看出，长径比为1.4的试件，在监测范围(αk= 0～40%)内，反射作用第8次时，个别试件实现内部应力均匀，随后αk值均在界限值变化。当反射至第9次时，所有试件均实现准应力均匀状态，并保持至应力波反射至第12次，而后超出6%。

3 动态力学指标分析

3.1 应力-应变曲线

基于应力均匀性及一维应力波两个假设，将SHPB试验采集到的电信号依式(10)进行处理[21]，即可得到被测试件的平均应力σs及平均应变εs，进而绘制试件的动态应力-应变曲线。

(10)

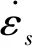
在0.5 MPa冲击气压及4 MPa轴向和4 MPa侧向压力伺服条件下，试件的长径比差异对动荷载响应表现明显的不同。如图8所示，为试验获取的5种长径比试件应力-应变曲线。由于试验装置的冲击弹头为圆柱体且冲击动能较大，因此即使经过整形片滤波作用，P-C振荡对曲线的影响仍然存在[22]，各长径比试件对应的曲线变化趋势存在明显的“双峰一谷”现象。图中可以看出，长径比影响了试件弹性变形，试件的弹性变形结束时刻应变处于0.001～0.002之间。由图3可知，不同长径比试件达到该应变值的时间基本一致，均为50 μs左右，说明加载应力波输入的稳定性，而随着长径比的增加，曲线弹性阶段的斜率逐渐增加。当试件弹性变形结束后，曲线出现了下凹发展，随后光滑上升达到曲线峰值点。可以看出，长径比不同峰值应力点的差值相差不大，处于350～360 MPa范围内，由于试件的宏观损伤较小，因长径比而产生的尺寸效应对峰值应力的影响处于较低的水平。当曲线经过动态应力峰值点后，开始光滑下降，长径比为0.8～1.2的试件曲线至阶段最大应变点处开始呈闭口收缩，至动态强度达到100 MPa附近，曲线再次呈开口发展趋势。而长径比为0.6及1.4的试件则表现出了应变缓慢增加一定值后，同样存在驻点使得曲线的应变增加变快。

由上述描述可知，如果不考虑设备本身的误差影响，即加载波的能量恒定，那么长径比的差异对动荷载的响应，主要表现在峰值点的应变大小以及曲线的整体开口程度。有研究指出曲线与应变轴所围的面积是冲击加载过程中的耗散能[23]，那么可知试件的长径比越小同等条件下能消耗更多的能量。如图中显示长径比为0.8时面积略小，在1.0～1.4范围内时所围面积基本相等。受此启发，在工程实际中应充分考虑每个炮孔爆炸能量破岩作用范围，进而确定孔网参数，爆炸能量充分利用的同时，最大限度的减小炸药消耗而产生的碳排放。

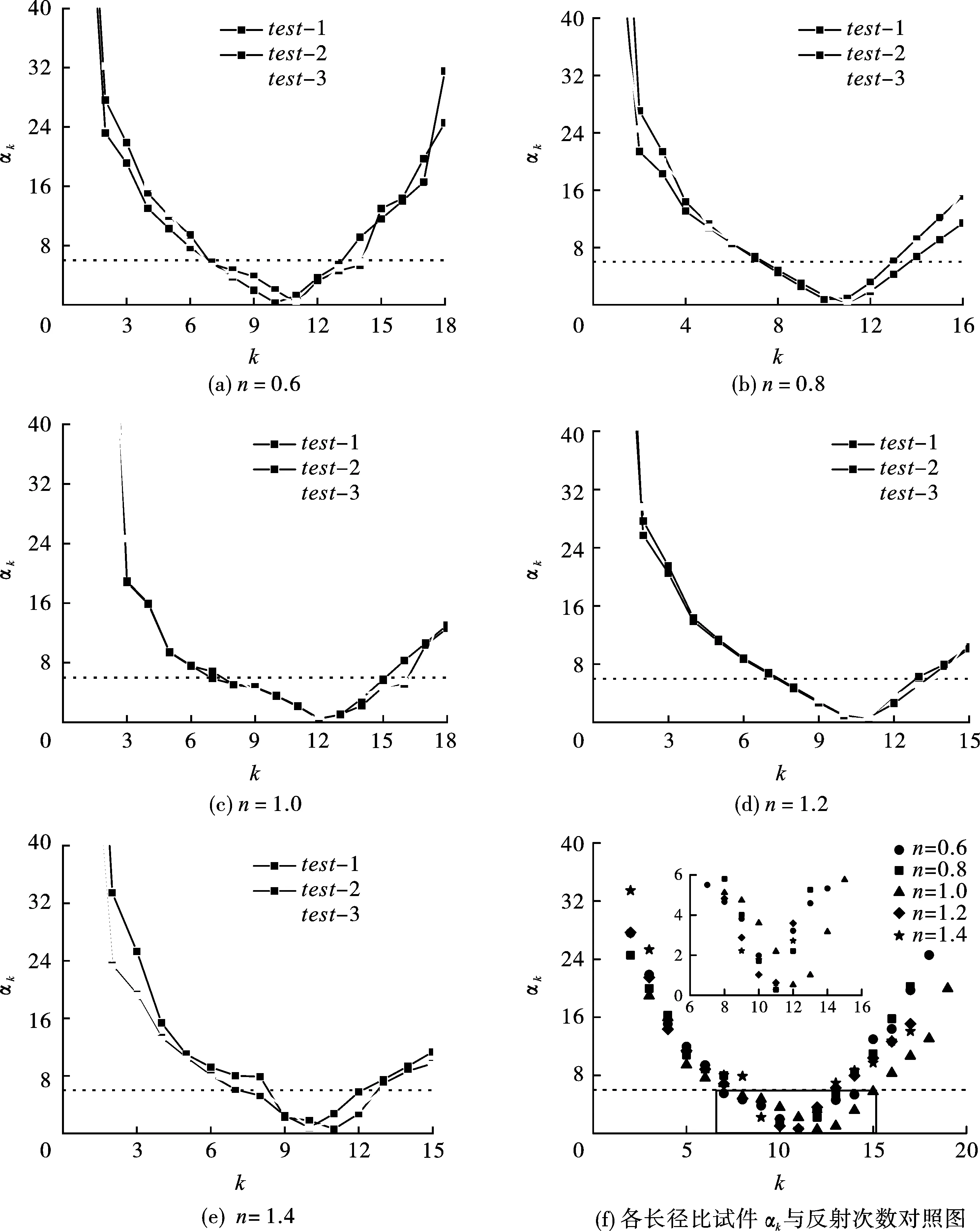
图 7 应力差值相对值与传播次数关系曲线Fig. 7 Relation between relative value of stress difference and propagation times

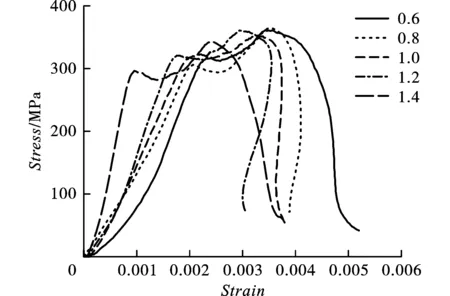
图 8 不同长径比围岩试件应变-应力曲线Fig. 8 Strain-stress curves of surrounding rock specimens with different length-diameter ratios

3.2 峰值强度分析

图9为不同长径比试件测试所得峰值强度结果，可以看出除长径比0.8的试件离散程度较大外，其余试件所测得的结果离散程度较小。造成离散的原因一是试件本身的差异，由于试件较为致密，虽然试验前已采用NMR(Nuclear Magnetic Resonance)技术进行差异化排除，但只能通过孔隙情况加以剔除，无法完成知晓内部潜在的结构特点或其他强度较为突出的成分含量；二是试验设备触发异常导致子弹的入射动能量发生变化，使得测试结果显示出小幅增加。通过试验结果的平均值可以看出，5种长径比的试件均处于360 MPa附近，最小为n=1.0试件的354.12 MPa，最大为n=0.8试件的367.42 MPa，随着长径比的增加峰值强度呈现小幅波动。

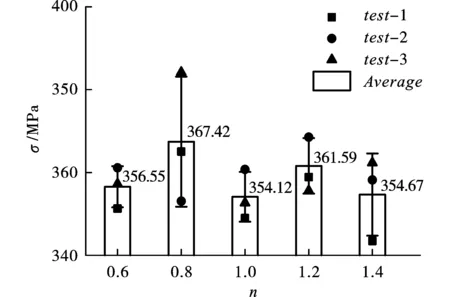
图 9 峰值强度分布Fig. 9 Peak intensity distribution

3.3 峰值点割线模量分析

由于试验过程中，试件并未发生破坏宏观的破坏，峰值应力值只能从一定程度上反应试件的动态强度，且应力-应变曲线中的应变在回弹后有再次增加的趋势，定量表征不同长径比的试件的变形性质略显不足。引入割线模量可以就试件弹性变形至极限强度的过程，对材料的塑性变形情况进行直观的描述。由图10可知，长径比的差异对峰值点割线模量的影响更为明显，长径比为1.0的试件数据离散程度最小，其余长径比试件离散程度均明显大于长径比1.0的试件结果。应力峰值点的割线模量峰值随着长径比的增加呈准线性增加趋势，当长径为1.2时该指标较0.6至1.0的增幅相对放缓，当长径比增至1.4时，动态峰值点割线模量大幅增加，均值为183.2 GPa，由此可知，随着长径比的增加，试件在相同冲击荷载作用下的塑性变形演化速率有所增加。离散程度的大小说明了重复试验的稳定性，即长径比为1.0的试件，自弹性阶段后产生塑性变形开始至屈服的过程相对较为稳定，这为后续其他组合形式的冲击荷载试验选定试件长径比提供了依据。

图 10 动态峰值应力点割线模量分布Fig. 10 Secant modulus distribution of dynamic peak stress points

4 讨论

由应力平衡差值分析可知，随着试件长径比的增加，试件达到准平衡状态应力波在试件内的反射次数有所增加，由长径比0.6的第7次增加至第9次完全平衡。但试件两端应力差相对值满足限定值的次数，并不是按比例递减，在相同冲击冲击荷载作用下，长径比为1.0的试件满足αk< 6%的次数最多，这与应力平衡因子曲线结果一致，且应力差相对值与传播次数关系曲线与文献[16]中描述基本吻合。对不同长径比试件αk与反射次进行统计，各尺寸试件满足基准值的次数依次为：8次、7次、9次、6次和5次。达到基准值的次数越多，则说明试件内部的应力均匀性情况越好，同等条件下得到的试验结果更为可靠，以前文中的峰值点割线模量为例，长径比为1.0的试件数据离散程度明显小于其他组别，而试件长径比为1.4的数据离散程度最大。

同组别试件初次实现应力平衡出现差异性，一是由于岩石本身的各向异性及非连续性特点，随着应力波在岩石内部传播反射，将进一步使岩石的内部结构发生变化，因此随着传播次数的增加，试件两端的应力差相对值必将呈现出一定的波动，内部形成新的稳定结构有前后时差。二是应力波在传播过程中强度不断变化，而试件并未与杆件分离，试件内部的应力在趋于近似均匀过程中，两端的应力大小也在随着时间推移发生变化，杆件内的残余波对试件的影响作用有差异，使得试件两端应力差相对值变化不一致。

试件的长径比越大试件内部的应力波反射次数减少，试件的平衡状态必然会引起加载应变率的变化，进而影响其他动态力学指标，如长径比为0.8的试件，其动态峰值强度呈现出高离散性，相对应的加载应变率离散性也大于其他组别试验结果。与无静载约束冲击试验不同，在同等冲击气压作用下，三维静载组合条件下的试件保持了很好的完整性。因此，在进行岩石动力学性质探究时，在除去试件自身结构性影响的前提下，需要选择合理的试件长径比，以期得到较为稳定可靠的试验数据。相比与无静载约束冲击花岗岩、大理岩等脆性材料试件长径比优先范围的0.7～0.8[15]，结合本文数据分析结果，静载组合条件下的冲击试验宜选用长径比为1.0的试件开展后续试验研究，冲击荷载作用过程中加载变率的同时，试件两端应力能保持较长时的平衡状态，以得到更为真实的材料的本构关系。值得一提的是，虽然无法实现上述讨论中完美的应力平衡，但相比实际工程中的炸药爆炸作用瞬间，已可以满足分析精度。由于文章所讨论的围压及轴压强度远小于致使试件强度离散的围压约束值[24]，因此，在低静载(≤10 MPa)约束条件下进行冲击试时，本文所得出优选的长径比结果依然适用；但当施加的静载约束强度较大时，该结果是否依然适用，需进一步探讨。