平面爆破P波扰动下深埋圆形衬砌隧道瞬态动力响应解析解研究*
2022-09-20高鑫鑫梅万全韩高升潘鹏志张义云
李 梅,高鑫鑫,梅万全,雷 涛,韩高升,潘鹏志,张义云
(1.武汉理工大学 a.资源与环境工程学院;b.土木工程与建筑学院,武汉 430070;2.中国科学院 武汉岩土力学研究所岩土力学与工程国家重点实验室,武汉 430071)
深埋长大隧道工程钻爆法施工过程中,产生的瞬态应力波会严重扰动既有隧道,对既有隧道造成的破坏不可忽视。因此,计算地下结构在动荷载下的动力响应解进而分析其变化特点具有重要意义。
目前,对爆破扰动下隧道结构动力响应计算多集中在稳态分析,其解析解多以波函数展开法为基础。Yi等通过对深埋圆形衬砌隧道在平面P波作用下衬砌隧道的动应力集中系数(DSCF)进行解析计算[1],研究了高频及低频入射波情况下动力影集中系数的变化规律,以及围岩不同位置上爆破波主频和围岩物理力学指标对动应力集中系数的影响[2,3];在此基础上,Fan等在接触面处引入线性弹簧模型[4],系统研究岩体和衬砌的无量纲波数、界面弹簧常数和衬砌厚度对动应力集中系数的影响;Lu等通过计算圆形隧道围岩质点速度响应的解析解[5],分析波源与隧道轴线的比例距离和隧道波长半径比对径向速度比例因子(RVSF)和环向速度比例因子(HVSF)的影响。
然而,实际工程施工扰动以瞬态波的形式传播,对稳态波的研究成果不能全面描述瞬态波扰动对结构的动态影响。因此,在稳态解的基础上,部分学者用数值逆变换或梯形求积等方法对瞬态弹性波入射时无限弹性介质中隧道的解析解及动力响应影响进行了研究[6-10]。梅万全等采用Den Iseger法数值逆变换,推导了深埋无衬砌隧道瞬态响应的理论公式[6],采用弹塑性细胞自动机中的动力模块模拟爆破引起的弹塑性动力响应,研究隧道不同位置的动应力集中系数及径向和环向速度比例系数变化。Li等首次推导出了定量评估爆破荷载作用下圆形隧道周围相对速度的理论公式[7],从理论上详细研究了波长与隧道直径比对振动速度放大效应的影响。Li等用梯形求积法[8-10],计算深埋无衬砌隧道的动应力、速度和位移等瞬态响应理论解,并采用二维PFC数值模型对理论分析进行了验证,研究静态地应力和动态卸荷波耦合作用下既有隧道的破坏特征,并进一步从瞬态波的卸荷速率、卸荷路径、地应力及开挖半径等角度分析隧道周围的动力响应。
由上可知,对爆破扰动下深埋隧道结构的动力响应瞬态解研究目前主要集中在无衬砌隧道,采用数值逆变换法和梯形求积法求解无衬砌隧道的动力响应,且对接触面处和隧道内的动力响应研究比较少。而实际工程中大多隧道有衬砌,故开展爆破扰动下有衬砌隧道结构瞬态动力响应研究很有必要。鉴于相同计算精度下,数值逆变换法求解及编程复杂,因此,论文以深埋圆形有衬砌隧道为研究对象,采用波函数展开法和梯形求积,计算平面爆破P波扰动下隧道瞬态动力响应解析解,分析爆破扰动对隧道接触面处和隧道内不同位置的动应力集中系数(DSCF)及径向(RVSF)和环向(HVSF)速度比例系数的影响。
1 爆破P波(瞬态)扰动下深埋圆形衬砌隧道动力响应解析解
研究爆破P波对有衬砌隧道瞬态动力响应,可在稳态解的基础上进行,即通过对P波动力扰动的稳态解进行梯形求积,求得瞬态解析解,进而分析围岩及隧道结构的动力响应特征。
图1所示为位于无限空间介质中的深埋圆形衬砌隧道模型,围岩和衬砌均为弹性、均质和各向同性材料,且隧道无限长,可将该模型视为平面应变模型。隧道衬砌内半径为a,外半径为b,爆破P波沿X轴正向传播。

图 1 爆破P波扰动下深埋圆形衬砌隧道模型Fig. 1 Model of deep circular lining tunnel under blasting P-wave disturbance
1.1 深埋圆形衬砌隧道波场分析
根据图1,平行入射稳态平面P波可表示为[11]
φ(i)=φ0ei(αsx-ωt)
(1)
利用波函数展开法,上式可写为
(2)
式中:φ0为入射P波波幅;αs=ω/Cps为围岩介质的纵波波数;ω为入射波频率;Cps为衬砌中的P波波速;i为虚数单位;r为隧道半径;Jn为第一类n阶Bessel函数,其中,当n=0时,εn=1,当n>0时,εn=2。
当入射P波传播围岩与衬砌之间的接触面时,接触面的存在使岩体中产生反射P波和反射SV波,可由第一类Hankel函数分别表示为
(3)
(4)
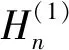
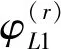
(5)
(6)
(7)
(8)
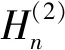
1.2 边界条件和稳态P波扰动下的动力响应解析解
假设围岩与衬砌之间理想接触,即位移和应力连续
当r=b时
(9)
当r=a时
(10)
式中:σrrs、σrθs分别表示围岩内的法向应力和切向应力;σrrL、σrθL分别表示衬砌内的法向应力和切向应力。
边界条件结合应力和位移势关系,即可得待定系数An、Bn、Cn、Mn、Dn、Nn。
围岩和隧道衬砌内P波在传播方向上的应力强度可分别定义为
(11)
(12)
以此做归一化因子,定义隧道边界处的动应力集中系数(DSCF)为[6]
(13)
(14)
式中:σθθs、σθθL分别表示围岩和衬砌内质点的环向应力,其中,下标S、L分别表示围岩和衬砌。
使用类似的方法,用质点速度峰值的大小v0s=αsωφ0·e-iωt,v0L=αLωφ0·e-iωt将径向速度和环向速度归一化,定义径向和环向速度比例因子(RVSF)和(HVSF)为
(15)
(16)
(17)
(18)
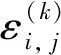
1.3 瞬态P波扰动下动力响应解析解
在上节所求的稳态P波扰动下隧道动力响应解析解的基础上,推导瞬态解析解,从而分析瞬态P波扰动下隧道的动力响应。
参考既有文献[12-14],用三角形爆破荷载函数定义爆破荷载的时间历程,即式(19)
(19)
图1模型中,入射波到达衬砌外边界时开始计时(即r=b时时间为零)。经过的时间t被归一化为通过外半径b所需的时间
τ=Cpst/b
(20)
通过傅里叶变换,任意输入函数f(t)引起的弹性系统瞬态响应可表示为
(21)
式中:χ(xi,ω)为系统的导纳函数,为单位振幅下系统的稳态响应,可用公式(13)~(18)表示;F(ω)为爆破荷载函数(扰动函数)f(t)的傅里叶变换。
沿隧道边界输入的爆破荷载函数f(t)的傅里叶变换F(ω)用Heaviside阶跃函数的傅里叶变换表示
(22)
式中:Re(ζ)=αsb。
系统的导纳函数可以简化为
χ(xi,ω)=R(ω)+iI(ω)
(23)
式中:R(ω)和I(ω)表示频率响应的实部和虚部。
对于因果函数,可用正弦函数表示瞬态响应,通过Heaviside阶跃函数输入引起的脉冲响应,可以用下式积分表示
(24)
根据Duhamel积分,任意扰动函数f(t)的动态响应表示如下

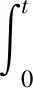
(25)
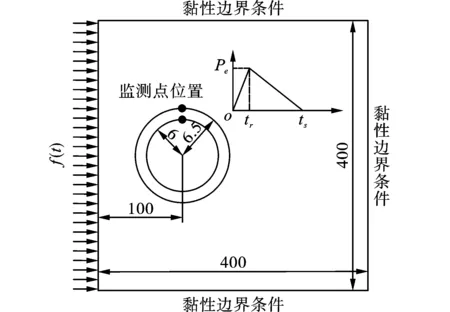
当0≤t (26a) 当tr≤t (26b) 当t≥ts (26c) 式中,R(ω)由公式(13)~(18)的实部表示[7,8],根据公式(26)及梯形求积法即可确定爆破荷载作用下隧道的瞬态响应解析解。 为了验证梯形求积法求得的解析结果的正确性,运用FLAC3D软件和工程岩体破裂过程分析软件(CASRock)中的动力分析模块CASRock.Dyna计算的数值结果与Matlab计算的解析解进行对比验证[15-19]。 选取文献[6]中的算例,隧道横断面为圆形,内径a=6.0 m,外径b=6.5 m,监测点位于隧道拱顶,数值模型尺寸为400 m×400 m×2 m,如图2所示。在计算模型的左侧边界施加爆破应力波,模拟隧道受到的瞬时动力扰动,时间从爆破荷载传至隧道接触面处开始计算,爆破荷载上升时间2.5 ms,爆破荷载施加总时间12.5 ms。其他边界设置为粘性人工边界,吸收边缘反射的应力波。其他参数为:围岩的弹性模量Es=50.00 GPa、密度2700 kg/m3、泊松比0.20,衬砌的弹性模量EL=30.00 GPa、密度2500 kg/m3、泊松比0.25。 计算得到的有衬砌隧道DSCF如图3所示。位于围岩与衬砌接触面处监测点的DSCF明显大于衬砌内部监测点,理论计算DSCF峰值略大于数值模拟DSCF峰值,且数值结果与理论结果的差异相比曲线振幅较小,其差异可忽略,说明用梯形求积计算爆破扰动下有衬砌隧道的动力响应合理。 图 2 数值模型(单位:m)Fig. 2 Numerical model(unit:m) 图 3 动应力集中系数的梯形求积解与FLAC3D数值模拟解比较Fig. 3 Comparison between trapezoidal quadrature solution of DSCF and FLAC3D numerical simulation solution 锦屏二级水电站1#,3#引水隧洞工程,引水隧洞采用TBM和钻爆法结合开挖,洞线平均长度16.67 km,全洞一般埋深1500~2000 m,最大埋深2525 m,其中,TBM开挖段为圆形隧洞,开挖半径约6.6 m,衬砌厚度0.6 m,属于典型的深埋长大隧洞。 引水隧洞主要穿越三叠系下统、杂谷脑组、上统、白山组、盐塘组共5套地层,在TBM开挖段埋深较大、地应力较高的白山组地层中选取垂直于引水隧洞轴线的竖直剖面作为计算断面,计算模型材料物理学参数如表1所列。 表 1 材料物理学参数 采用上述解析解公式研究爆破扰动下隧洞瞬态动力响应分布规律,取爆破荷载标准化上升时间τr=5,总时间与上升时间的比值ts/tr=5,其他计算参数如表1所列。爆破扰动对隧洞接触面处和隧洞衬砌内的动应力集中系数及速度振动比例因子的计算结果如图4所示。隧洞衬砌内与隧洞接触面处的动力响应曲线形状相同,幅度显著减小。 爆破荷载加卸载过程中产生的动应力集中系数见图4(a)和图4(b),爆破扰动过程中,隧洞和衬砌接触面处及隧洞内表面处均产生了明显的动应力集中,主要表现为拉应力集中于θ=0和π处,压应力集中于θ=π/2处。θ=0和π处的DSCF时程曲线趋势大致相同,加载过程中,DSCF迅速增加到第一个正峰值,然后下降到最小值;卸载过程中,DSCF从最小值增大到次正峰值,然后减小到零。θ=π/2处的DSCF时程曲线趋势大致相同,加卸载过程中,DSCF增加到第一个正峰值后再降到最小值,最后减小到零。 图 4 平面爆破P波扰动下隧道动力响应解析结果Fig. 4 Analytical results of tunnel dynamic response under plane blasting P-wave disturbance 爆破荷载在达到θ=0(图4(c))处,介质径向速度迅速达到峰值并逐渐减小到零,在θ=π/2(图4(d))时,介质径向速度产生轻微震荡,但速度振动幅值较小。 考虑到密度和泊松比对衬砌动应力集中系数影响较小[20],因此,主要研究爆破P波扰动下围岩与衬砌弹性模量比对隧洞瞬态动力响应峰值的影响,分析结果可参与指导隧洞减震施工。引入围岩与衬砌介质弹性模量比γ=Es/EL,计算参数见表1。图5~7给出了弹性模量比γ=1~10时,洞室动应力集中系数峰值、径向和环向速度比例因子峰值分布。 当γ<2时,随着γ的增加,洞室衬砌内动应力集中系数峰值、径向和环向速度比例因子峰值降低最快;γ=4时,动应力集中系数峰值下降值占对应最大下降值的80%,径向和环向速度比例因子峰值下降值占对应最大下降值72%。但在γ从1到10增大过程中,围岩与衬砌的接触面处的动应力集中系数峰值、径向和环向速度比例因子峰值无显著变化,可见,对围岩进行加固,提高其弹性模量,可使部分衬砌中的能量转到围岩,且围岩与衬砌弹性模量比越大,越有利于隧洞结构稳定。 图 5 动应力集中系数峰值随γ的变化Fig. 5 Variation of maximum DSCF with γ 图 6 径向速度比例因子峰值随γ的变化Fig. 6 Variation of maximum RVSF with γ 图 7 环向速度比例因子峰值随γ的变化Fig. 7 Variation of maximum HVSF with γ 论文基于波函数展开法,在稳态解的基础上,采用梯形求积,推导了平面爆破P波扰动下圆形有衬砌隧道动力响应的瞬态解析解,分析了爆破P波扰动对隧道衬砌接触面处和隧道内的动应力集中系数(DSCF)及径向和环向速度振动(RVSF、HVSF)的影响。研究成果可为类似工程计算提供参考。主要结论如下: (1)隧道衬砌与围岩之间接触面处拱顶及两侧拱腰位置的DSCF、RVSF和HVSF的变化趋势相同,且接触面处的响应峰值要大于衬砌内侧。 (2)隧道顶板处的DSCF和HVSF效应远比左右侧壁处显著,相反,隧道两侧壁处的RVSF效应远比顶板处显著,且动应力集中系数响应峰值远大于速度振动响应峰值。 (3)增大围岩与衬砌弹性模量之比可有效降低衬砌内动应力集中系数峰值和速度比例因子峰值,但超过2~4倍比例后,降低效果有限,建议对围岩采取注浆加固等措施提高围岩与衬砌弹性模量比,保证隧道结构稳定。2 梯形求积法解析解结果有效性验证

3 爆破P波扰动下圆形衬砌隧道动力响应分析
3.1 工程背景

3.2 隧洞瞬态动力响应分布规律


3.3 围岩与衬砌弹性模量比对隧洞瞬态动力响应峰值的影响

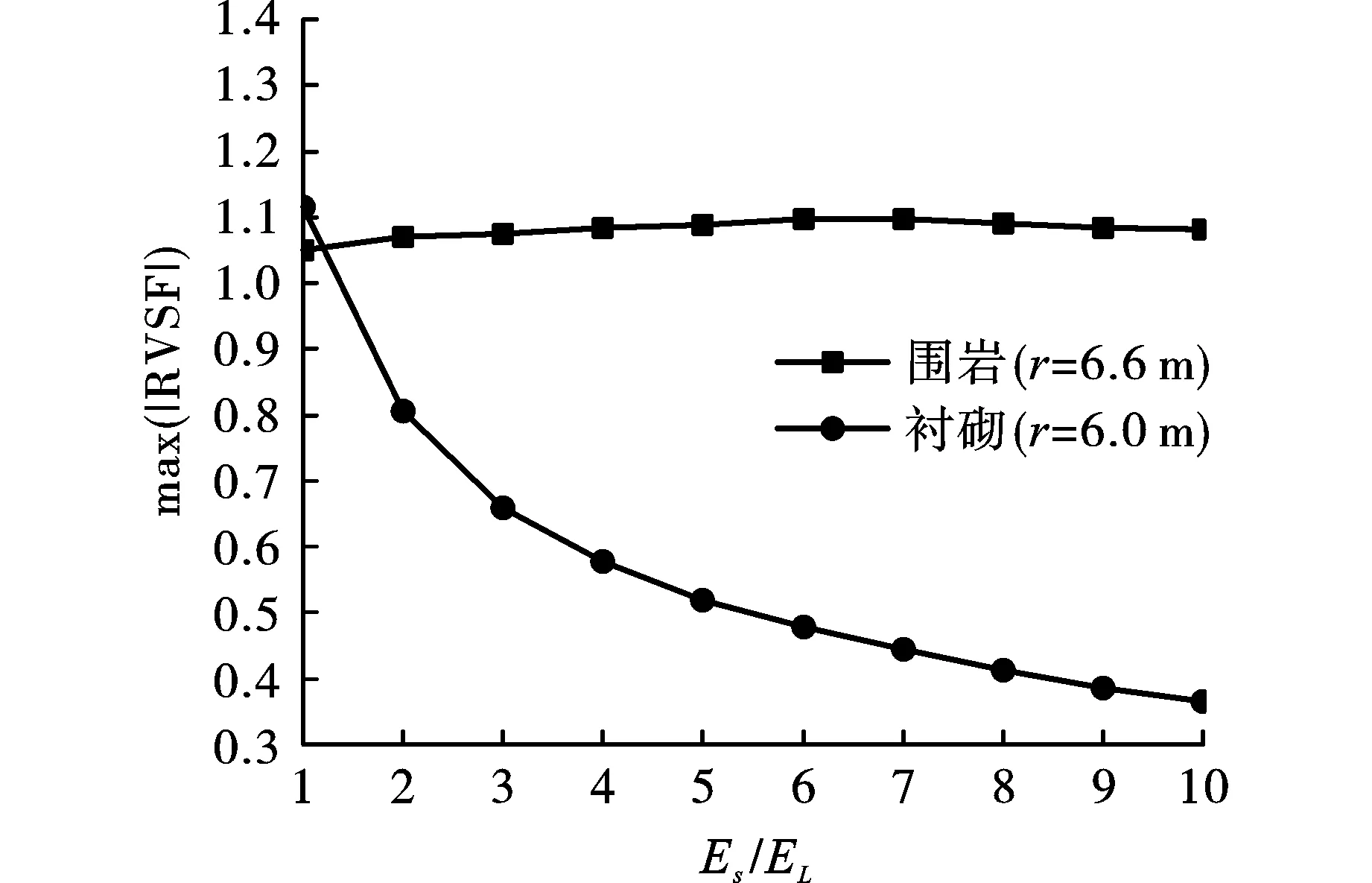
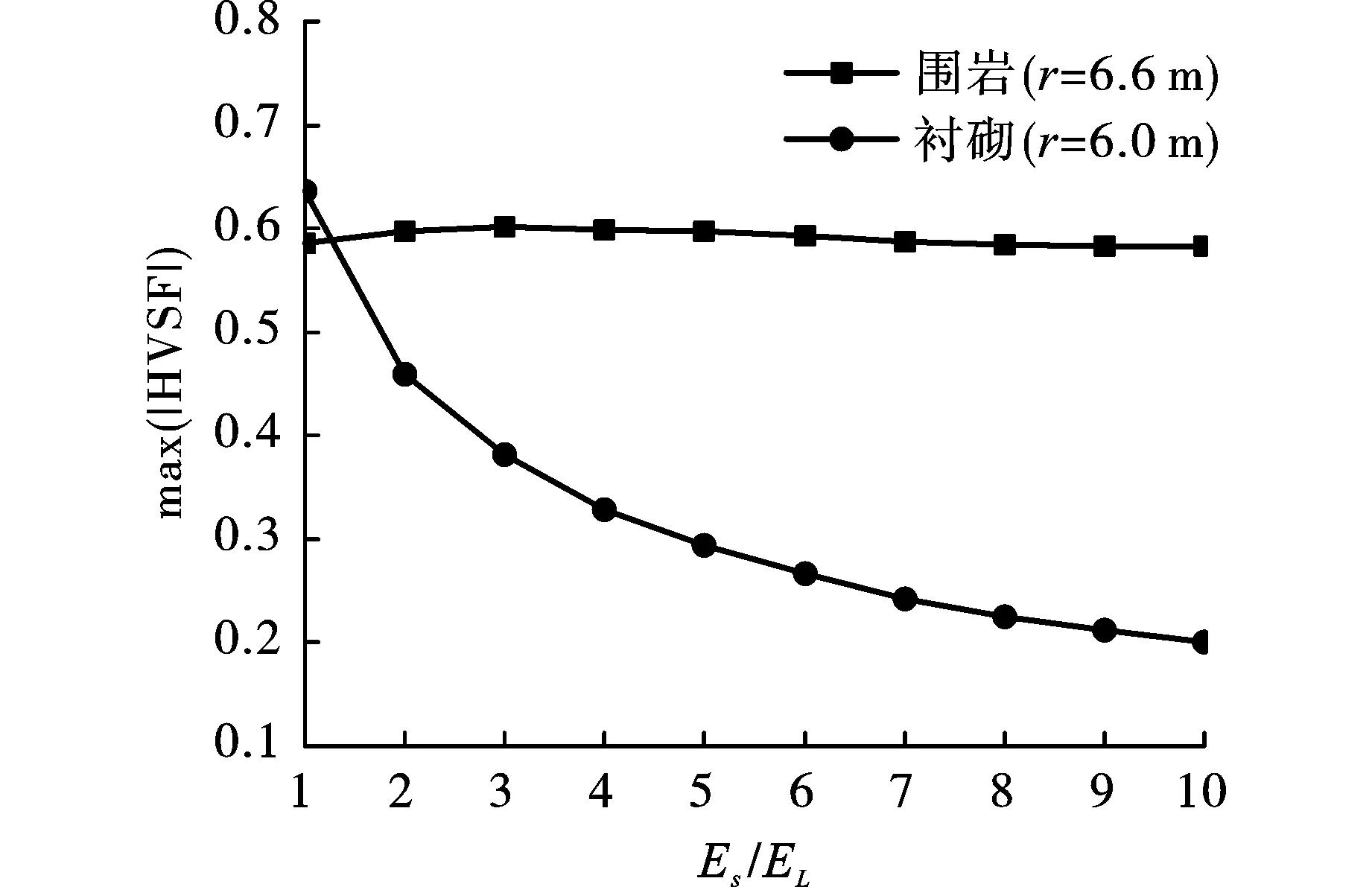
4 结论
