中主应力对冻结黏土力学特性影响的试验与分析
2022-10-13祝林立马芹永
祝林立马芹永
(安徽理工大学 土木建筑学院,安徽 淮南 232001)
0 引言
随着浅部资源的枯竭以及人类对资源需求增加,对于深部资源的开采在全球掀起了新的浪潮[1-4]。在深部资源开采的过程中,不可避免地会遇到水系丰富的地层、软弱岩层等特殊地层,给施工带来了诸多不便[5-8]。人工冻结法灵活多变,适应性强,且冻结壁强度高,连续性好,广泛运用于煤矿立井等特殊工程,使得深部冻土的力学特性受到了广泛的关注[9-13]。在实际工程中,人工冻结法形成的冻土往往处于三向不等的复杂应力状态[14]。因此,了解和掌握冻土在真三轴应力状态的强度和变形特性,有助于进一步优化施工参数,节约成本。
国内外众多学者通过开展真三轴试验和数值模拟系统地研究了中主应力对岩土材料力学特性的影响。Mogi K[15]率先研究了中主应力对岩石强度和破坏模式的影响,其试验结果表明岩石的强度与小主应力和中主应力息息相关,且中主应力会显著提升岩石的力学特性;Haimson B C等[16]研究发现,随着花岗岩的强度随着中主应力的增加,呈现出先增加后降低的变化趋势,且花岗岩在真三轴应力状态的强度均大于其在轴对称应力状态下的强度;Zhang Y 等[17]研究了小主应力和中主应力对北山花岗岩能耗特性的影响,总应变能和弹性应变能随中主应力和小主应力的增大而增大,且小主应力对岩石破坏模式和能量演化特征的影响程度大于中主应力;尹光志等[18]对砂岩开展了真三轴压缩试验发现,随着中主应力的增加,砂岩的强度和扩容起点逐渐降低;Cai M[19]采用连续-离散元耦合分析模型,认为隧道表面的平行裂隙和微裂纹的形成是由于材料的非均质性以及较高的中主应力引起的;Manouchehrian A等[20]借助ABAQUS模拟了岩石在多轴卸荷条件下的破坏特征;Duan K 等[21]通过离散元模拟研究发现,中主应力对砂岩的破坏应力、弹性模量、破坏面倾角以及破坏模式具有显著的影响。以上研究均表明,中主应力对岩土材料的宏观力学响应具有重要的作用,破坏应力随着中主应力的增加呈现出先增加后下降的变化趋势,具有显著的区间性。
现阶段主要借助常规三轴试验系统来研究土质、温度、含水(冰)量、应变率等因素对冻土在复杂应力状态下力学特性的影响,并取得了一系列显著的成果[22]。但是,大多局限在单轴或者轴对称应力状态,很少考虑中主应力的影响,不能还原冻土真实的力学效应[23-24]。陈敦等[25]借助冻土空心圆柱仪,率先开展了冻结黏土在真三轴应力状态下的试验,研究了平均主应力对冻土强度和变形特性的影响,并根据试验结果进一步分析了破坏准则的适应性[26];雷乐乐等[27]研究结果表明,大主应力轴方向角、中主应力比以及平均主应力对冻结黏土强度会产生显著的影响;Huang K等[28]借助冻土真三轴试验系统对冻结砂土开展了一系列真三轴试验,其试验结果表明,随着中主应力系数的增加,冻结砂土的强度表现出先增加后下降的变化趋势,当中主应力系数为0.6时强度最大。以上结果证明了冻土在真三轴应力状态下的力学特性更加复杂,因此,有必要进一步研究中主应力对冻土力学特性的影响。
1 真三轴试验
1.1 试样制备
试验用土取自淮南某基坑,其天然含水率为16%,塑限和液限分别为20.69%和43.44%。将原状土破碎、烘干、过2 mm 筛,颗粒级配曲线如图1所示。依据原状含水率,称取适量的干土和蒸馏水将其拌和均匀,接着放入保湿皿内浸润24 h;将上述湿土放入内部尺寸为100 mm×100 mm×100 mm 模具中分层击实;脱模后的试样包裹一层保鲜膜,将其放入-20 ℃的低温箱中冻结24 h,接着将试样在-10℃的低温箱继续冻结48 h。

图1 黏土颗粒级配曲线
1.2 试验仪器
冻土真三轴仪主要由温度控制系统、液压伺服加载系统、数字控制系统组成。该试验机一端为固定端,其余5个方向均可以独立控制,能够实现冻土在复杂应力路径下力学性能试验,如图2所示。

图2 冻土真三轴仪
1.3 试验方法
首先,将大主应力、中主应力和小主应力以20 N/s的速度同步加载至设定的小主应力,并固结30 min;接着维持小主应力恒定,将大主应力和中主应力同步加载至中主应力;然后,保持中主应力和小主应力恒定,大主应力以0.5 mm/min的加载速率进行加载,直至试样达到破坏状态。
本试验主要目的是研究中主应力对冻结黏土强度和变形特性的影响,具体试验方案如表1所示。

表1 不同中主应力条件下真三轴试验方案
2 试验结果
2.1 偏应力-主应变曲线
图3为不同中主应力条件下的应力应变曲线。从图3可以看出,在不同试验条件下,冻结黏土的偏应力-大主应变曲线均呈现出应变硬化的特性,其中偏应力为大主应力与小主应力之差;当试样处于轴对称应力状态时,中主应变和小主应变的曲线几乎全部重合;与常规三轴试验结果不同,在真三轴应力状态下,中主应力和小主应力方向上的应力应变曲线不完全重合;随着中主应力的增加,两者之间的差距更加显著,这表明中主应力会对试样的变形产生显著的影响。Kong R等[29]也发现类似的规律,其认为这是由于各向异性膨胀造成的。可以看出,当试样处于真三轴应力状态时,破坏强度和曲线的斜率均大于常规三轴应力状态,这表明中主应力会提升冻土抵抗破坏和变形的能力,依据常规三轴的试验结果低估了冻土材料的力学特性。
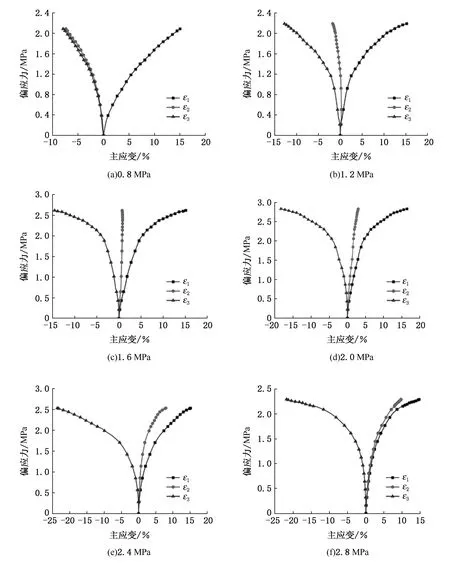
图3 不同中主应力下真三轴试验应力应变曲线
2.2 大主应变-中主应变关系
图4反映了大主应变和中主应变之间的关系。当σ2<1.6 MPa时,中主应力方向表现为膨胀变形;而当σ2≥1.6 MPa时,该方向的变形表现为压缩变形。从试验结果来看,可能存在一个临界值σ2ps,当σ2=σ2ps时,中主应变接近于0,试样近似处于平面应变状态;当σ2<σ2ps时,中主应力方向发生膨胀变形;当σ2>σ2ps时,中主应力方向产生压缩变形。

图4 大主应变-中主应变曲线
2.3 大主应变-小主应变关系
图5反映了中主应力对大主应变-小主应变关系曲线的影响。由图5可知,小主应变均为负值,表明试样在小主应力方向均发生膨胀变形;大主应变和小主应变曲线大致呈线性分布,曲线斜率随中主应力的增加而增加。这意味着,在相同的大主应变下,中主应力越大,小主应变的绝对值越大,即试样在小主应力方向越容易产生膨胀变形。由于采用应力控制,大主应力和中主应力随着加载时间的增加而增大,对这两个方向上的挤压作用越强;而小主应力维持恒定,不能有效约束该方向的位移,从而产生较大的膨胀变形。
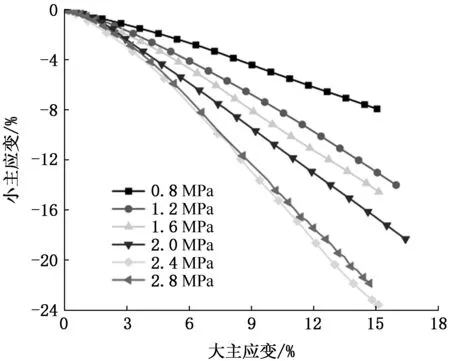
图5 大主应变-小主应变曲线
图4和图5综合反映了中主应变与小主应变和大主应变之间的关系,当中主应力小于1.6 MPa时,中主应变为负值,当中主应力大于1.6 MPa时,中主应变为正值,小主应变始终小于零。最小耗能原理能够合理解释上述试验现象,物体的变形总是朝着消耗能量最小的方向进行,也就是朝着变形最容易的方向进行。中主应力的增加意味着对该方向的约束作用逐渐增强,故中主应力方向上的变形由膨胀变形向压缩变形转变。相比之下,小主应力方向的约束较小,更容易产生膨胀变形。
3 结果分析
3.1 大主应力和变形模量的变化趋势
从图6可以看出大主应力和变形模量随中主应力的变化规律。变形模量以割线模量来表示,割线模量为应力达到破坏应力的50%处的应力应变比值。当中主应力从0.8 MPa 增长到2.0 MPa时,冻结黏土的强度和变形模量随着中主应力的增加而增加;当中主应力介于2.0~2.8 MPa时,其强度和变形模量表现出下降的趋势。值得注意的是,当试样处于真三轴应力状态时的强度和变形模量,均大于轴对称应力状态下的值,这进一步表明中主应力可提升冻结黏土的抵抗破坏和变形的能力。
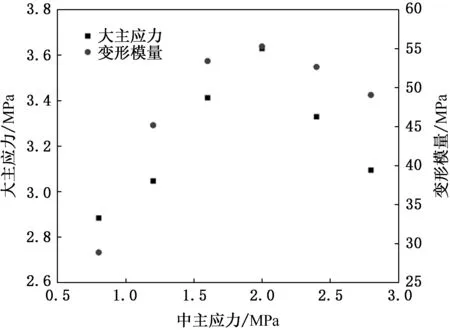
图6 大主应力和变形模量的变化趋势
3.2 偏应力理论值与试验值的对比
由图7偏应力理论值与试验值的对比可知,不同试验条件下的偏应力-大主应变曲线均表现出应变硬化的特性,大致符合双曲线关系。邓肯-张模型以广义胡克定律为基础,因其形式简单、参数少和易于确定而得到广泛应用[30]。因此,本文采用该模型来预测冻结黏土在真三轴应力状态下的应力应变关系。模型的数学表达式如式(1)所示。
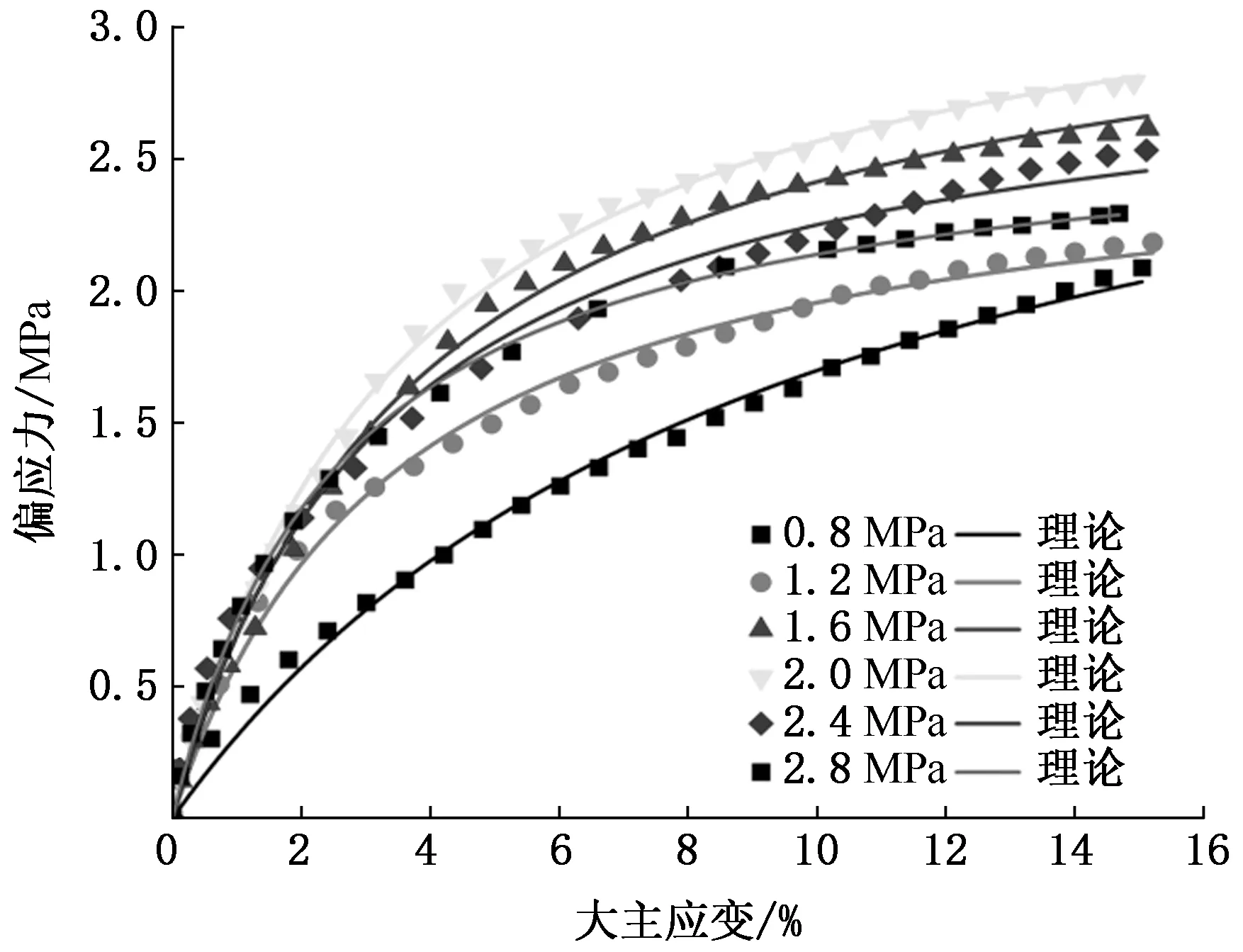
图7 偏应力理论值与试验值的对比

式中:m、n为拟合参数;ε1为大主应变,%;σ1为大主应力,MPa;σ3为小主应力,MPa。
拟合参数如表2所示。从图7可以看出,在不同中主应力条件下,邓肯-张模型可较为准确地反应出冻结黏土在复杂应力状态下的强度和变形特性。

表2 不同试验条件下的理论参数
4 结论
(1)冻结黏土的强度和变形模量表现出明显的相关性,当中主应力从0.8 MPa增长到2.0 MPa时,冻结黏土的强度和变形模量随着中主应力的增加而增加;当中主应力介于2.0~2.8 MPa时,其强度和变形模量表现出下降的趋势。
(2)存在一个临界中主应力(σ2ps),当中主应力接近该临界值时,中主应变接近于0,试样处于平面应变状态;当σ2<σ2ps时,中主应力方向发生膨胀变形;当σ2>σ2ps时,中主应力方向产生压缩变形。小主应力方向始终表现为膨胀变形,且变形幅度随中主应力的增加而增加。
(3)在不同中主应力条件下,冻结黏土的应力应变曲线均表现出应变硬化的特性,邓肯-张模型能够准确地预测出冻结黏土在复杂应力状态下的强度和变形特性。
