基于MEEMD与相关分析的行星齿轮箱测点优化*
2022-02-22魏秀业程海吉史大正范星宇
魏秀业 程海吉 贺 妍 史大正 范星宇
(①中北大学机械工程学院,山西 太原 030051; ②先进制造技术山西省重点实验室,山西 太原 030051;③国能榆次热电有限公司,山西 晋中 030600; ④黄河万家寨水利枢纽有限公司,山西 太原 030009)
机械传动设备的故障问题一直困扰着机械工程的技术人员。在故障诊断过程中,传感器的数量会极大地增加故障诊断的成本。王子涵等人对局部线性嵌入的行星变速箱测点进行优化[1],张林等人提出基于模糊聚类与灰色理论的机床主轴温度测点优化方法[2]。本文以行星齿轮箱为研究对象,提出了一种基于改进的集成经验模态分解(MEEMD)[3]信息熵与相关分析的行星齿轮箱测点优化方法。
1 MEEMD分解算法
经验模态分解(EMD)与小波包分解信号等时频分析方法相比,更能反映信号的物理意义,但无法克服模态混叠现象。EEMD算法即使是对EMD分解得到的IMF分量求均值,以消除随机白噪声的影响,但还是会发现噪声消除不完全,使得部分IMF有失真且信号重构误差大。因此,本文采用了改进的集成经验模态分解(MEEMD)方法,有效地消除模态混叠现象,减少了重构误差。具体分解步骤如下:
(1)将原始信号x(t),添加2组振幅和标准差相等且方向相反的正负白噪声mi(t),得到:
(1)
式中:ai为幅值;Me为白噪声的对数。
(2)

(3)分解信号得到每阶IMF分量:
(3)
(4)因为yj(t)存在模态分裂的问题,在此需对yj(t)进行EMD分解,有
(4)

2 信息熵
信息熵是一种反映信息不确定性的指标,计算过程简单高效。信息的不确定性程度越高,信息熵的值就越大,反之越小。高信息度的信息熵是非常低的,低信息度的信息熵则相当高。信息熵具有单调性,非负性和累加性的性质。本文利用信息熵的特性,使用信息熵作为振动测试信号的特征值。信息熵表示为:
(5)
3 测点的相关性分析[4-6]
相关系数r是研究变量之间线性相关程度的物理量,是反映2个变量之间相关程度的指标,它最早由著名统计学家卡尔·皮尔逊设计。相关系数较为常用的是皮尔逊相关系数。绝对值数值大小在0~1变化。其表达式为:
(6)
若直接对行星齿轮箱振动的原始信号提取特征值进行相关性分析,由于存在强烈的噪声信号干扰,导致分析出各测点之间的相关性不够准确。因此,本文提出了一种基于改进的集成经验模态分解(MEEMD)信息熵与相关分析的行星齿轮箱测点优化方法。基本步骤如下:
(1)信号数据采集:布置试验台,人为设置包含单一工况与复合工况的5种工况,采集各工况的振动加速度信号。分别依次对各工况各测点数据进行采集,组成各信号样本。
(2)特征提取:分别对不同测点的各类工况样本依次截取时间为0.2 s数据进行MEEMD分解,分解出多个IMF分量。计算各分量与原始数据的相关性。筛选相关性大的P个分量作为有效分量,并进行信息熵计算,将其作为特征向量。构造成特征向量矩阵。
(3)控制同一工况不变,分别对不同测点的特征向量矩阵X和Y进行相关分析。依次将5种工况各测点的相关性进行求解。列表对比筛选出每种工况相关性最低与相关性最高的一组测点。
(4)利用信息熵的累加性原则,控制同一测点不变,对复合工况和复合工况中包含工况的熵值和组成的特征向量矩阵X和Y进行相关性分析。依次对各测点的数据进行求解。列表对比筛选出相关性较低的测点。对各测点的相关性大小进行排序。
(5)优化结论:对于控制同一工况不同测点筛选出的相关性最高的5组测点,对比分析出相对冗杂多余测点。对于相关性最低的5组测点,分析对比出与最优测点相关性较低的测点定义为相对无效测点。控制测点不变,分析复合工况和复合工况包含工况的熵值和进行相关性计算,算出的各测点的相关性大小进行排序。两类分析方法进行综合分析,从而达到测点优化的目的。
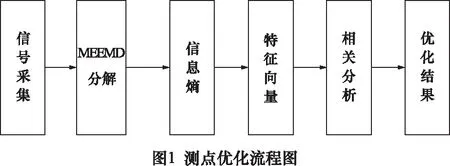
4 行星齿轮箱测点优化试验分析[7]
4.1 测点布置
本次试验使用如图2所示的试验台进行。
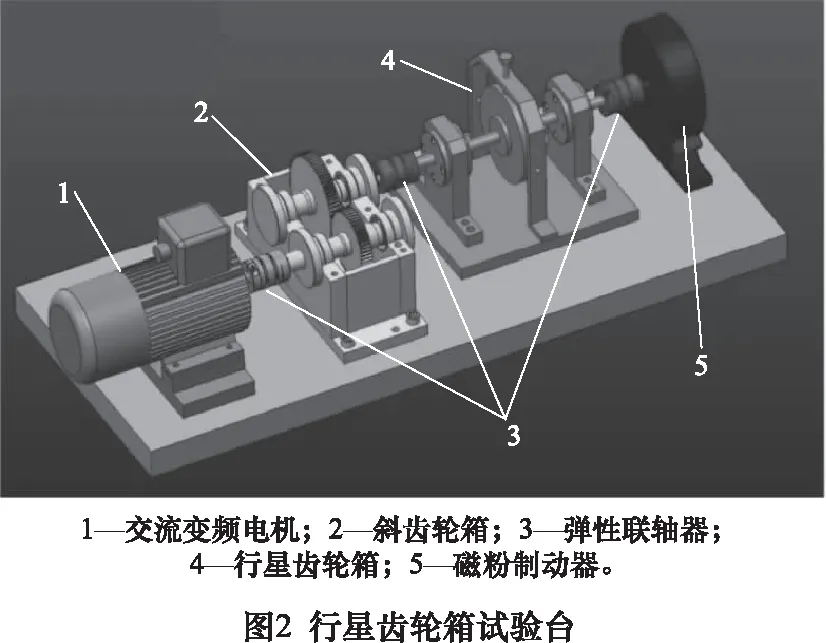

试验采样时将电机的转速调整到1 500 r/min,采样频率设置为10.24 kHz。设置负载为0.3 Α。检查测点信号是否正常。
本次试验设置5种工况11个测点进行振动信号采集,其中通过人为设置4种故障工况模拟行星齿轮箱微弱故障,5种工况分别为:正常工况、行星轮单齿裂纹、太阳轮轴承外圈裂纹、复合工况一(太阳轮齿面磨损+行星轮2个齿磨损)、复合工况二(太阳轮齿面磨损+行星轮2个齿磨损+行星轮单齿裂纹),依次定义为工况一~工况五。依次更换齿轮,对5种故障工况的振动信号,依次进行采集。各测点名称如表1所示。
4.2 选取故障特征值
运用MEEMD信息熵对行星齿轮箱振动信号进行特征提取。对由上节采集到的5种工况下的行星齿轮振动信号分别进行MEEMD分解,截取时间为0.2 s,采样点数为2 048,分解得到多个IMF分量,其中以正常工况1测点数据MEEMD分解图为例如图4与图5所示。

表1 行星齿轮箱测点名称表

分解得到的IMF分量,采用相关系数进行筛选包含主要故障的分量。原始信号与非真实分量的相关系数较小。以各工况下测点1~测点3原始信号与各IMF分量的相关系数为例如表2所示,通过分析研究各分量与原始信号数据相关系数的大小,发现各工况下原始信号与IMF5以前分量的相关系数均大于0.1,由此认为前5个IMF分量为真实分量。
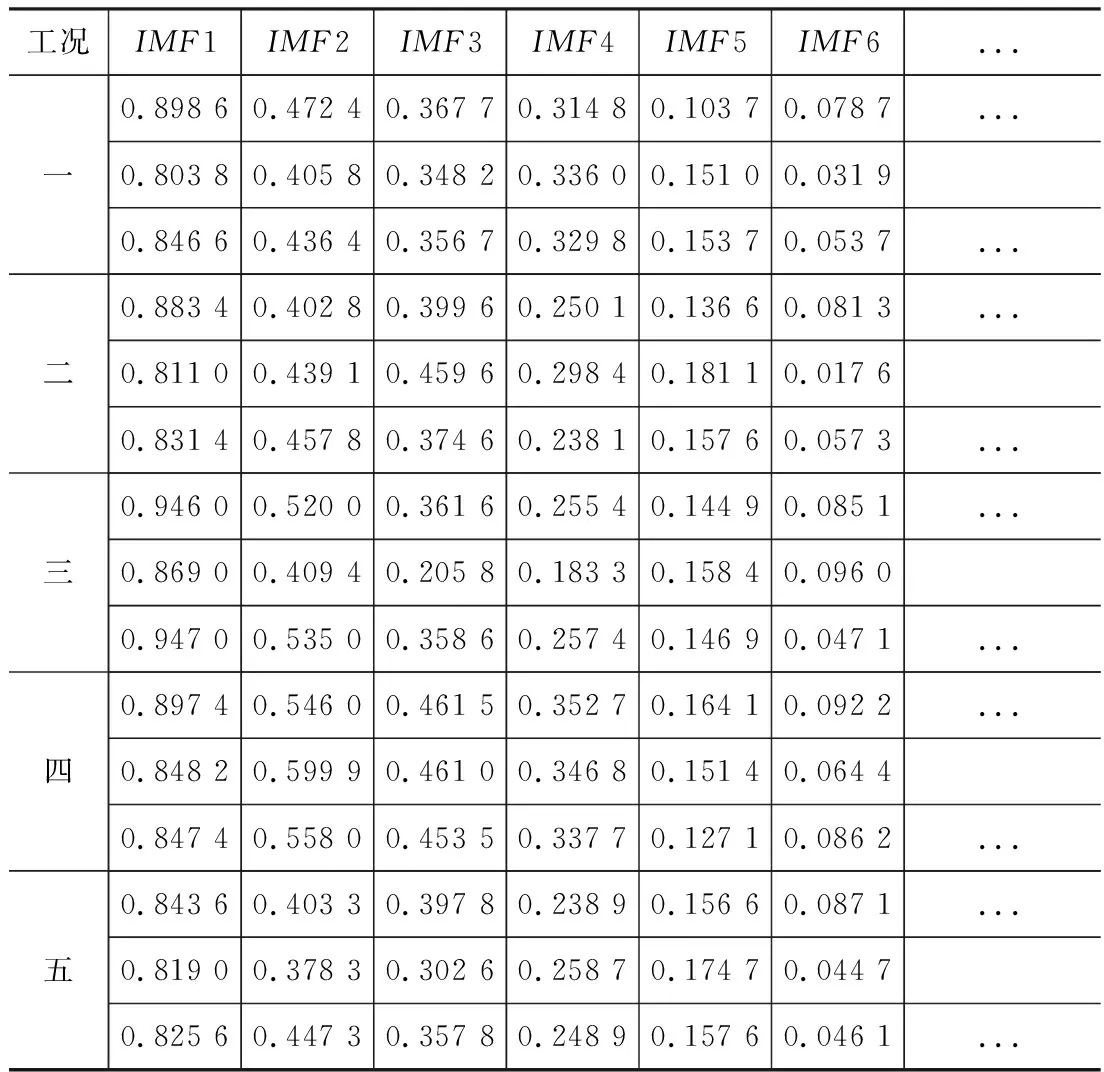
表2 各工况测点1~3相关系数表
对各工况各测点信号MEEMD分解得到的前5个IMF分量进行信息熵的计算,构成特征向量,组成样本特征矩阵。以工况二(行星轮单齿裂纹)的特征向量矩阵为例如表3所示。

表3 工况二各测点的特征向量
4.3 相关性分析
控制同一工况,对不同测点的特征向量矩阵进行相关性分析。依次对5种不同工况的数据进行计算,筛选出相关性最高和相关性最低的测点组数。以工况三(太阳轮轴承外圈裂纹)不同测点的相关性为例如表4所示。
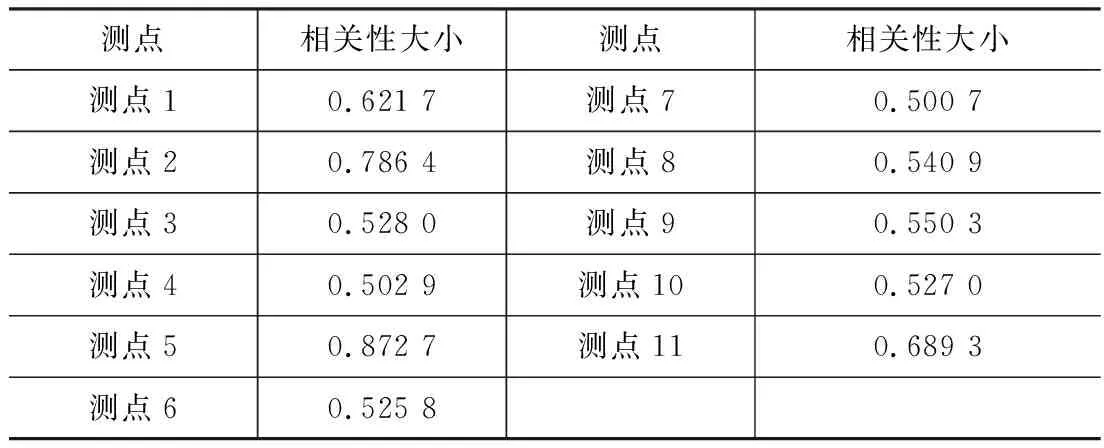
表4 太阳轮轴承外圈裂纹各测点的相关性
控制同一测点,对复合工况和复合工况所包含的工况的熵值和进行相关性分析。本文复合工况二为:太阳轮齿面磨损+行星轮两个齿磨损+行星轮单齿裂纹。复合工况一为:太阳轮齿面磨损+行星轮两个齿磨损。工况二为:行星轮单齿裂纹。依次对各测点复合工况二与复合工况一加工况二的熵值数据进行相关性计算。计算结果如表5所示。
4.4 结果与分析
通过数据结果表明。在控制同一工况,不同测点的相关性分析时。统计数据如图6所示。研究结果显示工况一、工况三、工况四均为测点6与测点8的相关性最高。工况二、工况五均为测点5与测点7的相关性最高。所以测点6与测点8优选其一,测点5与测点7优选其一。
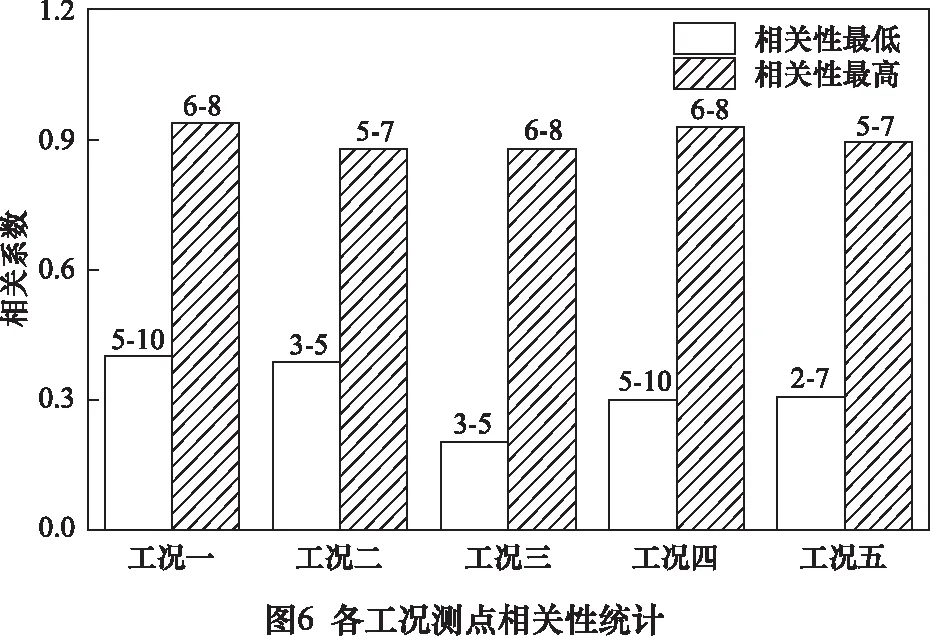
研究数据结果显示工况一、工况四均为测点5与测点10的相关性最低。工况二、工况三均为测点3与测点5的相关性最低。工况五为测点2与测点7相关性最低。若测点5为较优测点,则测点3与测点10为相对较差测点,不然则相反。测点2与测点7亦然。
在控制同一测点,不同工况的相关性分析时。对复合工况和所包含的工况的熵值和进行相关性分析结果统计如图7所示。
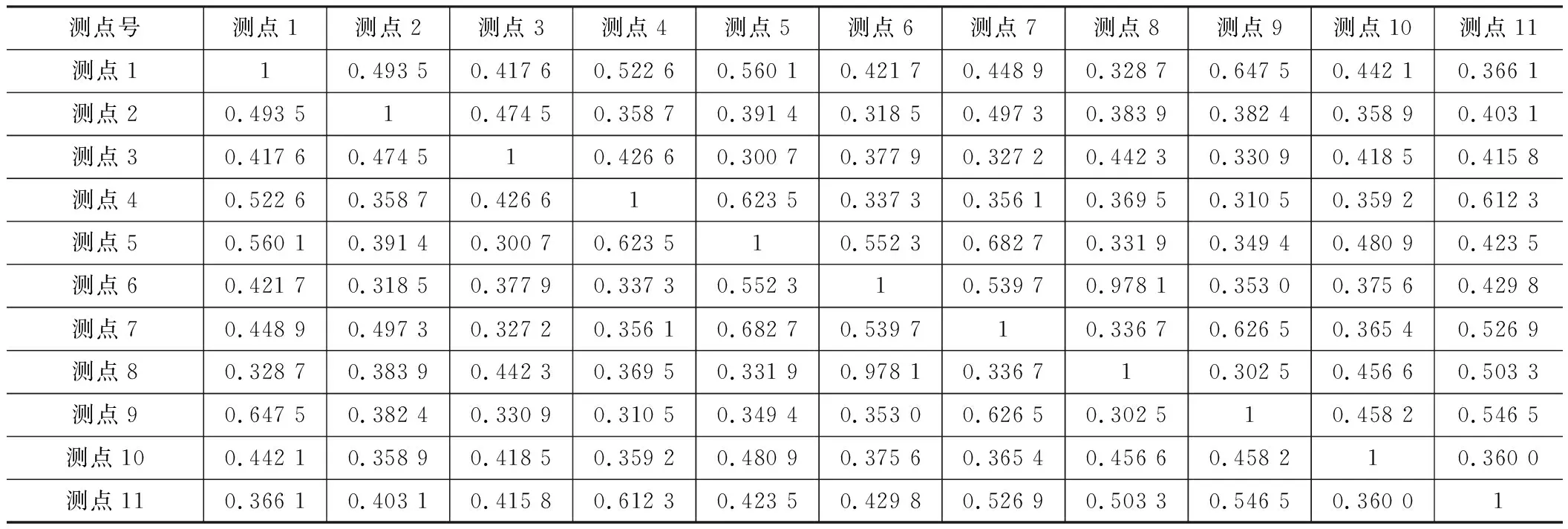
表5 各测点相关性数据统计

分析数据结果显示测点5的相关性最大为0.872 7。测点4与测点7的最小,分别为0.502 9和0.500 7。根据统计图结果可分析。测点6与测点8优选测点8,测点5与测点7优选测点5。测点3与测点10为相对较差测点。
综上所述,用两种相关分析法综合表明,优化剔除的测点为:测点3、测点4、测点6、测点7、测点10。最终保留的优选测点为:测点1、测点2、测点5、测点8、测点9、测点11。
5 结语
分析结果表明,该方法能够有效优选出最优测点,减少在机械传动设备行星齿轮箱的故障诊断中传感器的数量,从而有效地降低了检测成本。
针对行星齿轮箱振动信号故障诊断中传感器布置数量的问题,本文提出的一种基于改进的集成经验模态分解(MEEMD)信息熵与相关分析相结合的行星齿轮箱测点优化方法。对于机械传动部件行星齿轮箱极易发生故障的问题,本文提到的方法对行星齿轮箱的故障检测中测点的布置,提供了很好的思路。针对传感器的冗杂问题有了很好的解决,极大地降低了经济成本。使得使用少量的传感器,检测出真实的故障信息。
本文具体创新点如下:
(1)本文采用MEEMD分解方法,将原始信号自适应地分解出11个IMF分量,将噪声干扰信号有效的区分,抑制了模态混叠现象。
(2)使用了信息熵叠加性的特性,用信息熵来表达样本数据的特征值,能够很好的表达故障特征。
(3)结合相关分析方法,采用控制变量的方法,从数据定量角度进行分析问题。
