水下爆炸气泡运动对自由液面形态影响研究*

2022-09-20周文哲徐立君郭锦泽刘筹资程永舟郑长青

爆破 2022年3期

周文哲，徐立君，郭锦泽，刘筹资，程永舟,3，郑长青

(1.长沙理工大学水利与环境工程学院，长沙 410114；2.湖南水利水电职业技术学院，长沙 410100；3.水沙科学与水灾害防治湖南省重点实验室，长沙 410114；4.珠海爆破新技术开发公司，珠海 519099)

水下爆破在现阶段是一种快速有效的水下施工技术，在水下作业的很多方面都有着不可替代的作用，有着广泛的应用[1]。水下爆炸形成的气泡脉动与自由液面相互作用产生形态不同的水冢[2]，水冢在重力的作用下回落到水面会对周围的结构等物体产生较大的冲击。当炸药的装药量过大，形成的水下波动会对周围的水生动植物产生冲击[3]，还会产生较大的水面波动，威胁周围船舶、建筑安全。因此研究水下爆炸气泡运动对水面形态的影响和水面兴波规律，对指导水下爆炸实施时周围建筑物的安全防护具有重要意义。

在水下爆炸气泡运动对自由液面影响方面，Szymezak等基于BEM方法[4]，对水下爆炸气泡运动进行模拟，将水面的变化的过程分为空穴形成、空穴塌落、气泡上浮出水、气泡射流和水柱回落五个阶段；张阿漫等基于BEM方法[5]，研究在不同距离、浮力、强度参数下气泡的脉动过程，对比各过程下的自由面的水冢现象。李健等采用等效初始气泡替代炸药的方式[6,7]，研究了近自由液面时的气泡膨胀过程和相对应的自由液面变化过程，研究了距离参数对自由面水冢变化的影响规律。Li等[8]、陈莹玉等利用物质欧拉求解方法及流固耦合技术[9]，研究气泡运动形态对水冢宽度与高都的影响。李帅等对皇冠型水冢的形成过程进行了模拟[10]，研究了水深距离、韦博数对皇冠型水冢特征参数的影响。Safiyari等基于SPH方法[11,12]，对爆炸气泡与自由液面的相互作用过程简化，将自由液面变化过程简化为空腔的扩张、坍缩，进而引起水面波动的过程，研究爆炸后自由液面的波动变化。李汪讳等将爆炸后自由液面的变化简化为锥形水柱的冲击水面的过程[13]。Wang等将气泡运动在水面附近形成的水冢简化为水下空腔和水面水柱两种形态[14]，对水面变化形态进行研究。

前人在研究气泡与自由液面相互作用时，大多考虑水深距离参数的对气泡脉动以及水冢形态的影响，较少考虑装药量的不同；在自由液面形态变化方面，主要关注于气泡运动对水冢形态的影响，在对水冢产生后的水面波动过程研究较少，对水面兴波过程的研究基本建立在水冢形态简化条件下。在实际工程中，水下爆破后水面将会产生一个持续的波动过程，且装药量的变化对水面运动形态的影响较大。基于此，采用ANSYS非线性有限元软件，基于ALE算法，结合水冢形成过程及其特征几何参数、气泡运动特性与水面波动过程，就不同装药量条件下，水下爆炸气泡运动对水面形态的影响机理开展研究。

1 水下爆炸气泡运动数值模拟

1.1 基于ALE方法的气泡运动模拟

采用ALE(Arbitrary Lagrangian-Eulerian)算法对气泡运动进行三维数值模拟，ALE算法具有在保持物质界面的同时防止网格过度变形造成计算失效的特点，该算法兼顾Lagrange算法与Euler算法的优点，在模拟爆炸产生气体的大变形现象的同时，保持对不同物质之间界面的捕捉，能较好地模拟水下爆炸过程中流体的大范围变形与气泡、水流的高速流动。

在ANSYS软件中进行数值计算时，为了提高计算效率同时保证模拟结果的正确性，在气泡最大半径1.5倍范围内采用与装药半径尺寸相同的均匀网格，其他区域采用由均匀网格区域至流域外边界逐渐渐变的网格。为了兼顾计算效率，采用三维1/4模型，在对称面上施加对称边界条件，在空气域和水域外边界处设置pressure outflow边界单元层，以模拟无限边界条件，模型的x/y方向和装药下方的水域深度应至少为气泡脉动最大半径的4倍，空气层的高度满足水冢中心水柱向上发展的要求。几何模型如图1。

炸药使用*MAT_HIGH_EXPLOSIVE_BURN材料模型，采用JWL状态方程

(1)

式中：p为爆轰产物压强,Pa；V相对体积,V=v/v0，v0为初始相对体积；e为单位体积内能,J/m3；A、B、R1、R2、ω为状态方程参数，见表1。

图 1 模型示意图Fig. 1 Schematic diagram of the model

水使用*MAT_NULL材料模型，采用Grüneisen状态方程

(γ0+αμ)E

(2)

式中：p为压强,Pa；ρ0为水体密度,kg/m3；C为水中声速；E单位体积内能,J/m3；V为相对体积；γ0、S1、S2、S3为GRUNEISEN状态方程参数，α为γ0的一阶体积系数；Pc为截断压强，Pa，水的截断压强为饱和蒸气压；η水的粘滞系数，Pa·S。水的材料方程与状态方程参数见表2。

空气使用*MAT_NULL材料模型，采用线性多项式状态方程

p=C0+C1μ+C2μ2+C3μ3+(C4+C5μ+C6μ2)E

(3)

(4)

表 1 TNT炸药的材料方程和状态方程参数取值[15,16]

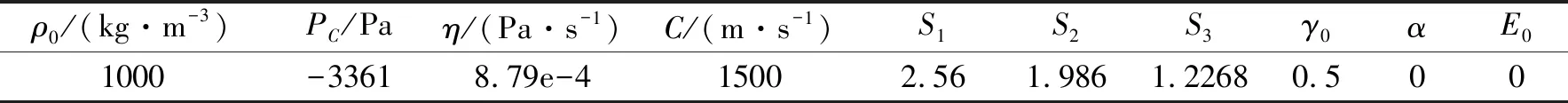
表 2 水的材料方程和状态方程参数取值[15,16]

对于理想气体有下列关系式

C0=C1=C2=C3=C6=0,C4=C5=γ-1

(5)

(6)

式中：p为压强,Pa；γ为单位热值率，对于理想气体γ=1.4；E0为单位体积初始内能；C0、C1、C2、C3、C4、C5、C6为线性多项式方程参数。空气的材料方程与状态方程参数见表3。

表 3 空气的材料方程和状态方程参数取值[15,16]

1.2 气泡运动模型的验证

为了验证气泡运动模型的有效性，设置与文献[17]实验相同的工况，使用5.2 g TNT的球形装药(与实验中4 g PENT炸药等效)，装药半径为0.009 m，模型计算尺寸为1 m×1 m×4 m，渐变网格划分尺寸最小为0.009 m，最大为0.1 m，均匀网格处网格尺寸为0.009 m。如图2所示，就文献中近水面条件(装药位置位于水面以下0.13 m)下的气泡运动趋势相对比，发现实验结果和数值模拟结果两者在气泡脉动的模拟结果，一致性较好。

对于TNT炸药水下爆炸气泡脉动的第一周期及气泡半径计算，已经形成了能够应用于工程实际的经验公式[17]。如表4所示，通将数值模拟结果与经验公式计算值进行对比，发现气泡半径及气泡周期变化误差在10%以内，表明数值模拟结果可靠。

图 2 近自由液面条件下气泡运动趋势对比Fig. 2 Comparison of bubble movement trends near free surface of water

(7)

(8)

式中:R为气泡第一次脉动的气泡最大半径,m；T为脉动周期,s；W为装药当量,kg；D为装药位置处水深,m。

表 4 气泡最大半径与周期误差计算结果

2 气泡运动对水面形态的影响

2.1 不同类型水冢形成过程与水面形态

不同水冢现象的发生取决于起爆点水深距离参数γf=h/Rmax[18]，式中：h为炸药装药位置距水面的距离,m；Rmax为气泡脉动过程的最大半径,m。那立民等通过大量工况计算[19]，总结出水冢形态与距离参数γf的关系，将水冢形态划分为零碎型(0≤γf≤0.06)、飞溅型(0.06≤γf≤0.03)、酒杯型(0.3≤γf≤0.7)、皇冠型(0.7≤γf≤1.4)等。为研究不同水深距离参数下水冢的形成过程，选用5 kg球型TNT炸药，控制炸药质量不变，改变炸药中心至水面距离，对四种特征水冢的形成进行模拟。模拟参数与结果如表5。

表 5 不同水深距离参数γf下的水冢形态

如图3所示，5 kg球形TNT炸药在水下爆炸的模拟结果表明，随着水深距离参数的不断增大，依次产生了零碎型、飞溅型、酒杯型及皇冠型等不同类型的水冢，且水冢所产生的空腔最大半径也在逐步增大，在酒杯型水冢空腔最大半径达到最大。

2.2 不同装药量对水冢形态的影响

皇冠型水冢形态较为稳定，以形成皇冠型水冢的特征水深距离参数γf=1作为基准参数，对不同装药量下水冢形态发展进行研究。表6所示，在0.5 kg、5 kg、50 kg装药量条件下，爆炸气泡脉动第一周期时间分别为186 ms、318 ms、665 ms。气泡第一周期时间与装药水深相关[17]，在同一距离水深参数条件下，不同装药量产生的气泡半径大小不同，需要的装药水深不同，气泡第一周期脉动时长不同。随着装药量增大，气泡脉动第一周期时长增加。

图 3 不同水深距离参数γf下的水冢形态Fig. 3 Water mound morphology under different water depth and distance parameters γf

表 6 不同装药量下气泡特征

为了对水冢形成过程进行直观对比，以当前时刻/气泡脉动第一周期时长对时间单位进行归一化处理。5 kg球形TNT炸药，在水深距离参数γf=0.998条件下将产生皇冠型水冢，如图4所示。水冢形态发展过程为：0.483时刻，气泡膨胀至最大半径，水面被气泡顶起；0.9时刻，由于气泡坍塌，形成向下气泡射流，并向上形成水射流，与气泡顶起的水体一起组成了中心水柱；1.317时刻，随着气泡射流发展的同时，向上水射流也在不断发展，并促进了中心水柱的发展。环形水体也在气泡膨胀的推动下开始突出水面向上发展，并与中心水柱一起构成了皇冠型水冢；2.4时刻，气泡经过多次脉动分裂成两个部分，水冢也在多次气泡脉动作用下形成了位置不同的环状水体；2.65时刻后，水面水柱达到最大高度，此时四周的水冢已经在重力作用下下坠，冲击水面并形成波动向外传播。

图5、图6分别为0.5 kg、50 kg装药量下水冢发展过程。在归一化1时刻，自由液面均形成中心水柱(图5d、图6d)，随后中心水柱与环形水体发展成为冠状结构(图5e、图6e)，该过程与5 kg装药量下皇冠型水冢的形成过程类似。对比图4、图5、图6可知，在相同水深距离参数条件下，装药量的增大并不会改变水冢的基本形态。

图 4 5 kg装药量，γf=0.998条件下水冢形态发展过程(a)～(i)为归一化时间Fig. 4 The development process of water spike morphology under the condition of γf=0.998 and charge amount of 5 kg((a)～(i) are normalized time)

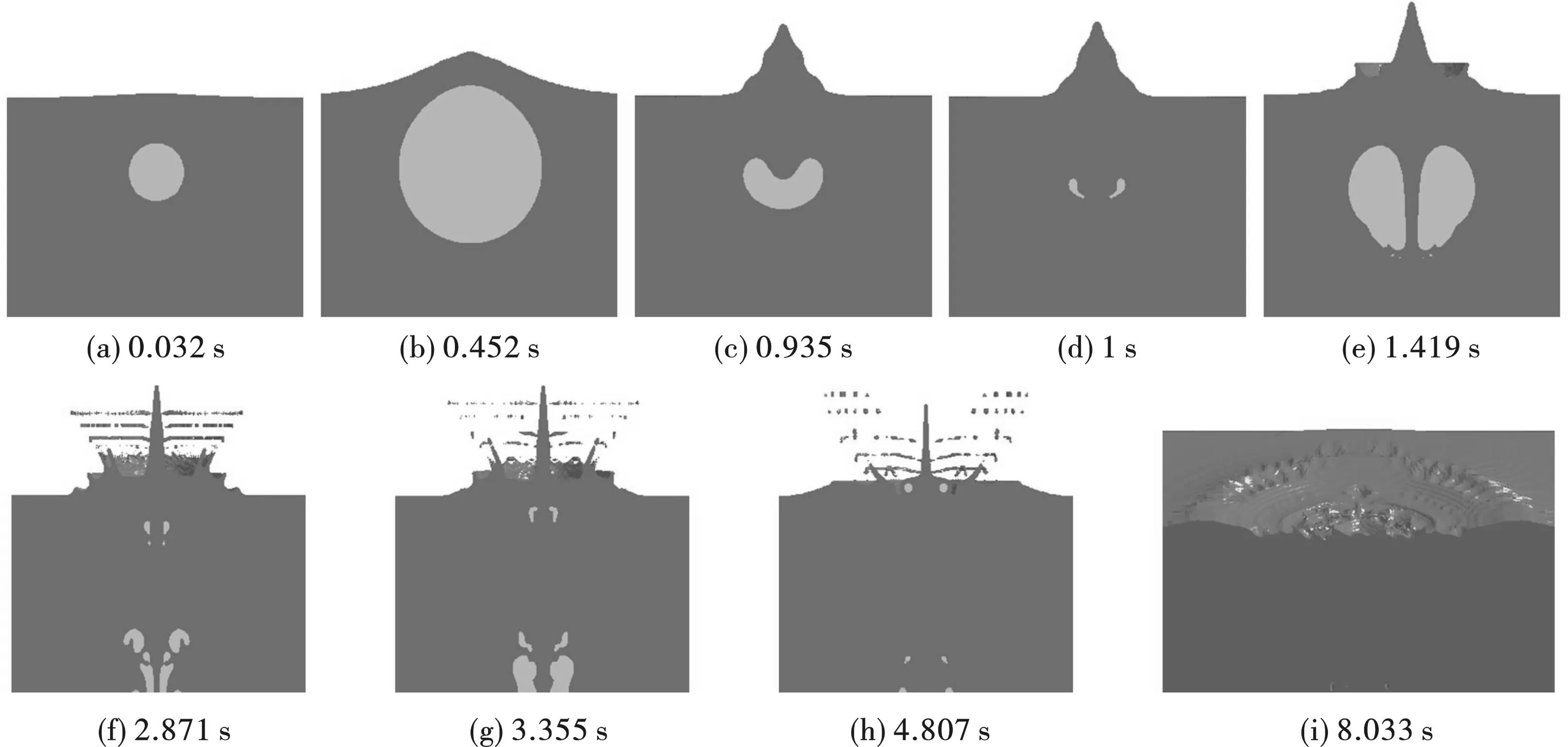
图 5 0.5 kg装药量，γf=1.003条件下水冢形态发展过程(a)～(i)为归一化时间Fig. 5 The development process of water spike morphology under the condition of γf=1.003 and charge amount of 0.5 kg((a)～(i) are normalized time)

图 6 50 kg装药量，γf=0.999条件下水冢形态发展过程(a)～(i)为归一化时间Fig. 6 The development process of water spike morphology under the condition of γf=0.999 and charge amount of 50 kg((a)～(i) are normalized time)

对比三种装药量下的水冢形成过程。在气泡脉动第一周期收缩阶段，0.5 kg、5 kg装药量下形成的收缩气泡呈现果仁状，产生向下的射流，同时水面形成向上的水射流，对应的归一化时刻分别为0.935 s(图5c)、0.900(图4c)；50 kg装药量下在气泡收缩过程中，在气泡的上表面形成了向下射流，下表面形成了向上射流，对应时刻为0.937 s(图6c)。在水冢冠状结构发展过程中，0.5 kg、5 kg装药量下形成多个不同位置的环状水体，对应时刻为2.871 s(图5f)、2.400(图4f)；50 kg装药量下形成的环状结构较为破碎，对应时刻为2.424 s(图6f)。

2.3 不同装药量对气泡运动的影响

对比图4、图5、图6，装药量增大使爆炸形成的气泡体积增大，气泡运动趋势发生改变。对不同装药量下的气泡运动特征进行对比分析，图7(a)为在归一化时间下的气泡时程变化曲线，气泡最大半径随着装药增大而增大。图7(b)为在归一化时间下气泡的无量纲位移(气泡中心位移/气泡最大半径)历程曲线，在第一周期膨胀阶段，三种装药量条件下的气泡中心均向自由面移动。在第一周期收缩阶段，0.5 kg装药量下气泡中心的向远离自由面方向移动；5 kg装药量下气泡中心位移基本稳定在初始位置附近；50 kg装药量下气泡中心始终向自由面移动。在张阿漫等对近自由面气泡运动规律研究中[5]，无量纲水深距离γf=1的条件下，气泡中心位移变化与浮力参数相关。可见在相同水深距离参数下，装药量的增大会使气泡最大半径增大，引起浮力参数的变化，从而产生不同的射流情况。在0.5 kg、5 kg装药量情况产生的气泡体积较小，自由面的Bjerknes作用力占主导地位，气泡在收缩阶段形成远离自由面方向的射流；而在50 kg装药量情况下，气泡体积较大受到的浮力作用增强，在收缩阶段气泡表面和底端均形成射流。

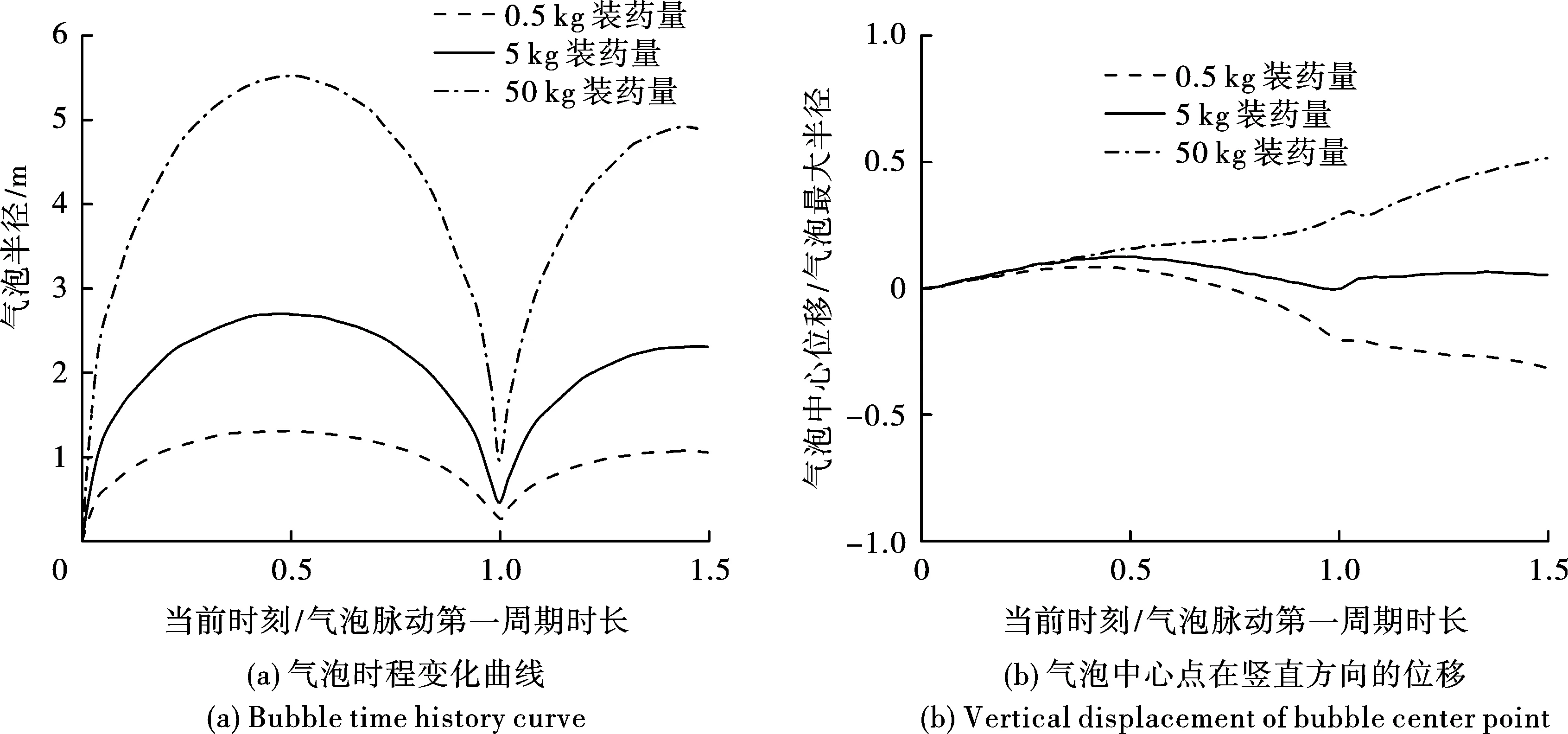
图 7 不同装药量气泡运动特征对比Fig. 7 Comparison of bubble motion characteristics with different charges

2.4 不同装药量下的水冢特征参数及水面波动对比

冠型水冢特征宽度为气泡脉动第二周期收缩至最小时刻形成的水冢底部宽度，特征高度为中心水柱最高点距自由液面高程的距离。对0.5 kg、5 kg、50 kg三种装药量下的计算结果进行了比较，如图8所示。在0.5 kg时水冢宽度为2.428 m，中心水柱高度为2.315 m；5 kg时水冢宽度为4.978 m，中心水柱高度为4.437 m；50 kg时水冢宽度为11.538 m，中心水柱高度为10.179 m。随着装药量的不断增大，水冢宽度、中心水柱高度逐渐增大。

图 8 不同装药量下水冢特征尺寸对比Fig. 8 Comparison of characteristic sizes of water mounds with different charges

在最大气泡半径2倍位置处设置监测点，对0.5 kg、5 kg、50 kg装药量下的水面波动特性进行分析，如图9所示。0.5 kg、5 kg、50 kg装药量在监测点处形成的最大水面波动高度分别为40.978 cm、53.636 cm、153.684 cm，随着装药量的增加，产生的水面波动在增大。对于50 kg装药量，由于气泡的上浮效应，能够托动更多的水体上升，冲击水面形成的水面波动最大高度也相对较大。在2时刻以内，水面波动由爆炸初期气泡顶起的水体产生，气泡半径将影响水面波动的大小。随着中心水柱以及环形水体的发展，监测点处自由液面先上升后下降，并随着中心水柱及环形水体的下坠冲击，出现波动状况。从图9中可看出，随着装药量增大，达到最大波动的时间在不断提前。经计算，水面波动从水域中心传播到2倍气泡半径处的平均速度分别为1.985 m/s、2.894 m/s、3.533 m/s，由于水面中心水柱和环状水体所具有的势能大小不同，从而影响了水面波动到达测点的时间。随着装药量的增加，水面波动高度在逐渐增大，且水面波动达到最大的时刻也在不断提前。