CEEMDAN-小波阈值法在爆破振动信号处理中的应用

2022-09-20费鸿禄

爆破 2022年3期

费鸿禄，山杰

(辽宁工程技术大学爆破技术研究院，阜新 123000)

爆破振动信号分析是矿业、岩土等工程界研究爆破振动效应的的主要方法，但在施工现场采集的的样本信息中，受施工现场复杂环境的影响，采样信息中含有大量高频噪声，同时还受到信号采样仪器松动或者温度变化产生零点漂移的情况，采样信息可能会出现形状不规则和基线偏移情况，即采样信息中产生了趋势项[1]。两者共同作用导致采样信号失真，使爆破信号时频能量的进一步分析产生较大误差。因此，采样信号的去噪及趋势项处理就成了不可或缺的前处理工作。

目前，国内外常用的爆破振动信号的去噪方法主要有小波阈值去噪[2]、小波包阈值去噪[3]、经验模态分解(empirical mode decomposition，EMD)方法[4]、集合经验模态分解(ensemble empirical mode decomposition，EEMD)方法[5]、互补集合经验模态分解(complementary ensemble empirical mode decomposition，CEEMD)方法[6]，以及两者共同使用的EMD-小波阈值法[7]、EEMD-小波阈值法[8]、CEEMD-小波阈值法等[9]。小波类方法对不同的频率成分提供不同的分析分辨率，同时在时频域的局部化性质中有明显优势，在非平稳信号处理中备受青睐，但存在小波基难以选取，分解层数难以确定的缺点。目前对信号的趋势项消除方法主要有EMD法[10]、EEMD法[11]、变分模态分解(variational mode decomposition，VMD)法等[12]，而同时对两者进行处理的方法中[13,14]，EMD方法主要问题为端点效应和模态混叠，EEMD方法虽然避免了EMD方法端点效应和模态混叠现象，但同时引入了均匀分布的白噪声。CEEMD方法通过加入一对互为相反数的辅助白噪声解决EEMD方法存在的白噪声问题，但处理本质没变，分解结果难免受到残余白噪声影响。自适应噪声完备集合经验模态分解(complete ensemble empirical mode decomposition with adaptive noise，CEEMDAN)方法是从EMD的基础上加以改进[15]，同时借用了EEMD方法中加入高斯白噪声和通过多次叠加并集成平均以抵消噪声的思想，能减轻端点效应和模态混叠现象，避免残余噪声影响，但处理效果还是不够理想，容易丢失部分真实信息。

为解决CEEMDAN分解丢失信息以及小波基难以选取、分解层数难以确定的问题，将自适应噪声完备集合经验模态分解(CEEMDAN)和小波阈值法的优势结合起来，辅以频谱筛选并去除趋势项、互相关与自相关函数分析与校核噪声分量，提出了一种处理爆破振动信号趋势项与高频噪声的方法，对爆破振动响应研究具有重要意义。

1 爆破振动信号处理理论

1.1 CEEMDAN分解原理

EEMD、CEEMD分解方法是将添加白噪声后的信号直接做EMD分解，然后相对应的IMF分量直接求均值。CEEMDAN算法是每求完一阶IMF分量，又重新给残余分量加入正态分布的高斯白噪声并求此时的IMF分量均值并逐次迭代。其详细实现过程如下[16]：

(1)将标准正态分布的高斯白噪声wi(t)加入到爆破振动信号x(t)中，则待处理信号变为x(t)+ζ0wi(t)。使用EMD方法对待处理信号进行I次重复分解后对其进行算数平均可得到IMF1分量为

(1)

去除第一阶分量IMF1后的残余分量

r1(t)=x(t)-IMF1(t)

(2)

(2)定义从待处理信号的EMD分解中获得的第j个模态函数分量的算子为Ej(·)。再次将标准正态分布的高斯白噪声wi(t)加入到分量r1(t)中，则对信号r1(t)+ζ1E1[wi(t)]再次通过EMD方法进行I次重复分解，可得到IMF2分量为

(3)

去除第二阶分量IMF2后的残余分量

r2(t)=r1(t)-IMF2(t)

(4)

(3)对于k=2,3,…,K，去除IMFk分量后的残余分量为

rk(t)=rk-1(t)-IMFk(t)

(5)

(4)提取信号rk(t)+ζkEk[wi(t)]的第一个IMF分量，定义k+1个模态函数分量为

(6)

(5)重复执行步骤(3)和(4)，直到残余分量信号不可再继续被分解为止，最终可以得到K个模态函数分量。

原始爆破振动信号可以表示为

(7)

式中，R(t)为最终残余分量。

从上述CEEMDAN的基本理论可以看出，此方法在较小的平均次数下就可以有很好的完备性与模态分解结果，计算速度上也有明显优势，且可以改变每一阶段的噪声系数ζi，自适应的选择不同信噪比的高斯白噪声。

1.2 小波阈值方法

小波阈值法去噪的本质是对信号的滤波。小波阈值法是先通过小波变换把信号转换为不同尺度的尺度空间，然后通过阈值处理筛选出噪声并过滤掉噪声，最后再重构信号。小波阈值法在爆破振动信号滤波去噪中，阈值处理至关重要。阈值处理包括阈值选择与阈值函数选择。目前阈值选择方法有4种，RigSure阈值、Heursure阈值、Sqtwolog阈值、Minmax阈值。常用的阈值量化规则一般分为硬阈值与软阈值，硬阈值函数处理信号后会在阈值λ处产生局部突变。软阈值函数处理得到的信号虽然丢失了一小部分高频信号，但信号更平滑，消除了硬阈值函数处理引起的局部突变。

小波去噪硬阈值处理函数

(8)

小波去噪软阈值处理函数

(9)

式中：w为小波系数；λ为阈值。

1.3 CEEMDAN-小波阈值处理方法

CEEMDAN-小波阈值方法先将爆破振动信号进行CEEMDAN分解处理，在判断出趋势项分量后，对剩余IMF分量进行互相关系数和自相关函数分析确定噪声IMF分量，对其进行小波阈值处理过滤掉噪声信息，提取CEEMDAN分解丢失的部分有效信息。最后，将小波阈值滤波处理后的IMF分量与纯净IMF分量重构得到处理后信号。完整流程如图1所示。

图 1 信号处理流程图Fig. 1 Signal processing flowchart

2 工程实例分析及效果评价

选取武家塔露天矿实测的某次爆破振动径向信号，如图2所示。可以看出该信号由于现场环境复杂受到较多噪声污染且有很明显的趋势项情况，信号波形偏离基线中央，出现失真情况。为了不影响信号时频能量的进一步分析，需要对其进行处理。

2.1 CEEMDAN分解

通过反复实验，加入白噪声的噪声标准差与振动径向信号标准差的比值(幅值)为0.2，信号的平均次数为100，最大迭代次数为2000时，CEEMDAN分解处理效果最好。11个IMF分量(IMF1～IMF11)和一个残余分量Res由原始爆破振动径向信号通过CEEMDAN分解得到，结果如图3所示。

图 2 振动径向信号Fig. 2 Vibration radial signal

2.2 振动信号处理

2.2.1 趋势项处理

对各个IMF分量进行FFT(Fast Fourier Transfer)变换，得到各个IMF分量的主频，结果如表1所示。由于趋势项为低频干扰，对疑似趋势项IMF9、IMF10、IMF11和Res分量进行频谱主频带分析，结果如图4所示。从图4可以看出，IMF11、Res分量的频带主要集中分布在0～5 Hz的低频范围内，且主频低于爆破测振仪监测的有效范围(2～200 Hz)，可能为零漂或信号变化趋势[17]。相比之下，IMF9、IMF10频带更宽，主频在有效监测区间之内，因此去掉IMF11、Res趋势项分量。

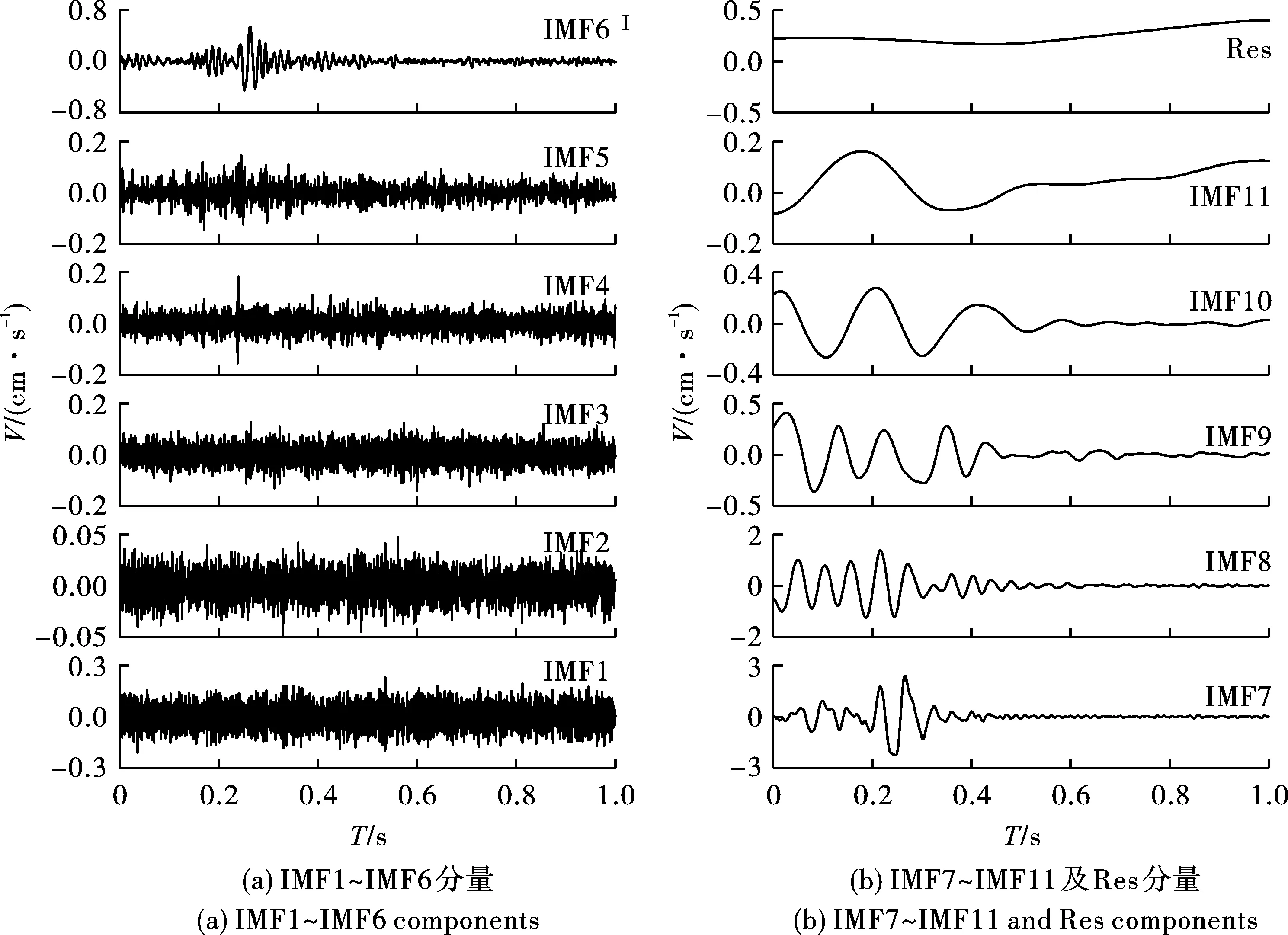
图 3 CEEMDAN分解结果Fig. 3 CEEMDAN decomposition results

表 1 各主频对应表

图 4 疑似趋势项频谱Fig. 4 Spectrum of suspected trend items

2.2.2 噪声处理

将剩余IMF分量与振动径向信号通过MATLAB中的corrcoef函数求出互相关系数R，结果如表2所示。从表2可以看出IMF1、IMF2、IMF3、IMF4和IMF5分量的互相关系数均小于0.1，初步认定为含噪IMF分量[18]。针对IMF1、IMF2、IMF3、IMF4和IMF5疑似高频噪声分量，通过MATLAB中的xcorr函数对其进行自相关函数分析，结果如图5。

表 2 剩余分量互相关系数对应表

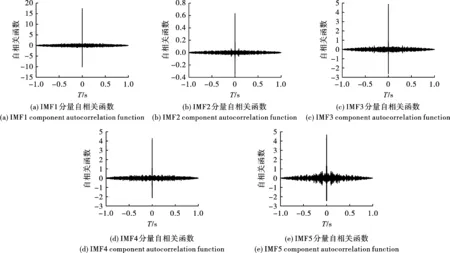
图 5 疑似噪声分量自相关函数Fig. 5 Autocorrelation function of suspected noise component

从图5(a)～(d)分析可知，分量IMF1～IMF4在零点处的自相关函数达到最大值，其他时间的自相关函数趋近于0，因此定义分量IMF1～IMF4为高频噪声分量[19]。由图5(e)可知，IMF5分量虽然在零点处自相关函数为最大值，但其余时间处并不完全符合噪声特性，由表1也可知IMF5分量主频为180.7 Hz，主频在有效监测区内，因而IMF5分量同时也包含了一些信号的有效信息，需要对其进行小波阈值滤波去噪处理。由于本文中爆破测振仪器设置的最小采样频率为2 Hz，根据采样定理[20]，设置的采样频率为4000 Hz，奈奎斯特频率为2000 Hz，选取小波基函数“db8”对IMF5分量进行8层分解，其最低频带为0～7.8125 Hz。选取基于Stein的无偏移风险估计原理获得小波阈值和具有光滑性的软阈值函数进行滤波去噪处理。

2.3 波形重构

将纯净IMF分量与滤波去噪处理后分量叠加得到处理后信号。处理(去除趋势项及噪声)前后信号波形及频谱如图6和7所示。分析图6可知：处理后的信号波形回到基线中央，曲线更加光滑，消除了噪声污染影响，保留了信号真实信息。此外，由图7(a)可知，处理前的信号频谱低频段存在突高的相对幅值，高频段存在明显的噪声相对幅值，严重影响了信号频谱分析的准确性。由图7(b)可知，处理后的信号在0～2 Hz低频段较大相对幅值已经消除，表明去趋势项效果显著。2～200 Hz频段振动信号无明显变化，表明处理方法消除噪声干扰外，并不会影响信号的真实信息，而200 Hz以上频段相对幅值基本为零，说明处理方法去除了高频噪声污染。

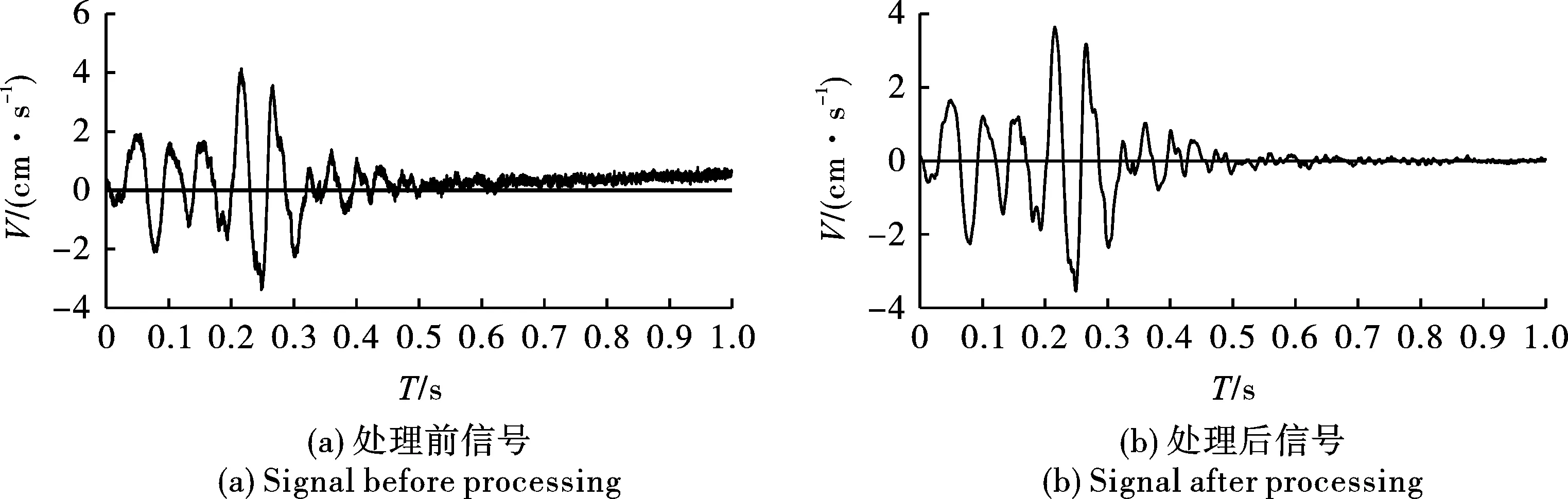
图 6 处理前后信号波形Fig. 6 Signal waveform before and after processing

图 7 处理前后信号频谱Fig. 7 Signal spectrum before and after processing

2.4 对比分析

为了反应处理方法的效果，将信噪比(SNR)、均方根误差(RMSE)作为处理效果的衡量指标，一般认为SNR越大，RMSE越小，其处理效果越好。其计算公式如下

(10)

(11)

式中：Xi为处理前信号；xi为处理后信号；N为信号长度。

将本文处理方法与单纯的CEEMDAN方法、小波阈值方法以及EMD-小波阈值法、EEMD-小波阈值法和CEEMD-小波阈值法在衡量指标上进行对比，对比结果如表3。

从表3可以看出，在信噪比方面，CEEMDAN方法、小波阈值法与本文方法相比，本文处理方法最高，CEEMDAN方法次之，小波阈值方法最小，说明CEEMDAN方法处理不够理想，容易丢失部分真实信息，而小波阈值处理效果不如其他两种方法。本文较EMD-小波阈值法、EEMD-小波阈值法和CEEMD-小波阈值法相比信噪比也有所提高，说明本文处理效果更好；在均方根误差方面，CEEMDAN-小波阈值法较其他几种方法相比也显示出更好的可靠性与稳定性。综上所述，经过与目前广泛采用的多种信号处理方法比较，本文应用的CEEMDAN-小波阈值处理方法最优。

表 3 衡量指标对比

为了进一步反映CEEMDAN-小波阈值方法的处理效果，使用Hilbert变换获得时间、频率和能量的三维图来反应处理前后的变化情况。处理前后的三维图如图8所示。

图 8 处理前后三维图Fig. 8 Three-dimensional image before and after processing

从图8(a)分析可知，由于趋势项的干扰，源信号在0～0.6 s的高频段(2000Hz左右)以及0.6～1 s的低频段(0～2 Hz)出现较大能量的分量，而由于噪声干扰，在200～2000 Hz频段上也出现了较小的噪声能量，这就导致了信号的失真，从而增大爆破振动信号分析的误差甚至致使其结果严重不符合实际。从图8(b)可以看出，上述由于趋势项和噪声引起的能量分量通过CEEMDAN-小波阈值方法处理后被成功剔除，而0～200 Hz频段能量没有明显变化，说明CEEMDAN-小波阈值方法不仅能消除趋势项和噪声干扰，而且对2～200 Hz频段能量信息保留完整。