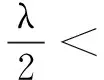高中数列问题中的“陷阱”
2022-09-19阮联玉
阮联玉
(陕西省丹凤中学,726200)
数列问题在高考中考查越来越灵活,其难度适中,但学生却常常很难得满分.究其原因,多数是解答时忽略条件,踩中“陷阱”.本文就高中数列问题中的常见丢分点进行归纳,分析其原因,找到应对策略,希望能给学习者一个提醒和帮助.
一、条件不等价,掉入“陷阱”
例1在等比数列{an}中,已知a5+a1=34,a5-a1=30,则a3=( )
(A)8 (B)-8 (C)±8 (D)16
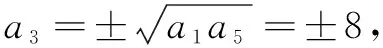
正解由题意可解得a1=2,a5=32,因为数列{an}为等比数列,所以32=2q4,解得公比q=±2.又因为a3=a1q2=8,所以选A.
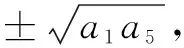
变式题在等比数列{an}中,已知a2 012=4,a2 024=16,则a2 018=______.(参考答案:8)
例2等比数列{an}的前n项和为Sn,S2=7,S6=91,则S4=( )
(A)28 (B)32
(C)-21 (D)28或-21
错解由等比数列前n项的和性质,得S2,S4-S2,S6-S4也成等比数列,所以(S4-S2)2=S2(S6-S4),得S4=28或-21.选D.
正解同上解得S4=28或-21.
因为S4=a1+a2+a3+a4=a1+a2+a1q2+a2q2=(a1+a2)(1+q2)=S2(1+q2)>0,所以S4=28.选A.
二、讨论不全面,掉入“陷阱”
例3求和Sn=x+2x2+3x3+…+nxn.
错解由通项公式可以看出该数列是等差数列乘以等比数列,可用错位相减法求和.
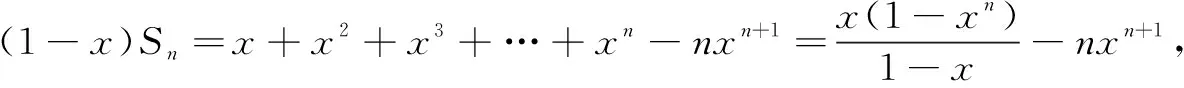
正解当x=0时,Sn=0.
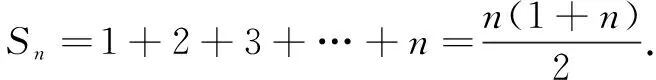
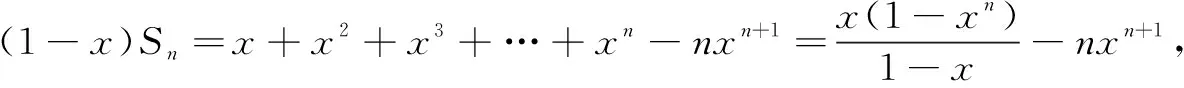
综上,可得
评注在含字母的数列中,一定不能忘了字母是否为零的情况.在等比数列求和时,一定不能忽略对公比是否为1的情况,注意进行讨论.
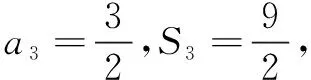

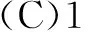
(参考答案:B)
三、数不清项数,掉入“陷阱”
例4和式1+4+7+10+…+(3n+7)=( )

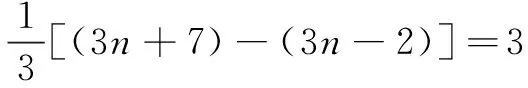
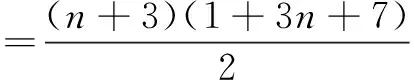
可知选C.
评注给n取数值代入通项公式,若与第一项不相同,说明就不是前n项的和.求出等差数列的通项,与题中最后一项作差,再除以公差,可明确多出的项数.
四、首项找不对,掉入“陷阱”
例5已知数列{an}满足a1=1,an+1=2an+1,求通项公式an.
错解因为an+1+1=2an+2=2(an+1),所以{an+1}是公比为2的等比数列.首项a1=1,故an+1=2n-1,可得an=2n-1-1.
正解因为an+1+1=2an+2=2(an+1),所以{an+1}是公比为2的等比数列.由于等比数列的首项是a1+1=2,所以an+1=2·2n-1,得an=2n-1.
评注构造新的数列后,新数列的首项是n取1时整个式子的值,而不再是原来数列的首项a1.为了避免错误,也可以换元,用整体思想比较好理解.
五、单调性理解错误,掉入“陷阱”
例6已知数列{an}满足an=n2-λn,若数列{an}为单调递增数列,则λ的取值范围是______.
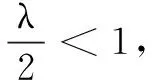

正解2由数列单调性的定义可得an+1>an,所以(n+1)2-λ(n+1)>n2-λn,即λ<2n+1对任意n∈N*成立,所以λ<3,得λ的取值范围为(-∞,3).