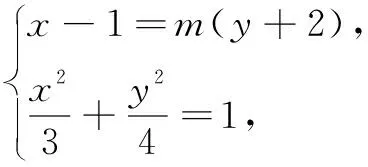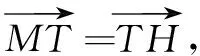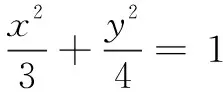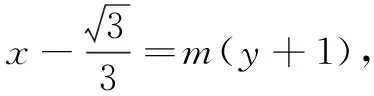一道圆锥曲线压轴题的解法探究

王昌林 罗萍双

(四川电影电视学院实验中学，611331)

一、试题呈现

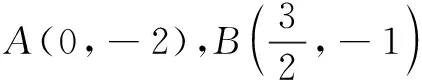
(1)求E的方程;

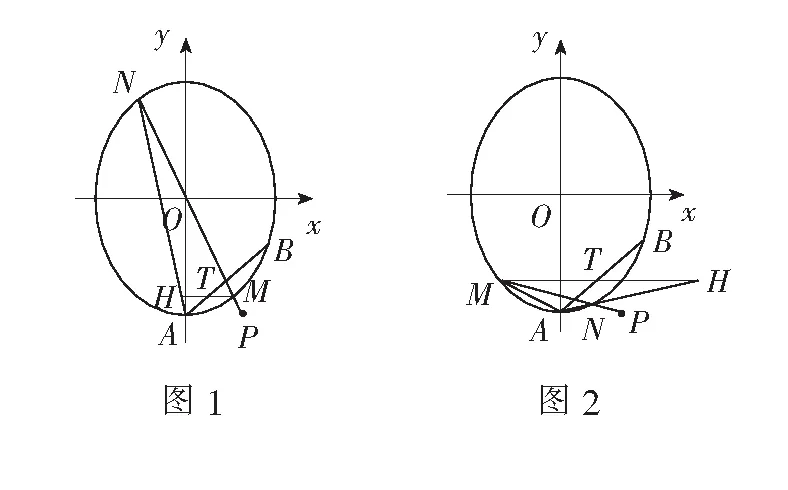
二、解法探究

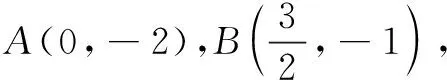
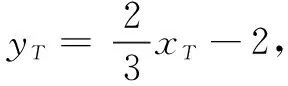
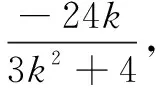
综上,直线HN过定点A(0,-2).

评注解法1是求解通法,但要对直线斜率是否存在进行讨论,过程较繁琐.改变直线方程的设定方式,可得如下解答.

解法2设点M(x1,y1),N(x2,y2),直线MN的方程为x-1=m(y+2).

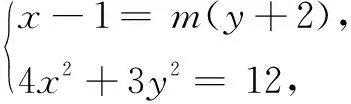
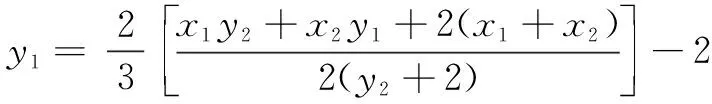
①

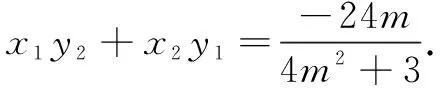
评注将直线方程设为x=my+n形式有效避免了对直线斜率的讨论,但运算过程仍较为复杂.究其原因在于椭圆方程的“不特殊”,若是将椭圆移动到较为特殊的位置是否方便计算呢?由此产生以下解法3的解答过程.

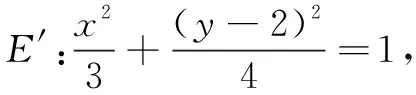
3y1y2=x1y2+x2y1.

②

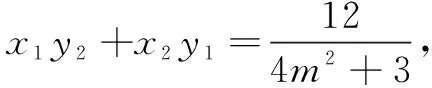
评注将椭圆进行平移后,整个解答过程无论是计算量还是式子的复杂程度都明显有了一定的简化.回顾解法2与解法3,将直线方程设为x=my+n可以有效简化解答过程.

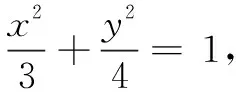
评注将直线方程用参数形式也是解决直线与圆锥曲线问题的常用方法.由本解法的特殊性,想到借助向量验证A,H,N三点共线,此外还可以借助斜率相等进行证明,因此产生如下解法.