一道椭圆问题的还“圆”处理*

刘晓丽 刘 银

(江苏省镇江市第一中学,212003)

圆是最美的几何图形,它既是轴对称图形，又是中心对称图形.

将圆进行某种伸缩变换可以得到椭圆;反之,椭圆可以看成由圆经过伸缩变换变形而成.因此,圆与椭圆血脉相通，二者之间有着诸多相似的性质.若能将椭圆上的一些几何关系等价转化到圆上,复杂问题往往会变得柳暗花明.本文运用转化与化归思想,将涉及椭圆的一道有关三角形面积的最值问题转换为圆中对应三角形面积的最值问题,展示椭圆问题“还原”成圆来进行简便处理时具备的神奇功效.

一、问题呈现

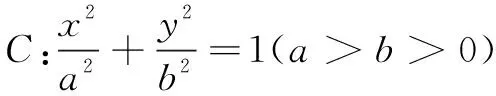
(1)求椭圆C得方程;

(2)直线l与椭圆C交于点P,Q,线段PQ的中点H,O为坐标原点,且OH=1,求∆POQ面积的最大值.

本题以直线和圆锥曲线为背景,属于考查圆锥曲线的常见题型,综合性较强,能较好地反映学生的逻辑思维能力、基本运算求解能力和几何直观等核心素养.

二、突破求解

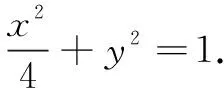
对于第(2)小问,从题型上看考查的是解析几何中三角形面积的最值问题,实质为求函数最值问题,求解的关键在于设参数建立函数关系式.根据本题条件求∆POQ的面积,应把目标放在确定底和高上.根据已知条件可以选择以OH为底,点P,Q到直线OH的距离为高;或将底建立在坐标轴上,以点P,Q横(纵)坐标差为高,进而求得三角形面积,建立函数关系式,这是学生容易想到的常规解法.但如果能稍微变换一下思维,把涉及椭圆的问题还原到圆中,会有意想不到的效果.

解如图1,以椭圆C的长轴为直径作圆O:x2+y2=4,分别过点P,Q作直线PA,QB平行于y轴,交圆O于点A,B.则依题意可得

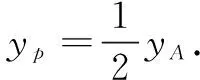
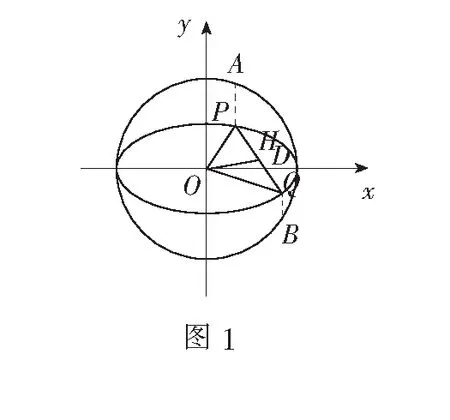
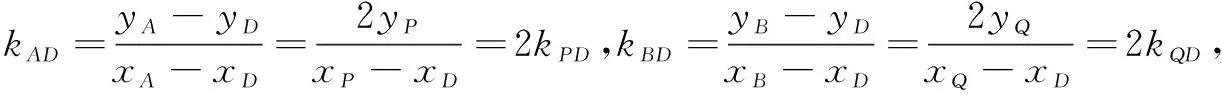
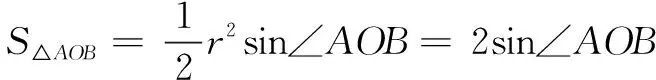
综上,∆POQ面积的最大值为1.

评注本题也可以将椭圆长轴横向压缩,将已知条件等价转化到圆上，解法类似.本解法具有高等几何伸缩变换的高数背景,是高观点下的初等解法,特别是伸缩变换保持三点共线关系的解释生动形象,易于被中学生接受.

三、教学思考

优化解题过程是提高解析几何解题速度和准确性的良方.上述解法采用数形结合和仿射变换思想,巧妙地将圆和椭圆有机结合,使人赏心悦目、耳目一新.上述解法计算量小,但思维量大,尤其对“点D也在直线AB上”的把握有难度.对于常规解法,很多同学有思路、有想法,但由于运算繁琐只能放弃.葡萄甜不甜,只有吃过才知道.课堂教学不能只分析思路、指出方法的可行性,尝试——失败——再尝试——再失败——直到成功,这样的过程让学生收获到的远比一道问题的解法来得更多.所以,我们一方面应将具体运算过程展示给学生,帮助学生提升各运算节点的处理策略,进而优化解题过程;同时另一方面也要帮助学生树立信心,无论走哪条路径,选定目标后可以坚持“算”下去.但在动笔“算”之前,应该先通过数学直觉预估一下解题成本和解题风险,考虑所选参数和路径的繁冗程度,最后盯住目标,抓问题本质,坚持就是胜利.

圆锥曲线是高中数学学习的难点,也是重点.圆锥曲线是解析几何的核心内容,也是高考内容的必考之一.若想快速找到合适的解决方法,平时学习过程中要多思、多练、多算,考场上才能游刃有余.蜜蜂采蜜不怕千辛万苦,学子求学何惧算个最值.