激光诱导前向转移中传输过程对银浆薄膜均匀度影响研究
2022-09-17陈炀单译琳杨倬波李海张宪民
陈炀,单译琳,杨倬波,李海,张宪民
(华南理工大学广东省精密装备与制造技术重点实验室,广东广州 510000)
0 前言
激光诱导太阳能正面电极化是指利用激光诱导前向转移原理(Laser Induced Forward Transfer,LIFT),将银浆转移至太阳能硅片正面形成栅线的过程。激光诱导前向转移技术是一种高精度、非接触式、无需掩膜的数字化印刷技术,其激光诱导高黏度浆料转移原理如图1所示。目标材料以薄膜的形式涂膜在透明基片上,以薄膜面朝硅片并使透明基片和硅片保持一定距离。激光透过透明基片聚焦于银浆薄膜上,银浆在吸收激光的能量后会形成高温高压的气泡,该高压气泡会持续膨胀并推动薄膜粘附至硅片,最终在银浆薄膜和硅片间形成桥式结构。待透明基片垂直移去后,银浆桥式结构会断裂,并在硅片上获得银浆。作为一种非接触式的转印技术,LIFT能有效避免对硅片的施压,从而避免硅片的破碎。另一方面,激光诱导转印技术无需掩膜,也就不存在堵塞的问题。因此,将激光诱导转印技术应用于太阳能电池电极制备极具前景,是当前该领域的研究热点。

图1 LIFT基本原理
目前国内外针对激光诱导高黏度银浆转移的研究并不多,MUNOZ-MARTIN等研究了激光诱导高黏度浆料点转移的机制,并发现当转移以生成银浆桥的模式进行时,所获得的转移点形状最规则,具有最高的高宽比。CHEN等讨论了激光诱导高黏度浆料线转移的可能性,并成功印刷了连续的银浆线,但印刷银浆线宽度为80~120 μm且呈现波浪状。SHAN等通过大量实验,研究了激光能量密度、间隙距离、银浆黏度、光斑尺寸以及光斑间距对栅线印刷质量的影响,最终根据优化后的参数成功印刷出宽度为44 μm、高宽比0.54的栅线。
根据上述实验的结论,能量密度、间隙距离、银浆黏度、光斑尺寸以及光斑间距等参数的变化都会对最终的印刷结果产生不同程度的影响。对于激光诱导太阳能电池电极印刷设备而言,能量密度、光斑尺寸以及光斑间距都能通过激光器系统来稳定控制,而银浆黏度也可以在进行印刷生产前调整,间隙距离则可以通过垫片或是机械结构进行控制。然而,银浆薄膜从成型到印刷至少需要经历3个步骤:喷料,刮涂,印刷。图2所示为设备的两种银浆运输模式,在设备实际工作中,玻璃底部可贴一定厚度耐磨胶,与刮刀配合形成相应厚度薄膜。但在运输过程中,薄膜的形貌会随玻璃的运动发生改变,且薄膜两侧的耐磨胶形成的壁面厚度有限,玻璃运动时极有可能会使银浆溅出。若玻璃通过如图2(a)所示的多工位转台旋转的方式进行工位切换,整体运行效率会比图2(b)所示的直线运输快很多,但此时银浆薄膜会同时承受切向作用力和法向作用力,流变更复杂。而银浆薄膜的形貌对激光诱导前向转移这一成型工艺而言影响巨大,探究不同运动规律下薄膜的变化情况非常必要。

图2 两种银浆薄膜运输方式
对银浆薄膜建立有限元模型,然后分别对直线运输与旋转运输情况下的银浆薄膜进行仿真,观测运输过程对薄膜均匀度的影响。进一步,针对直线运输情况,选择线性加速、指数形加速、S形加速3种常见电机加速曲线进行研究。仿真结果表明:将同样的速度施加在旋转运动时,由于离心力的存在,法线方向上的影响比切向方向更加明显;直线运动时,线性加速曲线下薄膜的变化最小。因此,在设计设备时,应尽量采取直线运动下线性加速模式。
1 银浆薄膜有限元模型及其均匀度评价指标
本文作者采用有限元法对银浆薄膜进行流体分析,考虑到流体仿真的复杂性,需要对模型进行必要的简化,将长宽相等的立方体银浆薄膜简化为如图3所示的运动模型,将薄膜四周设为壁面模拟耐磨胶。计算时采用流体体积法(Volume of Fluid,VOF)多相模型,以一定厚度的银浆和空气组成计算区域。 VOF方法是在整个流场中定义一个函数,在每个网格中,这个函数定义为一种流体的体积与网格体积的比值。只要求得每个网格上的值就可以构造出运动界面,求解物理方程时可以在界面附近作特殊的精细处理以提高分辨率和精度。银浆固含量较高,主要由银或其化合物、助熔剂、黏合剂和稀释剂配制而成,其流体性质为非牛顿流体,并且是一种假塑性流体。假塑性流体的流变特性常用如下的指数函数方程描述:

图3 三维仿真模型

(1)

在有限元软件中进行流体仿真时,对假塑性流体一般使用carreau黏性模型,采用式(2)计算流体黏度:

(2)
式中:为幂律指数;为时间常数;为零剪切黏度;为无限剪切黏度。银浆的相关参数选取数据由银浆厂商提供,如表1所示。考虑到实际工作中银浆薄膜厚度相对薄膜长度数量级差距较大,为减少网格划分与计算时的困难,在图4所示的0.05 mm厚、1 mm×1 mm的银浆薄膜上进行仿真,网格划分如图4所示,软件统计出模型共1 760 059个单元格,2 975 069个节点。通过编译用户自定义功能文件(User Defined Functions,UDF),让区域实现相应的运动方式。

表1 银浆参数

图4 网格划分
当区域进行直线运动时,可将模型简化为如图5所示的二维模型,此时可采用区域运动后薄膜基准面与水平面夹角和薄膜相对基准面的粗糙度两个指标来表征薄膜变化情况,图5为薄膜运动后的示意。薄膜在运动时整体会发生倾斜并且表面产生不规则变化,通过拟合薄膜表面得出倾斜后的基准面与水平面的夹角,能够表征运动后银浆薄膜相比运动前的状态保持程度;通过公式(3)计算出相对于基准面的算术平均高度,来表示粗糙度,以表征薄膜的均匀程度。为能够相对精确地模拟薄膜表面并计算夹角和粗糙度,文中所有导出的银浆薄膜表面坐标指的都是银浆体积分数在(0.9,1)之间的点坐标。

图5 银浆薄膜示意

(3)
2 不同转运模式及速度下的银浆均匀度变化仿真研究
2.1 仿真方案介绍
考虑到银浆薄膜的自愈特性,需在它停止运动后一定时间内观察薄膜的变化情况,得出合适的薄膜观测时间。对直线运输和旋转运输两种运输方式在三维模型中进行仿真,观察银浆薄膜的变形,选择出合适的运输方式。对该运动方式在3种不同的加速曲线(线性加速,指数形加速,S形加速)下进行仿真,观察银浆薄膜的变形,选择合适的电机加速规律。
2.2 银浆薄膜自愈性仿真
由于黏性流体的自愈特性,银浆薄膜运动产生变形后静置的一段时间内,银浆会有恢复其原本薄膜形态的趋势而产生的小变形,因此需待它完全停止变形后,再观察形貌。为得出合适的薄膜观察时间点,进行以下仿真实验:给二维模型一个不同大小的速度令它进行直线运动,并在经过0.1 s后线性减速为0,从运动结束时刻起导出银浆表面坐标并计算其夹角和粗糙度随时间的变化情况如图6所示。可以看到:尽管由于速度越大导致运动停止后的变化越大,但银浆薄膜变化都集中在0.1~0.2 s之间,即运动停止后的0.1 s内;其中=5 m/s时夹角的变化达到12.01%,粗糙度的变化达到16.00%,而在0.2 s之后,两者都趋于平稳,夹角和粗糙度几乎没有变化。综合考虑,文中所有仿真将直接采用运动停止后0.1 s时刻作为薄膜停止变形的时刻并进行观察比较。
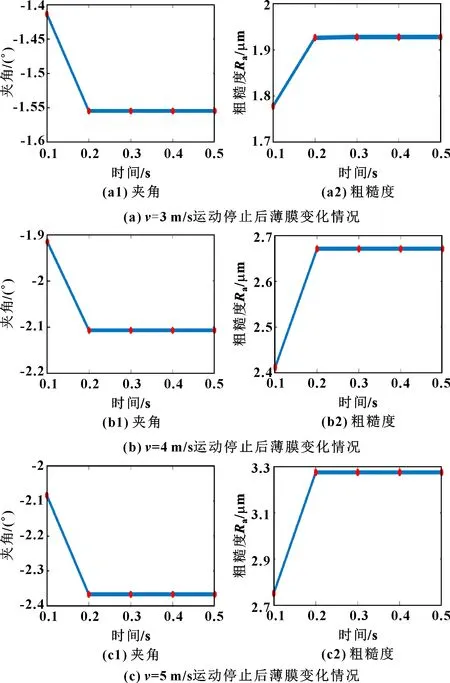
图6 在不同速度运动停止后薄膜随时间变化情况
2.3 不同转运模式对比仿真研究
令速度=3 m/s,使三维模型沿轴正方向进行匀速直线运动,同时以模型下壁面中点为旋转中心,令薄膜中心的切向速度=3 m/s作用于三维模型进行顺时针旋转运动,在运动1 s后将两者仿真结果沿轴每隔0.1 mm取一截面,将每个截面的薄膜表面点坐标导出,并将所有点拟合曲面作为薄膜表面,如图7所示。
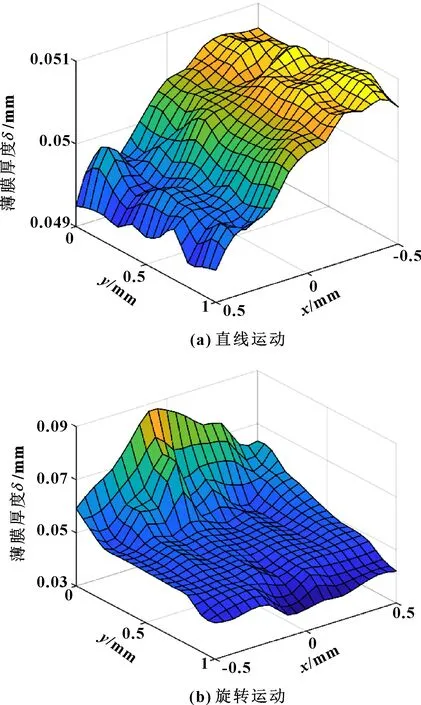
图7 薄膜表面拟合结果
由图7可知:对于直线运动,由于方向正方向速度的影响,银浆厚度沿轴负方向整体呈略微上升趋势,薄膜大部分厚度在0.049~0.051 mm之间,整体均匀性较好,而沿轴方向整体无明显变化,同时也验证了将三维模型简化为二维模型的合理性;对于旋转运动,薄膜受离心力影响明显,法向方向的变化远大于切向方向的变化,而且在距离旋转中心最远的薄膜外层呈现凸起状,最大厚度约为0.09 mm,说明中间受到的影响比两侧要明显。但薄膜中间部分整体相对均匀,厚度在0.04~0.06 mm之间,可以考虑增大薄膜面积,对中间相对均匀的部分进行转移。
2.4 不同速度曲线下的仿真研究
如图 8所示,在相同的运动时间与位移下,以电机常用的3种速度变化曲线(线性加速、指数形加速、S形加速)来规划区域的相同位移的直线运动,箭头方向为区域运动方向,将其施加于模型,观察薄膜随增加的形貌变化,选择合适的运动规律曲线。
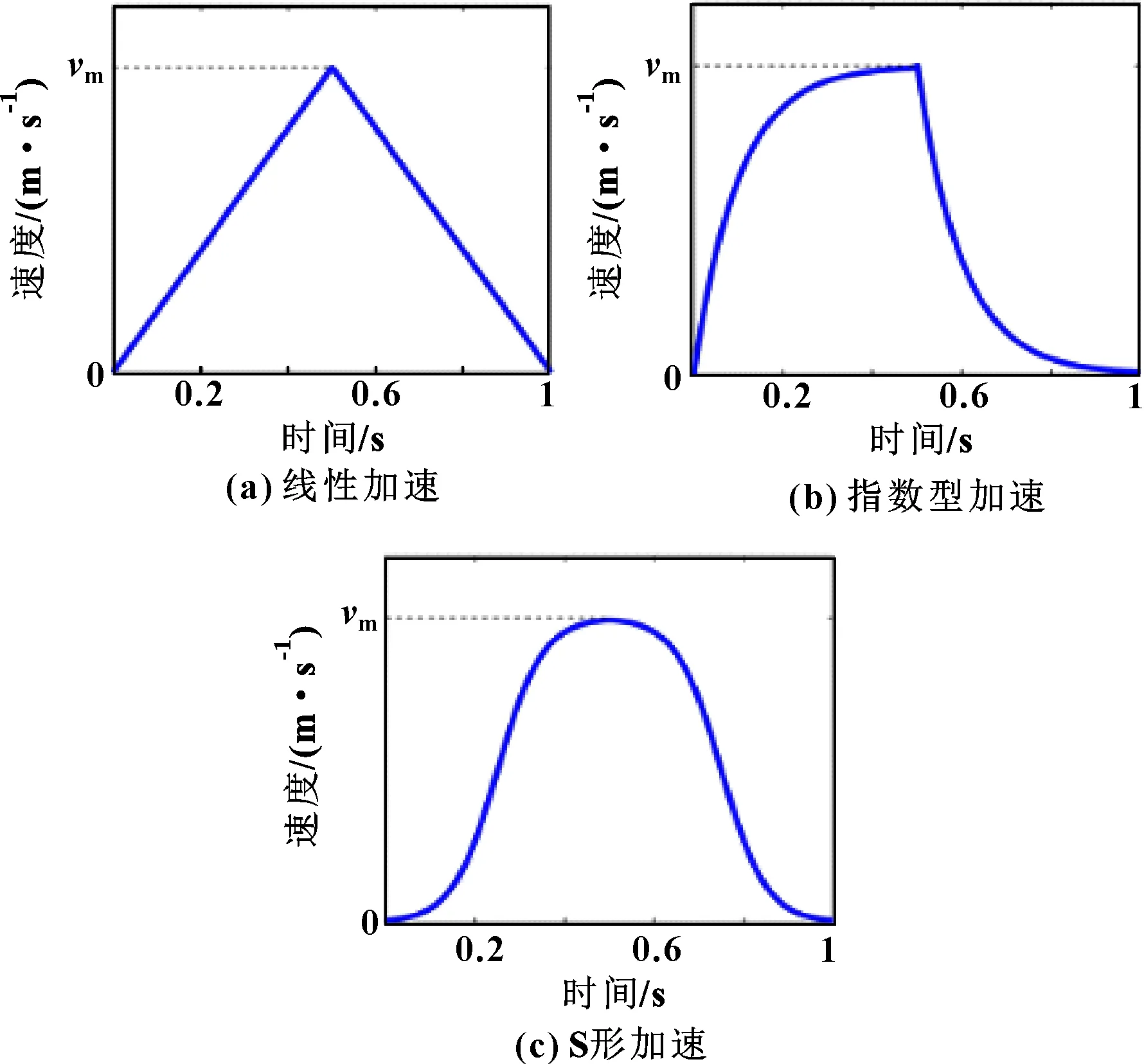
图8 3种加速曲线
将银浆薄膜在3种不同运动规律下随着增大的仿真结果导出,并计算其夹角、粗糙度,绘制成图9。

图9 不同运动规律下薄膜的变化情况
可以看到:薄膜的变化受加速度影响明显:3种加速曲线运动后的夹角和粗糙度整体都随着的增大而增大,当最大速度为[1,5] m/s时,3条曲线的加速度都较小,区别不明显,因此薄膜在三者的作用下变形相似;当为[5,9] m/s时,三者的夹角变化仍然无明显差别,但线性加速曲线下的薄膜粗糙度明显小于其他2条曲线,原因是指数形加速曲线与S形加速曲线的加速度会随着时间变化,且两者的最大加速度都高于线性加速曲线的恒定加速度,且薄膜粗糙度相比夹角更易受加速度影响;如果继续增大到9 m/s以上,在指数形加速和S形加速曲线下银浆薄膜的夹角和粗糙度急剧增大,并有部分薄膜出现断裂现象,无法继续保持薄膜状,甚至会有部分银浆飞溅出来,此时继续用这二者作为指标衡量薄膜变形已无实际意义,如图中红色×标记点;线性加速曲线下的银浆薄膜夹角和粗糙度增长相对缓慢,但也开始逐渐出现断裂的趋势。可以断定,薄膜运动时的加速度大小和加速规律对薄膜形貌有非常大的影响,而在同样的位移下,线性加速曲线加速过程中加速度始终保持恒定且小于其余2种曲线的最大加速度,使得线性加速运动对薄膜影响最小。
3 结论
在激光诱导硅片正面电极化设备运输银浆薄膜过程中,对于微米级别厚度的薄膜,运输过程的加速度越大,薄膜的变形越大,且线性加速、指数形加速、S形加速3种加速规律对它运动后的形貌均有不同程度的影响,其中线性加速运动的变形最小。旋转运动相对于直线运动,对银浆薄膜形貌影响更大,且法向变形比切向大,但中间部分整体相对均匀。为使激光诱导正面电极化设备能够成功转印,电机可以考虑采用线性加速的方式,或考虑增大玻璃涂膜面积,对中部薄膜相对均匀部分进行印刷。仿真实验证明了该设备在印刷大面积光伏硅片正面栅线时,银浆薄膜能够保持良好形貌,为后续激光诱导转移的可行性打好基础。
