基于模糊熵与CS-ELM的供输弹系统早期故障识别
2022-09-18韩慧苗许昕潘宏侠李磊磊
韩慧苗,许昕,潘宏侠,2,李磊磊
(1.中北大学机械工程学院,山西太原 030051;2.中北大学系统辨识与诊断技术研究所,山西太原 030051)
0 前言
供输弹系统是非常复杂的机电液一体化系统,作为火炮等某些高速自动武器中重要的一部分,由于它运动时猛烈撞击等现象频发,该系统工作的可靠性成为故障诊断领域专家研究的重点。若在系统故障发生之初就可知并给予维修和保养就能减少很多损失。因此,寻找一种能够提高供输弹系统早期故障诊断率的方法具有重要意义。
熵用于度量时间序列的复杂程度,在供输弹系统的故障识别应用中,付志敏通过提取近似熵和样本熵对它进行识别。样本熵虽然精度比近似熵更高,但是有无法对信号在不同尺度上的复杂程度进行充分表征等问题,然而模糊熵不仅能通过不同时间序列的子序列之间对应位置元素的最大差值表征它们之间的距离,也可表征时间序列的幅值;梁振奇通过建立基于模糊熵的路段评价模型对城市路段交通状态进行评价;丁伟等人通过提取模糊熵作为齿轮故障的特征值对各种故障状态进行分类,他们均取得了较好的效果。相比于其他的信息熵,模糊熵能较好地表征时间序列之间的差别,所以本文作者引入模糊熵特征指标表征供输弹系统的早期故障特征。
极限学习机(Extreme Learning Machine,ELM)算法是由黄广斌教授等提出的,该算法在应用中表现出很强的优势,当下已被运用到很多回归和分类问题中,但是由于隐层节点数往往为手动输入,导致预测结果的准确率较低。学者们提出许多优化算法来解决此问题,GENG等运用FAPH对ELM算法进行改进,YANG等也对ELM算法进行过改良,但是他们都未对极限学习机的模型结构进行改进,而且还存在构建模型复杂和计算量大的问题。布谷鸟搜索(Cuckoo Search,CS)算法除所需参数少之外,搜索目标的路径选择也比较优秀,整体的寻优能力强、效率高。因此,本文作者采用CS算法对极限学习机模型进行优化改进。
本文作者将模糊熵能量特征提取与CS-ELM运用于供输弹系统早期故障预示中。经试验验证,该方法能有效识别供输弹系统的早期故障,准确率达90.7%。
1 自适应TQWT滤波器算法
可调品质因子小波变换(Tunable Q-factor Wavelet Transform,TQWT)理论是由SELESNICK提出的。在TQWT中,=(,,)影响着可调品质因子小波和需要处理的时间序列特征分量的相似性匹配,其中为参数品质因子、为过完备系数、为分解的层数,对、、的选择在故障特征提取与降噪中相当重要。针对参数空间下特定的(,,),基于能量加权归一化小波熵INE(,,)的可调因子小波变换的具体过程为:
(1)对二维参数网格空间(,)进行定义:
{(,)|∈[∶∶],∈[∶∶]}
(1)
其中:{∈[∶∶]}是的取值范围和增量;{∈[∶∶]}是的取值范围和增量。
(2)对参数组合(,)选取合理的,若和确定,则的计算公式如下:

(2)
其中:是所输入的时间序列()的长度。则较为合理的分解层数=min(,)
(3)针对可调因子小波变换=(,,)构成的参数空间,对输入时间序列()进行多尺度可调因子小波变换分解:

(3)
(4)用(,,)来评估TQWT多尺度分解小波系数的稀疏性。 当可调因子小波变换的参数组合为(,,)时,通过以下3个公式计算INE(,,):
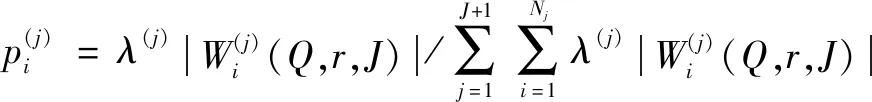
(4)

(5)
INE(,,)=(,,)max{IE(,,)}
(6)

(5)监测和整合下INE(,,)的变化情况,选择INE(,,)最小时对应的最优=(,,),构造自适应可调品质因子小波。
(6)按照图1重构各尺度下的各个子带信号,以便后续提取重构后的子带信号特征。其中,uDFT和uDFTI分别表示离散傅氏变换及其逆变换;和分别代表低通尺度变换(LPS)和高通尺度变换(HPS)的系数。
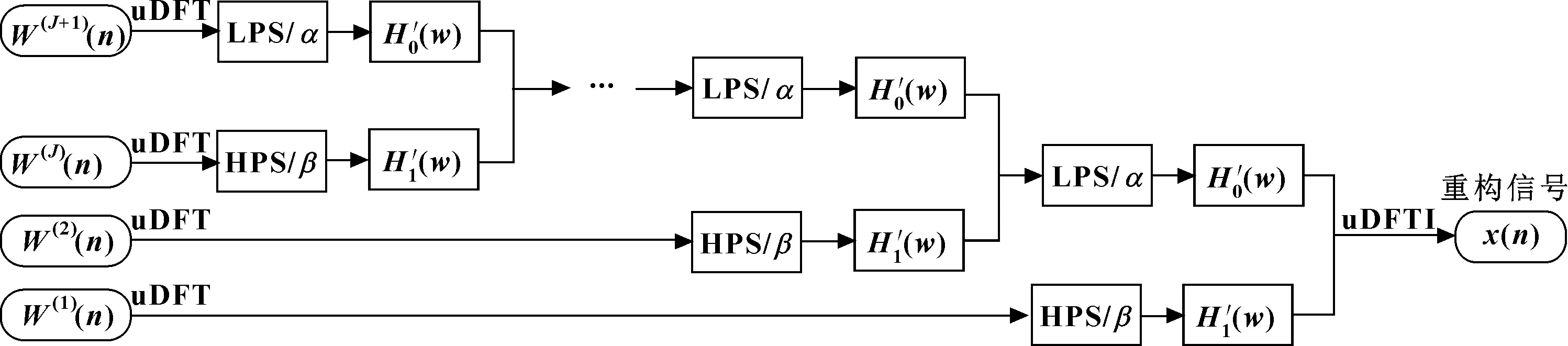
图1 可调因子小波变换的重构过程
2 模糊熵算法
模糊熵的概念是由RICHMAN基于样本熵提出的,模糊指数表征两个信号的相似度,抗噪声干扰能力很强。下面详细说明模糊熵算法的执行过程。


(7)

续 表4


[(+)-()]|},=1,2,…,-+1,∉
(8)
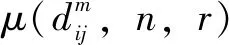
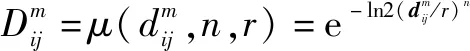
(9)

(4)计算维下的关系维度(,):

(10)
(5)增加到+1维,重复步骤(1)~(4)得到+1(,):

(11)
(6)模糊熵的定义为

(12)
式中:若为有限值时,(,,)可表示为
(,,,)=ln(,)-ln+1(,)
(13)
3 CS-ELM算法
为提高早期故障预示准确率,针对隐层节点数的确定运用布谷鸟搜索算法进行改进。以下是CS-ELM算法的详细步骤:
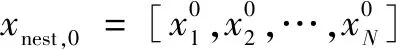

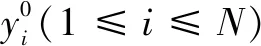
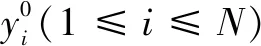
(5)为每个鸟巢中产生服从均匀分布的概率,若>,则对鸟巢的位置进行更新;
(6)若达到,停止寻优,得到和对应的,否则跳转至步骤(4);
(7)选出中最小的值,并获得其对应的鸟巢位置,经过圆整后输入到极限学习机模型中作为隐层层数,进行训练后输出对应的、、,并据此建立CS-ELM早期故障预示模型。 CS-ELM算法的具体流程如图2所示。
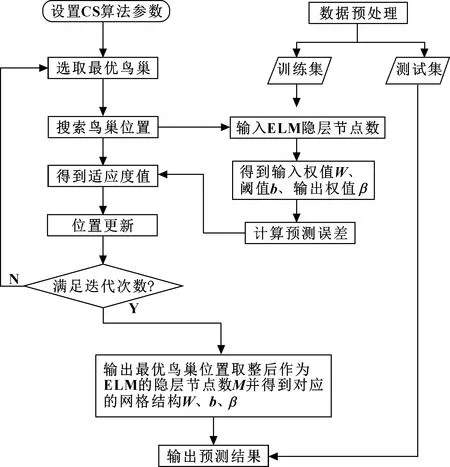
图2 CS-ELM算法的具体流程
4 试验分析与论证
4.1 试验测点布置
根据规则,测点应布置在对常见故障最敏感的位置,但受供输弹系统外形和环境的限制无法完全遵循此规则,只能选既可安装传感器又能准确反映故障状况的较合适的点。此次对某中大口径转管火炮进行测点布置,共布置振动测点6处。现场测试时的采样频率为25 600 Hz,选用32Ch-LMS信号采集装置。表1给出了测点布置位置和传感器类型,图3所示为测点布置示意。

表1 某转管火炮测点布置
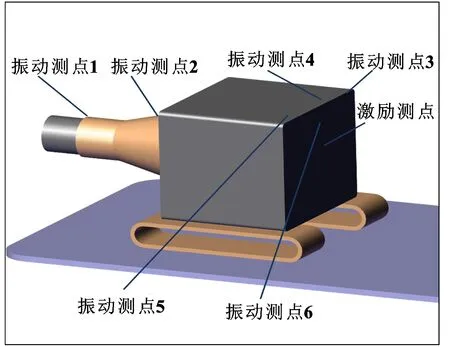
图3 测点布置示意
4.2 试验过程及记录
射击试验的装定射击速度为450发/min,即两发炮弹发射的平均时间间隔为0.133 s,以此开展该中大口径火炮供输弹系统的射击试验。具体的试验过程如下:(1)试验时,首先完成一次2连发和两次6连发的射击,射击过程中均表现良好。(2)进行一次40连发的射击试验,在此次射击过程中,虽然所有发数全部打完,但在中途第25发开始出现了射速明显降低的状况,图4所示为此次试验各发之间射击时间间隔。本文作者将此定义为早期故障工况,同时也间接说明:步骤(1)的射击工况处于早期故障的形成阶段,经专家评估后,确认其为正常工况到早期故障的过渡阶段,本文作者将它定义为早期故障的恶化工况。(3)在40连发射击试验之后,现场工作人员对供输弹系统进行了检修与维护,随即开展了60连发和80连发的射击工作,在炮弹发射时均未出现异常。
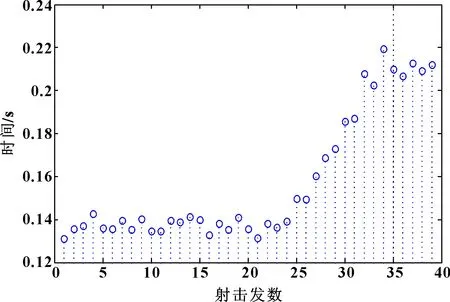
图4 40 连发射击试验时间间隔统计
4.3 基于自适应TQWT和模糊熵的信号降噪和特征提取
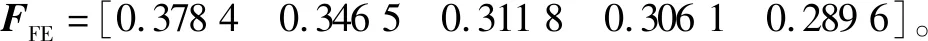

图5 5个最优特征子带
按照以上过程,对所有通过射击试验获取的振动测点的样本数据进行降噪和早期故障特征提取,并组成表示早期故障信息的特征向量集。振动测点3的部分特征向量如表2所示。在此每种工况仅列出5组数据特征向量。

表2 振动测点3的部分特征向量
4.4 基于CS-ELM的复杂供输弹系统故障诊断
针对复杂供输弹系统射击试验获取的3种工况的3个测点的194发样本数据分别进行分析处理,并提取表征系统早期故障状况的模糊熵特征。每种工况随机选取1/3的特征向量组成训练样本,共65个(正常工况47个、恶化中工况5个、早期故障工况13个),输入到CS-ELM中进行训练,CS的参数设置为=0.25、=50。将剩余样本的特征向量组成测试样本129个(正常工况93个、恶化中工况9个、早期故障工况27个),输入到CS-ELM中进行早期故障的预示。经过CS-ELM进行早期故障识别后,表3所示为射击试验振动测点3的部分样本的早期故障预示结果;同时,经ELM识别的结果如表4所示,表5所示为两种诊断结果的对比。可以发现,经CS-ELM诊断识别的准确率达到90.7%;而用ELM的综合准确率为86.82%,证明了CS-ELM方法的有效性。

表3 振动测点3的部分样本的早期
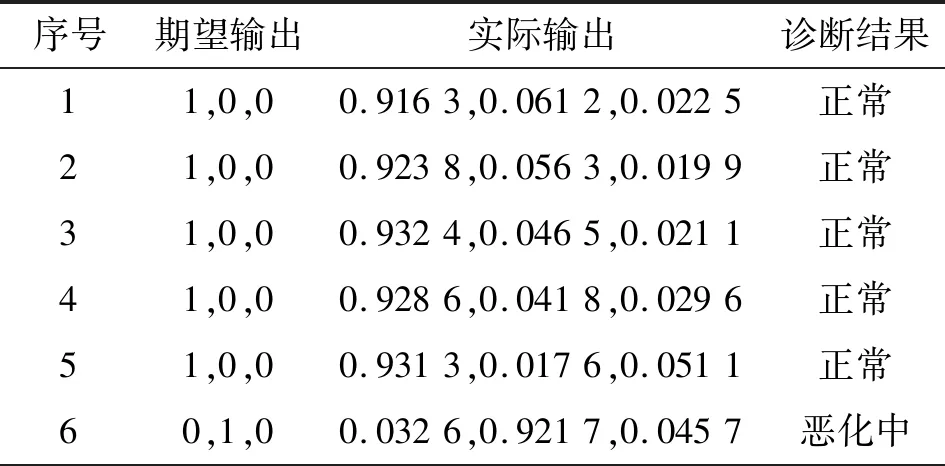
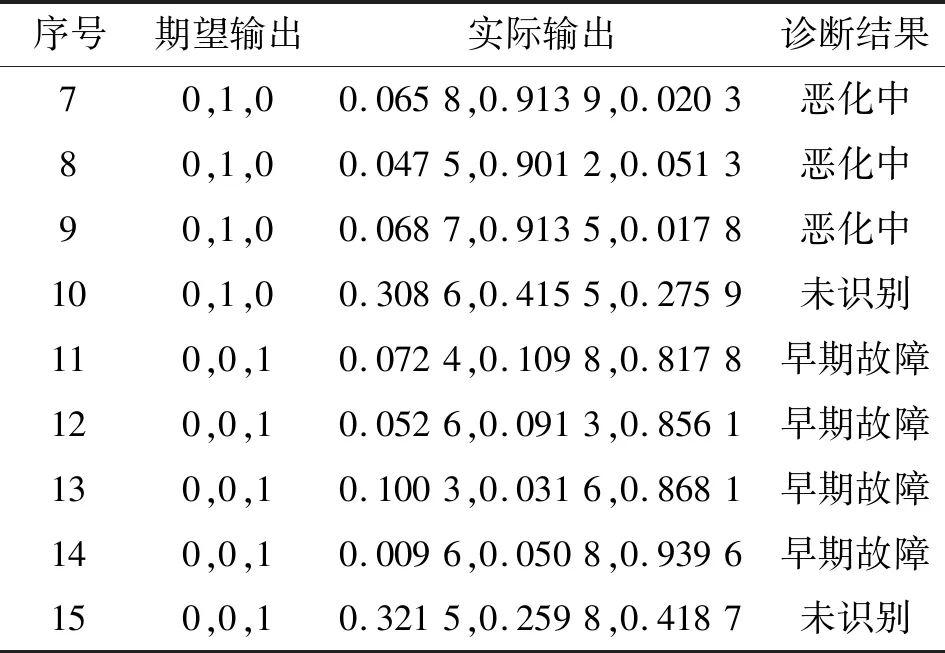
表4 振动测点3的部分样本的早期故障预示结果(ELM)
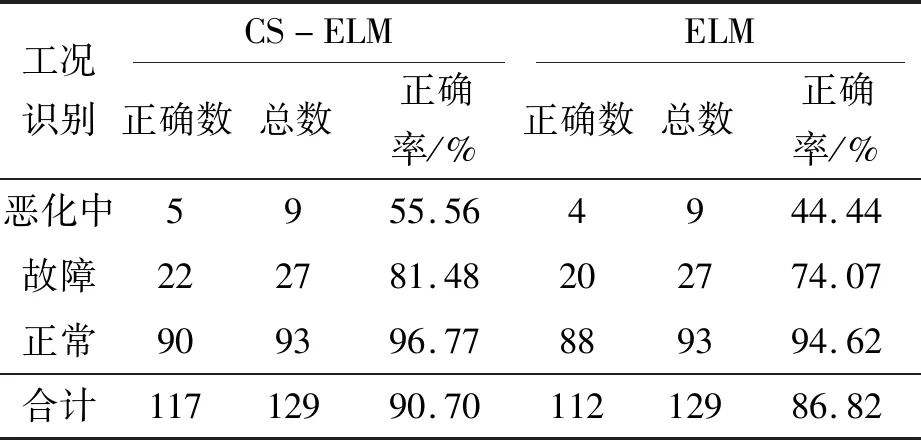
表5 诊断结果对比
5 结束语
本文作者提出一种基于模糊熵和CS-ELM的供输弹系统故障预示方法,进行基于自适应TQWT和模糊熵的信号降噪和特征提取后,针对原始极限学习机模型中存在的缺陷,采用布谷鸟搜索算法进行改进。将所提取信号的特征向量分配为训练样本和测试样本,输入到自适应优化后的极限学习机模型中进行训练和测试,并与未经优化的极限学习机训练结果进行对比。结果表明:所提的方法可在一定程度上提高供输弹系统的早期故障诊断准确率,准确率达90.7%。
