基于EEMD与GWO-MCKD的门座起重机回转支承故障诊断

2022-09-18曾耀传林云树吴晓梅

机床与液压 2022年7期

曾耀传，林云树，吴晓梅

(1.福建省特种设备检验研究院，福建福州 350008；2.福州大学机械工程及自动化学院，福建福州 350108)

0 前言

回转支承是一种特殊的大型滚动轴承，广泛应用于各种大型机械，例如港口的门座起重机。门座起重机回转支承在工作状态时各部分的受力不均以及运动状态复杂，并且由于低速重载的运行特点和大量的背景噪声，使得原本因故障产生的冲击淹没在背景噪声里，因此故障特征的提取比一般中高速轴承难。然而，在门座起重机的长期使用中，回转支承故障是难免的。如果不能及时发现这些故障并做出应对措施，将会影响门座起重机的正常运转，同时导致巨大的经济损失。

目前，少部分研究人员对回转支承故障诊断展开了研究并取得初步成果。吕学昭采用小波分解和极值域均值模态分解的复合方法对门座起重机回转支承进行故障诊断，然而小波分解中小波基与分解层数无法自适应选取。南京工业大学针对回转支承故障诊断做了较多的研究，将圆域分析、小波能量模式、双谱分析、峭度概率密度分析、加权融合算法、概率主成分分析等方法应用于实验台回转支承振动信号的降噪和特征提取，同时还将支持向量机、BP神经网络等机器学习方法应用于实验台回转支承的故障诊断和寿命预测，但因其数据来自于实验台，且故障是人为加工所形成的，与现场实际故障有一定的区别。

基于振动的信号处理方法是回转支承故障诊断最常用的方法之一。回转支承的振动信号具有非线性、非平稳特征，故无法直接从原始信号中提取到故障特征，因此需对它进行处理。然而，信号处理方法众多，选择一种合适的方法对回转支承信号处理至关重要。经验模态分解(Empirical Mode Decomposition，EMD)无需预设基函数，只根据自身时间尺度上的特征来分解信号，是一种具有很强自适应能力的信号处理方法。它的主要缺点是模态混叠问题。EEMD(Ensemble Empirical Mode Decomposition)克服了上述方法的局限性，并且有许多以往成功应用于旋转机械故障诊断的实例，因此本文作者选择EEMD作为门座起重机回转支承信号的处理方法。

回转支承的振动信号中往往伴随着巨大的环境噪声，信号经EEMD分解后的IMF分量仍然会有一定量的噪声存在，因此需要对IMF分量进行降噪处理。最大相关峭度解卷积(Maximum Correlated Kurtosis Deconvolution,MCKD)是MCDONALD等提出的适用于突出被噪声淹没的周期性冲击成分的算法，在轴承微弱故障诊断中取得了一定成果。然而，MCKD的使用需要提前设置滤波器长度和解卷积周期。需要指出的是，滤波器长度和解卷积周期在MCKD算法中并不是完全独立的，单独优化其中一个参数无法获得最佳的降噪效果。因此，需要采用合适的寻优算法进行参数组合的寻优。

灰狼优化算法(Grey Wolf Optimization,GWO)是由MIRJALILI等受到灰狼野外捕食活动的启发而开发的一种群智能优化算法，具有参数少、易收敛、易实现等优点。近年来，它受到了许多学者的关注，并成功应用在故障诊断领域中。

综上所述，本文作者将EEMD和MCKD两种方法相结合，用于门座起重机回转支承故障诊断。为实现MCKD参数的自适应选取，采用灰狼优化算法，以相关峭度为适应度函数对最佳参数组合进行全局寻优。

1 原理与故障诊断框架

1.1 EEMD原理及算法流程

EEMD方法通过在原始信号中多次加入等幅值的高斯白噪声，利用高斯白噪声频率均匀的特性，对多次EMD分解后的IMF分量进行平均，消除多次加入的高斯白噪声，同时有效抑制由极值分布不均而引起的模态混叠。EEMD分解的步骤如下：

(1)设定加入高斯白噪声的次数，即总体平均次数；

(2)向原始信号()中加入一组均匀的高斯白噪声()，产生新的信号：

()=()+()

(1)

(3)对带噪信号()进行EMD分解，得到若干个IMF和一个余项：

(2)

其中：,()为第次实验的带噪信号分解后的第个IMF；()为残余函数；

(4)重复次步骤(2)和步骤(3)，对得到的各IMF和余项取平均即为最终的IMF和余项：

(3)

(4)

其中:()为EEMD分解后的第个IMF；()为EEMD分解后的余项。

1.2 MCKD原理及算法流程

假设回转支承发生故障时产生的周期性信号为(),传递路径衰减响应为(),采集信号时掺杂的环境噪声为()，则实测信号()为

()=()×()+()

(5)

MCKD算法的实质是找寻最优滤波器，使得从实测信号()中尽可能地恢复周期性信号()。该算法将相关峭度最大为指标，将淹没在环境噪声中的周期性信号凸显出来。相关峭度的计算公式为

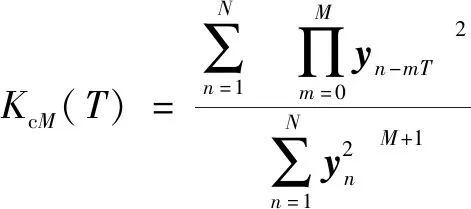
(6)

其中：为冲击信号的周期；为移位数，取值范围一般为1～7，如果大于7，精度会降低，文中选择参数为5。

若要相关峭度最大，则等价于：

(7)

其中:为滤波器长度。

最终经计算推导可得出为

(8)

其中:

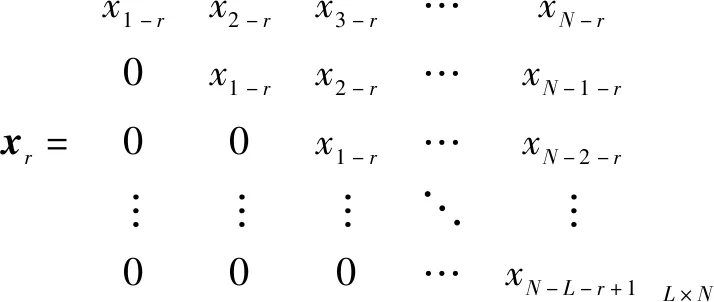
=0,, 2, …,

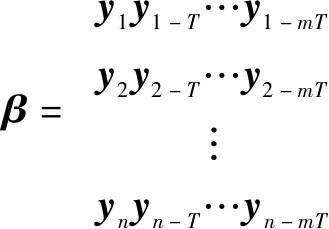
MCKD算法的流程如图1所示。

图1 MCKD流程

1.3 GWO原理

灰狼是群居生活动物，并严格遵守着金字塔等级关系。处于最顶层的头狼为α狼，负责对食物获取和栖息位置作出决策，具有领导地位；第2层为β狼，服从于α狼，同时也是α狼去世后的最佳候选者；第3层为δ狼，服从于α、β狼；最后一层为ω狼，是整个狼群的基础，同时也需要服从前3个层次的狼。灰狼捕猎主要分为3个阶段：追踪、包围、攻击。

灰狼优化算法的数学模型表示如下：

=·()-()

(9)

(+1)=()-·

(10)

其中:为狼群与猎物之间的距离；为当前迭代次数；为猎物的位置；为狼群的位置;、为协同系数，=2·-、=2，式中,∈[0,1]，在整个迭代过程中由2降到0。

灰狼搜寻猎物主要按α、β、δ狼的指引来完成。因此，在迭代的过程中，保留当前最优的3只灰狼作为α、β、δ狼，再根据它们的位置来更新狼群的位置，该过程可表示为

(11)

(12)

其中:、、分别为α、β、δ狼和猎物之间的距离；、、分别为α、β、δ狼的位置向量。

1.4 诊断方法流程框架

采用EEMD与GWO-MCKD相结合的方法对低速重载门座起重机回转支承故障特征进行提取，具体步骤如下：

(1)确定EEMD算法的参数。EEMD中有2个需要人为设定的参数：高斯白噪声的标准差和添加噪声的次数。标准差根据信号中噪声大小而定，一般为0.01～0.4，文中选择0.2；添加噪声次数通常取50或100，文中选择50；

(2)对原始振动信号进行EEMD分解，选择峭度最大的IMF作为最优分量；

(3)使用GWO算法，以相关峭度为适应度函数在最优分量上进行MCKD参数寻优。滤波器长度的寻优范围设置为[100,700]，解卷积周期=/，其中：为采样频率，为故障特征频率。因故障特征频率未知，本文作者根据回转支承参数计算理论故障特征频率，将其最大值与最小值代入公式，得到解卷积周期的范围。此外，因理论故障特征频率与实际故障特征频率存在误差，应适当将计算得到的范围扩大；

(4)将GWO寻优得到的最佳参数组合代入MCKD，以此对最优分量进行分析，并做出包络谱；

(5)将包络谱中发现的故障特征频率与理论故障特征频率进行对比分析，得出诊断结果。

整个诊断方法的流程如图2所示。

图2 EEMD与GWO-MCKD方法流程

2 回转支承平台与信号采集

文中所分析数据采集于某港口门座起重机中的回转支承，型号为132.50.4000。该回转支承结构为三排滚柱式，工作方式为外圈固定、内圈旋转。此次数据采集选取加速度传感器。由于传感器的布置直接影响采集数据的质量，故先对传感器放置的位置进行分析。为尽量减小噪声的干扰以及提高信号传递的质量，将加速度传感器放置在门座起重机的背风侧且靠近回转支承的位置。此外，回转支承主要受到轴向力、径向力和倾覆力矩的作用，应在轴向和径向均布置传感器。传感器的具体布置方式如图3所示。

图3 传感器布置

根据现场实际工作环境，选择载荷及速度较为稳定的条件下进行数据采集。采集时回转支承的转速为1.22 r/min，采样频率为400 Hz。同时为了避免遗漏故障信息，每次采样时间均大于回转支承旋转一周的时间。

3 信号分析与结果

3.1 理论故障特征频率计算

三排滚柱式回转支承可以简化为普通的三排滚动轴承。因此，其理论故障特征频率计算公式可使用滚动轴承的计算公式。具体如下：

(13)

(14)

(15)

其中：、、分别为理论内圈故障特征频率、理论外圈故障特征频率、理论滚动体故障特征频率；为回转支承中径；为滚动体直径；为滚动体数目；为接触角；为转频。

依据公式(13)—(15)可计算出回转支承理论故障特征频率如表1所示。

表1 理论故障特征频率单位:Hz

3.2 现场信号分析与对比

为避免故障信息的遗落，选择回转支承旋转两周(98 s)的数据进行分析。图4所示为此数据的时域图和频谱图。从时域图中可观察到明显的冲击成分，从频谱图中可以观察到许多突出频率，但无法从中直接辨别故障的特征频率。因此，需对原始信号进行信号处理再进一步分析。

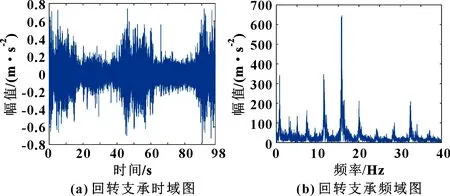
图4 回转支承时域图与频域图

依据第1.4节所提方法流程对现场信号进行分析。首先，使用EEMD算法对原始信号进行分解，得到14个IMF，计算每个IMF的峭度值如图5所示。可以看出：IMF2的峭度值最大，则选择它作为分析的最优分量；其次，根据解卷积周期公式，从表1中选取最大、最小理论故障特征频率代入，可得解卷积周期的理论寻优范围为(96,492)，将范围适当扩大为(90,500)。MCKD的参数寻优过程如图6所示。可以看出：该算法在进行到第7代的时候，相关峭度达到最大，此时对应的最佳和组合为[689,97]；最后，设定MCKD中的滤波器长度=689、解卷积周期=97，得到最优分量经MCKD处理后的包络谱如图7所示。可以观察到：包络谱中存在4.2 Hz的故障特征频率及其倍频；与表1中的理论故障特征频率对比，发现它与中排回转支承理论内圈故障特征频率4.124 Hz最为接近。因回转支承的制造安装误差与使用时的磨损和相对滑动，特征频率会存在一定的误差。因此，可以判定回转支承中排内圈发生了较为严重的损伤。整个方法的过程与结果表明故障特征频率被准确地提取，从而也验证了所提方法的有效性。

图5 各IMF峭度

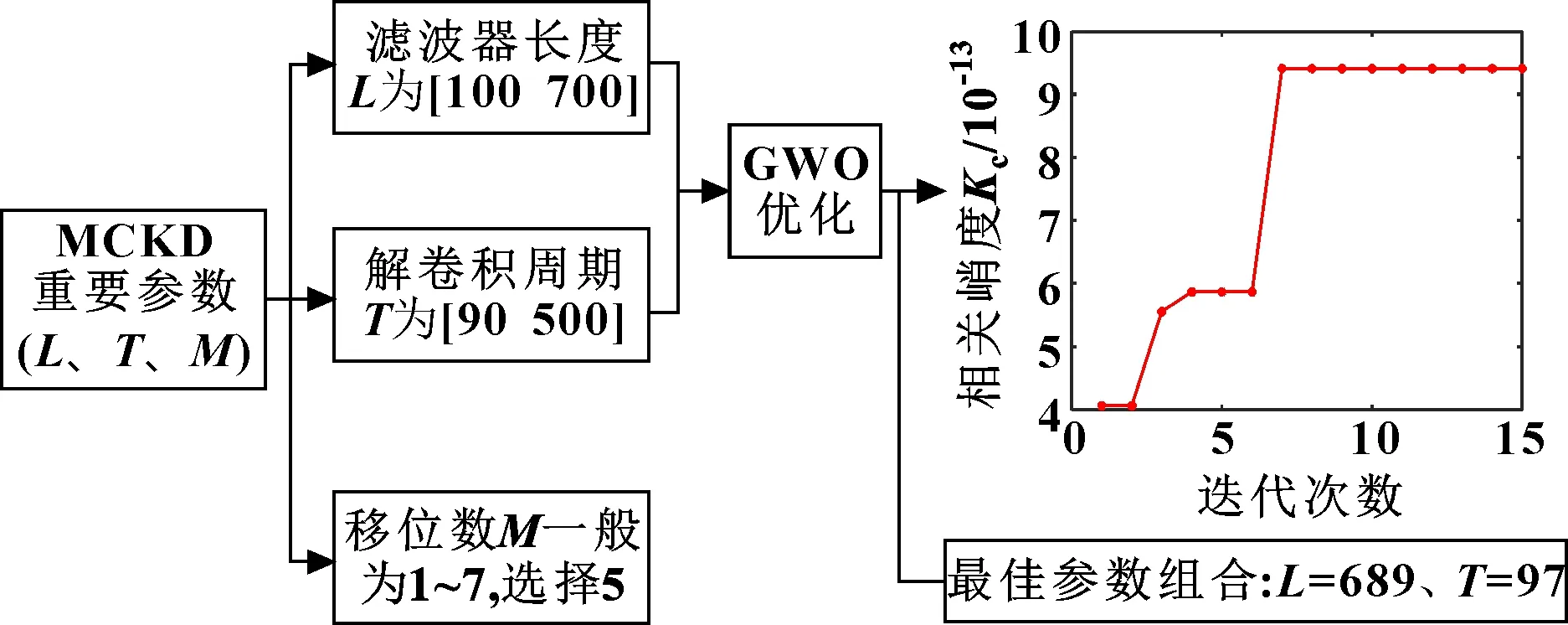
图6 MCKD参数寻优

图7 最优分量经GWO-MCKD 图8 EEMD峭度最

为证明所提方法结合MCKD算法的必要性，将EEMD分解后的峭度最优分量直接做包络谱分析进行对比。EEMD最优分量的包络谱如图8所示。可以发现存在4.2 Hz的故障特征频率，其倍频成分不够突出且伴随着许多杂频。与所提方法对比，仅用EEMD算法结合包络谱未能充分提取故障频率倍频。

为进一步证明所提方法的优越性，使用最小熵解卷积算法(MED)对峭度最优分量进行分析对比。MED算法主要受滤波器长度的影响，为使对比结果更具说服力，将MED的滤波器长度设为与MCKD的滤波器长度一致，即=689。采用MED算法对峭度最优分量进行处理后得到的包络谱如图9所示。可以看出：有较为突出的4.2 Hz的故障特征频率及其二倍频、三倍频，但未发现更高倍频且伴随着许多杂频。结果表明：所提方法在门座起重机回转支承故障特征提取上拥有更好的性能。

图9 最优分量经MED 图10 最优分量经PSO-MCKD

为证明GWO参数寻优的优越性，使用粒子群算法(PSO)对峭度最优分量进行MCKD参数寻优。PSO寻找的最佳参数组合[,]为[100,90]，在此参数下的MCKD降噪后的包络谱如图10所示。从图中仅可以观测出4.2 Hz的故障频率，无明显倍频成分，表明故障特征未被充分提取；与PSO-MCKD相比，GWO优化MCKD的结果更为可靠。