基于正交试验的双圆弧齿轮约束模态模型研究

杨树峰，禹文涛，王东飞，王峰，刘世军

(1.郑州机械研究所有限公司，河南郑州 450052；2.中原工学院机电学院，河南郑州 450007)

0 前言

齿轮旋转啮合过程中会引起齿轮系统的振动，若齿轮的固有频率与啮合频率重叠或相近，会产生共振现象。共振可在齿根产生较大的动应力，加速齿轮的疲劳断裂，尤其在高速工况下，共振失效已成为齿轮主要的失效形式。因此，在设计和试制中要提前掌握其固有频率和振型，力求齿轮的固有频率避开啮合振动频率。模态分析是研究产品结构动力特性的一种方法，在机械、土木等领域广泛应用，旨在提取产品结构的固有属性，包括固有频率、阻尼比和振型，认知系统结构参数、几何参数与固有频率、振型的关系，为结构设计、振动故障诊断和结构优化提供参考。

国内外学者对齿轮传动系统固有特性进行了大量的研究。WANG建立了行星齿轮系统的动力学模型，采用模态分析方法计算固有频率对啮合刚度的灵敏度，利用耦合因子判断过渡的发生，采用多尺度方法分析啮合刚度变化引起的参数失稳，得到了模态特征值灵敏度、模态转移准则和符合度变化不稳定性的变化规律。LIN和 PARKER研究了不同行星轮个数的单级行星轮系的模态振动问题，详细分析了多种状态下的固有频率和振动模式，分析了系统固有特性对几何参数、啮合刚度、转速等因素的灵敏度。宿博康等建立了汇流行星排齿轮系统的动力学仿真计算模型和时、频域测试试验台，进行固有特性研究，确定了系统共振频率范围，得出行星排齿轮系统的固有频率随着啮合刚度的增加而发生不同的变化，转速增加、振幅增大。莫帅等人应用集中参数法建立了面齿轮-行星传动串联系统的平移-扭转耦合动力学模型，求解了系统的固有频率，研究了啮合刚度、支撑刚度、扭转刚度和构件质量对固有频率的影响。张小萍等利用有限元分析法对双典型法向圆弧齿轮进行模态分析，计算了不同齿数、模数、传动比情况下的固有频率，得出小齿轮的固有频率对模数和齿数呈现较大的起伏变化，大齿轮则较为平缓。张兰对渐开线直齿轮和双圆弧齿轮进行了约束状态下的模态分析，得出双圆弧齿轮固有频率大于直齿轮，轴的有效惯量对振型的影响最大，且直齿轮的有效惯量明显大于斜齿轮。

上述研究成果分别采用有限元法和试验模态法研究了几何参数、系统刚度对直齿轮、斜齿轮、行星轮系等齿轮传动系统固有特性的影响，但相关研究大多定性地分析几何因素的变化对固有频率的影响，缺乏定量地研究影响固有频率的因素的主次顺序，鲜有对双圆弧齿轮固有频率数值简化计算模型进行求解。因此，如何能够定量确定几何因素对固有频率的影响，归纳出双圆弧齿轮固有频率简化计算模型，是一个亟待解决的实际问题。本文作者采用统计学理论，基于有限元法模态分析理论，建立以双圆弧齿轮几何参数(模数、齿数、螺旋角、齿宽)为自变量，约束模态固有频率为应变量的四因素四水平的正交试验模型，定量分析几何参数对固有频率的影响，并根据值进行影响度排序，利用中心化一次非线性回归模型，建立双圆弧齿轮约束模态低阶频率回归方程。

1 双圆弧齿轮模态分析

1.1 模态分析相关理论

将多自由度的模态分析求解简化为微小位移的自由度线性弹性系统，忽略非线性因素，如阻尼、非线性接类型。其无阻尼自由振动方程为

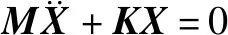
(1)

式中:为广义坐标列阵,=[,,…,];、分别为系统的质量矩阵和刚度矩阵，均为对称矩阵。对于线性系统，其振动方式为简谐振动

=cos()

(2)

式中:为第阶振型的特征向量;为第阶的固有频率。将式(2)代入式(1)，可得矩阵方程

(3)

方程(3)有非零解的条件是其系数矩阵的行列式为零，即:

(4)

可求得个特征值，其中为各阶的固有频率，可求得对应的特征向量，即为模态振型。

1.2 双圆弧齿轮约束模态分析

按照GB/T 12759—1991标准齿形几何关系，依据齿轮参数(=51、=4 mm、=24°、=20.263°、=60 mm)，采用Croe软件建立双圆弧齿轮参数化实体模型。将几何模型导入Workbench软件中，定义模型材料为软件默认的结构钢，由于低阶频率表现为网格无关性，即网格类型和疏密对模态分析中低阶频率和振型结果影响不大，故对模型采用四面体大尺寸快速划分网格。根据齿轮运动副的实际运动约束状态，对齿轮内孔面的径向、轴向、法向的位移和转动分量进行全约束设置。不考虑外在激励的影响，提取前6阶模态。双圆弧齿轮前6阶模态特性如表1所示，前6阶模态振型如图1所示。

表1 双圆弧齿轮前6阶模态特性

图1 双圆弧齿轮前6阶约束模态振型

2 正交试验

正交试验是一种研究多因素试验的重要数理统计方法。利用正交表可快速找出试验因素的最佳水平组合，了解试验因素的重要程度及交互作用情况，实现试验因素的合理、有效安排，最大限度地减少试验误差，具有高效、快速、经济的显著特点，广泛应用于化工和国民生产的各个领域。

2.1 试验设计

试验采用4因素4水平的正交试验设计，采用Workbench中的Model选项求解双圆弧齿轮的约束模态。分别选择双圆弧齿轮的齿数、模数、螺旋角、齿宽作为研究对象，每个自变量分别由4个水平组成，试验顺序采用拉丁方顺序进行，避免产生顺序效应。根据上述的双圆弧齿轮模态振型及频率，可知第2阶与第3阶、第5阶与第6阶振型和频率相差较小，固有频率越低，越容易被外界激励，故在模态分析中应对齿轮低阶固有频率的影响因素进行分析。因此，后期对1阶固有频率进行回归分析。

在小学阶段的语文教学中，最终的教学目标，就是锻炼学生的读、写、听、说等能力，使其具有相应的基础能力，为后续的学习打下有利基础。而通过小组合作学习这一模式的引入，不仅有助于该目标的达成，也能进一步地增强学生的合作意识、集体精神、学习能力等，使其获取到更加完善、健全的发展，将学科价值全方位地展现出来。

2.2 试验方案

采用L(4)的正交试验表，其中L为正交符号，16为正交表横行数，4为因素水平数，5为正交表纵列数。将自变量的各因素安排在正交表对应的位置上，一般1个因素占1列，不同因素占不同的列。如表2所示，A代表齿数，B代表模数，C代表螺旋角，D代表齿宽，E代表空列，表中的1～4分别看作各个因素的水平数，正交表对应的每1行为1个试验方案，即各因素水平组合，空白列对试验没有影响，主要是考察试验误差。

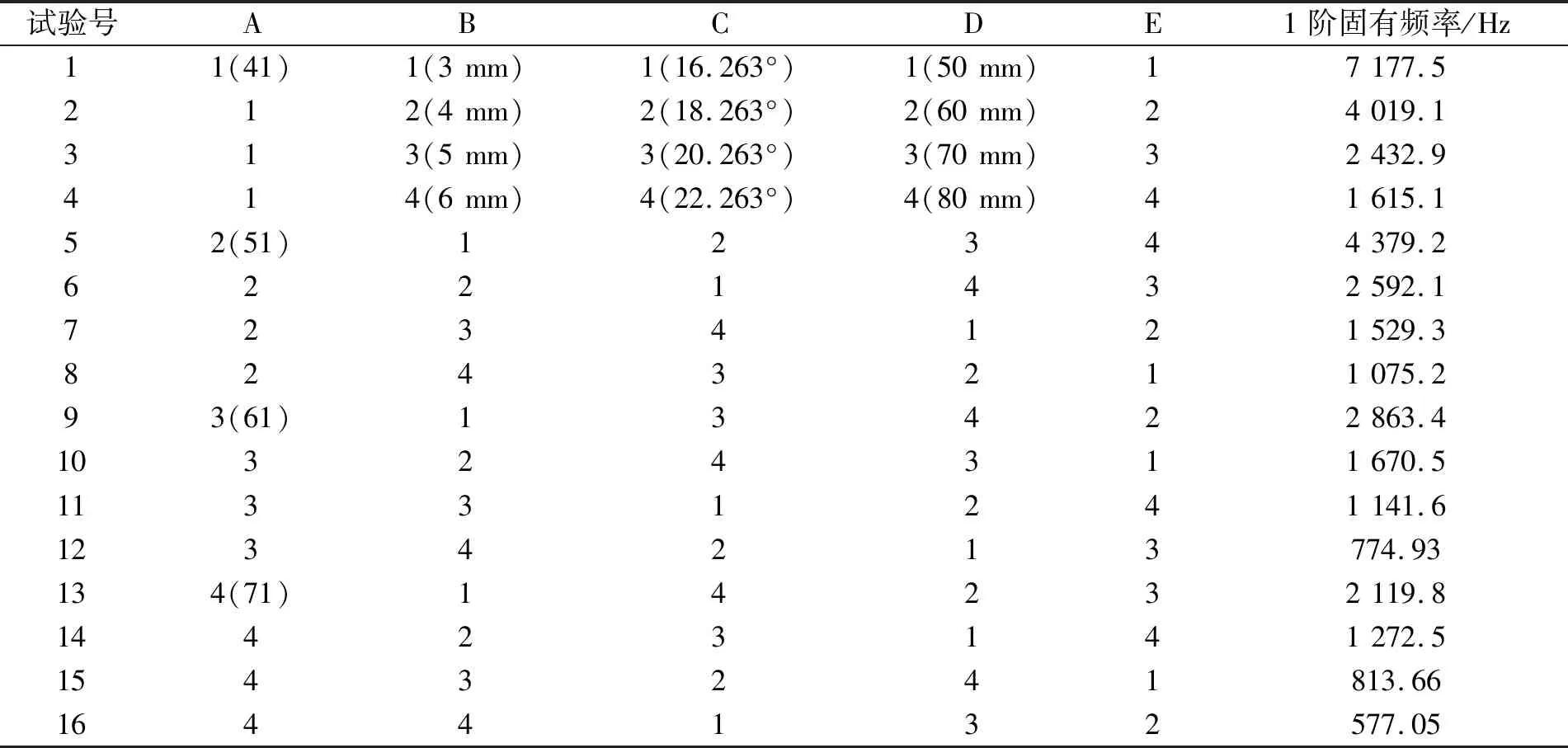
表2 约束模态正交试验方案及结果

3 结果分析

3.1 方差分析

将正交试验的自变量和应用Workbench软件求解的双圆弧约束模态的固有频率数值汇总，运用SPSS软件进行正交试验，对双圆弧齿轮约束模态的第1阶固有频率作方差分析，结果如表3所示。根据表中值，可确定影响双圆弧齿轮约束模态固有频率的变量的重要性由大到小依次为B、A、C、D，即模数对约束模态固有频率的影响最大，其次是齿数，然后是螺旋角和齿宽。因素B的显著性概率=0.017，因素A的显著性概率=0.029，均小于0.05，因素C、D的显著性概率均大于0.05，表明因素A、因素B对试验结果有显著影响，因素C和D对试验结果影响不显著。

表3 1阶频率正交试验方差分析

不同齿轮参数组合的1阶固有频率趋势如图2所示。可知：固有频率在齿数为41时最高，齿数为71时最低，随着齿数的增加，固有频率下降的趋势变缓；随着模数的增加，固有频率呈下降趋势；螺旋角从16.263°增至22.263°时，固有频率整体呈下降趋势，但是频率变化区间小于不同齿数和模数时频率的变化区间；齿宽从50 mm增至60 mm时，固有频率下降明显，但是从60 mm增至70 mm时，固有频率不降反增，从70 mm增至80 mm时，固有频率为下降趋势。综上可知，双圆弧齿轮约束模态1阶固有频率整体上随着自变量的增加呈下降趋势。

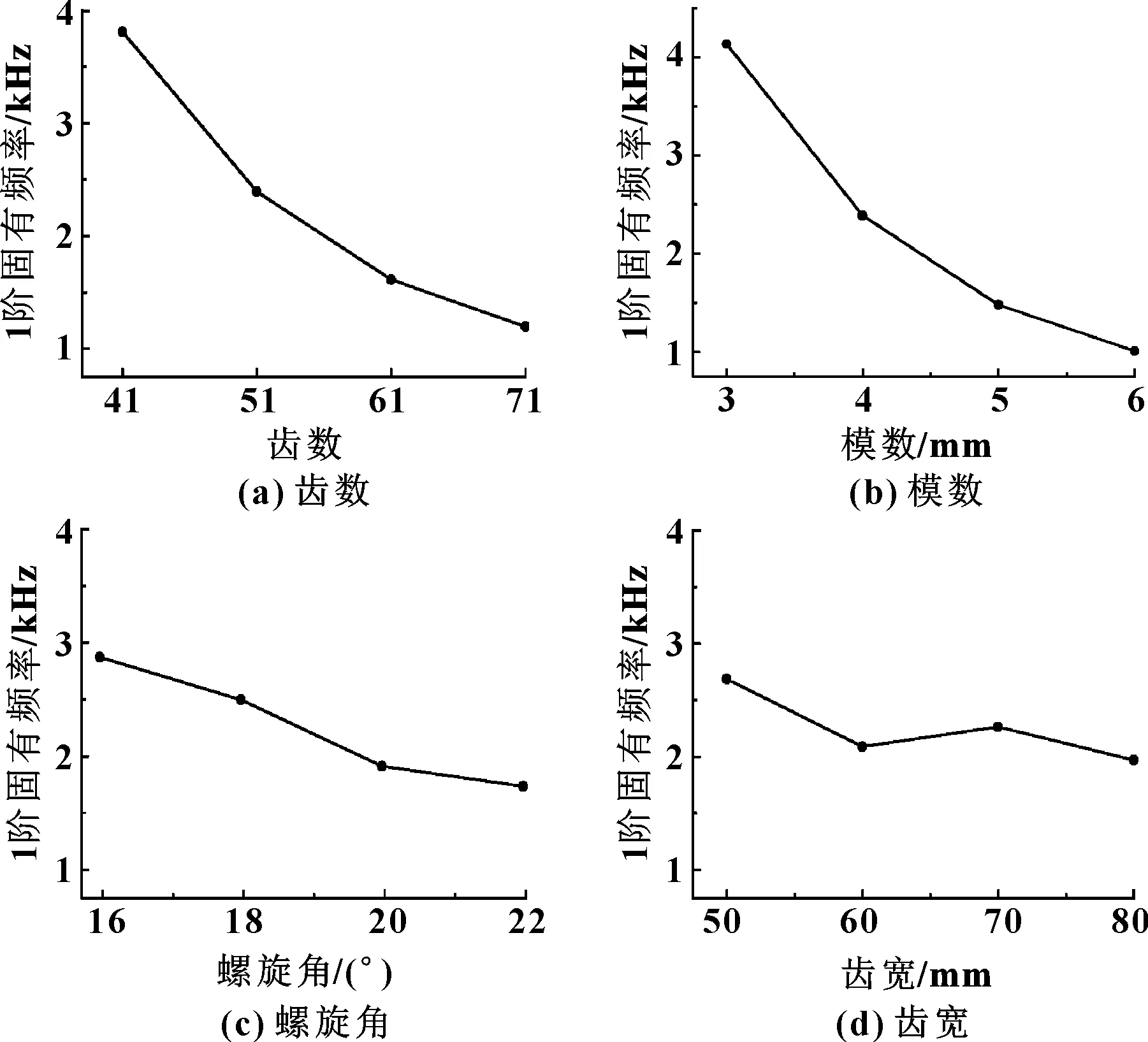
图2 不同齿轮参数时的1阶固有频率

3.2 回归分析

回归分析是一种预测性的建模技术，研究的是因变量和自变量之间的关系。此次试验涉及4个自变量，自变量单位各不相同，给回归方程的结构分析带来一定困难。对于多元线性回归，应先对数据进行中心化，以消除量纲、数量级不同的影响。在选择回归模型时，除了考虑两自变量之间的交互作用，可能还需考虑三自变量或者四自变量之间的交互作用。但是大量的实践表明，高阶的交互作用常常不存在或者很小，可以忽略。因此，采用如下原则：保证各自变量的主效应，尽量估计两两自变量之间的交互作用。由于无法直接给出自变量间交互作用的结构，故采用中心化一次非线性回归模型，其模型为

(5)

鉴于前文的研究成果，即几何参数中齿数、模数对双圆弧齿轮约束模态固有频率影响特别显著，而螺旋角、齿宽影响不显著。为获得更简洁的固有频率回归方程，建立以双圆弧齿轮齿数和模数为自变量的回归方程。

分析表3中因变量和自变量数值可知，因变量与自变量数值差较大，若直接进行回归分析，会导致回归系数以及标准误差较大、拟合度较差。分别计算1阶固有频率和齿数在原始数值、二次幂、三次幂、平方根、倒数、自然对数对应的决定系数，结果如表4所示。

表4 1阶固有频率与齿数的决定系数

决定系数用来判定回归线的拟合度，即应用最小二乘法回归方法产生的预计值与实际观测数据的拟合程度,决定系数越大表明拟合度越好。在表4中，最大的决定系数0.998由双圆弧齿轮齿数的自然对数值ln与固有频率自然对数值ln拟合，=674.495，对应的显著性检验概率为0.000，小于0.001，可知齿数的自然对数对固有频率的自然对数影响极显著。即最终回归方程因变量(约束模态1阶固有频率)的形式为ln。

同理，决定系数最大额的所有自变量参数形式如下：

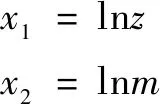
(6)

将表3中关于齿数、模数以及频率的数据分别代入式(6)和回归方程模型式(5)中，用MATLAB软件中的Regress指令进行数据中心化的多元非线性回归计算，决定系数=0998 9、=3 5115、=0000，绘制出响应曲面如图3所示，确定最终的回归方程为

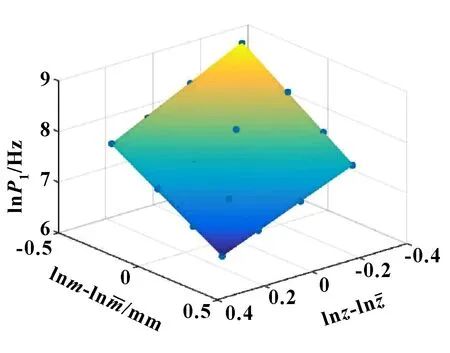
图3 响应曲面

ln=7384 5-2032 2(ln-4025 35)-

1977 7(ln-1504 08)+0555 3(ln-

4025 35)(ln-1504 08)

(7)

另取齿数=[35,60]、模数=[35，6] mm、螺旋角=20°、齿宽=45 mm，根据以上参数建立双圆弧齿轮模型。采用数值模态方法，求解出约束模态下1阶频率，对比回归方程的预测值，结果如图4所示。可知：求解值与预测值误差较小，结合回归方程和响应曲面可知，回归曲面拟合较好。

图4 仿真值与预测值对比

4 结论

为快速求解双圆弧齿轮约束模态的低阶频率，揭示齿轮主要参数对固有频率的敏感性，运用有限元法对双圆弧齿轮进行约束模态求解；在此基础上，采用正交试验法对不同齿轮参数组合进行求解及比较。对试验结果进行方差分析和多元非线性回归计算，并验证回归方程的准确性，得出以下结论：

(1)双圆弧齿轮约束模态的前6阶振型：1阶为圆周振、2阶和3阶为1阶对折振、4阶为伞形振、5阶和6阶为2阶对折振；

(2)根据方差分析结果中的显著性概率，双圆弧齿轮几何参数的齿数、模数的显著性概率均值小于0.005，得出齿数、模数对双圆弧齿轮约束模态固有频率具有显著的影响；

(3)双圆弧齿轮固有频率与几何参数(齿数、模数、螺旋角、齿宽)成反比，齿数、模数对固有频率的影响较大，螺旋角、齿宽的影响较小；

此研究将有限元计算与统计分析相结合，建立了双圆弧齿轮约束模态的首阶固有频率的计算模型。所建立的模型简单、计算便捷，为研究齿轮参数和模态固有频率之间的耦合关系提供了参考。该研究在约束模态正交试验中自变量的选择不够全面，仅对齿轮的关键参数进行了试验研究，后期试验中应进一步扩充自变量因素，优化试验方式，以更加全面地了解齿轮参数对固有频率的影响。