面向大规模航空集群组网的控制器部署方法

付皓通， 王 翔， 赵尚弘， 宋鑫康， 薛凤凤

(空军工程大学信息与导航学院，西安，710077)

随着智能航空平台的发展和多样化任务需求的涌现[1-2]，“烟囱式”独立的航空平台无法实现信息交互与任务协同功能，亟需构建一个具有高效互联互通能力，满足差异化航空业务需求，实现信息实时共享的航空集群网络[3]。

现有的航空集群网络多数基于传统的网络架构和服务模式，例如，以航空数据链和航空自组网[4]为代表的机载网络一直遵循着业务与设备紧密耦合的设计思想。虽然通过不断更新设备的软硬件能够缓解业务升级需求的压力，但这种“打补丁”的方式效率很低，使得网络协议变得臃肿，同时造成了网络管理与配置过程复杂僵化，难以适应航空集群网络成员间灵巧的交互协同。软件定义网络(software defined network, SDN)的出现打破了传统分布式网络发展的“瓶颈”[5]，其所具有的灵活性、可编程性和开放性等优点为组建航空集群网络带来了众多优势[6]。文献[7]提出了软件定义航空集群机载战术网络架构，有效地提升了网络管理效率，增强了差异化服务能力，推进了SDN与航空集群网络结合的进程。应用SDN范式构建航空集群网络，首先需要搭建控制结构，实现逻辑上的集中控制。在航空集群网络中，节点高速移动，拓扑动态变化，链路可靠性差，部署单一控制器存在性能受限和故障失效问题，可通过部署多控制器来提高网络的鲁棒性和扩展性。近年来控制器部署问题(controllers placement problem, CPP)逐渐成为了研究热点[8-9]。

目前关于控制器部署的研究主要集中在地面网络，并随着各类应用场景的出现而拓展。文献[9]首次提出控制器部署问题，指出CPP核心是控制器数量和部署位置，并分析了不同的部署方案对网络时延的影响；以此为基础，文献[10]研究了基于可靠性优化的控制器部署问题，引入贪婪算法和模拟退火算法求解，得到了可靠性更高的部署方案；文献[11]以时延和负载失衡度最小化为目标，提出基于粒子群变异函数的多目标遗传算法，提高算法收敛速度同时获得多样性更高的Pareto解。为了将地面网络控制器部署研究拓展到航空集群网络中，文献[12]基于航空集群网络场景特点，以全网平均时延、平均中断概率和控制器负载失衡度最小化为目标，提出一种基于改进蝙蝠算法的部署算法，提升了Pareto解的质量。文献[13]针对航空集群网络的拓展性，提出一种SDN航空集群网络架构，并设计一种混合优化算法来获得最佳控制器部署方案。然而现有航空集群网络控制器部署算法，所考虑的航空平台数量受限，在小规模网络场景下具有搜索速度快、寻优精度高等优点，但当网络中平台数量增多到几百架时，算法的复杂度会急剧上升，计算时间可达几小时之久，难以满足航空集群网络实时响应需求，且会对网络计算资源进行大量占用。

基于以上分析，针对大规模航空集群网络控制器部署算法所存在的计算复杂度高，实时响应能力不足问题，本文结合SDN混合式架构下的多控制器部署模型，设计一种面向大规模航空集群网络的控制器部署算法(large-scale network controller deployment algorithm, LNCDA)，所提算法分为2个阶段，首先将大规模航空集群网络进行划分，然后在子群内搜索寻优，最后得到关于Pareto前沿解的控制器部署方案。

1 系统模型

1.1 场景及控制器架构

本文基于图1(a)所示航空集群场景，该场景下存在各类有人/无人机航空平台，依据不同航空任务灵活动态组织。与地面SDN网络场景不同，在航空集群环境中，网络节点的高移动性使得传输节点与控制节点间难以稳定相连；电磁环境的复杂性使得控节点容易出现故障风险；无线链路的不可靠性使得机间通信存在较大中断概率。基于以上分析，扁平式架构难以及时掌握全局视图信息，层次式架对顶层控制器的性能提出较高要求，而混合式架构具有良好的扩展性和高效的信息共享能力，能够满足构建SDN航空集群网络的需求。因此，本文基于混合式架构[14]构建SDN航空集群网络，实现对网络的集中控制。

航空集群网络混合式架构如图1(b)所示，控制平面扩展为全局控制器平面和局部控制器平面两层。全局控制器(global controller, GC)掌握全局视图信息，负责跨区域流量转发，通常部署于生存能力、计算处理能力较强的航空平台上。局部控制器(local controller, LC)掌握局部网络视图信息，负责本区域内设备管理与流量转发，通常部署在航迹相对稳定的航空平台上。二者组成了航空集群网络的控制平面，共同维护逻辑上的集中控制。

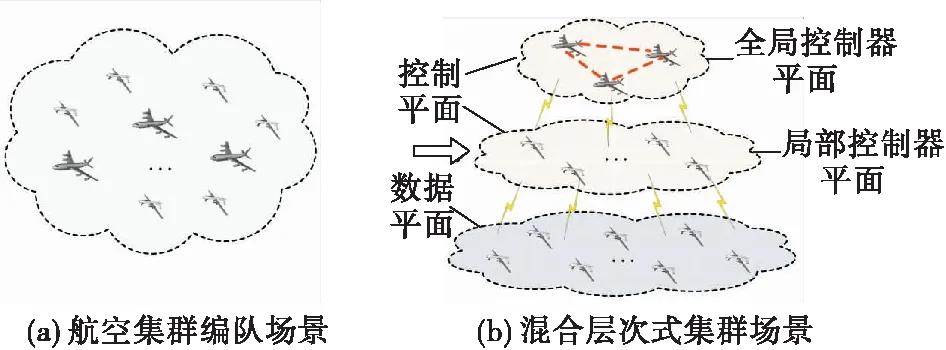
图1 航空集群场景及控制架构

1.2 控制器部署模型

文献[15]对混合式架构进行了深入研究，本文重点研究该架构下LC的部署问题。针对控制器部署作如下假设：

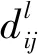
2) 网络中所有传输节点均可成为控制节点，当收到部署指令时，传输节点开启控制器功能，成为控制节点，此时认为传输节点与控制节点的时延为零。

3) 定义传输节点与LC之间的映射关系矩阵H=[xij]n×r，LC与GC之间的映射关系矩阵K=[yij]r×t。当xij=1时，表示vi映射到sj，否则为0；yij=1表示si映射到cj，否则为0。

4)网络中每个传输节点同一时间只受一个LC控制，而每个LC能控制多个传输节点；每个LC同一时间只受一个GC控制，而每个GC能控制多个LC。

5)传输节点vi的流量请求为ti，每个LC具有相同的容量，映射到同一LC上的传输节点流量请求之和不超过其容量Φ，且任意传输节点到LC的时延小于阈值τ。

6) 由于航空集群网络具有空间分布尺度大、拓扑结构动态性高的特点，采用“拓扑快照”[16]的思想来分析网络的动态运行过程。

模型的约束条件如下：

(1)

(2)

(3)

2 集群划分算法设计

航空集群网络的规模通常较大，平台数量有时可达到几百架以上，对控制平面的计算性能造成严重负担。针对上述问题，本文首先根据节点规模和相关性对集群划分，减小寻优范围，得到相关性强且分布均匀的子群。

2.1 集群划分算法的相关指标

航空集群的空间相关性很强，因此，各航空平台间的距离是衡量相关性的主要依据。同时，由于控制器的容量限制，子群规模过大将会导致控制器过载及航空平台失连现象，因此需要合理控制每个子群的平台数。为此，提出负载均衡指数B:

(4)

(5)

综合考虑平台间距离及负载均衡因素的影响，设计改进距离：

l=μD+λB

(6)

式中：D表示vi到中心节点的距离；B为vi加入到子群Gj后网络负载均衡指数；μ和λ分别为权重因子。

2.2 基于负载均衡的划分算法

文献[17]所提DPC聚类算法，得到了相关性较好的聚类结果，然而却没有考虑容量限制因素。本文提出一种基于负载均衡的划分算法(load balance based division algorithm, LBDA),以得到相关性强且均衡的划分结果。引入如下定义：

定义1 局部密度ρi。

(7)

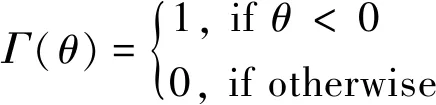
(8)

式中：ρi为节点vi在Dc半径范围中的邻近节点个数；Dc表示截断距离。

定义2 密度距离δi。

(9)

式中：δi表示节点vi到任意局部密度比它高的节点的最短距离。对于网络中局部密度最大的节点，设δmax=max(dij)。

算法首先根据网络特征参数ρi和δi得到各子群中心节点，然后将其余的节点依据l值最小原则分配到不同子群中。表1所示为LBDA算法流程。

表1 基于负载均衡划分算法

3 子群控制器部署优化

3.1 优化性能指标

航空集群网络各子群联系紧密，协同配合执行任务，子群间LC的部署位置相互影响，局部最优有时不一定能使得全网性能最优。因此本文从网络整体效能层面对控制器部署进行规划，定义了如下性能指标：

3.1.1 控制路径平均传播时延

网络中的控制路径是指GC到LC，LC到传输节点的路径。当网络状况良好时，传播时延远大于其他时延[18]，因此本文主要考虑传播时延。控制路径平均传播时延可以反映传播时延的整体情况，表示如下：

(10)

式中：α和β为权重因子，经仿真分析当α=0.8，β=0.2时更接近实际的网络传输状况。

3.1.2 控制路径平均失连概率

文献[19]已对网络可靠性进行研究，指出可靠性对于网络性能的重要意义。网络中的数据流和控制信息均由控制路径传输，控制路径的可靠性直接关系到整个网络的可靠性。

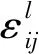
(11)

3.2 子群LC部署算法

为保证求解精确度同时降低算法复杂度，本文对文献[20]中非支配排序遗传算法II (nondominated sorting genetic algorithm II,NSGA-Ⅱ)进行改进，设计了一种具有染色体自适应交叉和变异算子的改进NSGA-Ⅱ算法(improved NSGA-Ⅱ，INSGA-Ⅱ)，动态调整交叉和变异概率，提高算法搜索能力和收敛速度。表2所示为基于INSGA-Ⅱ算法的LC部署流程。

表2 基于改进NSGA-Ⅱ算法的LC部署

表2(续)

对算法主要步骤进行说明：

1)种群个体初始化。设置种群规模pop，将种群个体分成K个均匀的子集{p1,p2,…,pK}，K为LC部署数量。

2) 非支配排序。计算每个个体P的被支配个体数np和支配个体集合Up，直到种群中所有个体的非支配等级被划分。

3) 拥挤度计算。首先任选一种目标函数fu，计算Ri+1中个体的fu值并按升序排列得到ξ，接下来计算ξ中每个个体的其他类型目标函数值。规定边界值为无穷大，即fu(ξ1)=fu(ξn)=∞。个体d的拥挤度nd的计算如下：

(12)

4)精英保留策略。将表现更优、多样性更好的个体保留进入下一代。

5)交叉、变异。采用自适应算子对所选染色体进行单点交叉和位变异操作，动态调整交叉和变异概率。

3.3 复杂度分析

INSGA-Ⅱ算法的复杂度与网络节点数n，目标函数个数m，及迭代次数I有关，其寻优复杂度表示如下：

ο(INSGA-Ⅱ)=ο(Imn2)

(13)

本文所提LNCDA算法，第1阶段将航空集群划分为子群，第2阶段在子群内部署寻优。第一阶段复杂度主要由距离值计算ο(n2)、降序排列ο(n2logn)和ρ及δ值计算ο(n2)组成，即：

ο(phase_1)=ο(n2)+ο(n2logn)+ο(n2)≈

ο(n2logn)

(14)

第2阶段在划分后的子群中进行全局寻优，复杂度为：

(15)

因此本文所提算法复杂度为：

ο(LNCDA)=ο(phase_1)+ο(phase_2)=

(16)

式中：K为待划分子群数目。

4 实验结果及分析

4.1 仿真环境及参数设置

对实验的仿真环境和参数设置作如下说明：

1)实验基于MATLAB2016a对本文所提模型和算法进行仿真实验。

2)假设所有LC节点具有相同的负载容量和处理能力；传输节点的请求为单位流量；节点的故障概率为[0,0.04]中的随机值；l和σ链路的失连概率分别为[0,0.08]和[0,0.06]之间的随机值。

3)规定当网络节点规模小于100时，GC数量为1；当节点规模大于100时，GC数量为2。GC部署的位置为网络中随机确定的节点。

4)为了体现网络拓扑的随机变化性，在给定区域内随机生成多个节点，利用Bellman-ford算法得到任意两点间的最短路径。实验中网络节点的分布范围为400 km×300 km的矩形区域，节点的通信半径为50 km。

4.2 子群划分算法性能分析

为了评价LBDA的性能，本节将LBDA与Louvain算法[21-22]和K-means算法[23-24]进行对比。

分别设置节点规模为50、100、150的航空集群，在每种节点规模下比较不同算法的负载均衡指数随子群数的变化情况。

实验结果如图2所示，Louvain、DPC和K-means算法的负载均衡指数均高于LBDA，表明LBDA的负载均衡性更优。由于Louvain、DPC和K-means算法在划分过程中只考虑节点间的相关性而没有限制子群规模，导致各子群节点数量分布不均；而LBDA综合考虑二者的影响，在保证较好相关性的同时获得更均衡的划分结果。

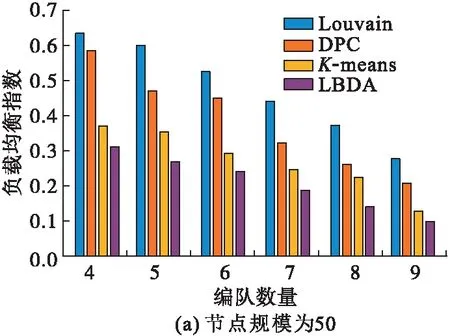
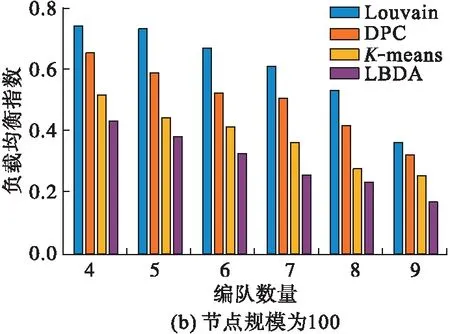
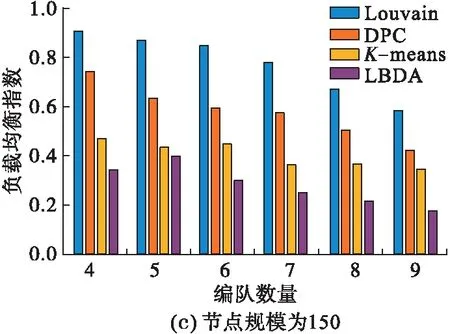
图2 不同节点规模的负载均衡指数

4.3 控制器部署算法性能分析

为评价本文所提LNCDA算法的多目标寻优能力，本节设置网络节点数为150，LC数量K=6，使用标准NSGA-Ⅱ算法, INSGA-Ⅱ算法, 穷举算法(brute force, BF)对网络进行直接寻优；而本文所提LNCDA算法将网络划分为6个子群，然后在各子群内进行寻优。几种算法的Pareto前沿对比见图3。

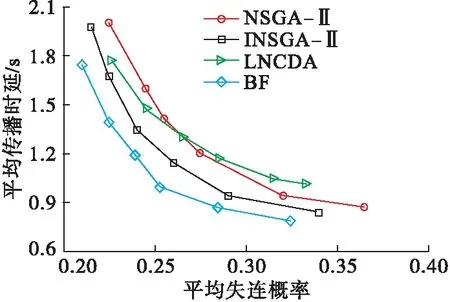
图3 Pareto前沿对比图

由图3可知控制路径平均传播时延与平均失连概率呈负相关，从而验证了CPP是一个多目标优化问题，两种性能指标之间存在一定程度的互斥关系。INSGA-Ⅱ算法性能较NSGA-Ⅱ算法有了明显提升，能获得更优的Pareto前沿，接近理论最优的BF算法。由图可知当测试算法收敛时，LNCDA算法寻优能力接近NSGA-Ⅱ算法。LNCDA算法通过集群划分，降低了网络寻优复杂度，从而使算法能够快速收敛。然而对网络划分，也限制了算法的寻优能力，位于子群中心的节点更有可能部署控制器，而子群边缘的节点在寻优中可能被跳过。因此，LNCDA算法以损失一定寻优精度的代价，获得了更快的收敛速度。

为比较不同LC数量下LNCDA算法，K-means算法，INSGA-Ⅱ算法和多目标粒子群优化算法(multiple objective particle swarm optimization, MOPSO)[25]对网络性能的优化能力，对控制路径平均传播时延、平均失连概率两种性能指标进行讨论分析，比较结果见图4。

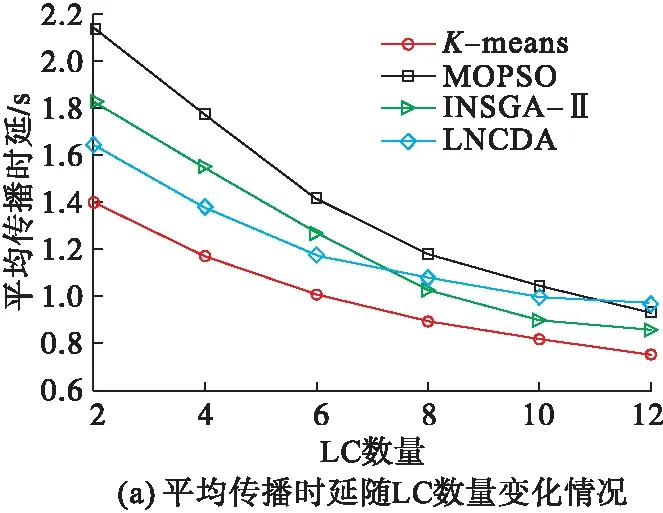
图4 算法性能指标随LC数量变化情况

由图4(a)可知，K-means算法的平均传播时延最小，因为该算法主要依据类内节点距离最短原则划分子群，而其余算法需要兼顾其他优化目标。当LC数量小于7时，LNCDA算法的时延低于MOPSO算法、INSGA-II算法，较MOPSO算法和INSGA-II算法分别降低了20.87%和12.75%。随着LC数量增加，子群数也同步增加，每个子群的规模不断减小，从而限制了LNCDA算法的寻优能力，因此当LC数量多于7时，LNCDA算法的时延会逐渐高于INSGA-II算法。

由图4(b)可知，K-means算法的平均失连概率始终高于其他算法。当LC数量小于7时，LNCDA算法的失连概率小于MOPSO算法、INSGA-Ⅱ算法，较MOPSO算法和INSGA-II算法分别降低了7.65%和5.87%；当LC数量大于7时，LNCDA算法的失连概率高于MOPSO算法和INSGA-II算法。因此，LNCDA算法在子群数量较少时表现出较好的全局优化能力。

图5为算法的平均计算时间随LC数量的变化情况。可知随着LC数量增加，K-means、MOPSO、INSGA-II算法的计算用时不断增加。而LNCDA算法的计算用时不断减少，并收敛到较低值。K-means算法，MOPSO算法和INSGA-II算法直接应用于全网寻优，搜索范围大，计算复杂度高，存在对目标重复搜索情况，易陷入局部最优解；LNCDA算法对网络进行算法划分，能够避免重复搜索的情况，具有较好的全局搜索能力。由于K-means、MOPSO和INSGA-II算法基于迭代方式寻优，当网络规模不变时，寻优变量数目增多反而使时间复杂度增加；而LNCDA算法只需要一次分域就能实现集群划分，并随着子群规模逐渐减小，寻优复杂度不断降低，因此具有更低的时间复杂度。

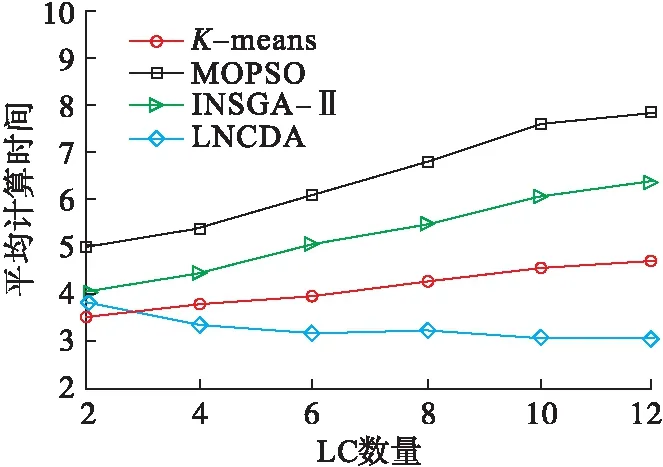
图5 平均计算时间随LC数量变化情况

5 结语

本文针对现有航空集群网络存在的业务与设备耦合紧密，网络配置与管理复杂的问题，引入软件定义网络的设计思想，搭建混合式控制架构，增强了控制平面的扩展性，实现逻辑上的集中控制；考虑到航空集群网络节点规模大，拓扑动态变化的特点，设计了一种大规模航空集群网络控制器部署优化算法，通过仿真分析证明所提算法能够有效提升网络性能，同时具有较快的收敛速度，适用于解决大规模动态场景下控制器部署问题。