预设性能控制的脆弱性问题探究
2022-09-16卜祥伟姜宝续
卜祥伟,姜宝续
(1.空军工程大学防空反导学院,西安,710051;2.空军工程大学研究生院,西安,710051)
自动控制技术使人类从繁重的体力劳动中解放出来,实现了从“手动”到“自动”的巨大跨越[1-2]。自动控制技术也是当今世界发展最快,影响最深远的技术之一。自动控制系统设计的核心是通过寻找合适的反馈控制律,使得闭环控制系统的输出定量或定性地满足“稳”“准”“快”等方面的性能指标要求。对于能控且能观的线性定常系统,总能找到合适的反馈控制律,对闭环系统的极点进行任意配置,从而对控制系统的性能指标进行任意地定量设计。然而,对于非线性系统,传统基于Lyapunov理论的反馈控制策略,通常仅能将稳态误差最终或在有限时间内调节到一个大小可调的紧集内,以实现对稳态性能的定性设计,但却无法对收敛时间、超调量等动态性能指标进行定量或定性设计[3]。
至于如何保证非线性控制系统同时具备满意的动态性能与稳态精度,IEEE Fellow、加拿大Davison教授早在1991年就进行了初步探索[4]。之后,德国学者Ilchmann等人[5]于2002年创立了漏斗控制(funnel control, FC)理论,谋求通过设计不依赖系统模型的高增益控制律来保证控制误差期望的动态性能与稳态精度。但是,由于限制条件太过苛刻,FC仅适用于极少数的一类特殊系统[5-6]。为此,在FC的基础上,希腊学者Bechlioulis等人又于2008年演化发展出了预设性能控制(prescribed performance control, PPC)理论[7]。PPC基于“性能函数设计”与“误差等价变换”的基本框架,可与现存几乎所有的控制理论相结合,从而设计出多种多样的控制律形式,将控制误差始终限定在预设的约束包络内,以便同时保证控制误差期望的动态性能与稳态精度。因此,近年来PPC已经成为控制领域的一个前沿热点方向,引起了国内外科技人员的格外关注。
1 PPC概述
PPC突破了传统控制理论无法约束控制系统动态性能的限制,实现了对控制系统动态性能的约束与调节,在保证理想控制精度的同时,兼顾超调量与调节时间等动态性能,可以保证控制系统具有较好的过渡品质。所谓预设性能是指将跟踪误差限定在一个预先设定的可调区域内,以保证跟踪误差收敛过程的动态性能与稳态性能满足预先设定的要求[7]。PPC的基本思想是设计性能函数ρ(t)∈R>0对跟踪误差e(t)的收敛轨迹进行限定,通过为ρ(t)选择特定的设计参数来保证e(t)具有满意的动态性能与稳态精度,见图1。
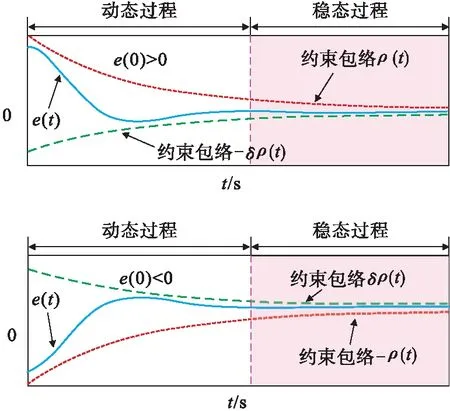
图1 PPC对误差e(t)的包络约束示意图
1.1 性能函数
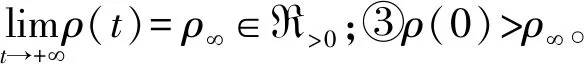
文献[7]将ρ(t)设计为ρ(t)=(ρ0-ρ∞)e-lt+ρ∞,这里,ρ0>ρ∞>0,l∈R>0为待设计参数。
如果误差初值e(0)为已知,则采用ρ(t)对e(t)进行如下包络约束:
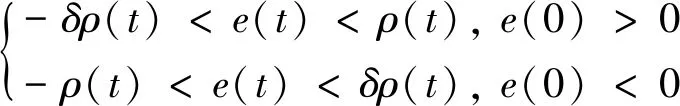
(1)
0≤δ≤1为待设计参数,由于工程实际中e(0)=0的情况很少见,文献[7]中未考虑。
注1:以0<|e(0)|<ρ(0)为例,则ρ∞表示e(t)稳态值的上界,δρ(0)表示e(t)允许的最大超调,ρ(t)的收敛速度直接影响e(t)的调节时间。因此,若能将e(t)限定在图1与式(1)所示的区域内,就可通过为ρ(t)选择合适的设计参数,来保证e(t)具有满意的动态性能与稳态精度。
1.2 误差变换
由于无法直接针对式(1)设计控制律,故引入误差变换函数S(ε(t)),将受约束系统(1)转化为如下不受约束的等价系统:
e(t)=ρ(t)S(ε(t))
(2)
式中:ε(t)∈R为转换误差,S(ε(t))的表达式为:
(3)
式(3)的逆变换为:
(4)
引理1[7]:如果转换误差ε(t)有界,则预设性能(1)可达,即对于任意e(0)满足式(1),则跟踪误差e(t)始终位于预设的约束包络(1)内。
实际的控制律是基于式(4)设计的,且控制律设计用到的是转换误差ε(t)而非跟踪误差e(t)。引理1表明,只要转换误差ε(t)有界,便能保证e(t)具有期望的动态性能与稳态精度。
2 PPC的脆弱性缺陷
近年来,PPC理论得到了快速发展,取得了一大批可喜的研究成果[8-10]。研究者们注意到Bechlioulis[7]的约束包络(1)需要根据e(0)的符号分情况进行构造,由此导致控制律也要根据e(0)的正、负情况重复进行设计,这其中可能还要涉及不同情形的控制切换问题。这种对e(0)的依赖问题严重制约了其工程实用性。为此,文献[11~12]设计了一种新型性能函数,通过设定一个充分大的性能函数初值,使PPC摆脱了对误差初值的依赖,在一定程度了增强了算法的可操作性。但是,过大的性能函数初值极易造成超调量失控,导致跟踪误差的动态性能不理想。为了克服这个缺陷,文献[13~14]利用符号函数的性质,将传统性能函数[7]改进为一种能够保证跟踪误差小超调收敛的新型约束形式;相关仿真结果表明,该方法可以保证跟踪误差小超调甚至无超调收敛。传统PPC约束包络[8-14]的收敛时间需要综合利用性能函数的所有设计参数才能定性地确定一个大致的范围,因此很难对跟踪误差的收敛时间进行定量约束。为此,文献[15~16]在充分借鉴有限时间滑模控制相关思想的基础上,设计了有限/固定时间性能函数,保证了跟踪误差在任意设定的时间内收敛到稳态。上述PPC方法仅能定性地或部分定量地保证跟踪误差期望的预设性能,鉴于此,文献[17]将小超调PPC与有限时间PPC相结合,为乘波体飞行器提出了一种定量PPC新方法,能够保证跟踪误差具有任意设定的收敛时间和稳态误差,并且超调量近似为零。除此之外,PPC在输入受限系统[18-19]与受扰系统[19-20]也有较多应用。但是,应当特别指出的是,现有PPC在处理控制执行器饱和、受扰等问题时,极易诱发控制奇异问题,表现出十分明显的脆弱性缺陷。所谓脆弱性[21-22],是指当控制执行器突发饱和或受扰时,即便采取及时有效的补偿措施,控制误差相对于饱和与扰动出现之前也会有明显的瞬时增加[19,21-22];当控制误差因增大而逐渐接近甚至越过约束包络时,就会导致控制奇异、闭环系统失稳进而控制失效、预设性能不可达,见图2。
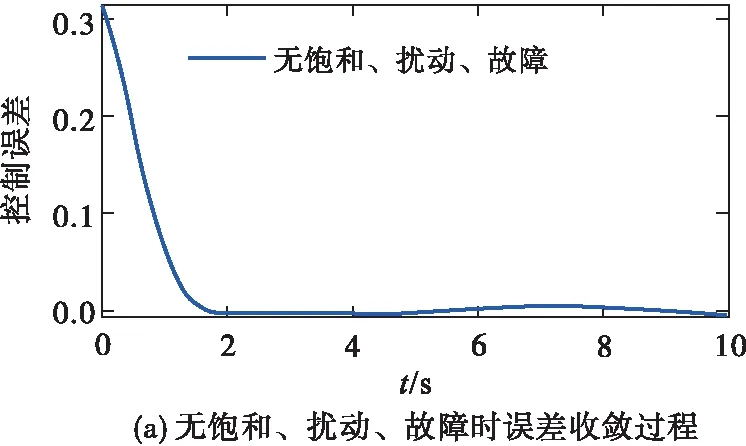
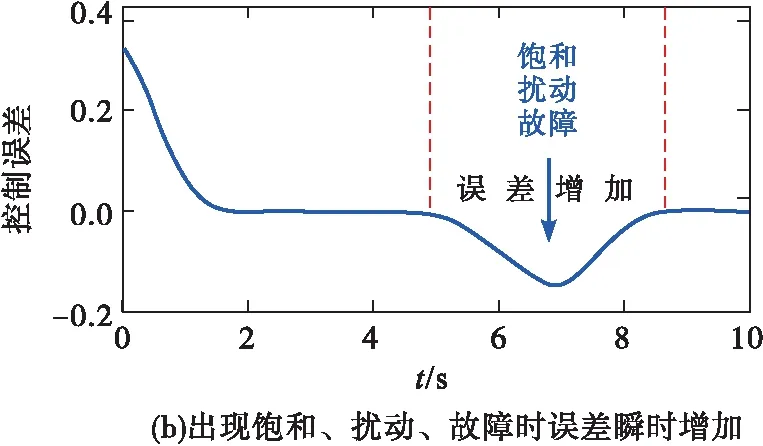
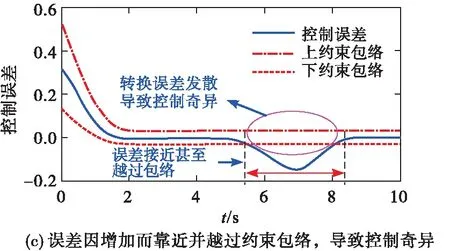
图2 PPC的脆弱性示意图
以执行器饱和为例,分析PPC的脆弱性成因。PPC以转换误差ε(t)作为反馈变量,构造反馈控制律u(ε(t)),将跟踪误差e(t)限定在式(1)所示的约束包络内。将执行器饱和定义为:
(5)

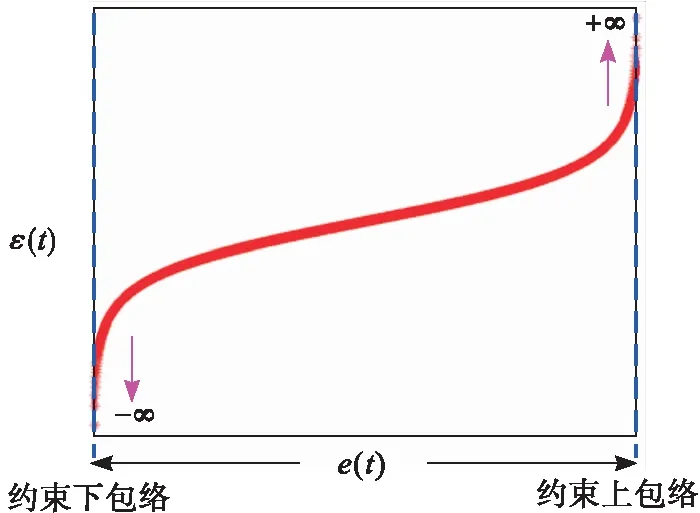
图3 e(t)靠近束包络时ε(t)变化示意图
尽管文献[18~20,23~24]的PPC方法也涉及执行器饱和与外部扰动等问题,仿真结果似乎表明方法依然有效。但是,应当清楚看到,上述方法仅考虑极短时间内的执行器饱和或较平缓的外部扰动,饱和与扰动还尚未引起足够明显的误差波动,故未能呈现出PPC的脆弱性缺陷。考虑到几乎所有的控制系统都或多或少存在执行器饱和与受扰等问题,PPC的脆弱性缺陷已经成为制约其理论发展与工程应用的技术瓶颈,是PPC走向工程实用所必须迈过的“鸿沟”。因此,探索非脆弱PPC新理论已经迫在眉睫。
3 非脆弱PPC新理论基本构想
由PPC脆弱性成因分析可见,执行器饱和、受扰等因素导致PPC控制奇异的一个关键原因是传统的预设约束包络不具备再调整能力,即预设约束包络不能实时“感知”由执行器饱和与受扰等因素引起的误差波动情况,也不能根据误差e(t)的波动情况,有针对性地自动调整预设约束包络,导致误差因接近甚至到达预设约束的上、下包络而造成控制奇异,见图2(c)。
基于以上分析,给出非脆弱PPC新理论的基本构想。所谓非脆弱PPC,是指预设约束包络能够自主感知误差波动,自动调整约束包络,从而确保控制执行器饱和、受扰等情形下预设性能始终可达的PPC新理论[9,21-22],见图4。为了达成非脆弱PPC的上述设想,需要突破误差感知、包络调整与预设可达等一系列的基础性问题。
3.1 误差感知
误差感知,是指PPC能够实时“感知”跟踪误差的波动态势,即确定跟踪误差是否存在靠近约束上包络或下包络从而导致控制奇异的风险隐患。为了确保能够准确感知误差波动情况,需要事先剖析控制执行器饱和、受扰等引起误差波动的根本原因,进而探究约束包络对误差波动的自主感知模式,从而构建的自主感知方案。
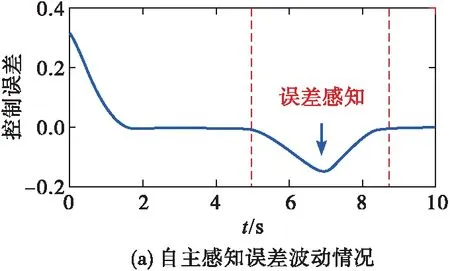
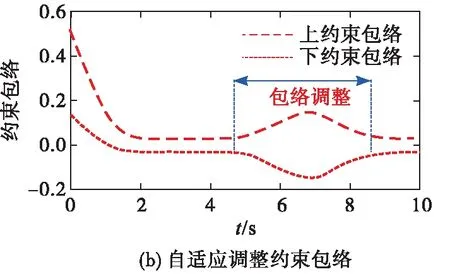
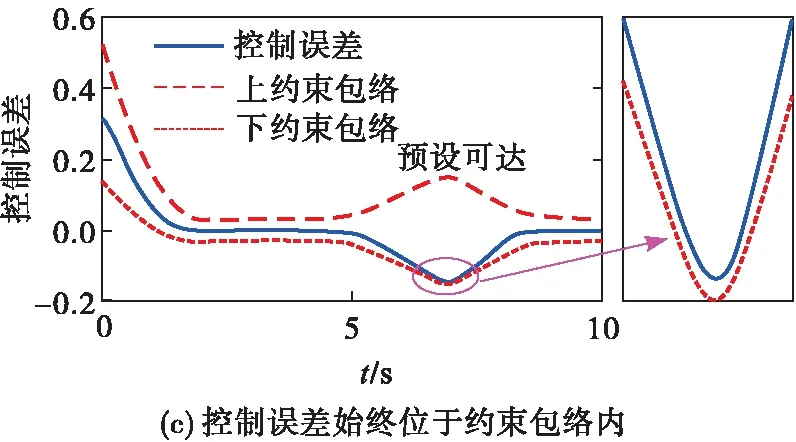
图4 非脆弱PPC关键技术构想示意图
3.2 包络调整
包络调整,是指在准确感知误差波动态势的基础上,PPC能够自动调整预设约束包络的形状(比如,当“感知”到误差增大时,可以自适应地增大约束上包络,减小约束下包络,以避免控制奇异),以保证跟踪误差始终位于约束包络内。为了达成这个目标,需要针对控制执行器饱和、受扰等导致的误差波动问题,分类研究和制定约束包络的调整方案。还要寻找导致误差波动的关键变量,探索约束包络调整项的构造方法。
3.3 预设可达
预设可达,是指在预设约束包络再调整的情形下,将跟踪误差约束在约束包络内应当满足的相关条件。为了避免饱和、扰动等导致的PPC奇异问题,需要在准确感知误差波动的基础上,设计调整项对约束包络(由性能函数构造)进行修正,修正以后的性能函数不再满足传统PPC中必须为连续单调递减的限制条件。对于这种跳出现有PPC理论框架之外的特殊情形,还需要研究采用何种补偿措施、构建何种反馈控制方案,才能保证闭环系统稳定和转换误差有界,从而保证预设性能是可达的。
4 非脆弱PPC应用案例
根据非脆弱PPC新理论的上述构想,基于笔者的前期成果[24],给出非脆弱PPC可行的技术方案。
4.1 受扰动力学系统的非脆弱PPC方案
考虑如下受扰动力学系统
(6)
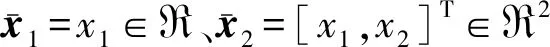
控制目标为:设计虚拟控制律x2d与实际控制律u,使得x1跟踪其参考指令x1d,x2跟踪x2d,并且跟踪误差e1=x1-x1d、e2=x2-x2d满足如下预设性能[24]:
(7)
式中:
Pl1=[sign(e1(0))-0.5]ρ1-0.3sign(e1(0));
Pr1=[sign(e1(0))+0.5]ρ1-0.3sign(e1(0));
Pl2=[sign(e2(0))-0.5]ρ2-0.15sign(e2(0));
Pr2=[sign(e2(0))+0.5]ρ2-0.15sign(e2(0));
ρ1=(2.5-0.3)exp(-0.4t)+0.3;
ρ2=(2.5-0.15)exp(-0.4t)+0.15。
转换误差为[24]:
(8)
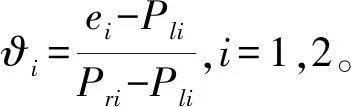
鉴于文献[24]的传统PPC不具备约束包络自调整能力,当遭遇足够强度外部扰动d1(t)、d2(t)时,极易造成控制奇异,表现出明显的脆弱性缺陷。为此,基于前文非脆弱PPC新理论的相关构想,对文献[24]方法进行改进,给出一种非脆弱PPC的可行方案。
对文献[24]的预设性能式(7)进行改进:
(9)
式中:Re,1(t)∈R≥0、Re,2(t)∈R≥0为自适应调整项,
Re,i(t)公式表示如下,式中τ1,e,i=5,τ2,e,i=1/3,i=1,2。
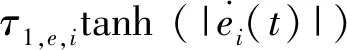
基于非脆弱预设性能(式(9)),对转换误差(式(8))修正,见式(10):
(10)
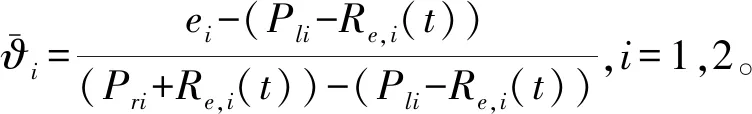
闭环控制系统的稳定性证明过程见文献[24],文中不再赘述。
4.2 输入受限动力学系统的非脆弱PPC方案
考虑如下输入受限的倒立摆系统[25]:
(11)
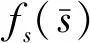
式中:mc=1 kg,m=0.1 kg,l=0.5 m,g=9.8 m/s2。
假设u∈R受到如下饱和约束:
(12)
式中:ud为u的期望值,um与uM分别为u的下界与上界。
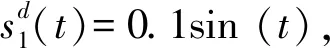
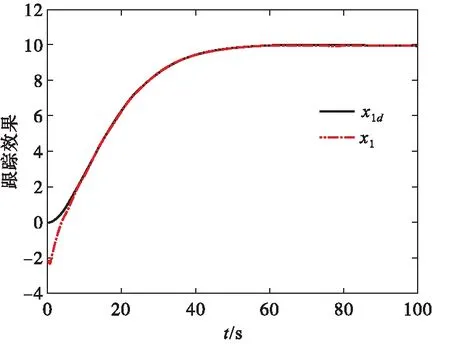
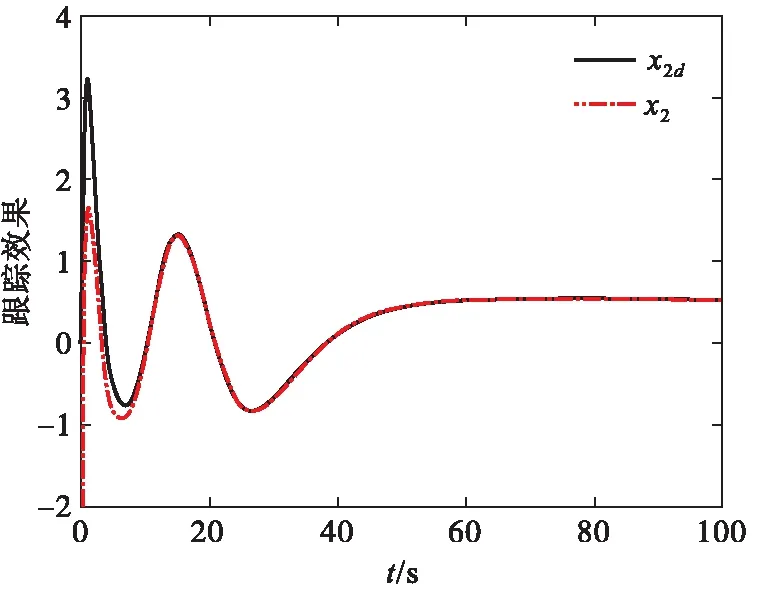
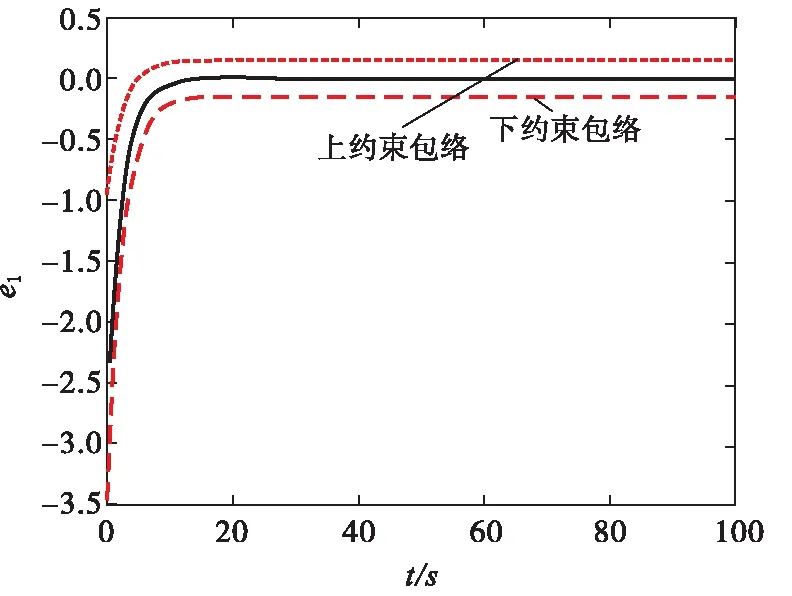
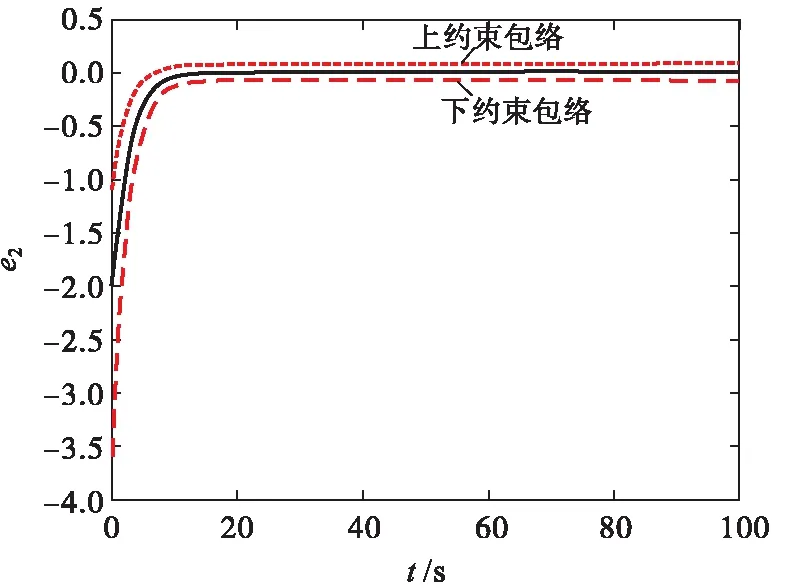
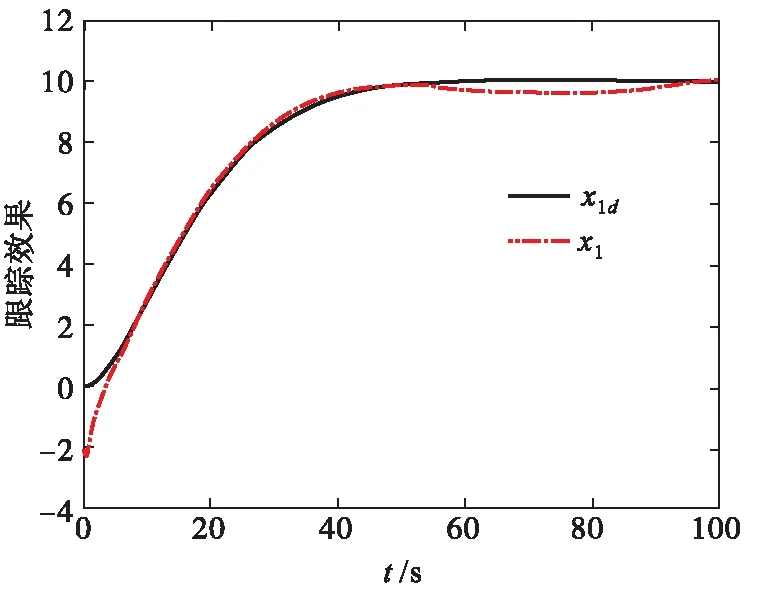
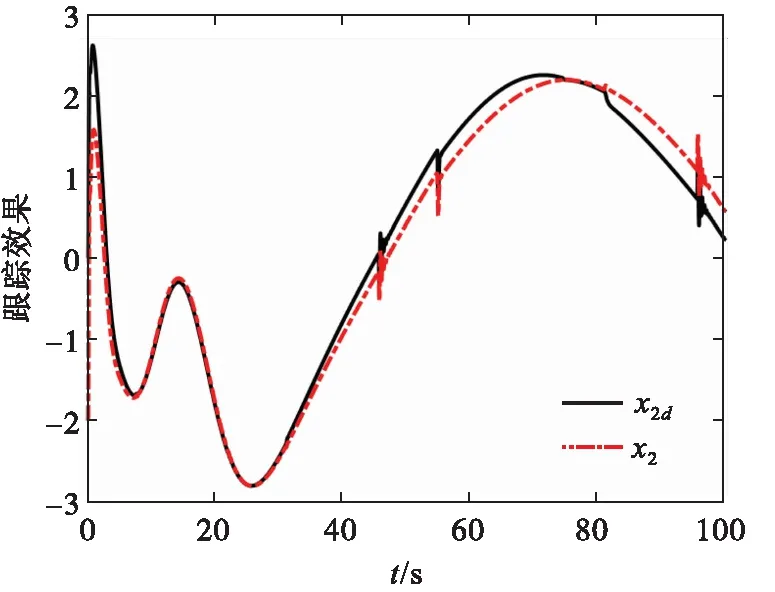
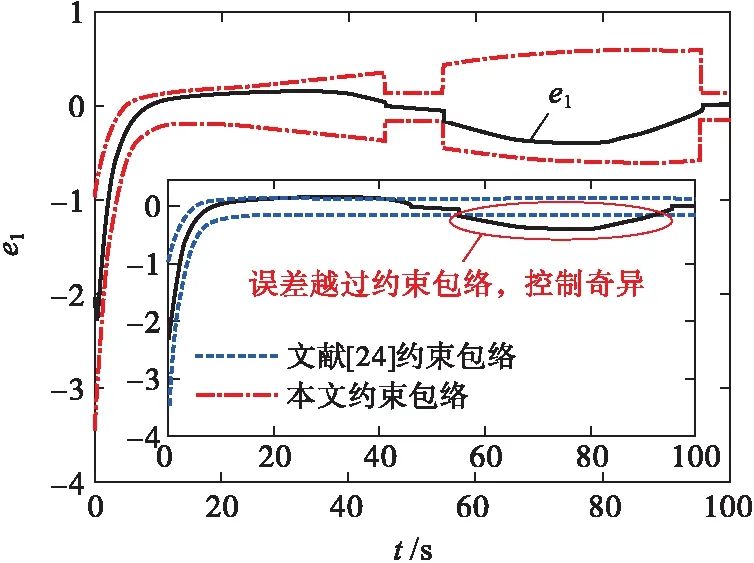
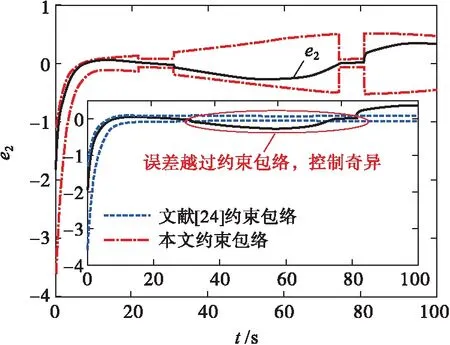
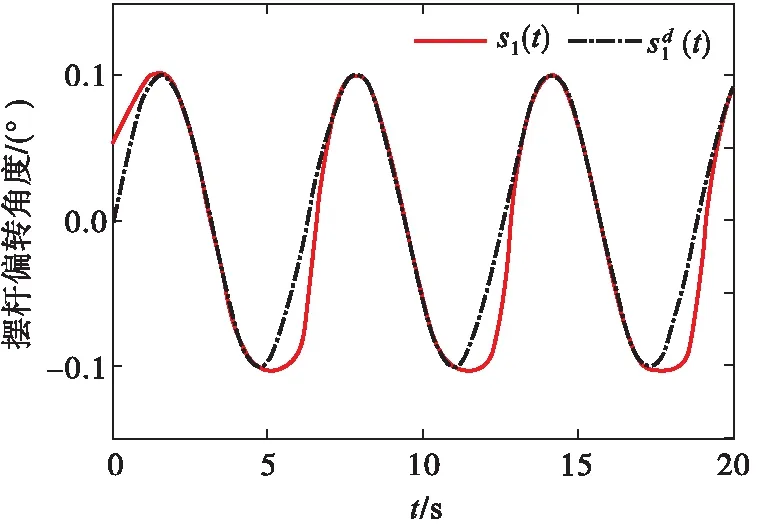
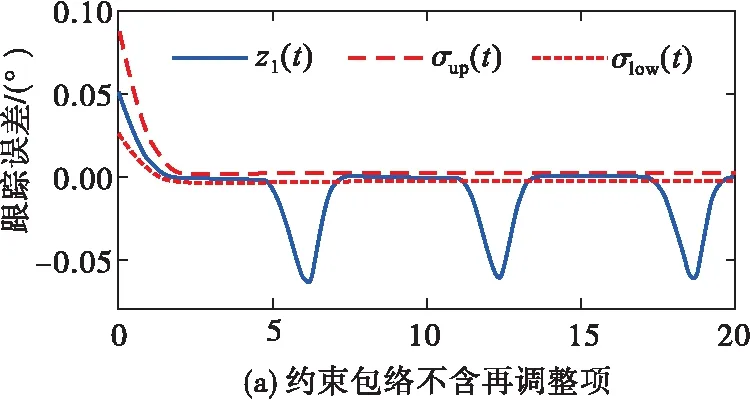
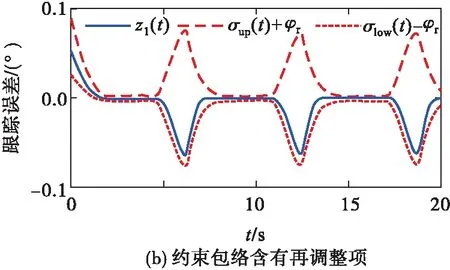
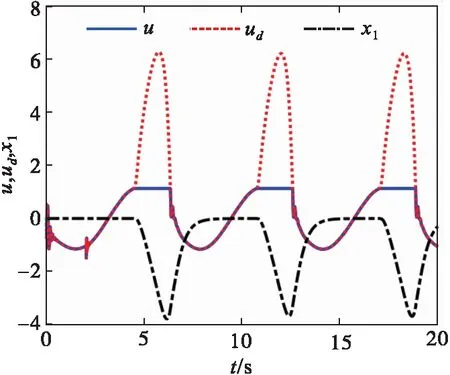
σlow(t)-φr (13) 式中: φr=c2tanh (abs(c1,1x1)) 其中,α=2,T=2,p0=π/50,pT=π/600,c2=0.2,c1,1=0.1;x1为如下辅助系统的状态: (14) 式中:Λ1(x1)=(ex1-1)/(ex1+1);a1=5。 定义转换误差Tz∈R: (15) 为s2(t)选取如下参考指令: (16) 式中:kT=1.5。 (17) 式中:kz=2。 注3:针对输入受限问题,所设计的非脆弱预设约束包络(13)含有一个自适应调整项φr∈R≥0。以x1作为感知变量,当执行器处于饱和时,有x1≠ 0,φr=c2tanh (|c1,1x1|)>0。则φr能够准确感知控制输入的饱和情况,并自适应地增大约束上包络并减小约束下包络(调整幅值为c2tanh (|c1,1x1|)),从而确保跟踪误差始终位于约束包络内,保证了预设性能的可达性,并克服了传统PPC的脆弱性缺陷。 为了验证非脆弱PPC相对于传统PPC的优越性,采用MATLAB/Simulink软件进行数字仿真,采用四阶龙格-库塔法进行求解,仿真步长均为0.01 s。 分别在以下两种情景下进行仿真。 情景1:采用文献[24]的PPC进行仿真,且不考虑外部扰动,仿真结果如图5~8所示。 情景2:采用本文的非脆弱PPC进行仿真,且考虑外部扰动,并取d1(t)=2sin(0.02πt)、d2(t)= 2sin(0.02πt),仿真结果如图9~12所示。 图5 x1对其参考指令的跟踪效果(情景1) 图6 x2对其参考指令的跟踪效果(情景1) 图7 跟踪误差e1(情景1) 图8 跟踪误差e2(情景1) 图9 x1对其参考指令的跟踪效果(情景2) 图10 x2对其参考指令的跟踪效果(情景2) 图11 跟踪误差e1(情景2) 图12 跟踪误差e2(情景2) 由图5~8可见,当没有外部扰动时,文献[24]的传统PPC能够实现x1、x2对其参考指令的精确跟踪,并且,跟踪误差e1、e2始终位于约束包络(7)内,具有满意的动态性能与稳态精度。但是,图11~12表明,当存在外部扰动时,文献[24]的传统PPC无法将e1、e2限定在约束包络(7)内,将直接导致控制奇异,表现出明显的脆弱性。图9~12表明,即便存在外部干扰,所提出的非脆弱PPC仍能有效避免控制奇异问题。当外部扰动导致跟踪误差增加时,所提出的非脆弱PPC能够自主感知误差的变化趋势,并自动调整约束包络(9),即增大上包络同时减小下包络,使得跟踪误差始终位于约束包络(9)内,满足期望的预设性能。综上所述,仿真结果充分证明了本文非脆弱PPC的有效性以及相对于传统方法的优越性,能够克服传统PPC的脆弱性缺陷。 图13 s1(t)对的跟踪效果 图14 跟踪误差 图15 控制输入与辅助系统的状态 针对现有PPC理论的脆弱性缺陷,系统阐述了非脆弱PPC新理论的基本构想。通过对传统PPC理论框架与关键技术的回顾,简要分析了导致其脆弱性问题的关键因素与作用机理。在此基础上,探讨了开辟非脆弱PPC新理论应当解决的关键基础问题。最后,给出了非脆弱PPC新方法的技术实现方案。数值仿真结果证明了所提方案的有效性和相对于传统PPC的优越性。下一步,将针对PPC脆弱性的度量问题,开展相关算法优化研究。5 数值仿真
5.1 受扰动力学系统的非脆弱PPC仿真
5.2 输入受限动力学系统的非脆弱PPC仿真
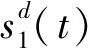
6 结语
