非概率可靠性的拉伸载荷下飞机含孔复合材料安全性分析

陈秋宇， 王 强， 史 越， 李 群， 陈玉洁

(1.空军工程大学装备管理与无人机工程学院，西安,710051；2.西安交通大学航天航空学院，西安,710049)

复合材料相对金属材料有着质量轻、比强度和比刚度高以及抗疲劳性能好等多种优点，在航空航天领域被广泛运用[1]，随着材料科学与制造工艺的进步，其用量不断提升，使用部位也从非承力结构逐步向次承力结构乃至主承力结构发展[2]。而关于复合材料与其他材料的连接方式，虽然有许多新方法被提出，但是机械连接仍是目前主要连接方式之一[3]，这导致飞机复合材料难以避免地存在穿透型圆孔，同时当较薄的复合材料层板被外物冲击击穿时，其形成的损伤也可以简化为穿透型圆孔，对材料性能产生很大影响。且由于应力集中现象的存在，含孔复合材料在拉伸载荷作用下更容易出现损伤失效，因此拉伸载荷下飞机含孔复合材料的安全性分析十分必要。

对此中外许多学者就其损伤机理及缺陷扩展[4-5]开展了大量的研究工作。但是对于飞机复合材料的实际使用而言，更加关注的是含孔复合材料是否安全的问题。相较于对复合材料微观性质的研究，根据宏观性能开展的可靠性分析能够更加有效反映复合材料的安全性。对于飞机尤其是军机复合材料可靠性研究而言，飞行训练强度的提高导致其应力区间发生变化且难以确定其分布形式，广泛应用的基于概率统计的可靠性分析方法受到数据量以及准确性影响较大[6]，不能较好地应用于飞机含孔复合材料的可靠性分析，需要更加适用的可靠性分析方法。由Ben-Haim最先提出的非概率可靠性方法可以基于较少的试验数据对可靠性进行合理的分析[7]，成功地用于不确定结构的数值分析和优化设计[8]；郭书祥基于区间模型提出了一种非概率可靠性的最小无穷范数指标[9]，在机械工程[10]等领域被广泛运用，是目前使用最多的非概率可靠性指标；王晓军等学者基于非概率应力-强度干涉模型，提出了一种体积比非概率可靠性模型，分析了与概率可靠性的相容性[11]，并较好运用到工程问题中[12]；罗阳军等人基于多椭球模型，提出一种基于“广义无穷范数”的最短距离指标，该方法相较区间模型能够考虑到变量间的相关性[13]；Sun等人针对变量边界可能存在模糊性的问题，基于模糊凸集模型提出了一种新的非概率可靠性模型，提高了非概率可靠性的适用性[14]。非概率可靠性分析方法能够很好的克服飞机复合材料结构可靠性分析中试验成本高、数据少的现实问题，因此本文基于该方法对含孔复合材料的安全性开展分析研究。

1 拉伸性能试验及结果

1.1 试验试样设计及试验方法

试验试样的材料选取某型飞机实际使用的碳纤维层合板材料，使用24层T300/5405预浸料，单层预浸料厚度为0.125 mm，铺层堆叠顺序为[0°/45°/90°/-45°]3s，采用热压罐成型工艺制作。按照《定向纤维增强聚合物基复合材料拉伸性能试验方法》规定[15]，设计无孔试样如图1所示，图中阴影部位是按照标准要求制作铝制加强片。

图1 无孔试样设计

为分析穿透型圆孔的不同孔径对复合材料安全性的影响情况，试验试样设置3种不同孔径，分别为5 mm、7 mm和9 mm，以7 mm孔径为例，设计试验试样如图2所示。

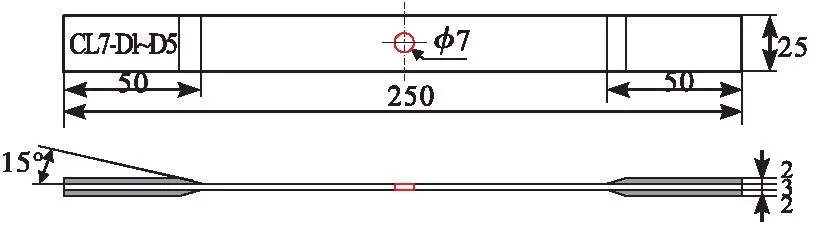
图2 含孔试样设计

按照孔径设置的不同将试样分为4组，其中每组试样各5块，各组试样的具体分组、编号和孔径设置如表1所示。

表1 分组、编号及孔径设置

试验在实验室标准环境下，采用MTS880/25T液压伺服试验机以1 mm/min的位移加载速率对试样连续加载，采用全套数字图像相关技术(digital image correlation，DIC)设备捕捉采集位移信息获取应变场。

1.2 试验结果记录

按照标准要求开展拉伸试验，记录试样破坏状态，并根据所测得的力学性能参数绘制应力应变曲线。

无孔组试样CL-A1拉伸破坏后状态如图3所示。绘制无孔组应力应变曲线后，分析发现各试样的曲线形式基本相同，因此以CL-A1试样的应力应变曲线为例，如图4所示。

图3 CL-A1破坏后的状态

图4 CL-A1试样应力应变曲线

将试验记录中反应复合材料拉伸强度与刚度的力学性能数据，即各试样的拉伸强度与拉伸弹性模量整理如表2所示。

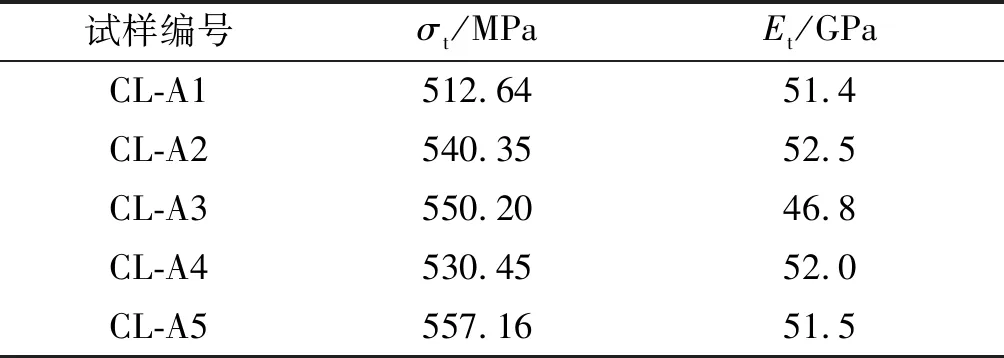
表2 无孔组(第1组)试验结果

根据第1组试验所得数据，该复合材料无穿透型圆孔时，其拉伸强度与拉伸弹性模量的平均值分别为538.16 MPa和50.9 GPa。

含孔组试样CL5-D1在试验机上被拉伸破坏时状态如图5所示。各含孔组试样曲线形式基本相同，因此以CL5-D1试样的应力应变曲线为例，如图6所示，并将各含孔组试样的拉伸强度与弹性模量整理如表3所示。

图5 CL5-D1破坏后的状态

图6 CL5-D1试样应力应变曲线

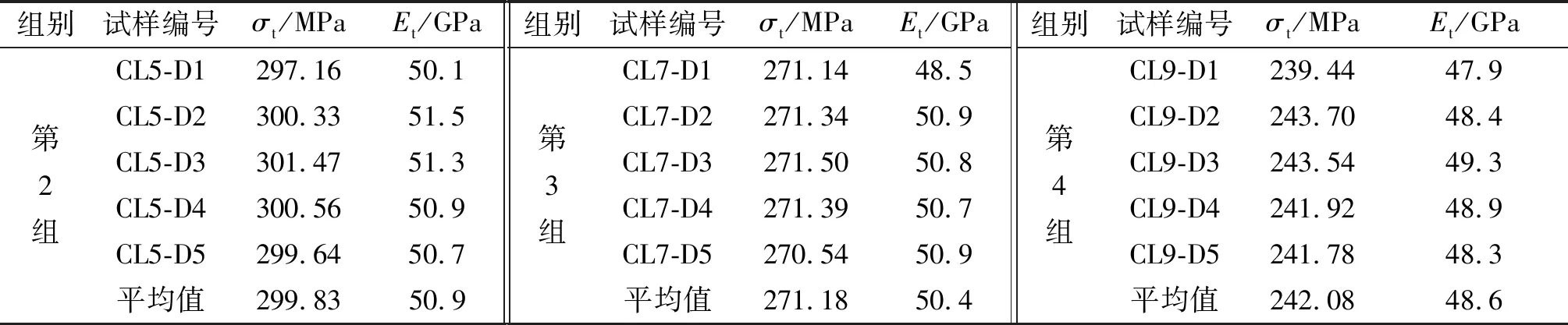
表3 含孔组试样试验结果

2 穿透型圆孔对拉伸性能的影响分析

2.1 穿透型圆孔对拉伸强度的影响分析

根据拉伸试验所得数据，以无孔组的平均拉伸强度为基准，各组的拉伸强度比值如表4所示。

表4 拉伸强度均值

对表4数据进行分析可知，孔径5 mm的穿透型圆孔使其拉伸强度均值降低238.33 MPa，降至无孔组的55.71%，孔径7 mm与9 mm的穿透型圆孔使其拉伸强度均值降低266.98 MPa与296.08 MPa，分别降低至无孔组的50.39%以及44.98%。

即穿透型圆孔会导致该复合材料拉伸强度大幅降低，且孔径越大，拉伸强度降低越严重，孔径为7 mm时甚至降低至无孔组的一半以下。观察拉伸强度比值可以发现，其降低幅度与孔径基本成正比关系。

2.2 穿透型圆孔对拉伸刚度的影响分析

根据拉伸试验所得数据，以无孔组平均拉伸弹性模量为基准，各组弹性模量比值如表5所示。

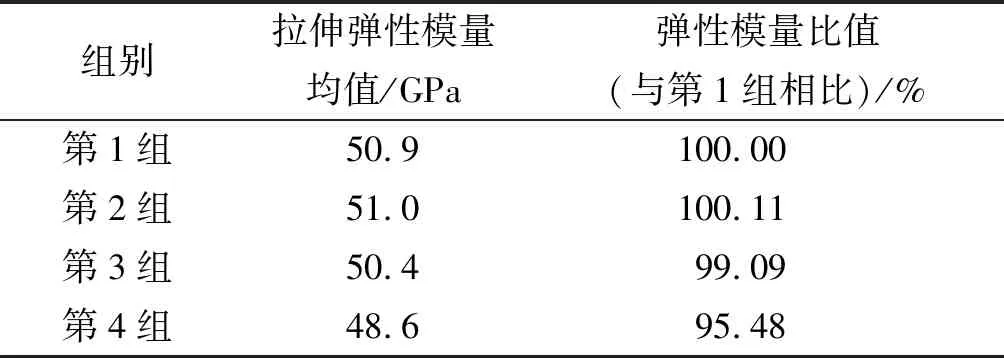
表5 弹性模量均值

根据表5数据可知，穿透型圆孔对碳纤维复合材料拉伸刚度的影响很小，孔径最大的复合材料拉伸刚度下降率也仅为4.52%。

对比穿透型圆孔对拉伸强度与刚度的影响情况可以发现，该复合材料拉伸强度所受影响较大，而拉伸刚度所受影响很小，可以忽略。且对于复合材料而言，在承受拉伸载荷作用时，决定其安全与否的根本性能为拉伸强度，因此为进一步分析拉伸载荷作用下飞机含孔复合材料的安全性，需选取合适的方法对复合材料拉伸强度可靠性进行分析。

3 含孔复合材料拉伸强度可靠性的分析

为更加直观地对拉伸载荷作用下含孔复合材料安全性进行分析，并有效反映训练强度提高对其带来的影响，选取合适的非概率可靠性分析方法，对含孔复合材料的拉伸强度可靠性进行分析。

3.1 非概率可靠性指标的选取

目前，非概率可靠性作为一种较新的可靠性分析方法，其指标尚未统一，因此在进行可靠性分析前，需要确定适合的非概率可靠性指标。目前较为常用的有最小无穷范数指标[9]、体积比指标[11]、广义无穷范数指标[13]等。

其中最小无穷范数指标基于区间模型以及区间运算方法，提出非概率可靠性指标为功能函数的均值与离差之比，其对应的物理意义为区间变量标准化后，在其扩展空间中极限状态平面至原点的最短距离，如图7所示。该指标也是目前被运用最广泛的非概率可靠性指标。

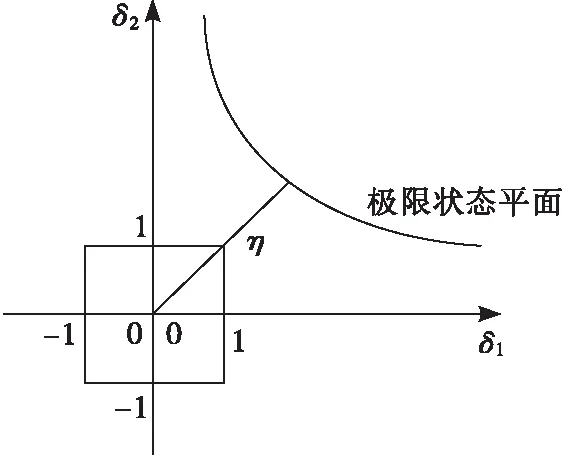
图7 最小无穷范数指标

体积比指标基于建立的应力-强度非概率干涉模型，将标准化空间内安全域面积与基本变量区域总面积的比值作为非概率可靠性指标，如图8所示。该指标物理意义较为明确且易于理解，但是在强度可靠，即可靠性指标大于1时，计算结果为1，对于判断强度是否可靠已经足够，但是在分析穿透型圆孔对复合材料的拉伸强度可靠性的影响时，无法直观看出其可靠性的变化程度以进行对比。

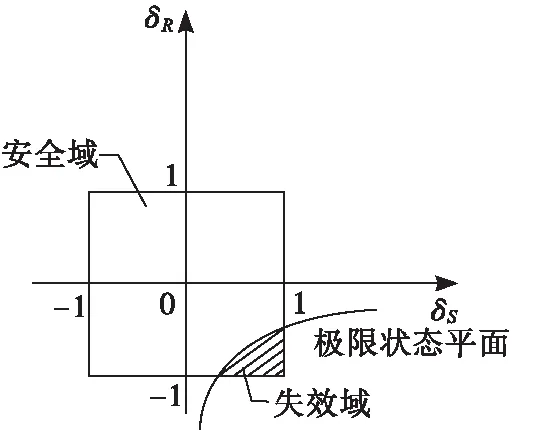
图8 体积比指标

广义无穷范数指标基于多椭球模型，定义了一种“广义无穷范数”，以此为基础计算距离，将极限状态曲面至原点的最短距离定义为非概率可靠性指标。相较于区间模型，多椭球模型能够有效考虑参数间的相关性，但相应也会有更大的计算量。

本文主要对含孔复合材料拉伸强度可靠性进行分析，受力情况较简单，且区间变量之间不存在相互关系，最小无穷范数指标足以满足分析需求，且拥有较低的计算量，因此选择最小无穷范数指标进行强度可靠性的分析计算。

3.2 拉伸强度可靠性计算

3.2.1 强度与应力的区间表示

对于承受拉伸载荷的飞机复合材料，其拉伸强度R受到材料分散性、制造工艺等影响，应力S受到飞行任务与训练强度的影响，二者都具有不确定性，可以通过区间表示法将拉伸强度区间与应力区间分别表示为：

R1=[Rl，Ru]

(1)

S1=[Sl，Su]

(2)

式中：Rl和Ru分别为拉伸强度的下限和上限，Sl和Su分别为应力的下限和上限。

对区间变量RI以及SI进行标准化变换得：

R1=Rc+RrδR

(3)

S1=Sc+SrδS

(4)

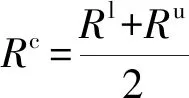
据力学试验的结果，各组拉伸强度的上下限Rl、Ru和对应的Rc、Rr整理如表6所示。

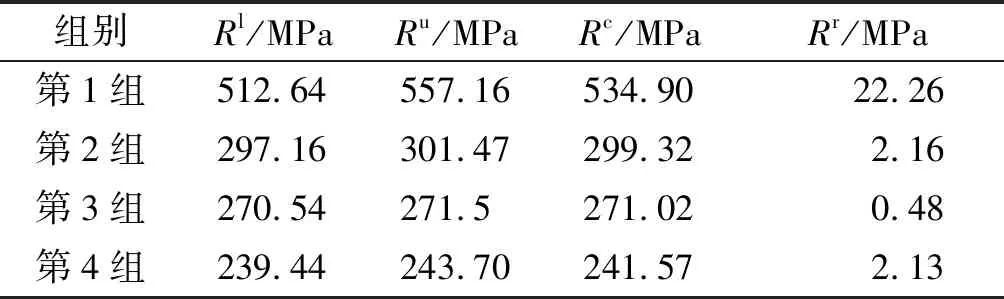
表6 拉伸强度区间数据

对于应力S，根据飞机飞行训练数据发现，飞行训练强度提高前后，该复合材料的应力区间有明显变化，训练强度提高前应力区间为Sl-∈[35.6，285]，因此，Sc-=160.3,Sr=124.7；训练强度提高后应力区间为Sl++∈ [35.6，320]，因此Sc+=177.8，Sr+=142.2，单位均为MPa。

3.2.2 极限状态函数的确定

在分析层合板的失效时，一般采用的准则主要是首层失效或末层失效[16]，而在本研究中主要依据材料宏观参数进行分析，且通过拉伸试验所得应力应变曲线可知，该碳纤维层合板在断裂失效时呈现脆性材料特征，因此在进行强度可靠性分析时，采用较简单的极限状态函数：

M=g(R，S)=R-S=0

(5)

根据式(3)、(4)对式(5)进行转换得：

(6)

式中：i=1，2，3，4，分别对应第1～4组试验数据。

3.2.3 非概率可靠性指标的计算

根据最小无穷范数指标的定义，拉伸强度非概率可靠性指标为：

ηi=min(‖δi‖∞)=min{max{|δRi|，|δsi|}}

(7)

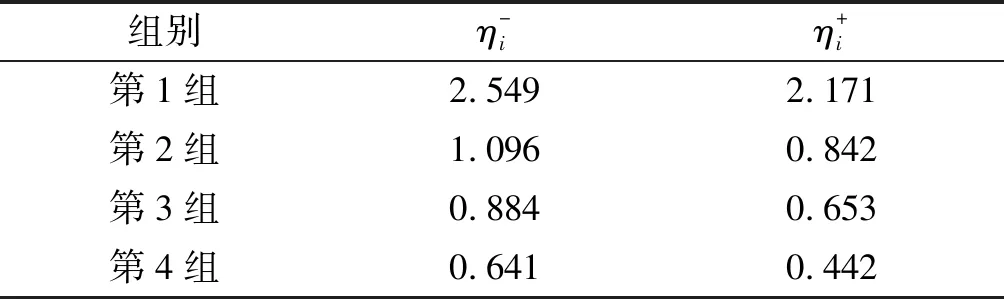
表7 各组拉伸强度可靠性指标

3.3 穿透型圆孔对复合材料安全性的影响分析

在分析材料安全问题时，可靠性在很大程度上反映着材料安全性，尤其对于飞机重要结构使用的复合材料，一旦发生失效则必然引发安全事故，此时材料的可靠性与安全性对等，因此基于非概率可靠性指标对飞机含孔复合材料安全性进行分析。

通过第1组拉伸强度可靠性指标可以看出：对于无孔试样而言，由于在设计阶段对强度有1.5倍安全系数的要求，无孔组试样在训练强度提高前后的拉伸强度可靠性指标分别达到2.549和2.171，远大于1，即此复合材料在不含穿透型圆孔时拉伸强度可靠性水平很高，能够保证飞行任务对拉伸强度的要求。

分析训练强度提高前的可靠性指标可以发现，当孔径为5 mm时，其拉伸强度可靠性指标值相较无孔试样发生大幅下降，由2.549迅速下降到1.096；当孔径增大时，其拉伸强度可靠性指标值进一步下降至1以下，其中孔径为7 mm时降低至0.884，而孔径为9 mm时甚至降低至0.641，可靠性水平大幅较低，已无法满足飞行训练对可靠性的要求，对该复合材料的安全性有较大影响。

分析训练强度提高后的可靠性指标可以发现，各含孔复合材料的拉伸强度可靠性进一步降低，分别降至0.842、0.653与0.442。其中在训练强度提高前，孔径为5 mm的复合材料的拉伸强度可靠性还可以满足训练需求，在训练强度提高后，其可靠性也同样降至较低水平，严重影响该复合材料的安全性。

3.4 复合材料安全性分析方法

根据对拉伸载荷下开孔复合材料安全性的研究，总结提出复合材料安全性分析方法。主要包括准备工作、性能分析以及安全性分析3个部分。

1)准备工作。包括确定分析对象、制作试验试样以及确定应力区间。其中分析对象指分层缺陷、穿孔缺陷、冲击损伤等损伤缺陷以及载荷模式等；确定应力区间主要根据飞机载荷谱等实际数据确定。

2)性能分析。主要开展材料级力学试验，分析损伤缺陷在对应载荷模式下对复合材料性能的影响规律，并记录强度区间，为后续安全性分析提供基础。

3)安全性分析。根据分析需求，选择非概率可靠性指标，确定复合材料失效时的极限状态函数，根据所得数据计算非概率可靠性指标，并以此对复合材料安全性进行分析。

航空复合材料安全性分析流程如图9所示。

图9 复合材料安全性分析流程

4 结论

为分析拉伸载荷作用下飞机含孔复合材料的安全性，本文根据某型飞机实际使用的复合材料，设计了无孔组和含孔组试样并开展了拉伸试验，分析穿透型圆孔对该复合材料拉伸性能的影响，并基于非概率可靠性分析了训练强度提高前后穿透型圆孔对拉伸强度可靠性的影响，得到结论如下。

1)穿透型圆孔使得飞机复合材料的拉伸强度大幅下降，孔径越大，拉伸强度下降越明显，且拉伸强度的下降率与孔径成正比关系，其中孔径达到9 mm时会使其拉伸强度下降率超过50%；穿透型圆孔对复合材料的拉伸刚度影响不大。

2)结合研究需要，确定以最小无穷范数指标作为可靠性指标对复合材料安全性进行分析。结果表明无孔复合材料拉伸强度可靠性达到2.549，可认为其安全性较高；穿透型圆孔会使拉伸强度可靠性大幅下降，且下降幅度随孔径的增大而增大，在训练强度提高前，孔径为5 mm、7 mm和9 mm的复材拉伸强度可靠性分别降至1.096、0.884和0.641，会导致该复合材料拉伸强度可靠性无法满足飞行安全的需求。

3)将训练强度提高前后复合材料拉伸强度可靠性进行对比分析，发现训练强度提高使得该复合材料拉伸强度可靠性进一步降低。在训练强度提高前，孔径为5 mm的复合材料拉伸强度可靠性尚能满足训练需要，训练强度提高后其可靠性指标也降至1以下，严重影响了该复合材料的安全性。