基于深度展开的SAR大斜视RD成像算法

陈鹭伟， 罗 迎， 倪嘉成， 熊世超

(空军工程大学信息与导航学院，西安，710077)

合成孔径雷达(synthetic aperture radar，SAR)作为一种主动传感器，可以对目标进行全天候、全天时、高分辨观测，并且具备很强的穿透性，因此广泛应用于军事和民用领域[1]。斜视SAR由于具有灵活的波束指向，相比正侧视SAR成像具备提前探测斜前视的能力，可以实现对敌方目标的实时侦察，因此研究大斜视角下的SAR成像算法具有重要的意义[2]。

斜视SAR由于波束指向与航迹不垂直，其回波信号具有大距离徙动特点，且存在距离向和方位向的严重耦合，常规的RD算法将斜距泰勒展开为低阶形式，带来了较大的误差，在方位向上的聚焦性能具有局限性，因而不能适用于大斜视角的SAR成像。改进的RD算法虽然通过二次距离压缩来提高成像质量，但在距离徙动校正、三次相位补偿过程中引入了一定的相位误差，成像质量随着斜视角的增加下降[3]。Omega-K算法虽然可以对大斜视回波信号进行较为精确的成像，但需要大量的插值运算才可以完成[4]。

近几年随着深度学习的发展[5]，基于数据驱动的智能学习方法已成功运用到SAR图像解译当中，这些方法从海量的SAR图像数据中学习得到“图像域”到“目标参数域”的非线性复杂映射[6-7]。该类方法的优点是普适性强，能够最大程度地拟合数据间的复杂映射关系，但是存在着神经网络拓扑结构设计难度大、网络参数多等问题。针对这些问题，文献[8]提出一种将算法簇深度展开为网络的方法，将乘子交替方向法(alternating direction method of multipliers, ADMM)展开成网络形式，获得了比传统 ADMM 算法更加精确的结果。文献[9]采用软阈值迭代算法(iterative shrinkage-thresholding algorithm，ISTA)设计深层展开网络，并应用于稀疏信号重构中，相比传统ISTA算法大幅提升了信号重构精度。文献[10]初步验证了深度学习方法SAR成像中的可行性，但所提方法的可学习参数少，对迭代算法的依赖性较强。

综上所述，目前虽然已有一些文献研究基于深度学习的SAR成像技术，但是这些工作的成像模式一般设定在正侧视条件下，还未有针对在大斜视条件下的SAR学习成像技术研究。因此，本文提出了一种基于深度展开网络的大斜视可学习距离多普勒(LRD)成像算法,兼顾SAR成像时间以及成像精度，同时也能够改变RD对于斜视角度的限制。

1 大斜视SAR回波信号模型分析

SAR大斜视成像系统与观测场景之间的位置关系如图1(a)所示，其中，平台的高度为h，斜视角为θ0，假设平台作匀速直线运动，速度为Vr，R0为航线与观测场景中心的最近距离，RB(t,τ;R0)为平台与点目标之间的瞬时斜距，其中t为快时间变量，τ为慢时间变量。

图1 大斜视SAR成像模型示意图

图1(b)为SAR平台与点目标的几何关系，设O点为慢时间的起点，则A点同样也是慢时间的起点，t0为波束中心穿越时刻，Rc为A点到平台的距离，则根据余弦定理可以得到平台与点目标P之间的瞬时斜距为：

RB(τ;Rc)=

(1)

假设雷达发射线性调频信号(linear frequency modulation，LFM)，调频率为Kr，脉冲宽度为Tp，则平台接收到的基带回波信号为：

(2)

式中：ξ为雷达工作波长，wa、wr分别为方位向、距离向的包络。

传统的RD成像算法是将公式(1)进行二阶近似，忽略高阶项带来的误差，直接在距离多普勒域进行距离徙动校正，经过距离压缩和方位压缩成像。算法未考虑大斜视回波信号的特点，因此不符合大斜视角条件下的成像要求。

下面将RB(τ;Rc)进行泰勒级数展开得到：

RB(τ;Rc)=Rc-(Vrτ-Ynsinθ0+

(3)

从式(3)可以看出，线性项为距离走动项，高次项为距离弯曲项，当斜视角足够大时，高次项的值很小，因此可以忽略距离弯曲对包络的影响。结合式(2)、(3)可以看出距离弯曲项和雷达波长处于同一个数量级，因此不可以忽略距离弯曲对回波相位的影响。

下面将回波信号变换到距离频域上，忽略两个维度的信号包络，对其进行距离走动校正和距离向脉冲压缩。

走动误差为:

ΔRw=Vrτsinθ0

(4)

构造的匹配滤波函数为:

(5)

式中：fr为距离向频域；f0为雷达工作频率。此时，经过走动校正、距离压缩后的回波信号，多普勒中心的频率搬移到零频，因此雷达发射波束的中心线位于零多普勒平面。经过以上操作得到的回波信号为：

(6)

其中:

(7)

(8)

经过压缩后的信号，距离向和方位向的耦合程度大大降低，但仍存在着残余距离徙动以及距离弯曲项对相位的影响。改进的RD算法在二维频域上分别构造二次距离压缩、三次相位补偿函数以及方位向脉冲压缩函数解决上述问题，具体构造方法可参考文献[3]，本文不再赘述。改进的RD算法在构造上述压缩函数和补偿函数时均采用了不同程度的近似，当斜视角增大时，其成像精度和质量逐渐下降。

2 大斜视SAR LRD成像网络

2.1 成像网络构建

针对第1节大斜视SAR成像存在的问题，本文通过深度学习的方法，将二次距离压缩、三次相位补偿函数H2和方位脉冲压缩函数H3作为可学习的参数，通过网络学习得到相比传统算法更加精确的成像矩阵，从而提高成像精度、改善聚焦效果。为了更好地描述可学习参数与成像结果的关系，结合式(2)、(5)以及文献[3]将大斜视SAR的RD成像算法过程写成矩阵相乘的算子形式：

(9)

(10)

式中：*表示矩阵共轭操作。根据式(9)、(10)的分析，SAR成像可以看作为一个线性求解的逆问题，该二维观测模型可以通过求解最优化问题得到:

(11)

其中λ‖Θ‖p为正则化约束项，λ为正则化系数。式(11)的求解依靠迭代优化算法(如ISTA、AMP)实现，这些传统算法要求其中的矩阵M-1是精确已知的，并且在迭代过程中，迭代参数的选择需要通过人工进行多次调试才能获得较好的解，这无疑提高了计算复杂度和时间成本。

本文所构建的LRD成像网络是建立在式(9)的大斜视SAR二维观测模型的基础上，将式(11)的求解算法深度展开成网络形式。需要注意的是，由于网络中成像矩阵H2、H3是可学习的矩阵，式(11)的求解在成像网络中不再是一个线性问题，而是一个复杂的非线性求解问题，因此需要在网络中添加非线性变换实现回波信号到SAR图像的非线性拟合。以ISTA算法求解式(11)为例，ISTA算法主要分为残差计算、算子更新以及软阈值迭代3个步骤，因此在深度展开网络中，同样在网络的第k层(k=1,2,…,K)构建相应的3个子网络层，具体描述为：

1)残差层：用R表示，该子网络层用来计算残差，在成像网络的第k层中，通过第k-1层输出的场景散射系数计算关于大斜视回波信号的残差，具体的表达式为

(12)

2)算子更新层：用P表示，该子网络层的输入为残差层计算得到的残差，并作用于M，具体表达式为：

(13)

(14)

式中：β为迭代步长，在传统ISTA中每一次迭代中，β的值是固定的，而在成像网络中是一个可学习的参数。

3)非线性变换层：用F表示，该子网络层用来体现成像网络的非线性映射能力，通过对算子更新层得到的进行非线性变换，获取大斜视SAR回波信号到场景散射系数的非线性映射能力，同时输出下一层的场景散射系数。具体表达式为:

(15)

F(P(k);λ,T)=soft(P(k);λ,T)=

sign(P(k))(|P(k)|-T)

(16)

式中：F(·)为成像网络的非线性变换；soft(P(k);λ,T)表示与正则化参数λ有关的软阈值函数；sign(·)通常为符号函数，在所构建的成像网络中，将其直接作为非线性变换层的激活函数，T为迭代阈值。该网络层可学习的参数可以为迭代阈值T，正则化参数λ。

综上所述，所构建的大斜视SAR LRD成像网络的单层拓扑结构由残差层、算子更新层、非线性变换层3个子网络层构成，并且可学习的参数集为Ω={H2,H3,β,T,λ}。需要说明的是，在网络训练过程中为了减小网络学习参数的规模，成像矩阵H2、H3仅在一轮反向传播训练后发生变化，迭代参数β、Τ、λ在每一层中则是可变的。图2和图3分别给出了所构建网络的整体网络拓扑结构以及单层拓扑结构。其中单层的拓扑结构由迭代算法中一次迭代过程决定，整个大斜视SAR LRD成像网络包含具有相同的拓扑结构的k层。

图2 大斜视SAR LRD成像网络结构示意图

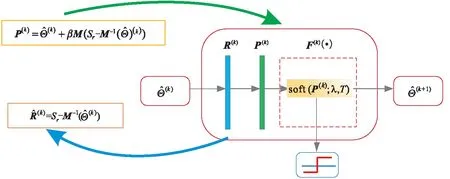
图3 第k层网络结构示意图

2.2 网络数据生成与训练

一般来说，雷达观测场景是未知的，无法直接对回波样本中添加有关场景散射系数的标签数据；另一方面，由于网络性能受到监督训练的标记训练样本的限制，如果采用监督的训练方法，并根据常规的大斜视SAR成像结果进行标记，则该网络的性能受到常规成像方法的限制。因此，本文采用非监督的训练方式对成像网络进行训练。

回波样本生成方面，由于样本生成是训练和测试前的预处理，是可以离线完成的，因此样本生成的准确性比时间开销和计算负担更重要，同时，由于完全准确的真实散射信息难以获得，实际测量数据很难建立有效的样本集，为了得到较为精确的回波样本集，本文采用理想的随机点散射模型并根据式(2)的回波信号模型生成大斜视SAR回波，并加入系统环境噪声，在不改变SAR成像模型的情况下生成大量回波数据样本。设定回波样本数量为N，回波样本集Sn={S1,S2,…,SN}，其中n=1,2,…,N为回波样本序列号。

在回波样本集构建完毕之后，通过设计损失函数实现非监督学习，对网络进行误差反向传播时，因为采用的是非监督学习，无法直接度量网络的输出与真实场景散射系数之间的差异，而是直接利用网络最后一层得到的场景散射系数估计值作用于M-1，得到SAR回波的估计值并与真实回波进行对比。其回波估计值表达式如式(17)所示，设定损失函数为均方误差函数(mean square error，MSE)，具体如式(18)所示:

(17)

(18)

在网络训练过程中，可学习参数集Ω的训练实质上是在求解优化损失函数的最小化。这可以通过许多现有深度学习优化器来实现，包括梯度下降、时间反向传播等。需要注意的是，由于大斜视SAR回波是复数据，但在成像网络中数据均为实数传播，因此，所构建的网络可以采用基于随机梯度下降的Adam优化器进行训练。同时为了防止在训练成像网络过程时出现梯度消失情况，将学习率设定为较小的值，在满足条件的同时，收敛的速度尽量快。

3 仿真实验与分析

本节将采集得到的大斜视SAR回波数据作为样本，并仿真在噪声环境下对成像性能的影响，对仿真数据进行成像验证。同时为了验证所提算法的优越性，将其与改进后的RD算法以及传统ISTA算法进行比较，需要注意的是，在与ISTA比较时，我们将ISTA的迭代次数设置为与所提成像网络的网络层数相等。

3.1 点目标仿真实验

首先对噪声环境下的点目标成像性能进行验证。成像模式为条带模式，观测场景内包含有3个目标散射点。

在生成训练样本和测试样本方面，通过加入随机加性高斯白噪声产生1 000个回波样本，信噪比的范围为-15～30 dB，并且随机选取样本数量的70%作为训练样本，30%作为测试样本。

在训练阶段，对于网络参数的初始化，根据文献[3]将成像矩阵H2和H3初始化，进一步得到Θ0，对迭代参数初始化λ0=0.8,β0=0.8，T0=0.5，得到初始化参数集Ω0。设定学习率为η=0.001、batch size设置为4，整个样本集的训练次数(epoch)设置为1 000，训练样本Ntrain= 700。

在测试阶段，测试样本为Ntest=300，对测试样本集取平均得到最终的成像结果。最终成像时，将网络学习得到的成像矩阵H2及H3、迭代步长、正则化参数、迭代阈值作为固定值输入成像网络，成像过程就转化成一次网络的前馈运算，可以直接输出成像结果。表1给出仿真对应的雷达参数以及网络参数。

表1 雷达参数和网络参数

本文所提方法采用Python、Tensorflow1.14实现成像网络模型，所有实验均在一台个人电脑(Intel i7-10875H，16GB RAM)上完成，并且利用一块英伟达Geforce RTX 2060显卡进行GPU加速。图4给出不同网络层数下训练集的损失函数曲线图，可以看出，网络在训练到50次左右时开始收敛，误差逐渐趋于0，随着网络层数的增加，网络的收敛速度变慢，误差的振荡幅度在前50次训练逐渐变大。为了平衡网络的误差以及网络大小之间的关系，本文的仿真实验均设置网络层数为8层。

图4 不同网络层数的误差曲线图

设定雷达工作在X波段(0.03 m)，点目标在距离向和方位向均相距30 m，场景中心点与载机航迹的最近距离为10 km，图5给出在信噪比15 dB条件下，不同算法的点目标成像结果对比图。需要注意的是，大斜视条件下，成像之后点目标的位置在距离向和方位向上均存在着偏移，因此需要进行几何校正。图5是经过几何校正之后的结果，本文采取的几何校正方法为文献[11]，这里不再赘述。由图5可以看出，3种算法均能够对点目标进行正确成像，改进的RD成像算法点目标周围旁瓣较高，且当目标相距不远时，容易在旁瓣交叉处形成虚假目标；L2范数ISTA虽能够有效抑制旁瓣，但需要手工调试参数才可以满足成像要求，而本文方法可以将学习到的参数输入成像网络直接成像，实现点目标的精确聚焦，体现出良好的成像性能。同时，本文方法在斜视角较大的情况下仍可以有效适用。

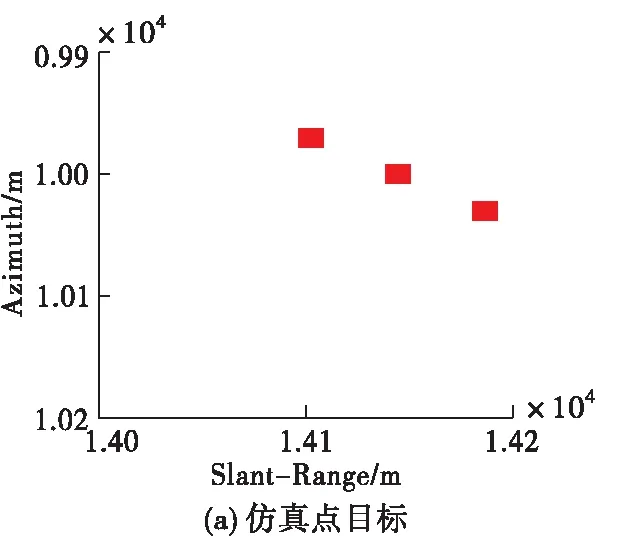
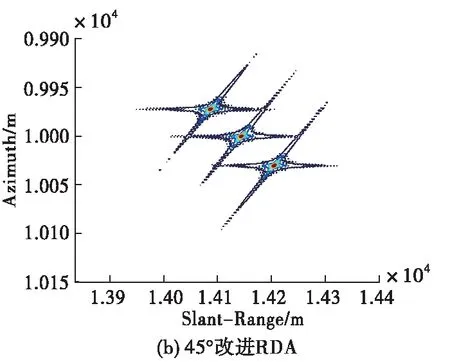
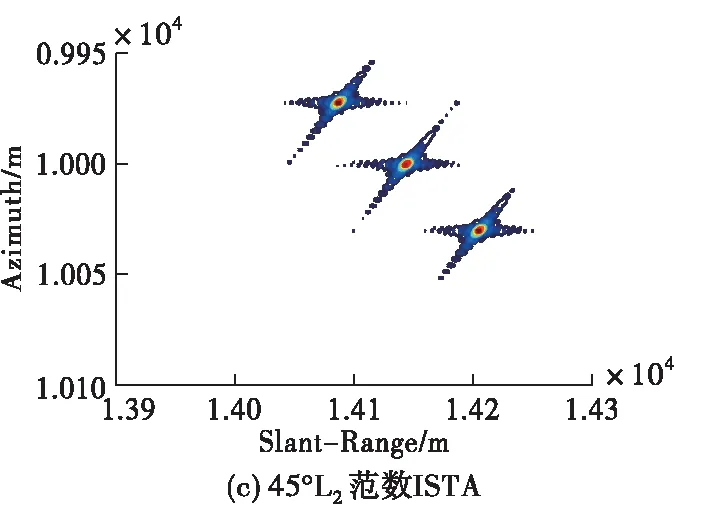
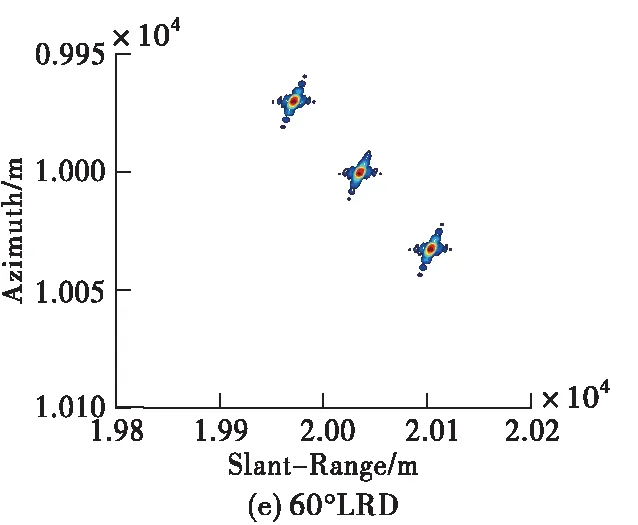
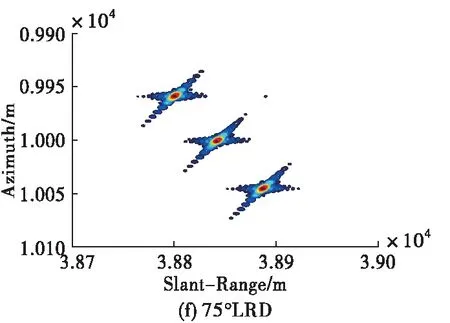
图5 15 dB信噪比条件下点目标成像结果对比

3.2 算法对比分析

为了展示所提成像方法的优势，现将所提方法与传统大斜视成像算法(如Omega-K、NCS)做对比，需要说明的是，由于其它成像算法均为采取插值操作，为了方便与其它算法进行对比我们对点目标仿真时采用的是无须Stolt插值的近似Omega-K算法[12]，仿真条件设置为15 dB信噪比、斜视角为45 °条件下，其余参数均与表1相同。对比结果如图6所示。从图中可以看出，本文方法抑制旁瓣的效果相比于Omega-K算法、NCS算法更好，展示了较好的成像性能。

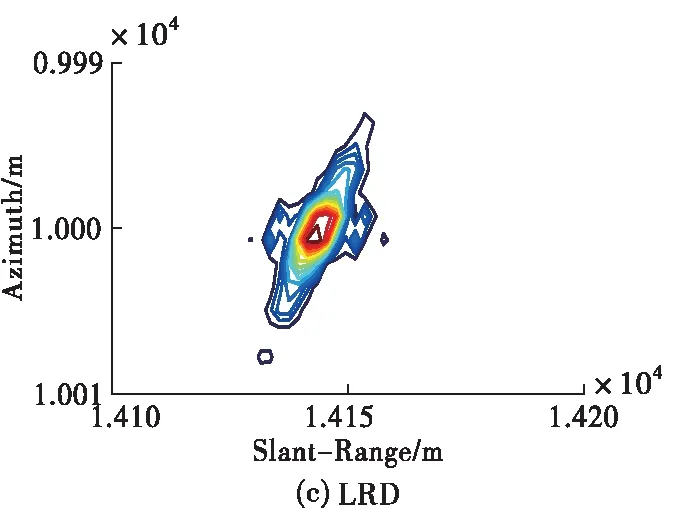
图6 不同算法的点目标仿真结果

由于所提方法在经过网络深层迭代之后，其所有参数均已固定，此时当输入大斜视SAR回波时，网络相当于进行一次前馈运算即可得到SAR成像结果。因此在计算其运算量时[12]，实际上仅需计算式(9)中所涉及的操作即可，其包括距离向FFT、方位向FFT、复数相乘、距离走动校正、2次距离压缩和3次相位补偿等。假设估算浮点运算量(FLOP)的参数分别为：输入距离线数Nri=4 096，每一输入距离线上的采样点数Nrg=4 096，每一输出距离线上的采样点数为Nro=3 072。

因此所提方法中涉及到的距离向FFT的浮点运算量GFLOP = 5NriNrglog2(Nrg)/109≈ 1.01，方位向FFT的GFLOP=5NroNrilog2(Nri)/109≈ 0.76；复数相乘的GFLOP=6NriNrg/109≈ 0.10；2次距离压缩及3次相位补偿的GFLOP=12NriNro/109≈ 0.16。从而计算出所提方法总的运算量为4.48GFLOP，在回波数据大小相同的条件下，近似Omega-K算法总运算量为3.95GFLOP，NCS算法总运算量为6.34GFLOP，L2范数ISTA算法的运算量为48.26GFLOP。

同时为了定量对比所提方法与传统成像算法的成像性能，分别采用峰值旁瓣比(peak side lobe ratio，PSLR)，积分旁瓣比(integral side lobe ratio，ISLR)来进行衡量，需要说明的是，这些指标均为场景中心点目标经过计算得到。为了比较成像时间，对所有算法均成像50次取平均值，其结果如表2所示，所提方法在PSLR、ISLR等指标较传统算法有明显提高，并且所提方法的成像速度与传统算法处以同一数量级，而较ISTA算法成像速度快。综合来看，所提方法相比传统成像算法能够同时兼顾成像效率以及成像精度。

表2 45°斜视角、15 dB信噪比条件下不同算法成像质量评价指标结果对比

3.3 面目标仿真实验

为了进一步说明本文方法的有效性，下面对面目标进行仿真验证。其中面目标的仿真涉及到的雷达参数以及网络参数设置与点目标仿真实验一致，回波信号同样加入系统环境噪声。场景的大小为100 m×100 m，网络输入回波矩阵S的大小为300×484，实验仍与RDA、L2范数ISTA等传统算法作对比，图7给出了仿真实验结果对比图。从图可以看出，改进RD成像算法在面目标成像时旁瓣较高，并且还存在着距离/方位的交叉耦合，传统ISTA虽能有效抑制旁瓣，但是算法迭代成本较高。而所提的方法既可以有效完成距离/方位的解耦、抑制旁瓣，对于一些重点目标也能够精确成像，得到较为理想的成像结果。

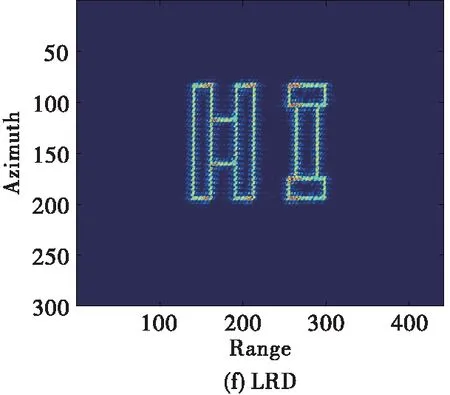
图7 45°斜视角、15 dB 信噪比条件下仿真面目标成像结果对比

4 结语

针对大斜视SAR的回波信号具有严重的距离/方位耦合，大距离徙动等特点，本文首先对大斜视SAR回波信号进行分析，而后确定成像网络所需学习的参数，建立大斜视SAR二维成像网络模型，然后通过学习训练得到较为精确的成像矩阵以及迭代参数；最后，将回波数据、学习到的参数直接输入到成像网络中，输出质量较好的SAR图像。通过具体的点目标和面目标的仿真实例，对本文所提方法的正确性和有效性进行了分析和验证。仿真结果表明，所提方法对于提升大斜视角下的SAR成像性能具有良好的效果，成像精度相比于改进的RD算法、传统大斜视成像算法也有了进一步的提高，满足大斜视条件下的成像要求。