INS辅助的BDS伪距率一致性欺骗信号检测方法

常浩伟， 庞春雷， 张 良， 郭泽辉， 吕敏敏， 吴 强

(1.空军工程大学信息与导航学院，西安，710077；2.95801部队，北京， 100089；3.95894部队，北京， 102200)

欺骗式干扰通过转发或自主产生与真实信号高度相似的欺骗信号[1]，诱导北斗卫星导航系统(BeiDou navigation satellite system，BDS)实现错误定位，给生产生活带来了严重危害。针对欺骗式干扰采取有效的欺骗检测技术，是提高导航安全性的重要手段[2-3]。

目前常见的欺骗检测技术分为两类。第1类主要针对欺骗信号观测值进行检测，寻找其与真实信号之间的差异。包括基于信号功率的检测技术[4]，基于多天线的检测技术[5]，基于观测量一致性检验的检测技术[6-8]。第2类技术依据真实信号与欺骗信号相互作用后，接收机输出结果的异常变化来检测欺骗。主要包括基于信号质量检测[9-10]，基于跟踪环路相关输出异常检测[11]等方法，不足之处在于遇到零陷攻击后，真实信号和欺骗信号将无法相互作用，导致检测方法失效。上述方法主要依靠卫星导航自身信号进行欺骗检测，但仍存在一定的缺陷。而惯性导航系统(inertial navigation system，INS)不受欺骗干扰环境的影响，能够为导航提供可靠的信息，可用于辅助北斗欺骗干扰信号的检测。文献[12]验证了高精度下的惯导能够用于辅助GNSS进行欺骗干扰识别；文献[13]在已知天线基线矢量的情况下，利用INS提供的姿态信息，构造载波相位双差检验统计量；文献[14]提出利用惯导辅助三元天线阵进行欺骗干扰检测。

因此，本文提出一种由INS辅助BDS进行伪距率一致性检测的方法。利用INS速度信息构造校准后的伪距率，与卫星实际解算的伪距率作差得到欺骗检验量，并从故障检测的角度出发，制定了欺骗信号检测步骤，最后通过仿真验证了相同惯导精度辅助下的伪距率模型检测准确率明显优于伪距模型，能够用于检测拉偏较小的速度欺骗。

1 转发式欺骗干扰基本原理

北斗卫星真实信号伪距观测方程为：

ρ(j)=r(j)+δtr-δt(j)+I(j)+T(j)+ε

(1)

式中：δtr表示接收机钟差造成的位置误差；δt(j)表示卫星j钟差造成的位置误差；I(j)和T(j)分别表示电离层延迟和对流层延迟；ε为观测噪声；r(j)表示卫星j到接收机的几何距离，在地心地固坐标系中可表示为：

(2)

式中：(x(j),y(j),z(j))为实际观测到的卫星坐标；(x,y,z)为地面接收机坐标。

利用四星定位原理，当同时存在4颗及以上卫星信号时，通过获取星历信息解算卫星的位置坐标(x(j),y(j),z(j))，代入式(1)和式(2)，采用最小二乘法进行解算，得到接收机位置坐标(x,y,z)，实现定位要求。

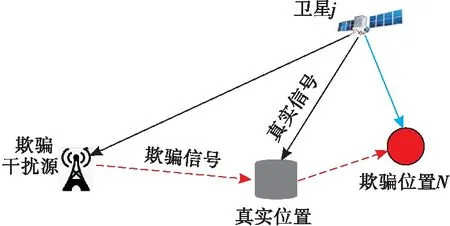
图1 转发式欺骗原理图

当存在转发式欺骗干扰时，转发式欺骗干扰源截取卫星真实信号后，经过信号延时、功率放大等处理后，再转发出去，诱骗接收机进行错误的定位，从而达到欺骗干扰的目的。如图1所示，由于欺骗信号源的存在，北斗卫星伪距观测方程变换为：

(3)

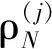
(4)

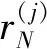
联立式(3)和式(4)，可得受到欺骗后的伪距观测方程：

(5)

2 INS辅助的BDS伪距率一致性欺骗信号检测

2.1 构造欺骗信号检验量

对式(1)用时间求导，可得：

(6)

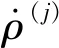
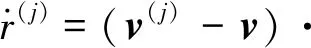
(7)

式中:v(j)为卫星j运行速率;v为接收机速率;1(j)为卫星到接收机的单位观测矢量。

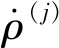
(8)

在实际观测过程中，电离层延迟和对流层延迟对时间变化的敏感度不高，故其延迟变化率可忽略不计。结合式(6)和式(7)可得：

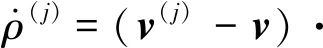
(9)

式中:

δf(j)=af1+2af2(t-toc)

(10)

式中:af1、af2为卫星钟差二项式系数;toc为标准时间，具体数据均能从导航电文中得到。

同理，当存在欺骗干扰时，

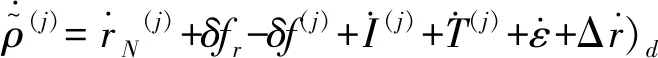
(11)

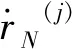
(12)

代入式(11)中，可以得到：

(13)

分析式(9)与式(13)可以发现，经过转发器的延时处理后，会产生附加伪距率，导致观测值出现定位跳变现象。

INS不受卫星欺骗干扰的影响，可以为导航提供可靠的信息。利用加速度计和陀螺仪分别输出速度增量和角度增量，通过对时间的积分，获得接收机在k时刻的速度为:

(14)

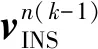
(15)

(16)

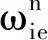
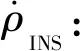
(17)

式中:G为地心地固坐标系到“东北天”坐标系下的转换矩阵。

通过与卫星实际测量得到的伪距率相减，从而构造出统计检验量:

(18)

2.2 一致性欺骗检测

(19)

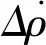
(20)

则H1成立(存在欺骗干扰)的条件为：

(21)

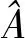
(22)

(23)

当H0成立时，T～t(k-1),且λ(x)是|T|的单调增函数，故:

p{λ(x)≥γH0成立}=P{|T|≥γ1H0成立}=α

(24)

得到临界值:

(25)

因此，欺骗信号一致性检验的判决门限可以表示为:

(26)

相应的虚警率PFA和最小检测概率为PD(最大漏检概率PMD=1-PD)为:

(27)

式中:P0、P1分别为H0、H1成立下的概率分布函数。

通过故障检测的理论对其进行分析，结果如图2所示。

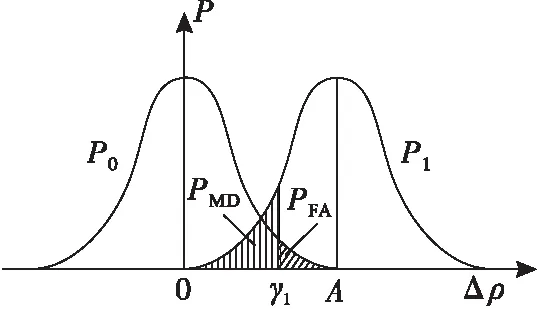
图2 BDS欺骗检测概率分析

对欺骗信号的检测步骤如下：

1)已知虚警率PFA，利用真实信号概率密度分布曲线P0，计算得到欺骗信号检测门限γ1；

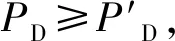
3 仿真实验

为验证惯导辅助的北斗速度/伪距率一致性检测方法的有效性，利用导航信号源、欺骗干扰源和组合导航接收机等设备搭建欺骗干扰环境，通过解算的北斗伪距率和惯导速度信息构造一致性统计检验量，以此实现对欺骗干扰信号的检测。

3.1 仿真条件设定

仿真设置载体运动时间为1 750 s，分别模拟了载体在不同时刻的运动状态。设置载体运动初始状态见表1。

表1 载体初始状态

根据轨迹模拟代码预设的飞行姿态参数，模拟出的运动轨迹，如图3所示。

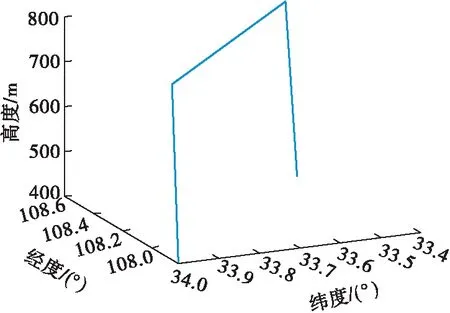
图3 运动轨迹图

如图4所示，连接导航信号源、欺骗模拟源、组合导航接收机以及计算机，搭建欺骗干扰平台,平台参数见表2。将无人机运动数据导入信号源中，然后通过欺骗模拟源人为设置欺骗干扰，分别采集在真实情况和欺骗情况下的BDS信号和INS信号，获得观测值数据。

图4 设备连接图

表2 仿真参数设置

为验证本文所提方法对不同欺骗干扰信号的检测性能，利用欺骗模拟源设置不同类型的欺骗干扰方案，欺骗干扰模式设置如表3所示。为保证欺骗信号能够对信号源实施有效干扰，设置欺骗干扰源位置于东经108.1°，北纬33.9°，高度400 m，信号输出功率为-20 dB。

表3 欺骗方案设置

3.2 实验结果分析

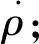
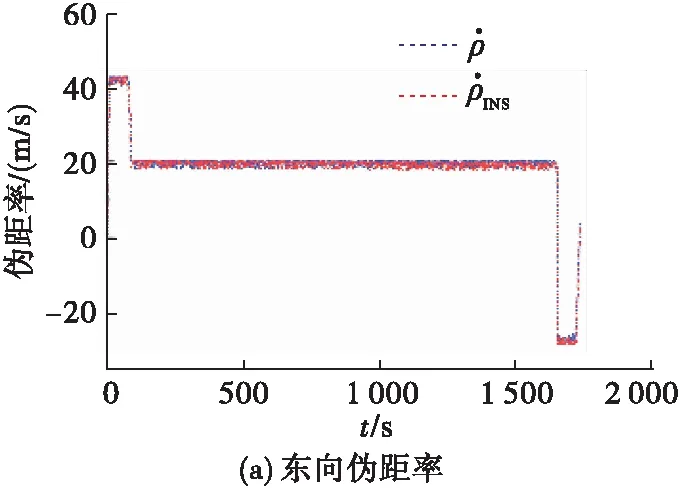
图5 真实信号下INS校准前后伪距率关系

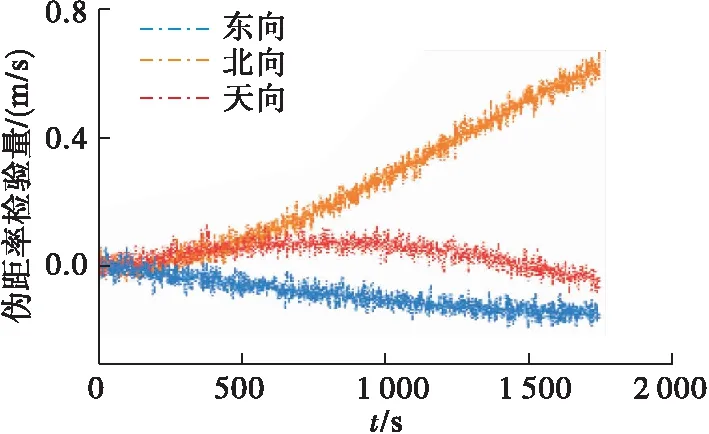
图6 伪距率检验量误差分布曲线

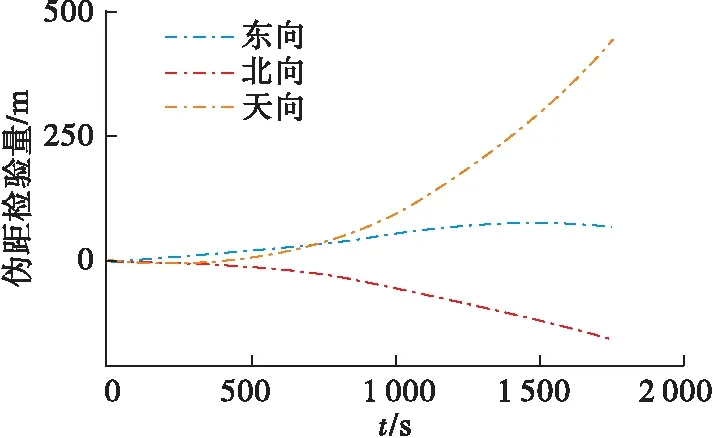
图7 伪距检验量误差分布曲线

如图8所示，在1 750 s内，基于伪距率构造的检验量模型的概率密度分布曲线满足正态分布的要求。考虑到INS解算得到的速度误差同样会随着时间不断积累，导致检验量在时间域上呈现发散趋势，且高度通道检验量发散趋势更为明显。故本实验中仅对前200 s的东向和北向检验量进行处理，获得真实信号下的概率密度函数，并设置虚警率PFA=0.01，最小检测概率为PD=0.9。根据概率密度分布曲线得到欺骗干扰信号检测门限：东向检验量为0.207 1 m/s，北向检验量为0.136 6 m/s。

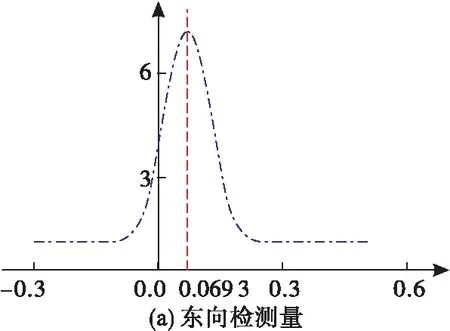
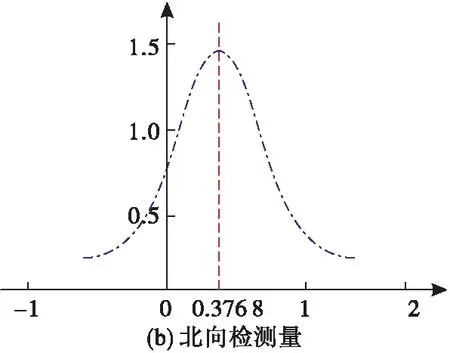
图8 检验量概率密度分布曲线

根据表3提供的欺骗方案进行欺骗干扰，通过设置欺骗模拟源依次对接收机施加方案2、3、4中的欺骗干扰策略。利用伪距率构造的检验量对欺骗干扰信号进行检测，检测结果如图9所示。

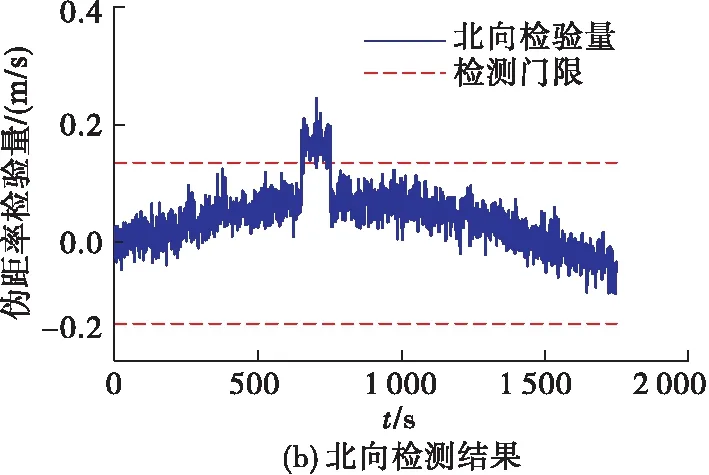
图9 欺骗状态下伪距率检验量误差曲线

若采用伪距模型进行欺骗检测，则需要INS位置信息反解得到经INS校准后的伪距参考值，与卫星实际测量得到的伪距作差，得到伪距一致性检验量。利用前200 s内的概率密度函数获得伪距检验量的检测门限：东向检验量为58.595 1 m，北向检验量为58.148 1 m。然后对运动载体分别施加表3中方案2、3欺骗干扰策略，利用伪距检验量构造的检验量对欺骗干扰信号进行检测，检测结果见图10。

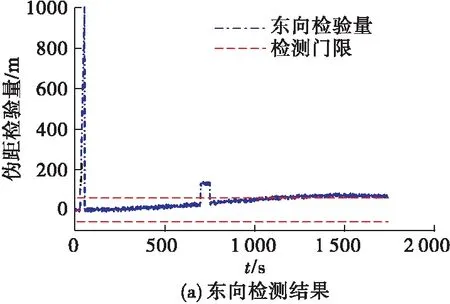
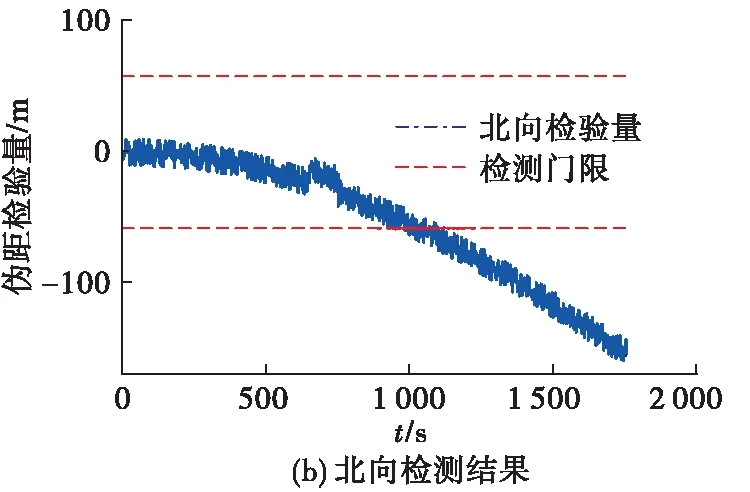
图10 欺骗状态下伪距检验量误差曲线

对于伪距模型检测结果，在25～50 s内，载体受到了模式2设置的悬停静止欺骗，使伪距检验量向东偏移1 000 m左右，超出了检测门限；当运动时间为700 s时，欺骗干扰源诱骗载体向东拉偏100 m，导致检验量超出门限值。但随着时间的增长，由于惯导位置误差的不断积累，伪距检验量在未受到欺骗干扰的情况下也高于检测门限，无法对后续的欺骗干扰进行有效检测。同时，采用伪距模型无法对缓慢的速度拉偏做出有效检测，导致出现漏警现象。

3.3 不同模型检测性能比较

为进一步验证本文所提算法的有效性，对模拟信号源产生的100组不同轨迹、不同运动时间的载体施加表3中的欺骗策略，利用表4所示不同精度的惯导设备提供的惯导信息辅助进行欺骗检测，获得不同模型在不同轨迹下的误警个数与误警率，取均值后得到最终检测结果见表5。

表4 INS误差参数

表5 欺骗检测结果

可以看出，高精度的惯导系统辅助进行欺骗检测时，检测性能明显优于低精度惯导。相较于伪距模型，伪距率模型受惯导漂移误差的影响较小，在欺骗检测过程中能够保证较高的检测准确率，其中，N1精度下东向检验量误警率降低了26.34%，北向检验量误警率降低了29%；N2精度下东向检验量误警率降低了35.27%，北向检验量误警率降低了36.94%。随着时间的推移，两种检测模型均出现误警现象，选取不同运动时间的轨迹，得到误警率随时间变化的曲线，见图11。

从图11可以发现，随着时间的增长，较低惯导精度的伪距模型率先发生误警现象，300 s之后，较高惯导精度的伪距模型检测准确率同样出现偏差，并且由于受到惯导误差发散的影响，基于伪距的欺骗检测模型误警率逐渐增大，严重影响检测精度；而基于伪距率的检测模型即使是在较低精度的惯导系统辅助下，误警出现时间也在伪距模型之后，且相较于伪距模型，误警率增长趋势也较为缓和。

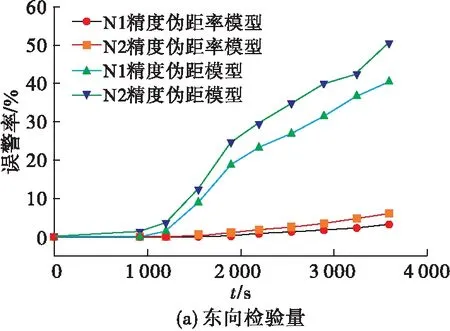
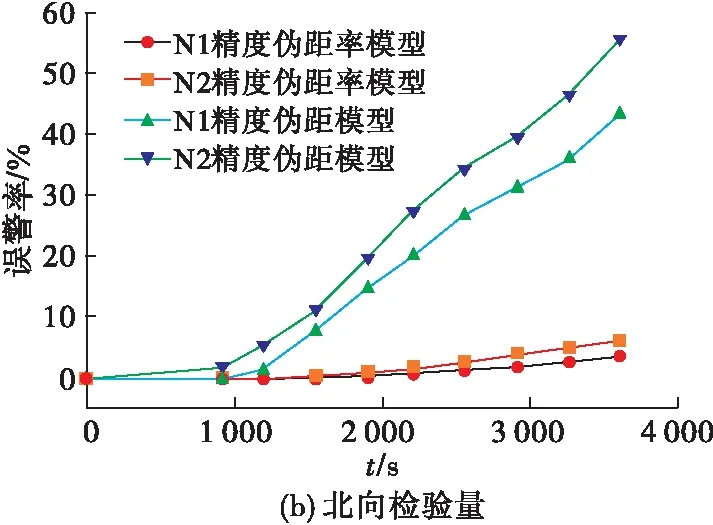
图11 误警率变化趋势

4 结语

本文针对北斗卫星导航中面临的欺骗干扰问题，提出利用INS的速度信息辅助BDS进行伪距率一致性检验。该方法利用真实状态下INS反解与BDS实测下的伪距率信息高度一致的特点，构造检验统计量，并依据故障诊断的方法对欺骗信号进行有效检测。实验结果表明，两种检测模型检测性能均受到惯导精度的影响。相较于同精度惯导辅助的伪距模型而言，伪距率模型能够保证较长时间内的高精度检测，且敏感于拉偏缓慢的速度欺骗。当INS速度严重发散时，可利用历史数据或缩短检测周期可以提高检测性能。