基于MFO-HTN的超视距空战战术机动组合规划

闫孟达, 俞利新, 左家亮, 张 滢, 胡东愿, 岳龙飞, 杨任农

(空军工程大学空管领航学院，西安，710051)

空战机动决策一直是军事领域的热点问题之一。空战机动决策的研究方法主要有专家系统[1-2]、矩阵对策[3-5]、优化理论[6]、模糊推理[7-8]和人工智能[9-14]等方法。文献[1～2]在专家系统的基础上结合滚动时域、模糊规则等方法，解决专家系统不够灵活、不可拓展的问题。矩阵对策法需要对当前态势进行准确建模，从而求得当前时刻的最优对策，而超视距空战决策周期长，且态势难以用数学公式准确描述，因此并不适用。文献[6]提出多目标优化结合强化学习的方法，先通过多目标优化得到可行集，再通过强化学习寻找最优解。辛辛那提大学提出遗传模糊树[7]，开发了ALPHA空战机器人，并击败了人类飞行员，是空战决策领域最具代表性的成果之一。近年来，随着人工智能浪潮的兴起，越来越多的研究人员开始探索强化学习在空战决策问题上的应用[8-14]。尤其是DARPA在2020年举办的“阿尔法”空中格斗竞赛[15]，基于强化学习的空战智能体大比分战胜了人类飞行员，展示了智能空战的巨大研究潜力。

以上研究推动了空战决策的自动化和智能化，目前关于近距格斗的研究比较成熟，相对而言，关于超视距空战智能决策的研究并不充分，超视距空战决策的研究难度主要体现在3个方面：一是现有研究对空战态势的描述大多还是基于优势函数，如角度优势函数、距离优势函数、能量优势函数等，此类函数无法准确描述超视距空战的态势；二是两者的核心问题不同，近距空战要求在短时间内抢占发射位置，对瞬时大机动的能力要求较高，而超视距空战更关注“机动时机”问题，根据双方相对距离等态势要素决策何时开始机动、机动多长时间、何时发射导弹以及如何规避导弹等问题；三是相比于近距空战，超视距空战决策周期长、决策边界不清晰，这使强化学习方法很难训练出可解释和可接受的超视距空战智能体。

而现代空战最主要的形态是超视距空战，因此当前急需研究高效、合理的超视距空战决策方法。本文针对超视距空战机动决策问题，提出基于战术机动组合的规划方法，引入层次任务网络(hierarchical task network, HTN)，并通过多目标优化算法对其进行参数优化，仿真结果表明该方法能够输出高效的超视距空战战术执行序列。

1 超视距空战机动描述

空战战术机动动作复杂多样，很难一一列举，但复杂的战术动作可以由基础的机动动作组合而成。目前常见的机动动作有两种划分方式，依据操作方式进行划分的操作机动动作[16-17]和依据战术动作理论进行划分的战术机动动作[18]。美国NASA研究人员将机动动作划分为7类基本操纵机动[19]，分别为：最大加速，最大减速，最大过载爬升，最大过载俯冲，最大过载左转，最大过载右转及稳定飞行。这7种基础动作是从飞行员的角度，根据操作控制变量来进行划分。从战术效果角度，可以将7类基本动作进行初步的组合实现、归类细化，得到常用的6种基本的战术机动动作[19]，如图1所示。

图1 6种战术机动示意图

其中，侧转和蛇形机动是在水平面的机动，桶滚可以看作是蛇形机动同时进行垂直面的机动，俯冲、斤斗、半斤斗是在垂直面上的机动，而斤斗和半斤斗多用于近距空战，本文暂不考虑。因此，超视距空战机动可以分为两类：“侧转+垂直面机动”“蛇形+垂直面机动”。本文用参数化语言来描述这两类机动[20]，侧转机动为一个四元组φ，η，γ，h，其中为转弯角度(°)，η为过载(g)，γ为坡度(°)，h为降高(m)，表示载机在进行侧转机动的同时完成高度差为h的垂直面机动；类似地，蛇形机动为一个六元组i，t，φ，η，γ，h，其中i表示蛇形机动中的转弯次数，t表示每次转弯的时间间隔。当机动参数被指定后，完成此次机动所需要的时间也就确定了。如，侧转机动180，4，60，2 000和蛇形机动2,5,120,4,60,2 000,分别如图2(a)、(b)所示。

图2 2种战术机动示意图

通过以上2种类型的机动组合，就可以实现各种复杂的超视距空战战术。

2 基于HTN的战术机动组合模型

2.1 层次任务网络规划

HTN规划的思想与专家求解问题的思维方式十分相似，因而受到广泛的推崇。HTN规划的基本思想是利用相关领域专业知识，结合专家在实际过程中的相关经验，递归地将复杂的任务网络顺序分解，逐层细化，直到分解成为一个个可以直接独立执行的原子任务为止[21]。以系统给定的初始状态、领域知识、任务目标作为输入，输出完整的、可执行的动作方案。初始状态主要是系统在规划前初始时刻的状态信息；领域知识即指规划域，包括操作集合和方法集合，操作集合主要描述执行动作的前提条件和效果，方法集合是描述任务分解的途径和相关要求；任务目标是任务网络的起点，也是任务分解后进行执行的总目标。动作方案主要是一系列动作，构成了问题的规划解。HTN规划在任务的表达和分解、任务分派、任务完成上优势比较突出，对任务分解和细化比较符合作战人员的思维模式，利用HTN算法及其思想来对军事问题进行规划、求解和执行更容易被理解和接受。

HTN规划中最关键的部分就是方法集合，以“处方”的形式告诉系统如何对任务进行分解。

2.2 空战HTN模型

HTN规划中的主要元素包括任务、方法和操作。其中，任务表示可分解的任务；操作表示不可分解的原子任务，在本文中为单次机动；方法包括条件和分解方法，具体描述了在何种态势下如何完成任务，是HTN规划的关键。在空战HTN规划中，“任务”即要执行何种战术，“操作”即单个战术机动，多个战术机动组合完成一个战术，“方法”表示在何种态势下如何建立空战HTN网络。

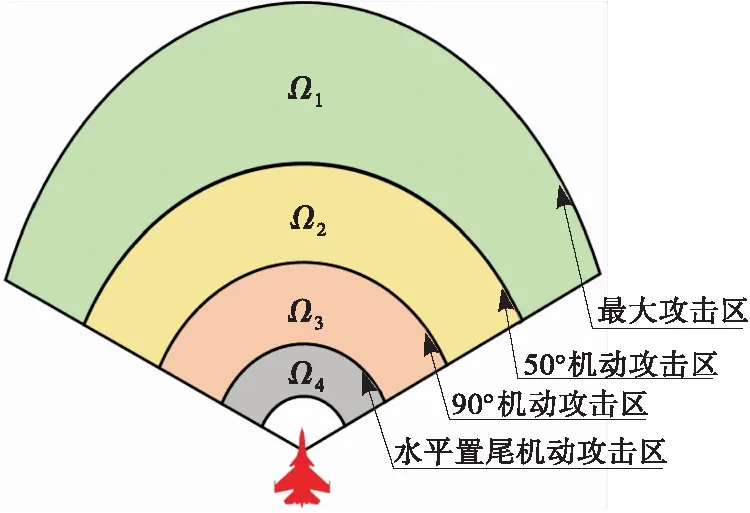
图3 攻击区划分示意图

在超视距空战中，相对距离和攻击区的关系是进行决策的重要依据。文献[22]提出基于目标机机动的五线攻击区，如图3所示，本文在此基础之上，从以下3个方面描述空战态势：①敌我相对距离与敌机攻击区的关系；②双方的相对航向；③敌机是否发射导弹。

若某种态势下需要执行“侧转+侧转+蛇形机动”的战术组合，则HTN规划见图4。

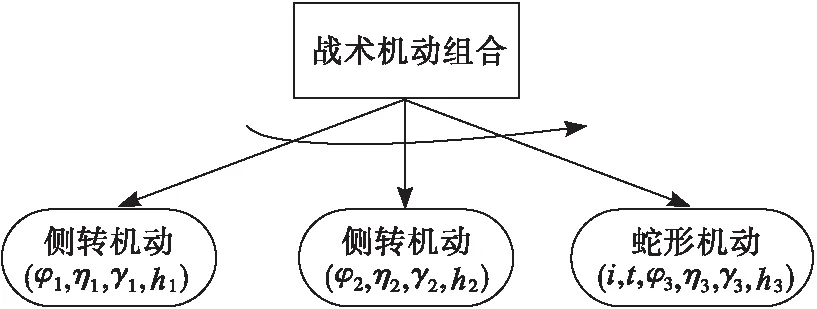
图4 空战战术机动HTN规划示意图

3 GA-HTN参数优化算法

3.1 优化模型

HTN规划确定了空战机动的顺序，但与一般HTN规划中的操作不同，空战机动由参数确定，且机动和机动之间有一定时间间隔，如图5所示，仿真开始后在t1时刻进行机动1，机动1完成后间隔t2进行机动2，之后间隔t3进行机动3。

图5 规划参数序列示意图

在机动参数给定的情况下，影响空战结果的主要是时间参数，需要通过算法进行寻优，优化目标为：①机动时间间隔之和最小；②达成发射条件的时间最长；③达成发射条件的平均距离最小。优化模型为：

(1)

式(1)是一个多目标优化问题，多目标优化问题会得到一系列帕累托最优解，不符合空战辅助决策的需求，因此将公式(1)中3个优化目标归一化后转换为单目标问题，如公式(2)：

(2)

3.2 MFO-HTN算法流程

3.2.1 MFO算法原理及流程

飞蛾扑火优化算法[23](moth-flame optimization algorithm, MFO)是一种新型智能优化算法，具有调节参数少、收敛快、不易陷入局部最优等优点。MFO算法的思想源于飞蛾沿等角螺旋路径朝火焰飞行的现象[23]，飞蛾是在搜索空间内移动的个体，火焰表示某一只飞蛾当前看到的最优解。在飞蛾朝向火焰飞行的过程中，如果发现了更好的火焰，则更新火焰的位置。算法规定一只飞蛾对应一个火焰，因此能够避免陷入局部最优。

本文中，M为飞蛾矩阵，OM为飞蛾适应度值矩阵，F为火焰位置矩阵，OF为火焰适应度值矩阵，分别如式(3)和(4)所示。

(3)

(4)

式中:n为飞蛾的个数;d为待求变量的个数。

根据适应度值对火焰位置从小到大进行排序，飞蛾分别围绕排序后的火焰，根据式(5)进行等角螺线飞行。

Mi=Diebtcos(2πt)+Fj

(5)

式中：Mi为第i只飞蛾的位置，Di=|Mi-Fj|表示第i只飞蛾与第j个火焰的距离;b为等角螺线参数;t为路径系数。

为提高算法的搜索效率，MFO采用火焰自适应减少机制，舍掉一些较差的火焰，使得飞蛾不用在劣解附近继续寻优，加快收敛速度。火焰数量自适应减少公式为:

(6)

式中：NF为当前火焰数量;N为最大火焰数量;i为当前迭代次数，I为最大迭代次数。

MFO算法流程[24]如下。

步骤1 飞蛾种群初始化。设置飞蛾数量、最大迭代次数、求解问题维度等参数。

步骤2 飞蛾位置初始化。在搜索空间中随机生成飞蛾位置，令迭代次数i=1。

步骤3 将飞蛾位置按适应度值从小到大排序后赋给火焰，作为第1代火焰的位置。

步骤4 更新飞蛾位置，将飞蛾位置适应度和火焰适应度重新排序，更新火焰位置。

步骤5 自适应减少火焰数量，迭代次数i=i+1。

步骤6 判断是否达到最大迭代次数，是则输出最优火焰位置，否则转步骤4。

3.2.2 MFO-HTN算法流程

适应度是用来度量种群中个体优劣的指标，适应度函数的设定决定算法的收敛程度和目标函数最优解。将优化目标转化为适应度函数为：

(7)

其中δ为正值常数，确保适应度函数值为正。

MFO-HTN规划流程如图6所示。

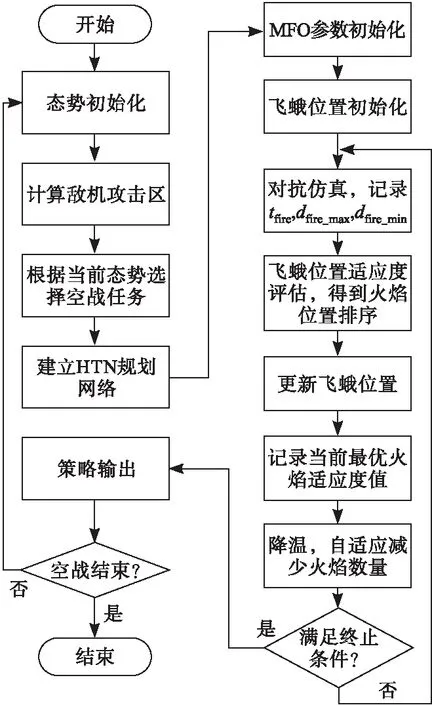
图6 MFO-HTN超视距空战规划流程图

4 仿真实验

4.1 仿真条件设置

仿真的初始态势参数包括相对距离、相对方位、相对航向角、双机的高度和速度，本节的算例设置如表1所示。

表1 初始态势参数

设敌机在0时刻发射一枚导弹，则当前空战态势满足以下描述：① 我机处于敌机的Ω3区域中；②双方为正迎头态势；③ 敌机发射一枚导弹。此时空战HTN规划网络如图7所示。

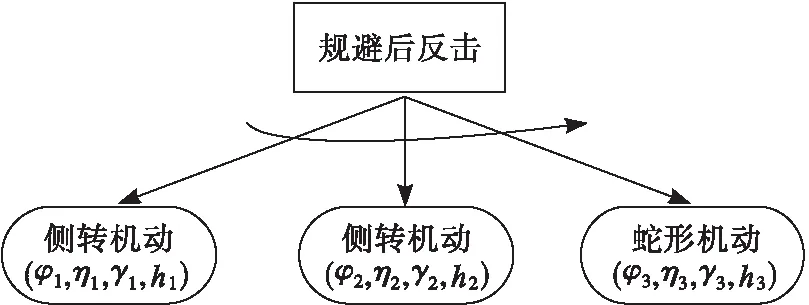
图7 空战HTN规划网络

相应的机动参数设置如表2所示。

表2 机动参数设置

4.2 飞蛾赴火算法优化结果

将本文方法与传统的遗传算法(GA)、粒子群算法(PSO)进行对比，图8展示了3种算法的收敛曲线对比。为了加快收敛速度，使算法满足实时性要求，本文限制了算法仅搜索整数解。

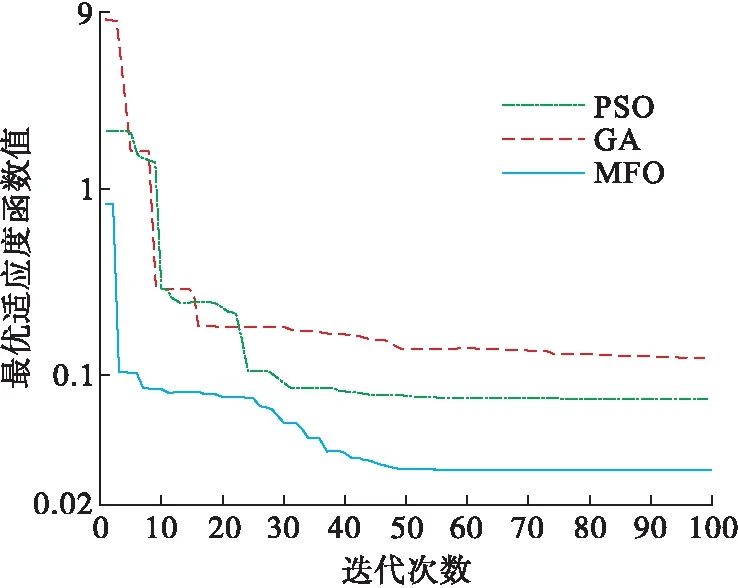
图8 算法对比

由图8可以看出，3种算法均在第50代就基本达到收敛状态，但GA和PSO算法收敛到了局部最优，MFO算法搜索精度更高，且收敛速度更快。MFO算法搜索到最优解为t1=5 s,t2=1 s,t3=4 s。

则最终得到的空战机动执行序列如图9所示。

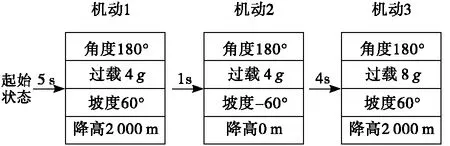
图9 空战机动执行序列

4.3 空战仿真结果

设仿真起始时刻为0时刻，整个空战仿真过程持续114 s，可分为3个阶段,见图10～12。

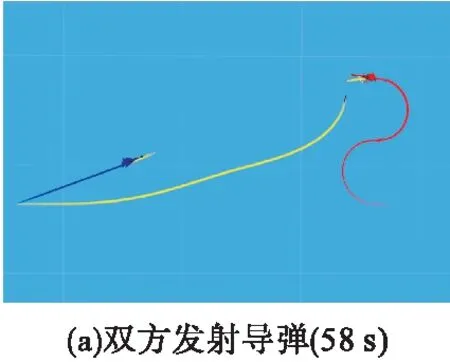
1)阶段1。敌机在0时刻发射一枚导弹，我机在5 s开始采取侧转180°机动来规避敌方导弹，同时敌机采取偏置机动保持对我机的压迫，见图10。

2)阶段2 。我机完成导弹规避后立刻形成了对敌机的锁定并发射一枚导弹，而敌机也同时发射了第2枚导弹。我机保持对敌机的锁定4 s后完成中末制导交接，导弹导引头开机，进行最后一次侧转180°机动，见图11。

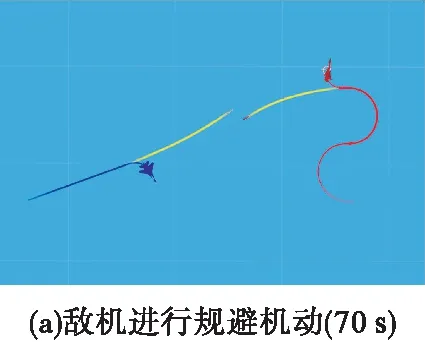
3)阶段3。70 s时，敌机向下做侧转机动规避我机发射的导弹，但在107 s时被击落，而我机随后在114 s 时完成了对敌机第2枚导弹的规避，仿真结束，见图12。

5 结语

本文提出的MFO-HTN超视距空战机动规划模型在引入专家经验的基础上，建立多目标优化模型，采用飞蛾扑火优化算法对空战HTN模型参数进行优化，能够输出高效、可解释的超视距空战战术机动执行序列。研究成果可以为飞行员提供辅助决策，也为研究智能超视距空战提供了新的思路。下一步研究如何将HTN模型与模糊推理、强化学习等算法相结合，构建更灵活、可扩展的超视距空战战术模型。