“等时圆”对折射定律的表示意义

黄 伟 陈 珂

（1.湖北汉川一中，湖北 孝感 431600；2.武汉光谷教育发展研究院，湖北 武汉 430000）

折射定律概括了光线在不同光介质中传播的基本规律.折射定律是几何光学的基本原理，它的发现奠定了几何光学的定量地位.折射定律有3种表示方式，分别是斯涅耳原理、费马原理、惠更斯原理.

1 折射定律的发展及深入理解

公元2世纪，古希腊人托勒密（约90—168）通过实验研究了光的折射现象，并得出“折射角与入射角成正比”的结论.1611年，德国科学家开普勒（1571—1630）在其系统研究的基础上，写成了《折射光》一书，指出托勒密的折射定律只适用于入射角小于30°的情况.他认为折射角是由两部分组成的，一部分正比于入射角，另一部分正比于入射角的正割，对折射定律的研究开普勒比托勒密前进了一步，但他没找到折射定律的正确形式.

1.1 斯涅耳的折射定律

折射定律物理上的正确表述最早是由荷兰数学家斯涅耳（1591—1626）于1621年由实验得出，他作了这样的表述：对于给定的两种介质，入射角和折射角的余割之比总是保持相同的值.他研究了水中的物体看起来像漂浮的现象，如图1所示，当从空气中的A点观察水中的B点时，犹如在E点一样.斯涅耳发现：对于任意入射角，存在以下关系

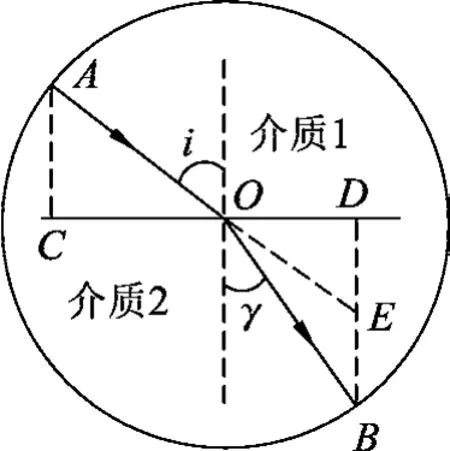
图1

斯涅耳得出这一定律，但他在世时并未公开发表，1626年，惠更斯阅读其遗稿后，才正式发表.斯涅耳的折射定律只是实验结果，没有作理论上的推导.

1.2 费马原理与折射定律

费马原理为折射定律提供了严格准确的证明.

法国数学家费马（1601～1665）在1662年提出：光传播的路径是光程取极值的路径.“取极值”在数学上可理解为一阶导数为0，它可以是极大值、极小值甚至是拐点.用光程表示的费马原理为

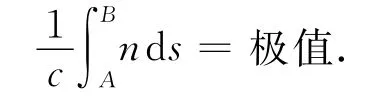
参考图1，若光从A点出射通过分界面到达B点，设介质1中光速为v1，介质2中光速为v2，令AC=a，BD=b，CD=l，CO=x，则通过的时间为

费马原理还可表述为：在所有可能的光传播途径中，实际路径所需的时间取极值.

1.3 惠更斯原理与折射定律

惠更斯原理从光的波动说的角度更加形象地解释了折射定律.

荷兰物理学家惠更斯（1629—1695）在1690年出版的《光论》一书中正式提出了光的波动说，建立了著名的惠更斯原理（后发展为“惠更斯-菲涅耳原理”）.在此原理基础上，他推导出了光的反射和折射定律，圆满地解释了光速在光密介质中减小的原因.

惠更斯原理指出：介质中任一波面上的各点，都可以看作发射子波的波源，其后任意时刻，这些子波在波前进方向的包络面就是新的波面.如图2所示，由惠更斯原理，O、B为同一波面上的两点，经Δt后，O点发射的子波到达界面处A点，B点发射的子波到达C点，由于

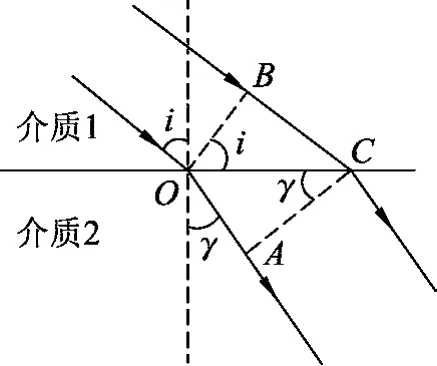
图2

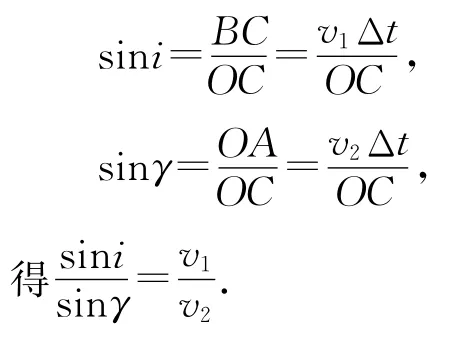
2 惠更斯原理下“等时圆”的几何表示

惠更斯用波前的概念表示光波的传播，如图2是惠更斯原理的几何三角形的表示，三角形表示的意义在于直观呈现在不同介质中，光线行进方向的转向关系.几何三角形还可以被“等时圆”的形式等价表示，“等时圆”表示的意义在于直观呈现不同折射率光线相同时间的光程大小关系.

2.1 惠更斯“等时圆”模型

如图3所示，一束白光从真空射入某种介质中，发生折射后，各种单色光到达以入射点O为端点、界面为直径的一个几何圆周上的时间相等，与折射率无关.

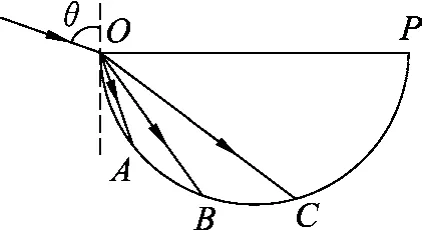
图3

证明：如图4所示，OB为其中一束折射光线，设入射角为θ，折射角为α，圆的半径为R，则此束光线在介质中从O传到B的时间

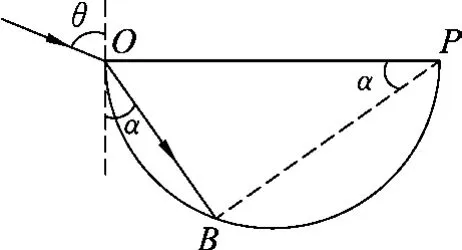
图4

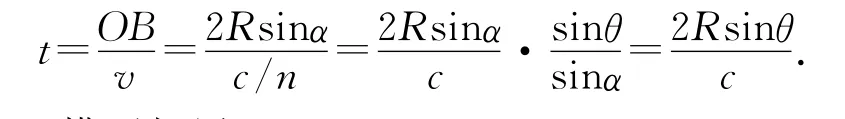
2.2 模型拓展

复色光从真空射入平行透明砖色散的两个推论.

推论1：折射角为45°的折射光通过平行透明砖时间最短.

证明：如图5所示，以入射点O为端点，上界面为直径作圆，与下界面相切于B点，由惠更斯“等时圆”可知，折射光线OB在介质中传播时间最短，此时折射角为45°.

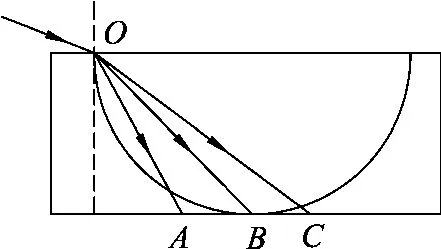
图5

推论2：折射角互余（关于折射角为45°折射光线角对称）的两束折射光通过平行透明砖时间相等.

证明：如图6所示，由惠更斯“等时圆”可知，折射光线OA、OC在介质中传播的时间相等，由圆的几何对称关系可得，其折射角∠POA与∠POC互余，即关于折射角为45°折射光线角对称.

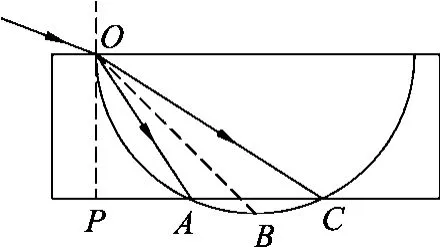
图6

2.3 模型应用

例1.（2008年全国卷Ⅰ第21题改编）如图7所示，一束由红、蓝两单色光组成的光线从一平行透明砖上表面以入射角θ射入，穿过平行透明砖自下表面射出，则在θ从0°逐渐增大至90°的过程中，求哪种色光先射出透明砖（设平行透明砖厚度为d，对红光折射率为n1，对蓝光折射率为n2）.

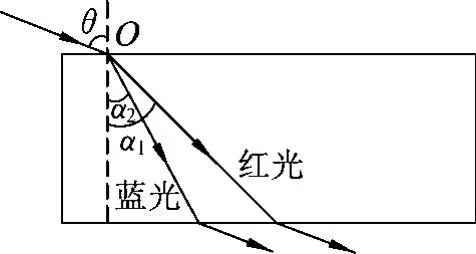
图7

解析：（1）用折射定律求解.

设红光与蓝光穿过砖所用时间为t1和t2，根据路程，折射率，速度，可得时间，原高考题中n=1.5，进1一步计算可得t1＜t2.

这类题目一般以选择题的形式出现，利用折射定律求解计算量较大，若介质折射率未知则需分类讨论，更为复杂.

（2）“等时圆”图解很直观.

例1中，当入射角为θ=90°、折射角为α=45°时，

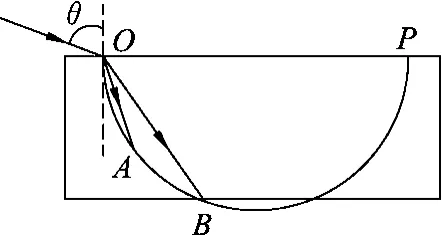
图8

（a）当入射角为临界角θ0时，如图9所示，红光、蓝光同时射出透明砖.

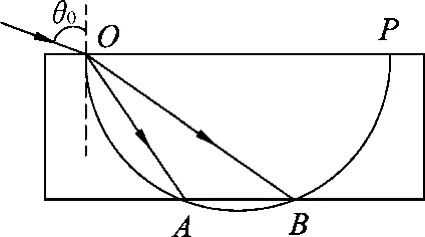
图9

（b）当入射角小于临界角θ0时，如图8所示，红光先射出透明砖.

（c）当入射角大于临界角θ0时，如图10所示，蓝光先射出透明砖.

图10

例2.如图11所示，某玻璃砖的横截面是等腰直角三角形，一束由红蓝两色组成的复色光从AB边的O点平行于BC边射入后，两种色光均在BC发生全反射后首次从AC边射出玻璃砖，求哪种色光先射出透明砖.

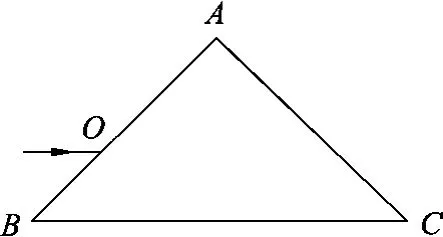
图11

解析：“等时圆”图解.如图12所示，构建正方形平行玻璃砖ABDC，由几何对称关系可知，红光由O传到E与O传到E′的时间相等，蓝光由O传到F与O传到F′的时间相等，由上述平行透明砖的推论可知，红光先射出玻璃砖.

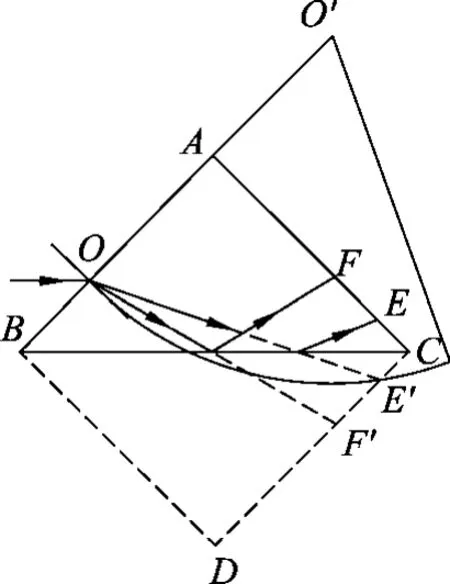
图12

3 结束语

综上所述，利用惠更斯“等时圆”比较光通过平行玻璃砖的时间非常形象直观，“等时圆”表示折射定律使其物理意义得以更加明确地体现.在教学中，加强“物理模型”的构建与转化应用，有利于培养学生的科学思维、发展学生物理学科核心素养.